商近似空间中粗糙集的研究

赵焕敏 马利文

(北京邮电大学理学院，北京 100876)

0 引 言

覆盖粗糙集理论作为Pawlak经典粗糙集理论的一种推广，在解决智能系统中的许多复杂问题方面得到应用，有丰富的理论价值．越来越多的学者从不同的角度来研究粗糙集理论(如文献[1-11])．在Pawlak经典粗糙集理论和其他广义粗糙集理论中，研究的核心内容是空间中粗糙子集的上下近似，所以很多文献中，定义和研究了覆盖近似空间上各种不同的上下近似算子．本文从新的思路出发，基于覆盖近似空间上的一种等价关系，定义了一种新的近似空间：覆盖近似空间的商近似空间．通过给定源空间中元素的邻域和余邻域的概念，定义了所研究商近似空间上的2对上下近似算子，并详细介绍其具有的良好性质，结合文献[12]中对商空间性质的保持性的证明，给出一些例子作理解，为进一步解决实际问题提供新的方法和理论支撑．

1 基础概念

本节简单介绍覆盖粗糙集理论中的一些基础概念及相关性质．

定义1[10]设U是一个有限集合，C是由U的非空子集构成的集族且U=∪C∈CC，则称集族C是集合U的一个覆盖，且称有序对(U，C)是一个覆盖近似空间．

设U是全集，对于U的每一个子集X，用-X表示它的余集．

定义2[2,9-10]设(U，C)是一个覆盖近似空间．对于任一x∈U，称

N(x)=∩{C∈C：x∈C},M(x)=-(∪{C∈C：x∉C})

分别为元素x的邻域和余邻域．

明显地，余邻域的定义还可以表示为M(x)=∩{-C：(C∈C)∧(x∉C)}．若对于任一C∈C，有x∈C，则规定M(x)=U．

定义3[3]设(U，C)是一个覆盖近似空间，A⊂U，称

N(A)=∪{N(x)：x∈A},M(A)=∪{M(x)：x∈A}

分别为集合A的邻域和余邻域．

命题1[2]设(U，C)是一个覆盖近似空间，x,y∈U，则y∈N(x)当且仅当x∈M(y)．

命题2[2,10]设(U，C)是一个覆盖近似空间，则对于每一C∈C，有

命题3[2]邻域算子N和余邻域算子M都满足传递性，即若x∈N(y)且y∈N(z)，则x∈N(z)；若x∈M(y)且y∈M(z)，则x∈M(z)．

定义4[2]对于覆盖近似空间(U，C)的每一个子集A，定义A的下近似和上近似分别为：

命题4设(U，C)是一个覆盖近似空间，则对于每一C∈C，有

2 商近似空间上的粗糙集

本节定义了1个覆盖近似空间上的商近似空间和此商近似空间中子集的2对上下近似．

定义5设(U，C)是1个覆盖近似空间，R是U中的1个等价关系，则W=U/R是U在等价关系R下的1个商空间．令F={F⊂W：R-1(F)=N(R-1(F))}，即集族F由商空间中原像是源空间中的邻域或邻域的并的集合构成．容易验证，F是W的1个覆盖，称(W，F)是源空间(U，C)在等价关系R下的商近似空间．

例1令U={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10}，记C1={x1,x4}，C2={x2,x3}，C3={x1,x2,x3}，C4={x4,x5,x6,x7}，C5={x6,x7,x8,x9}，C6={x4,x5,x6,x7,x10}，则C={C1,C2,C3,C4,C5,C6}是U的1个覆盖．对于覆盖近似空间(U，C)，若等价关系R诱导U上的一个划分为y1={x1}，y2={x2,x3,x4,x5}，y3={x6,x7}，y4={x8,x9}，y5={x10}，则对于W=U/R={y1,y2,y3,y4,y5}，通过对元素邻域的计算，得到F1={y1}，F2={y2,y3}，F3={y3}，F4={y3,y4}，F5={y2,y3,y5}，则F={F1,F2,F3,F4,F5}是W的1个覆盖且(W，F)是源空间(U，C)的商近似空间．

定义6若(W，F)是源空间(U，C)的商近似空间，则对于任一y∈W，称

n(y)=∩{F∈F：y∈F},m(y)=∩{-F：(F∈F)∧(y∉F)}

分别为元素y的商邻域和商余邻域．对于任一子集Y⊂W，称

n(Y)=∪{n(y)：y∈Y},m(Y)=∪{m(y)：y∈Y}

分别为集合Y的商邻域和商余邻域．

例2考虑例1的源空间和商近似空间，取Y={y2,y3}，通过计算得到n(Y)={y2,y3},m(Y)={y2,y3,y4,y5}．

容易验证，在下列性质方面，商近似算子n、m与近似算子N、M相同．

命题5设(W，F)是源空间(U，C)的商近似空间，则商邻域算子n和商余邻域算子m都满足传递性，且对于任意y,z∈W,y∈n(z),当且仅当z∈m(y)．

命题6设(W，F)是源空间(U，C)的商近似空间，则对于任一F∈F，有F=n(F),-F=m(-F),R-1(-F)=M(R-1(-F))．

证明假设F∈F，n(F)=∪{n(y)：y∈F}，由双包含关系得到F=n(F)，对于第2个等式，很明显，左包含-F⊆∪{m(y)：y∈-F}成立，且对于任一y∈-F，有m(y)⊆-F成立，所以∪{m(y)：y∈-F}⊆-F，故-F=∪{m(y)：y∈-F}．

对于第3个等式，容易验证，R-1(-F)⊆∪{M(x)：x∈R-1(-F)}，只需要证明R-1(-F)⊇∪{M(x)：x∈R-1(-F)}．若x∈R-1(-F)=-R-1(F)且M(x)R-1(-F)，则存在元素z∈M(x)且z∉R-1(-F)=-R-1(F)，所以z∈R-1(F)并N(z)⊆R-1(F)．根据命题1，对任意x,y∈U，y∈N(x)当且仅当x∈M(y)，得到x∈N(z)，所以x∈R-1(F)，这与x∈R-1(-F)=-R-1(F)矛盾．这证明对任一x∈R-1(-F)，有M(x)⊆R-1(-F)，故R-1(-F)⊇∪{M(x)：x∈R-1(-F)}．

下面定义商近似空间中子集的上下近似．

定义7设(W，F)是源空间(U，C)的商近似空间且Y⊂W，定义子集Y的2对下近似和上近似分别为：

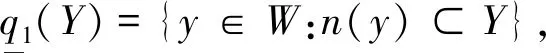
例3考虑例1的源空间和商近似空间，取Y1={y1,y2},Y2={y2,y3,y4}，通过计算得到:

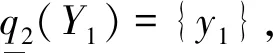
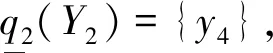
3 商近似空间中近似算子的性质

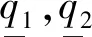
由定义5和命题6，容易验证命题8．

命题8设(W，F)是源空间(U，C)的商近似空间，则对于任一F∈F，有：

基于此，命题9可以直接得到．

命题9设(W，F)是源空间(U，C)的商近似空间，则对于任一F∈F，有：

下面讨论商邻域和商余邻域在等价关系R下逆像的性质．

命题10设(W，F)是源空间(U，C)在等价关系R下的商近似空间，则对于任一y∈W，有：

(1)R-1(n(y))=N(R-1(n(y)));

(2)R-1(m(y))=M(R-1(m(y))).

证明根据定义6和命题6，可以得到：

N(R-1(n(y)));

接下来，研究近似集在等价关系R下像和逆像的性质．

命题11设(W，F)是源空间(U，C)在等价关系R下的商近似空间，则有：

(1)对于任一

同理，可以证得对于任一

举1个例子说明上述性质中的等号不成立．

令Y1={y3},Y2={y5},Y3=Y4={y2}，则

R-1(Y1)={x6,x7},R-1(Y2)={x10},R-1(Y3)=R-1(Y4)={x2,x3,x4,x5}．

且下列各式成立：

4 结论和讨论

在大数据分析和应用中需对数据集进行分类，把所有类作为新的元素进行研究，这便是商空间．不仅减少了研究对象的数量，而且由于每类元素整体作为一个对象，使其共性得以保留，这点在文献[12]中也被详细证明．本文定义了1个覆盖近似空间上的商近似空间，基于邻域和余邻域的概念对此商近似空间作出相关性质的证明和研究．由于邻域和余邻域是近似空间中的点的基本描述元，代表点的性质的基本单位，因而命题10充分说明了商近似空间很好地保留了源空间的邻域与余邻域所代表的性质．这也是商空间理论的初衷，对后面应用新定义的商近似空间模型解决属性约简、决策规则发现等实际问题提供了重要理论基础．事实上，对覆盖近似空间(U，C)的商空间W=U/R， 自然想到定义其覆盖为G={R(C)：C∈C}，文献[11]通过探究映射f所满足的条件，对得到的映射空间做了初步分析.但由这样定义覆盖得到的邻域{n(y)：y∈W}与余邻域{m(y)：y∈W}不具有本文定义的商近似空间所具有的命题10．读者可以利用例1的数据自行检验这一点．这便是本文所定义的商近似空间的优越性所在．

命题11表明本文所定义的商近似空间中的上下近似与源空间的上下近似有一种确定的重要的关系，此性质也是上述覆盖G定义法不能具备的．这一点对算子的应用是非常有益的，使得其上下近似的变化能被很好的把握，是放大还是缩小，对结合实例进一步研究粗糙集提供了重要启示．