AlN超声换能器声场的仿真分析

陈继明，马希直，李响

(南京航空航天大学 机电学院，江苏 南京 210016)

1 不同介质中的声传播理论

声压p、质点速度u和媒介密度变化量ρ'是声场中的3个最基本的物理量[1]。在小振幅情况下，进行线性化近似，它们之间的关系可通过下述3个物理定律进行描述：

声压p与质点速度u之间的关系可通过运动方程(牛顿第二定律)来表示：

(1)

质点速度u和媒介密度变化量ρ'之间的关系可通过连续性方程(质量守恒定律)来表示：

(2)

声压p和媒介密度变化量ρ'之间的关系可通过物态方程(热力学定律)来表示：

p=c2ρ′

(3)

其中c为声波传播的速度。

由于流体与固体介质在结构与性质上有着明显的差异，因此，描述它们中声波传播的基本波形及波动方程也不同[2]。

1.1 流体中的波动方程

假设流体无损耗且绝热，忽略黏性效应，并使用线性等熵状态方程，对式(1)-式(3)进行处理，消去u和ρ'可以推导出波动方程：

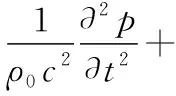
(4)

利用下面的数学关系：

div(gradp)=·(p)=2p

(5)

利用式(5)对式(4)进行化简得到波动方程：

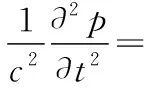
(6)

声学问题经常包括简单的简谐波，比如正弦波。一般情况下，任何信号都可以由傅里叶变换转换为一系列谐波成分，波动方程可以在频域上一次求解一个频率。谐波一般形式如下：

p(x,t)=p(x)sin(ωt)

其中空间项p(x)和时间项sin(ωt)是分离的[3]。为了运算的方便，压力可以更广义地写成复数变量：

p(x,t)=p(x)eiωt

(7)

实际声压的(瞬时)物理值是式(7)的实数部分[4]。对声压做上述假设后，将式(7)代入式(6)，瞬态的波动方程就变成了Helmholtz方程：

2p(x)+k2p(x)=0

(8)

1.2 流体中的平面波

(9)

对式(9)进行求解，可以得到沿x轴方向传播的平面波：

p(x,t)=P0ei(ωt-kx)

(10)

将式(10)代入式(1)运动方程中，可以得到质点的速度为

u(x,t)=u0ei(ωt-kx)

(11)

其中：P0=jωρ0A表示波的振幅；u0=jkA表示质点速度幅值；A表征传播过程中振幅的任意量。可以看出平面波的声压和质点速度是同相的。同时，可以得到平面波的声阻抗率Zs=p/u=ρ0c0，其中ρ0、c0分别为声介质的密度和声速[5]。

1.3 固体中的波动方程

固体与流体不同，除了体积弹性之外，它们还具有剪切弹性。流体不可避免有静压力，作为逾量压强的声压是个标量，其波动方程也采用标量形式，而固体中没有静压力，但其中的应力、应变和弹性需要用矢量和张量表示，数学上较为复杂[6]。

对于各向同性的理想弹性固体，根据其力矩平衡条件和弹性常数的对称性，已经证明，其独立的弹性常数只有两个，即梅拉常数λ'和μ'，与其杨氏模量E，泊松比σ、体积弹性模量B有下述关系：

(12)

反过来，用E、σ表示λ'和μ'公式为：

(13)

利用这两个独立的弹性常数，结合牛顿第二定律及广义胡克定律可得到固体中的波动方程：

(14)

或

(15)

其中ξ为质点振动位移矢量，且有：

1.4 固体中的压缩波

由波动方程式(14)可以看出，在等号右边有两个与空间变化有关的项。第一项含有位移矢量的散度·ξ，第二项含有位移矢量的旋度×ξ。作为第一种情况，设ξ为无旋矢量，即×ξ=0，此时波动方程为：

(16)

式(16)是固体中压缩波的波动方程。它与流体中的波动方程具有相同的形式，只是声速用固体中压缩波的声速表达式而已[7]。由此可知，与流体中的情况相对应，固体中的压缩波也应存在平面、球面及柱面3种基本波型。

当质点只有x方向位移时，式(16)变为

(17)

这就是沿x方向传播的平面纵波波动方程，因为式(17)的解ξx(x,t)是质点沿x方向的振动位移，与平面波传播方向一致[8]。同时表明，平面纵波的传播速度就等于压缩波的声速。

2 频域分析

2.1 建立有限元模型

频域分析中，缩小换能器的尺寸，油液尺寸相对增加，建立电-固-声耦合有限元模型如图1所示，油液区域为1/4圆，将下部换能器放大如左图所示。这部分采用声学模块下的声-压电相互作用(频域)接口进行仿真，扫频范围为10MHz～30MHz，频率间隔为0.1MHz。压力声学油域设置上边界为球面波辐射条件，不让其声波进行反射以获得超声换能器产生的原始声压的数据；固体力学域设置好不锈钢、电极材料和硅基的阻尼，另外还有不锈钢横向边界的固定约束；静电学域设置上电极边界条件为100V电压，下电极边界条件设置为接地[9]。

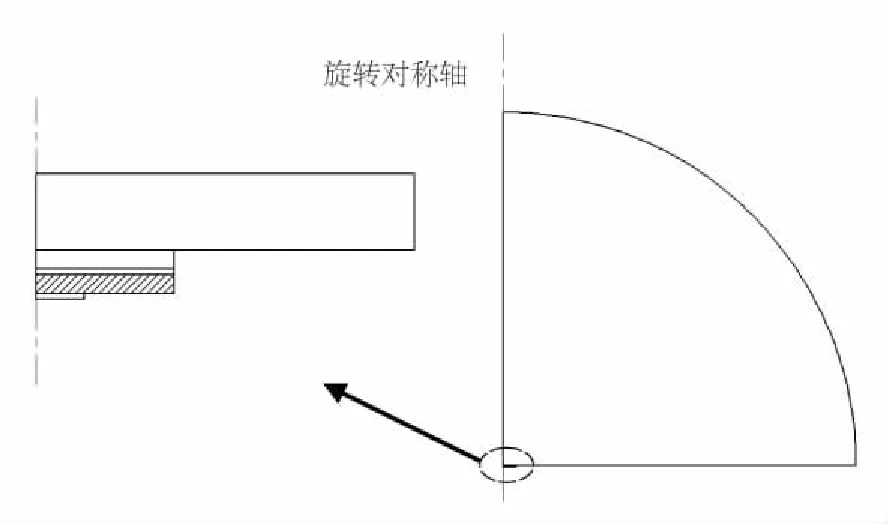
图1 有限元模型

2.2 结果分析

1) 声压分析

超声换能器的上下振动导致空气压强的变化，由此产生声压。图2是超声换能器中心点在油液中所产生的声压随频率变化的曲线，由图可以看出声压在17.6MHz时达到极大值，即在此时，超声换能器发生共振，而在其他位置，换能器只是受迫振动，所产生的声压远远小于共振点的声压。如图3 所示，声压级也在此处达到最大值。

图2 声压随频率变化曲线

图3 声压级随频率变化曲线

2) 声场分析

超声换能器的大小和无限大声场相比可以看成1个点，所以在17.6MHz的正弦波激励下，换能器产生的声波在油液中以球面波形式传播。图4和图5分别是声压场二维图和二维高度图，由图可以看出声压最大值出现在换能器表面，沿传播方向逐渐衰减，而且先衰减较快后衰减较慢。

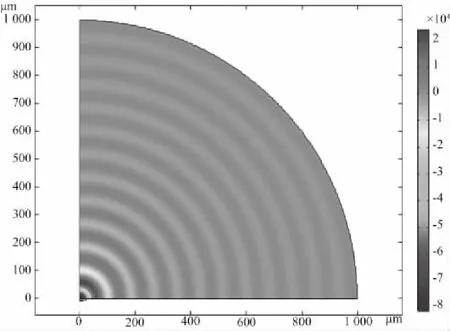
图4 共振频率处的二维声压图

图5 共振频率下的声压二维高度图

图6是共振频率下的声压级二维图，可以看出最大声压级也是出现在换能器表面，大小在195dB左右，这和图3中换能器中心点的最大声压级相符。

图6 共振频率下的声压级二维图

图7是沿超声换能器与油液交界面声压的变化曲线，由图可以看出换能器中心点声压最大，沿表面逐渐减小，这是由于换能器中心点振动幅度最大。图中心点最大声压约为160kPa，这与图2相符合。

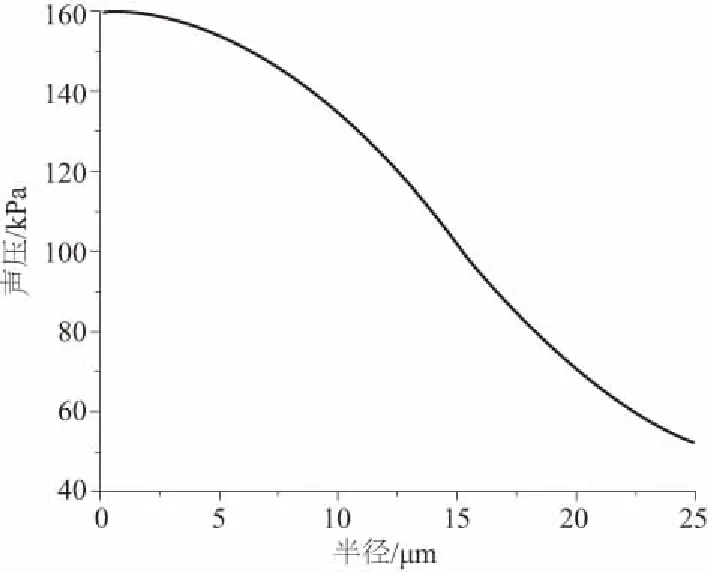
图7 声压沿换能器表面的变化曲线

3 时域分析

同样，为了节省计算时间，模型整体设置二维旋转对称，时域分析时模型采用换能器的实际尺寸，建立电-固-声耦合模型如图8所示，换能器结构与之前基本一致，中间换能器从上到下依次为不锈钢、硅片、上电极(铝)、AlN和下电极(铝)，上方长方形是油液区域。由于要验证声波在油液中的传播过程，这里油液长度设置为10个波长，方便观察和计算；下方小正方形是空气域，用于对比油液中的声波强度。

油液上边界设置为硬声场边界条件，声波在此边界上全部反射；空气域下边界设置为平面波辐射，声波在此边界上全部吸收。不锈钢右边界设置为固定约束，压电层与上电极接触面设置200V的正弦电压，压电层与下电极接触面设置接地。

图8 有限元模型

超声换能器在7.3MHz激励电压的激励下向油液中传播声波，1个周期约为0.137μs，如图9中分别对应声波传播5个周期、10个周期、15个周期和20个周期时声场的分布，由激励信号可知声场中有5个周期的声波在传播，图9中可以看出5个周期的声波在油液中传播，声波在0.69μs时全部进入油液区域，在1.37μs时到达反射界面，在2.06μs是全部反射，在2.74μs时到达换能器表面，与理论解析结果一致。

图9 不同时间的声场分布

为了模拟更加真实的情况，对不锈钢和电极材料添加了阻尼系数，对压电层添加了阻尼系数和介电损耗。图10是换能器与油液域交界面声压随时间变化曲线，前5个周期的声压和激励信号大致一致，到2.74μs左右时，声波经过反射回到换能器表面，此时声压幅值是之前的两倍，这是由于声压又在此表面发生了反射，2.74μs之后的5个周期换能器与油液交界面的声压是返回后的声压与再次反射的声压的叠加。图11是上方油液域上边界的声压随时间变化曲线，声波在1.37μs时到达反射界面，此时声压幅值也是发射声压的两倍，原因与之前一样，油域反射界面处的声压是入射声压与第1次反射声压的叠加。

图10 换能器与油液域交界面声压随时间变化曲线

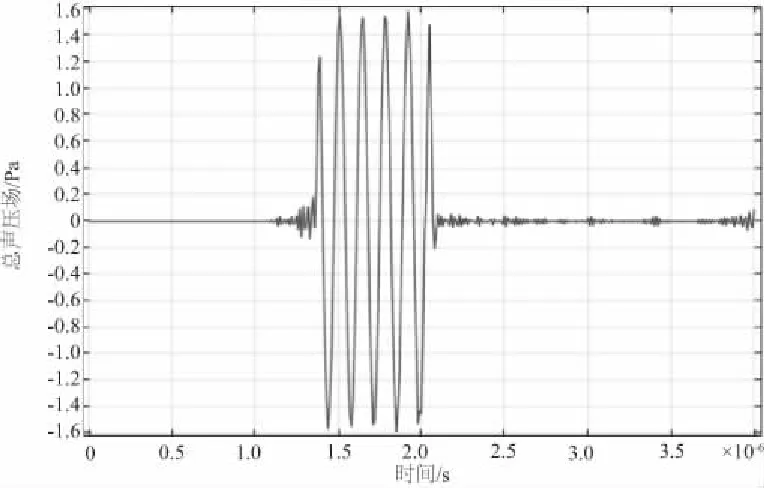
图11 油域反射界面声压随时间变化曲线

图12是换能器与空气域交界面声压随时间变化曲线，前5个周期声压与激励电压相符，但这里的声压幅值明显大于油液域的发射声压幅值，这是由于换能器被衬材料的阻尼不同所导致的。前段发射声压的被衬材料是空气或者说是没有被衬材料，而后端发射声压的被衬材料是不锈钢。不锈钢的阻尼远远大于空气的阻尼，所以换能器高频振动所产生的声压更多的是向后端空气中发射，这是不愿意看到的现象，也是此种应用的一个弊端。后期可以适当地添加更好的被衬材料来达到更加理想的效果。0.68μs之后的声压显得有点杂乱无章，这是由于设置的平面波辐射界面不是理想的无反射边界，有一定的声波反射，空气区域设置较小，声波来回反射导致的。

图12 换能器与空气域交界面声压随时间变化曲线

4 结语

本文在声学理论的基础上，描述了换能器在不同介质中声传播方程，建立了电-固-声耦合分析频域与时域模型。对AlN超声换能器整体结构进行了频域分析，求解出了其声学共振频率，并分析了共振频率下的声压、声压级。通过瞬态求解，分析了换能器在脉冲激励下的声传播过程，对声信号的发射、反射接收信号作了解析。