INFINITELY MANY SOLITARY WAVES DUE TO THE SECOND-HARMONIC GENERATION IN QUADRATIC MEDIA∗
Chunhua WANG(王春花)
School of Mathematics and Statistics and Hubei Key Laboratory Mathematical Sciences,Central China Normal University,Wuhan 430079,China
E-mail:chunhuawang@mail.ccnu.edu.cn
Jing ZHOU(周静)
School of Mathematics and Statistics and Hubei Key Laboratory Mathematical Sciences,Central China Normal University,Wuhan 430079,China
School of Mathematics and Statistics,South-Central University for Nationalities,Wuhan 430000,China
E-mail:zhouj@mail.scuec.edu.cn
Abstract In this paper,we consider the following coupled Schrödinger system with χ(2)nonlinearitieswhich arises from second-harmonic generation in quadratic media.Here V1(x)and V2(x)are radially positive functions,2 ≤ N<6,α >0 and α > β.Assume that the potential functions V1(x)and V2(x)satisfy some algebraic decay at in fi nity.Applying the finite dimensional reduction method,we construct an unbounded sequence of non-radial vector solutions of synchronized type.
Key words χ(2)nonlinearities;second-harmonic generation;synchronized solution;reduction method
1 Introduction and Main Result
In this paper,we consider the following coupled Schrödinger system with χ(2)nonlinearities
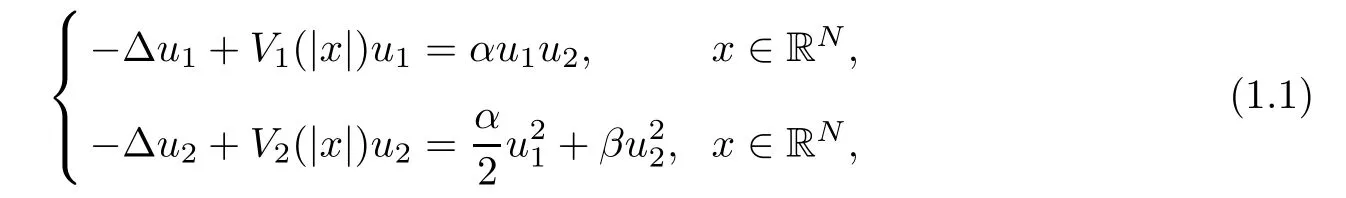
which arises from second-harmonic generation in quadratic media.Here V1(|x|)and V2(|x|)are positive potential functions,2≤ N<6,α >0 and α > β.
It is well-known that nonlinear Schrödinger(NLS)equations appear in many contexts,for example,in photonics,plasmas,foundation of quantum mechanics,optics in nonlinear media or in mean- field theory of Bose-Einstein condensates and so on.Particularly in nonlinear media optic theory,the(NLS)equation appears as an asymptotic limit for a slowly varying dispersive wave envelope propagating in nonlinear medium.The cubic nonlinear Schrödinger(NLS)equation

is the base describing the formation and propagation of different type of optical solitons in Kerr-type material[9,24].Here V is a slowly varying envelope of electric field,the realvalued parameter r and χ represent the relative strength and sign of dispersion/di ff raction and nonlinearity,respectively,and z is the propagation distance coordinate.The Laplacian operator ∇2can either be ∂2/∂τ2for temporal solitons where τ is the normalized retarded time,orwhere x=(x1,···,xN)is the spatial coordinate with the spatial dimension N≥1.Here x is in the direction orthogonal to z.Solitary wave solutions to(1.2)and its generations were proved in,for example[5,23].Similar resuts about some Schödinger equations,we can refer to[15,26].
In the mean- field approximation,the system described by the Gross-Pitaevskii equations
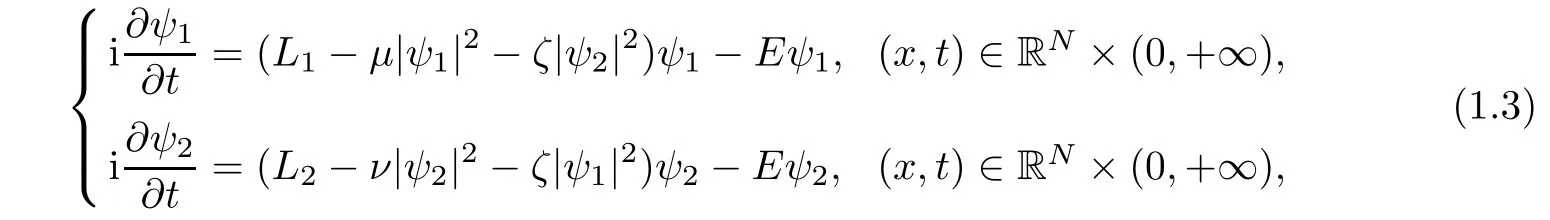
where Lj= −∇2+Vjwith j=1,2,µ,ν,ζ and E are real parameters.The model which the propagation of solitons χ(3)in nonlinear fi ber couples based on is equivalent to(1.3).Here ψj(j=1,2)denotes the j-th component of the light beam.This system received a lot of attention both experimentally and theoretically.The standing-wave solutions ψj(j=1,2),which are those of the form ψj=ujeiEtwith uja real-valued function,satisfy
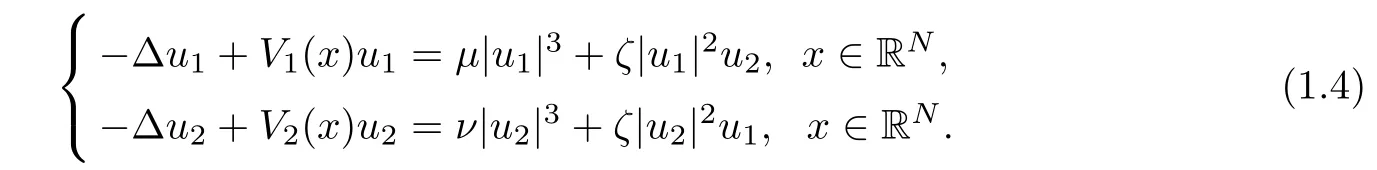
The existence of solitary waves to(1.4)was well-studied and was explored by many researchers in recent years,for example,[1–4,12,16–19,22,25,27,28].
Nonlinear optical e ff ects such as Second Harmonic Generation(SHG)were discovered when the optical material has a χ(2)(i.e.,quatratic)nonlinear optical nonlinear response instead of conventional χ(3)material for which(1.2)is based on(see[6,7]).The invention of lasers in 1960s enabled experimental physical scientists to obtain a powerful source of coherent light.It is well-known that the second-order(or quadratic)nonlinearities of optical χ(2)materials are responsible for such e ff ects as the second harmonic generation(SHG).Recent progress in materials with high second-order nonlinearities,including polymeric electro-optical waveguide,has stimulated experimental e ff orts to increase indirectly e ff ective χ(3)nonlinearities taking advantages of cascaded second-order e ff ects.Suppose that we consider a strong parametric interaction of three stationary quasi-plane monochromatic waves with frequencies ωi(i=1,2,3),there is no walk-o ffbetween harmonic waves,the frequencies of interacting waves are matched exactly(ω1+ω2= ω3),and corresponding wave vectors are almost matched(k1ω1+k2ω2− k3ω3= ∆k ≪ ki,where ki=|Ki|and Ki=Ki(ωi)are wave vectors.Then with some conventional normalizations and the assumption that ω1= ω2=,we can obtain the following system of type-I SHG(see[6],p.104)
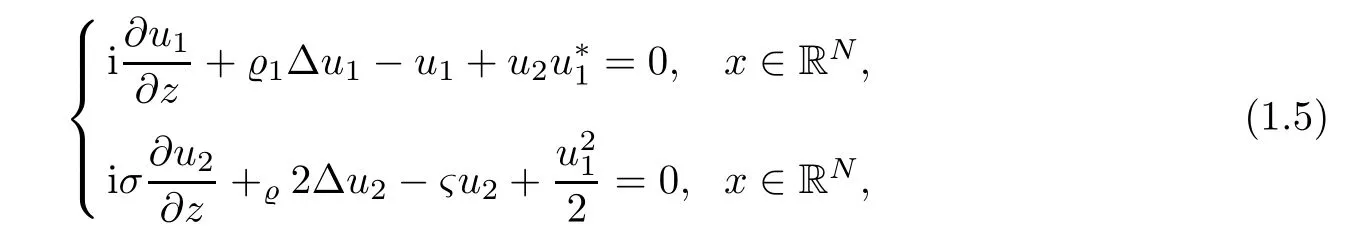
where u1is a renormalized slowly varying complex envelope of wave with frequency ω1,u1is the one with frequency ω3,σ,ς>0 and1,̺2= ±1.In the spatial soliton case1=2=1,while the temporal case all four combinations for1,̺2= ±1 are possible.The physically realistic spatial dimensions are N=1 or N=2.Then the chirp-free two-wave(symbiotic)solitons can be found as real-valued solutions of the steady state(=0)equation
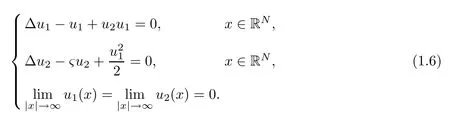
On the other hand,the type II SHG can be described by the following renormalized threewave mixing equation(see[6],p.108)

and its steady equation is of the following form
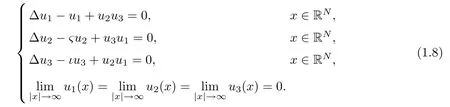
In this paper,we are only concerned with the type-I SHG.In the case N=1,the existence of a non-trivial ground state solution of(1.6)was shown in[31]by using a variational approach.Multi-pulse solutions of(1.6)for N=1 were first observed in numerical simulations(see[31]),and the existence of multi-pulse solutions was analytically proved using singular perturbation theory in[30].
By contrast with the coupled Schrödinger system with χ(3)nonlinearities,little attention is given to the the coupled Schrödinger system with χ(2)nonlinearities.Hence,we will consider a more general problem of studying the wave solutions to the problem
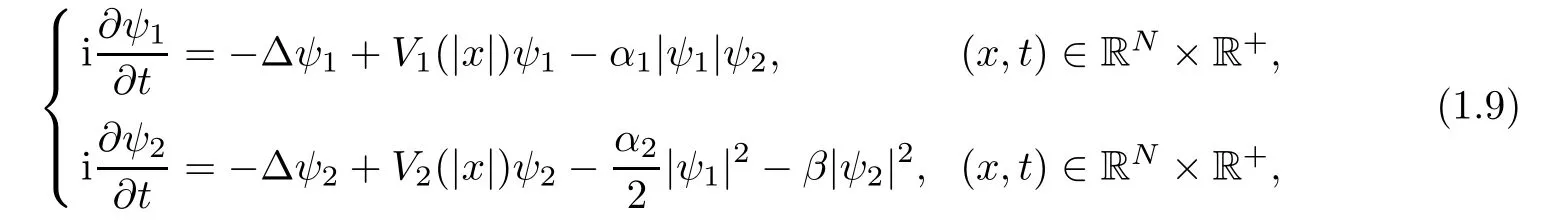
where ψjare the complex wave functions de fined in RNwhich for solitary waves,i.e.,localized solutions,must also decay at in fi nity.When α1=1,α2>0,β =0,(1.9)is just the case considered in[32]by Zhao,Zhao and Shi.They obtained the existence of ground state solutions for spatial dimension from two to fi ve and the continuous dependence on the parameter and asymptotic behavior of them.Also,applying a new technique of double saddle-node bifurcation they obtained multiple solutions with certain symmetry.
When N=1 and V1(|x|),V2(|x|)equal to constants in(1.1),(1.1)is very close to a coupled Schrödinger-KdV system.One can refer to[10,11,13,14]for details.
Therefore,we consider the case that when α1= α2= α >0 and β is arbitrary,i.e.,(1.1).Since β is arbitrary,our result can be easily extended to cover the case that β =0,which is just the coupled Schrödinger system(1.6)with χ(2)nonlinearities.Moreover,the motivation for which we consider(1.1)is that we will obtain a non-degeneracy result(see Proposition 2.2 later)which is of vital importance in this paper.
Furthermore,for the attractive case(that is,α>0)when V1(|x|)=V2(|x|)≡1,it is known that there are special positive solutions with two components being positive constant multipliying of the unique positive solution of the scalar square Schrödinger equation −∆u+u=u2,x∈RN.Thus,two components are in synchronization.This observation prompts the question of whether there are non radial synchronized vector solutions.Under some assumptions for V1(|x|)and V2(|x|)near in fi nity we construct in finitely many non-radial positive solutions for(1.1).
We suppose that V1(|x|)and V2(|x|)satisfy the following conditions.
(V1)There exist constants a∈R,s>1,and δ>0,such that as r→ ∞
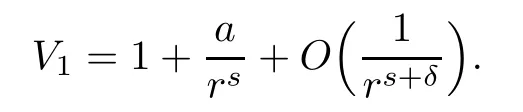
(V2)There exist constants b∈ R,t>1,and ǫ>0,such that as r→ ∞
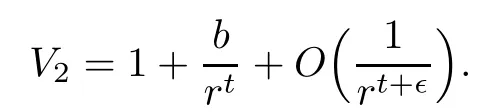
Our main result in this paper is as follows.
Theorem 1.1Let 2 ≤ N<6,α >0 and α > β.Assume that(V1)and(V2)are satis fied.Then system(1.1)has in finitely many non-radial positive solutions.
Next,we outline the main idea to prove our result.Denote the unique ground state U of
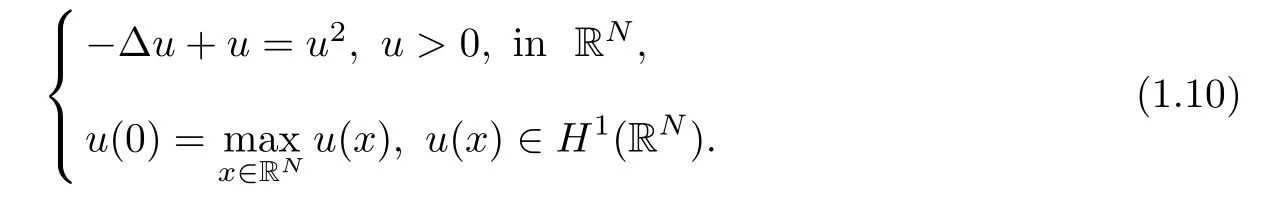
We will use the unique solution U(x)to construct the solutions for(1.1).Hereafter,for any function V(x)>0,the Sobolev space(RN)is endowed with the standard form
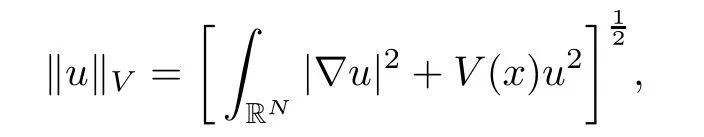
which is induced by the inner product
De fine H to be the product spacewith the norm
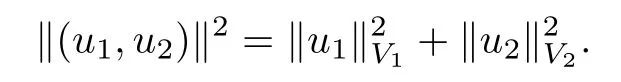
Note that the limit system for(1.1)is
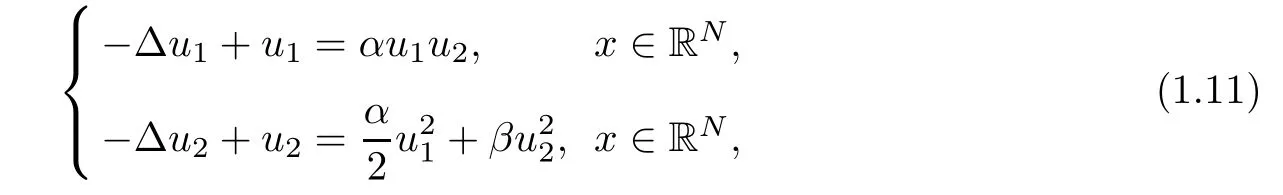
and that
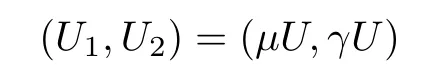
solves(1.11),provided that α > β,where
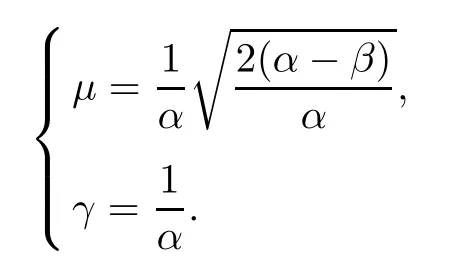
We will use(U1,U2)to construct the solutions for(1.1).Denote
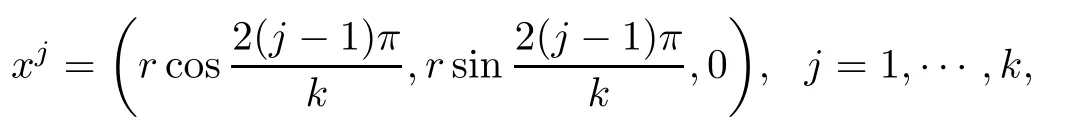
where 0 is the zero vector in RN−2,r∈[r0k lnk,r1k lnk]for some r1>r0>0.
Remark 1.2System(1.11)possesses a symmetry that if(U1,U2)is a solution of(1.11),so is(−U1,U2).
Denote
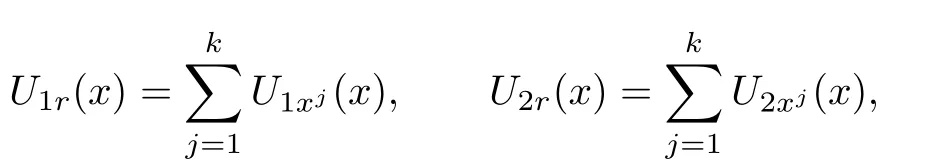
where U1xj(x)=U1(x−xj),U2xj(x)=U2(x−xj).
Set x=(x′,x′′)∈ R2× RN−2.De fine
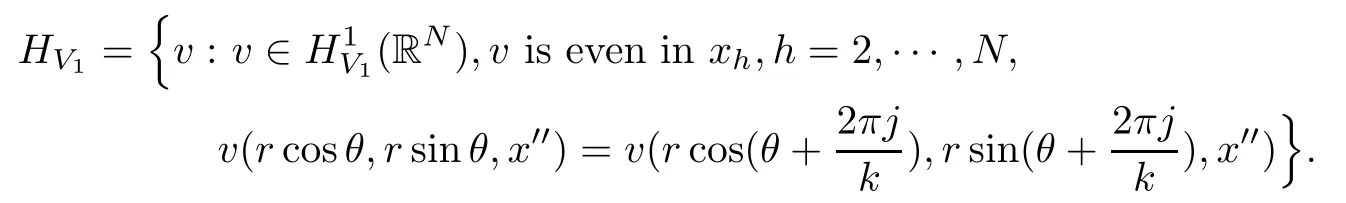
Similarly,we de fine HV2.
It is not difficult to check that(U1r,U2r)is in HV1×HV2.
In order to prove Theorem 1.1,we only need to check the following result.
Theorem 1.3Assume that the same conditions as those in Theorem 1.1 hold.Then there exists an integer k0>0,such that for any integer k≥k0,(1.1)has a solution(u1k,u2k)of the form
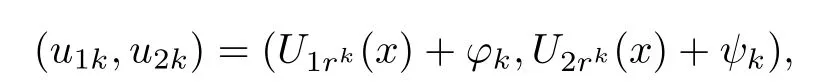
where(ϕk,ψk)∈(RN)×(RN),rk∈ [r0klnk,r1k lnk]for some constants r1>r0>0 and as k→+∞,
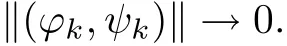
In Theorem 1.3,we construct in finitely many non-radial positive solutions(u1k,u2k)for system(1.1).The existence of synchronized solutions of(1.1)are guaranteed by the constructions,since the essential supports of the two components u1kand u2kare both placed in the same locations.It is easy for us to see that the larger the k is,the more synchronized these components are.
Set Uκbe the unique solution of the following problem

It is well-known that Uκis non-degenerate and Uκ=U(|x|),<0.
Remark 1.4It follows from Theorem 1.3 that system(1.1)has solutions with a large number of bumps near in fi nity.Thus,the energy of these solutions can be very large.
In the sequel,we will apply the finite dimensional reduction method to prove our main result.Since there is no small parameter in system(1.1),here we adopt the main idea introduced by[29],by using k,the number of the bumps of the solutions,as a parameter in the construction of spike solutions for(1.1).To our best knowledge,it is the first time to apply the finite dimensional reduction method to study(1.1).Our result exhibits a new phenomenon for the coupled Schrödinger system with χ(2)nonlinearities.
The structure of this paper is as follows.In Section 2,we do some preliminaries,speci fi cally we do the finite dimensional reduction.We will prove our main result in Section 3.In the sequel,for simplicity of notations we writeRf to mean the Lebesgue integral of f(x)in RN.
2 Some Preliminaries
In this section,we mainly do some preliminaries for section 3 to prove the main result.In fact,we mainly carry out the finite dimensional reduction.Let
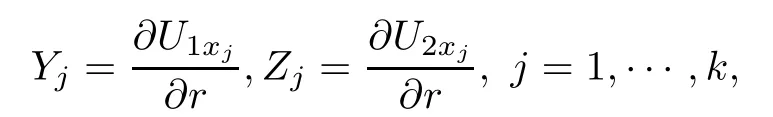
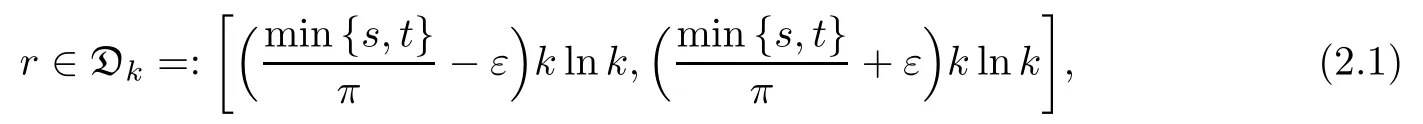
where ε>0 is a small constant.
Note that the energy functional corresponding to(1.1)is

Then I∈C2(H,R)and its critical points are solutions of(1.1).
De fine
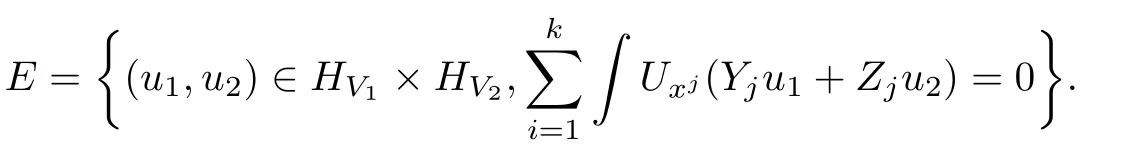
Set
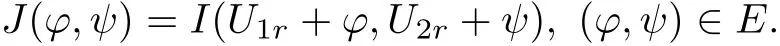
We can expand J(ϕ,ψ)as follows:
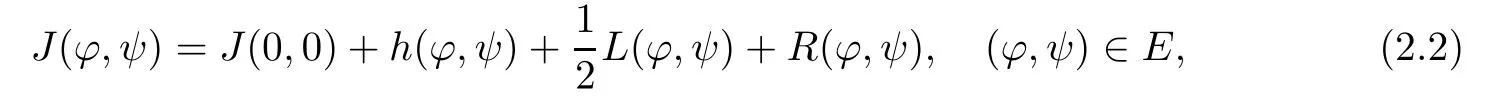
where

and

In order to get a critical point(ϕ,ψ) ∈ E of J(ϕ,ψ),we need to examine each term in the expansion(2.2).
It is easy to con fi rm that
is a bounded bi-linear functional in E.Hence,there exists a bounded linear operator L from E to E,such that
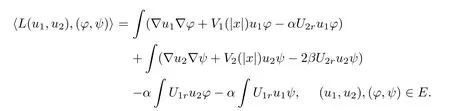
By the analysis above,we can obtain the following result.
Lemma 2.1There exists a constant C>0,independent of k,such that for any r∈Dk,

In order to show the invertibility of L in E, first we need the following non-degenerate result which is of great interest independently.
Proposition 2.2For any α >0 and α > β,(U1,U2)is non-degenerate for system(1.11)in H1(RN)× H1(RN)in the sense that the kernel is given by span{(η(α,β))|i=2,···,N+1},where η(α,β)6=0.
ProofBy using the same arguments in[3],we consider the weighted eigenvalue problem in λ:−∆φ+φ = λUφ.There is a sequence of eigenvalues 1= λ1< λ2= λ3= ···= λN+1=2< λN+2≤ ···with associated eigenfunctions φksatisfyingRRNUφiφjdx=0 for i 6=j.Denote φi=for i=2,3,···,N+1,then,for α > β,the linearization of equation(1.11)at(U1,U2)may write as follows
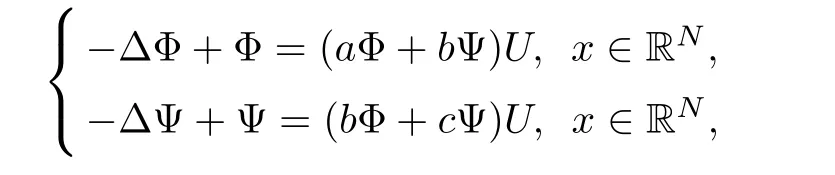
where

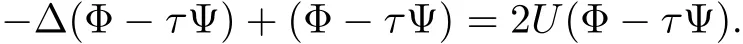
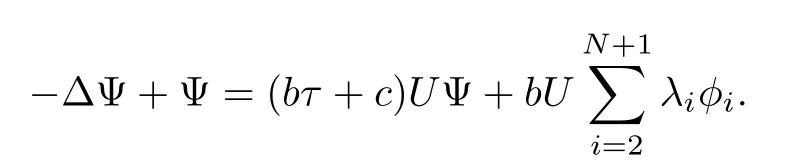
First we need to get the following estimates which will be used later.
Lemma 2.3For any p ≥ 1,there is a θ>0,such that

ProofSince the proof of this lemma is similar to Lemma A.1 in[21],here we omit it.
Now,we prove the operator L is invertible in E.
Lemma 2.4There exists a constant ρ>0,independent of k,satisfying that for any r∈Dk,
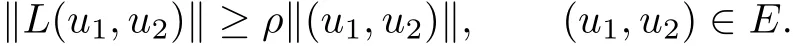
ProofWe argue it by contradiction.Suppose that there are k→∞,rk∈Dk,and(u1k,u2k)∈E with
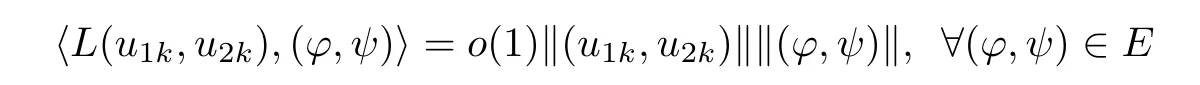
and k(u1k,u2k)k2=k.
Recall that
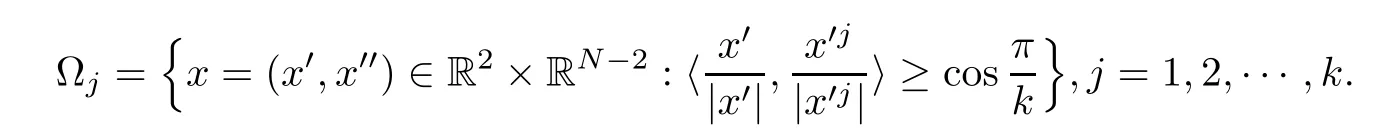
By symmetry,we have
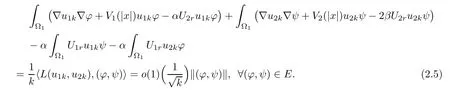
Especially,
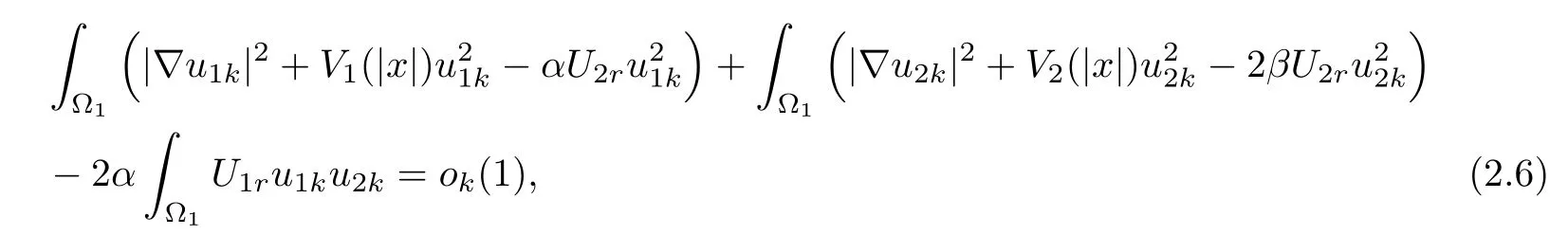
and
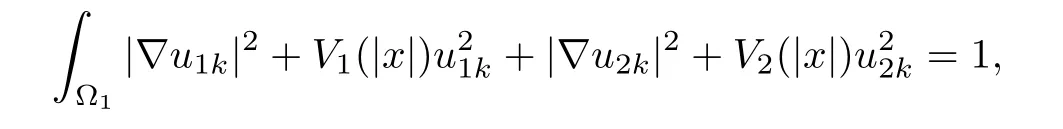
where ok(1)→0 as k→∞.Set(x)=u1k(x−x1),(x)=u2k(x−x1),then for any R>0,since dist(x1,∂Ω1)=rsin≥ C lnk→ +∞,BR(x1)⊂ Ω1,i.e.,
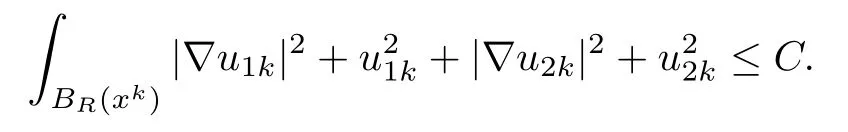
One can get
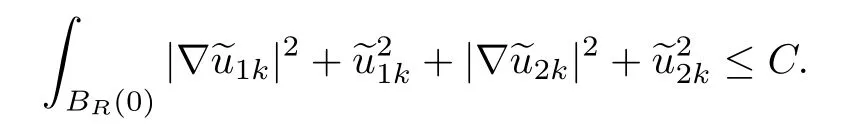
So we suppose that there exist u1,u2∈H1(RN),such that as k→+∞,
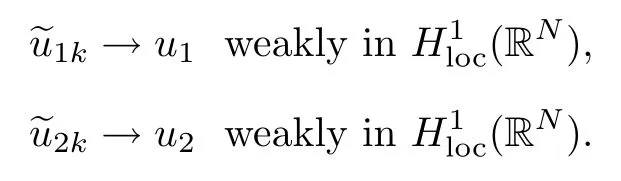
Hence,we have

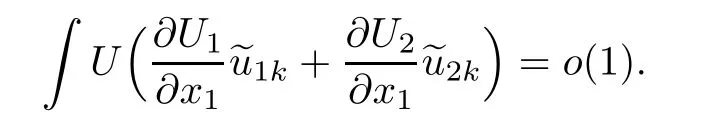
So,u1and u2satisfy
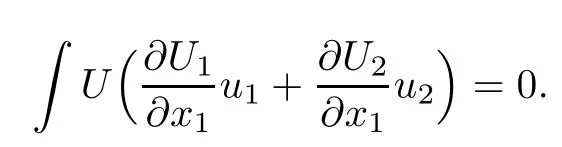
Now,we claim that(u1,u2)satis fies
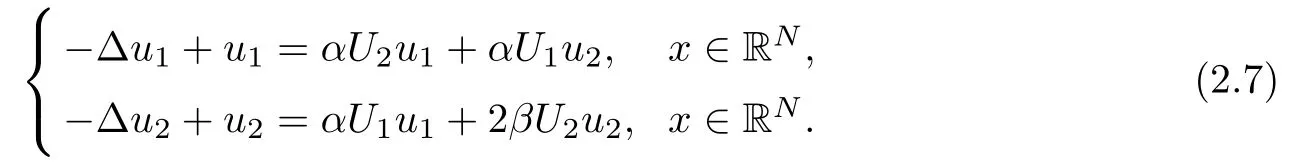
Indeed,we set
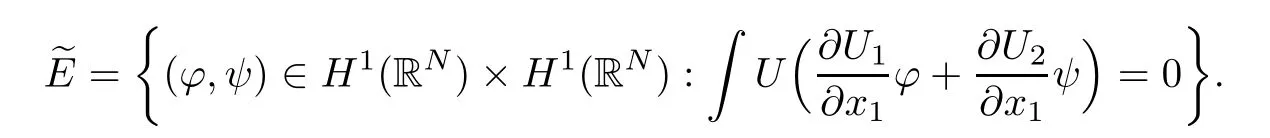

and
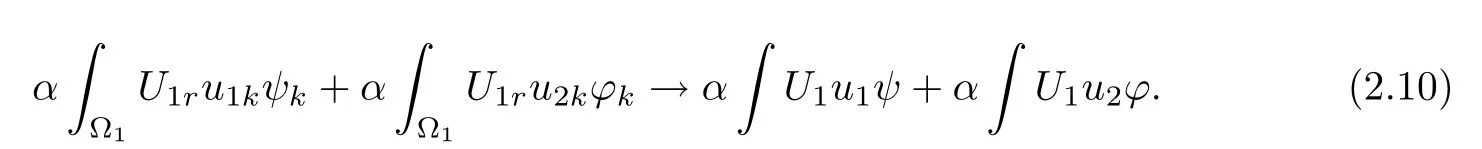
Inserting(2.8),(2.9),(2.10)into(2.5),we have
However,since u1and u2are even in xi,i=2,···,N,(2.11)holds for any function(ϕ,ψ)∈(BR(0))×(BR(0)),which is odd in xi,i=2,···,N.Hence,(2.11)holds for any(ϕ,ψ) ∈(BR(0))×(BR(0))∩.Using the density of(BR(0))×(BR(0))in H1(RN)×H1(RN),we see
We see that(U1,U2)=(µU,γU)and U solves(1.10).It is easy to check that(2.12)holds forTherefore,(2.12)is true for(ϕ,ψ)∈ H1(RN)×H1(RN).
So,we have proved that(u1,u2)satis fies(2.7).
From Proposition 2.2,(U1,U2)is non-degenerate.Since the space of functions we considered is even in xi(i=2,···,N),the kernel of(U1,U2)is given by the one dimensionalThus we see thatfor some C,which implies that(u1,u2)=(0,0),since(u1,u2)satis fies(2.7).
Consequently,
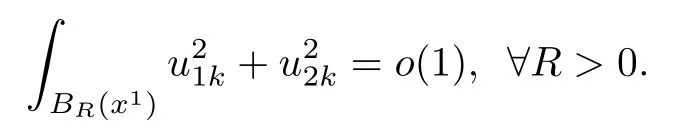
Now using Lemma 2.3,we obtain

Thus,
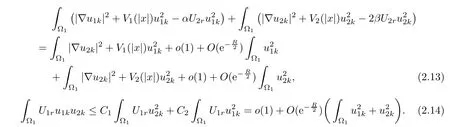
Inserting(2.13),(2.14)into(2.6),we have
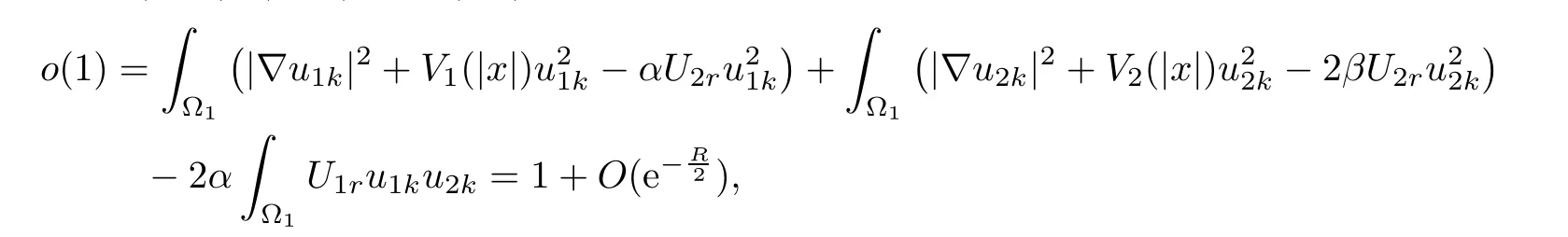
which is impossible for large R.
As a result,we get a contradiction.
Now we come to the main result of this section.
Proposition 2.5There exists an integer k0>0,such that for each k≥k0,there is a C1map from Dkto HV1×HV2:(ϕ,ψ)=(ϕ(r),ψ(r)),r=|x1|satisfying(ϕ,ψ)∈ E,and
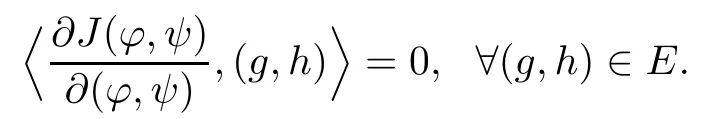
Furthermore,there exists a positive constant C,such that
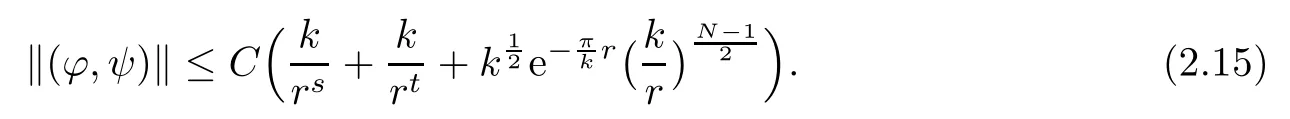
In order to apply the contraction mapping theorem to prove Proposition 2.5, first we have to obtain the following three lemmas.
Lemma 2.6There is a constant C>0 independent of k such that

ProofBy direct calculation,we find that for any(ϕ,ψ)∈ E,

and similarly,
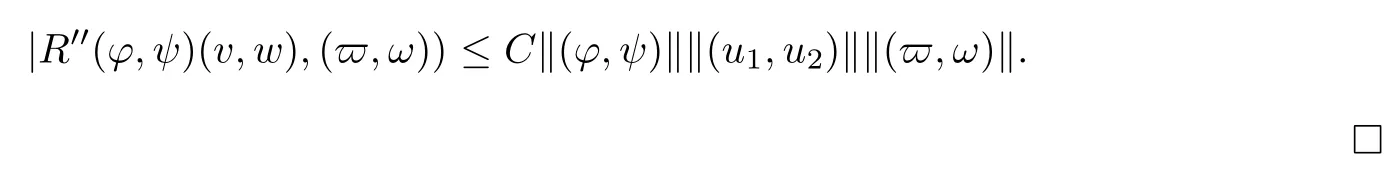
Lemma 2.7There exists a constant C>0 independent of k,such that
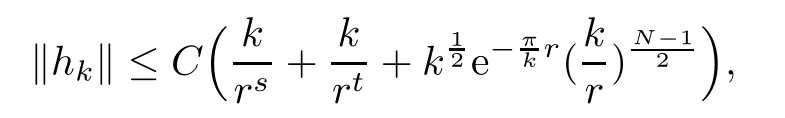
provided k≥k0for some integer k0>0.
ProofNotice that
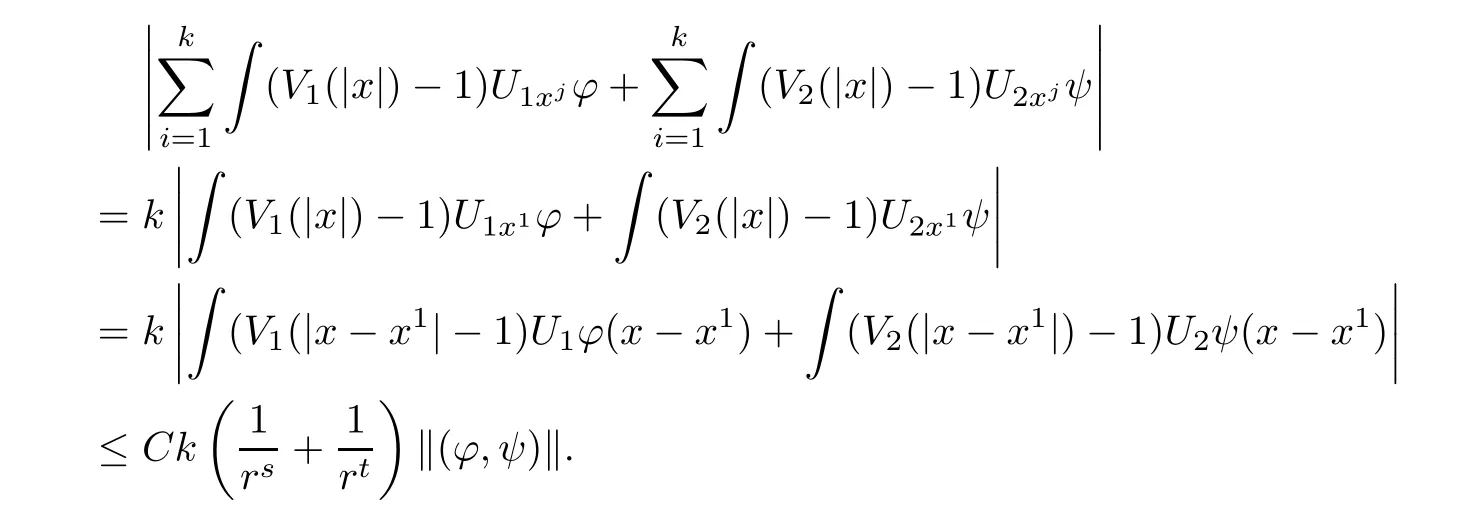
Now,we estimate
By symmetry and using the fact U1xi≤U1x1,U2xi≤U2x1,x∈Ω1and Lemma 2.3,we have
where we have used the fact that
Similarly,we can get

Finally,since U1=,we obtain
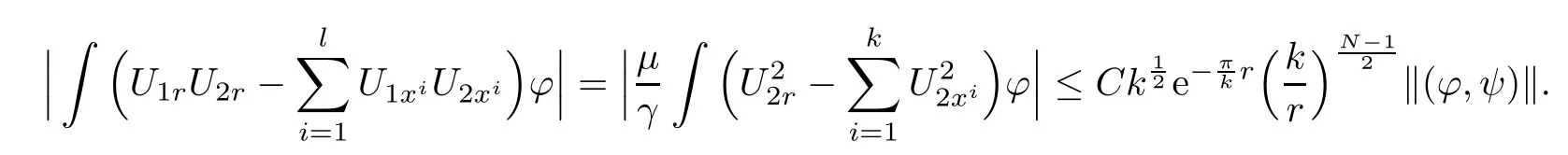
Hence,
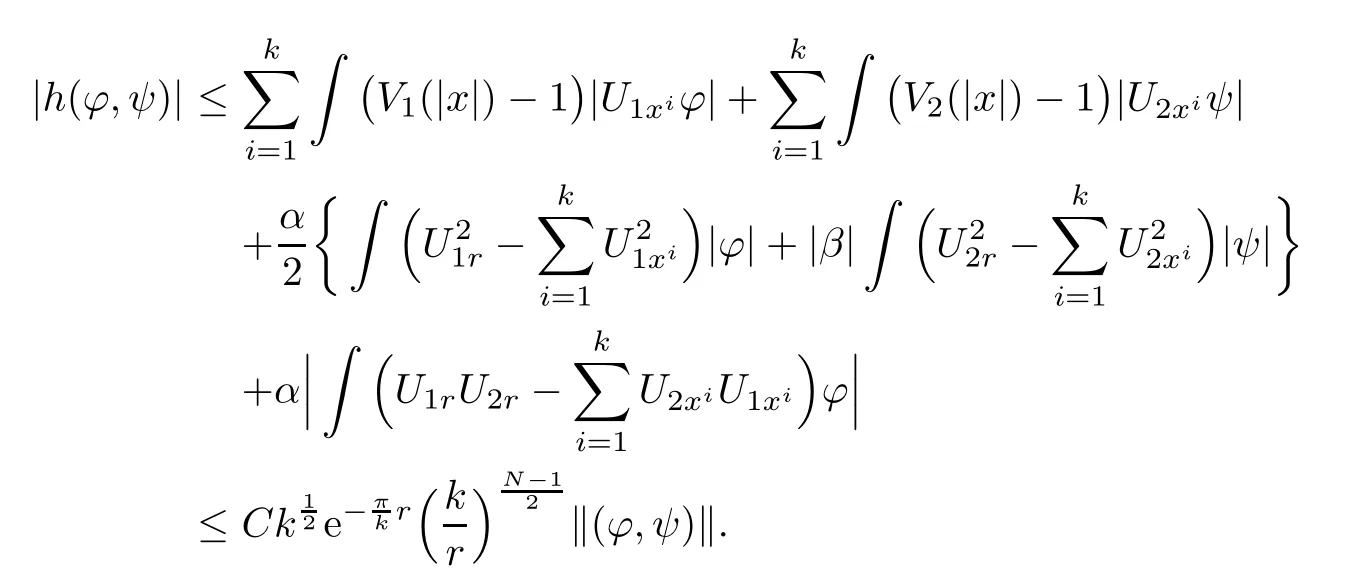
Now we are in position to prove Proposition 2.5.
Proof of Proposition 2.5We will use the contraction theorem to prove it.By Lemma 2.7,h(ϕ,ψ)is a bounded bi-linear functional in E.We may get by Reisz theorem that there is an hk∈E,such that
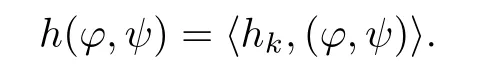
So, finding a critical point for J(ϕ,ψ)is equivalent to solving

By Lemma 2.4,L is invertible.Hence,(2.17)can be revised as
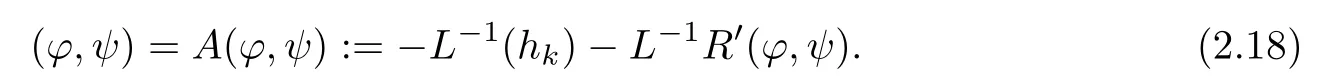
Let
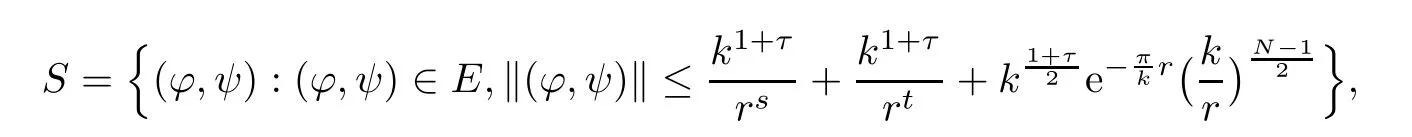
where τ>0 is small.Next,we verify that A is a contraction map from S to itself.In fact,for any(ϕ,ψ)∈ S,by Lemmas 2.6 and 2.7,for k large,we have
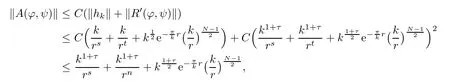
and for any(ϕ1,ψ1),(ϕ2,ψ2)∈ S,
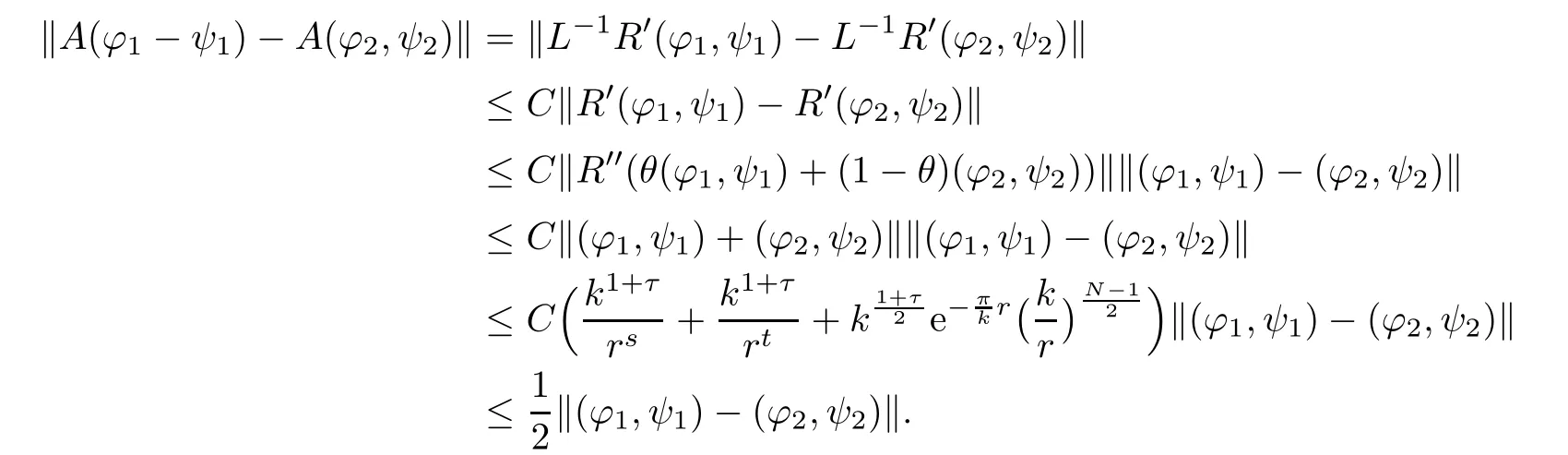
Then,we obtain the result from the contracting mapping theorem.Finally,by(2.18),we have
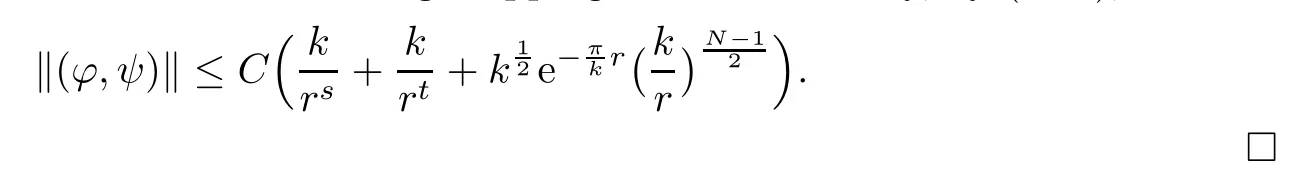
3 Proof of Our Main Result
In this section,we mainly prove our result.
First we expand the energy I(U1r,U2r),where

Lemma 3.1There exists a small constant τ>0 satisfying
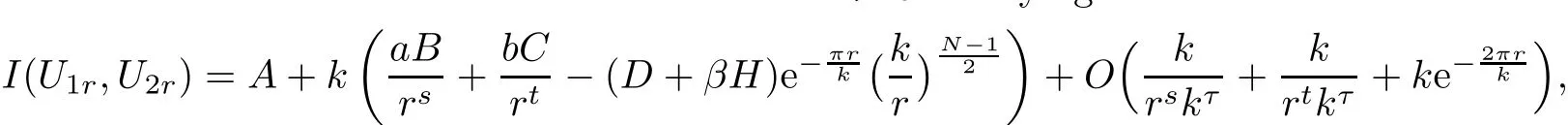
ProofIt is not difficult to get
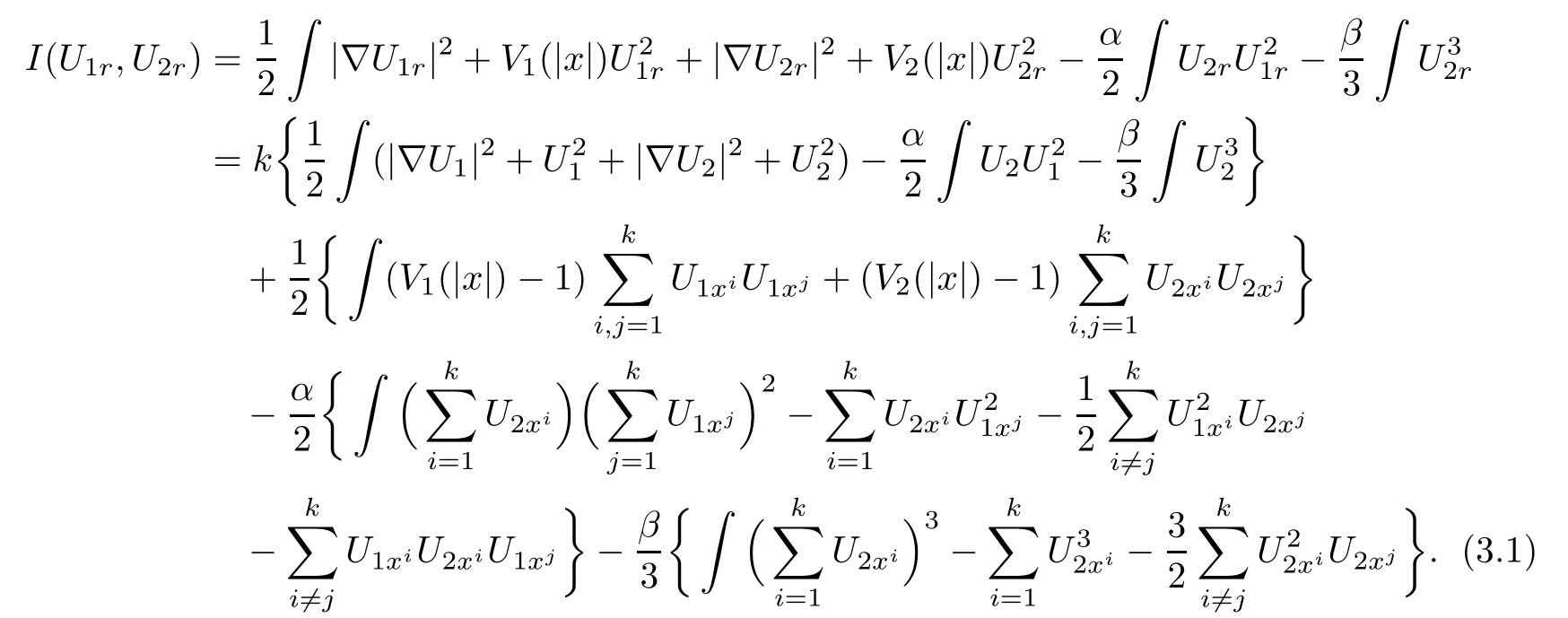
Then,we discuss each term in(3.1).By Lemma 2.3 and the knowledge of symmetry,we have
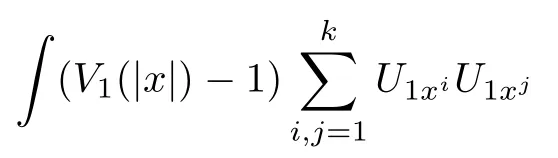
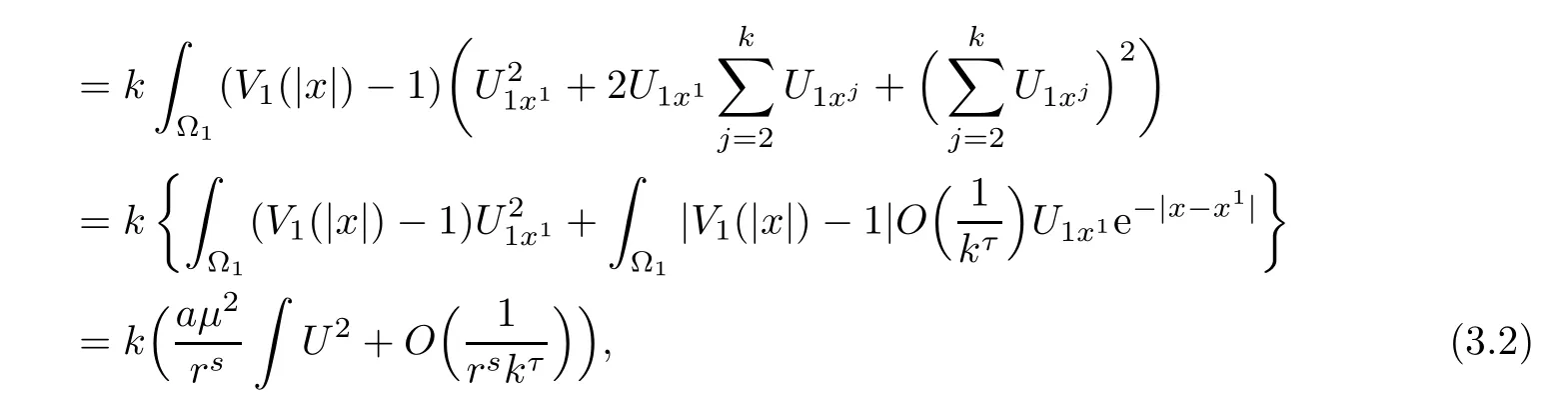
where τ>0 is a small constant.Similarly,we can estimate
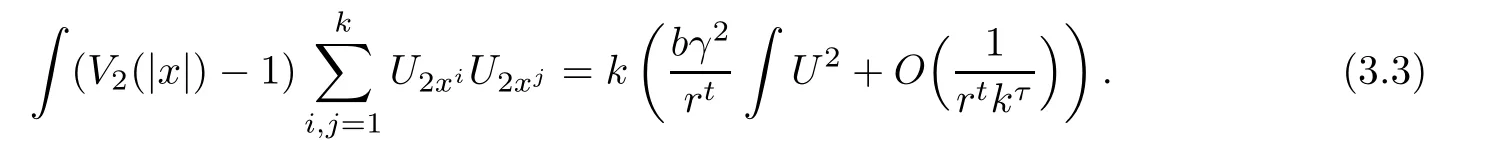
From Lemma 2.3,we have
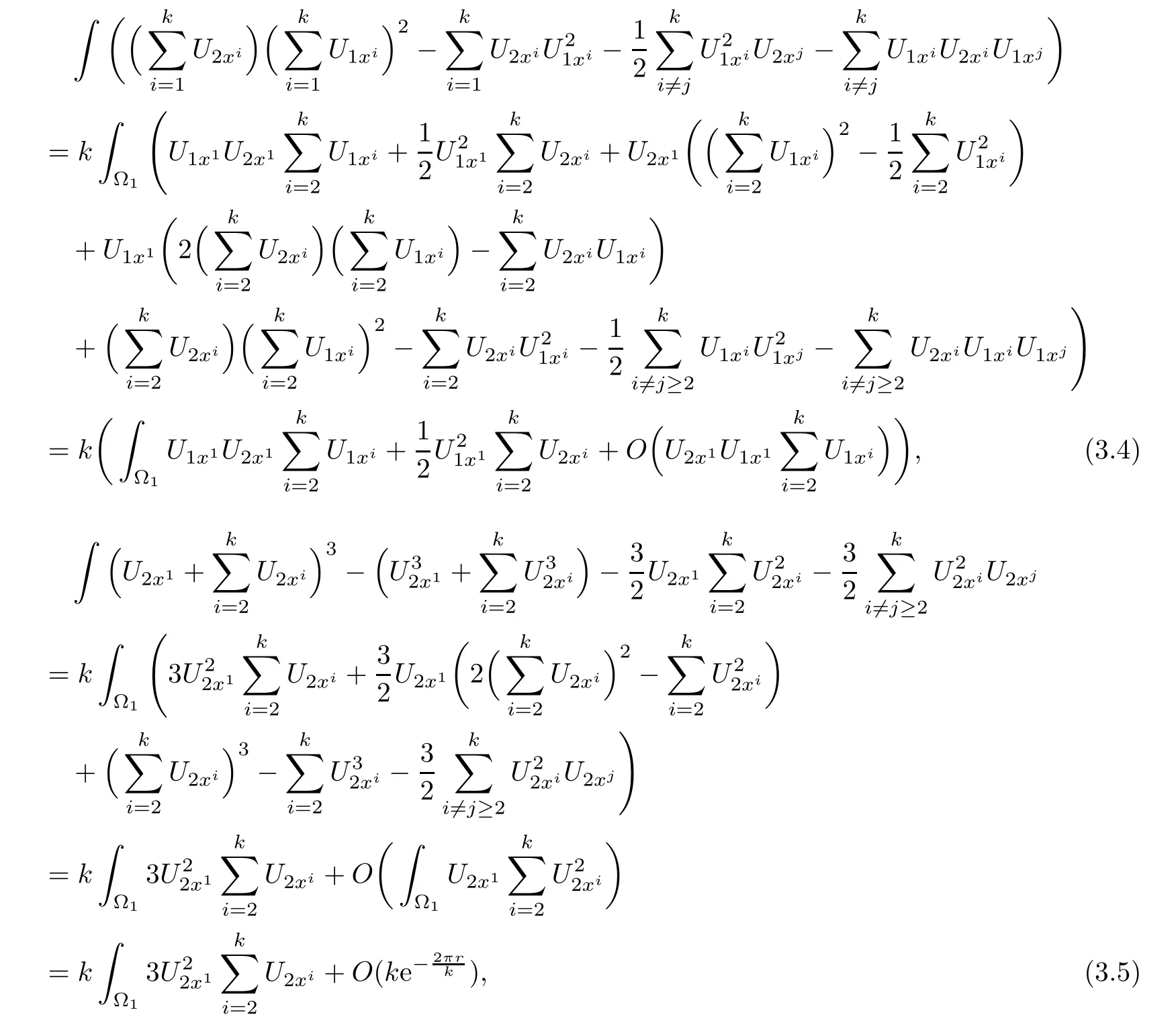
and
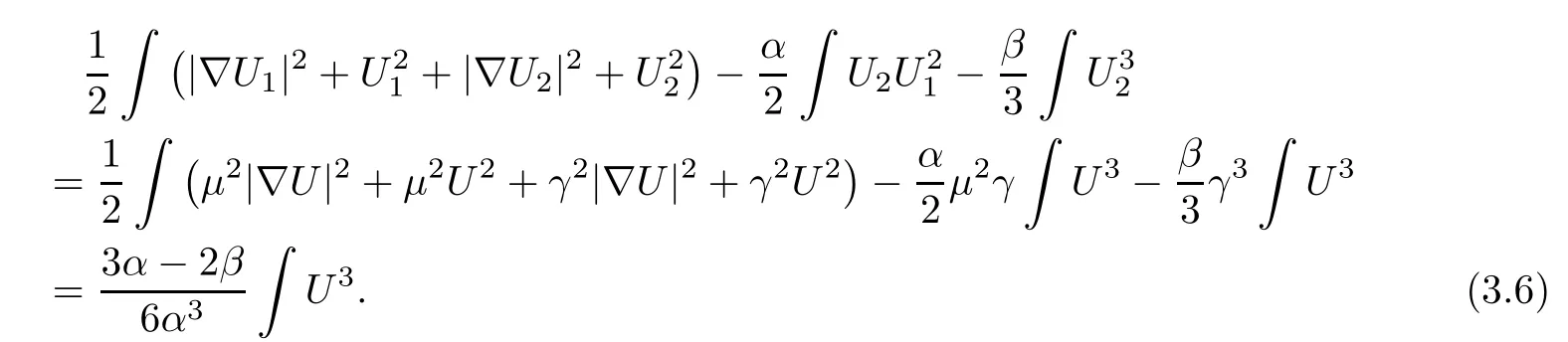
Hence,we have
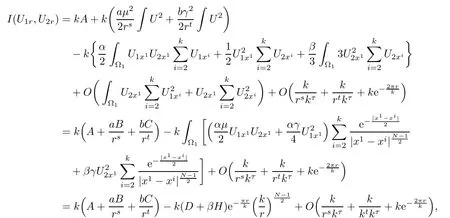
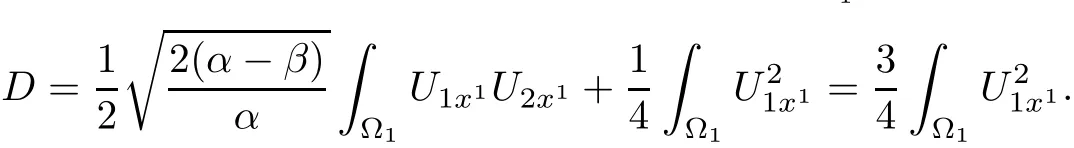
For α > β,using the expression of U1x1and U2x1,it is easy to see that D+ βH>0.
Hence,we complete the proof.
Now,we will apply the results obtained in Section 2 and Lemma 3.1 to prove our main result.
Proof of Theorem 1.3Let(ϕr,ψr)=(ϕ(r),ψ(r))be the map obtained in Proposition 2.5.De fine F(r)=I(Vr+ϕr,Wr+ψr), ∀r∈ Dk.Using the same arguments used in Proposition 2 in[8]or Proposition 3 in[20],we can easily check that for k sufficiently large,if r is a critical point of F(r),then(U1r+ϕr,U2r+ψr)is a critical point of I.
It follows from Lemma 2.1 and Lemma 2.6 that
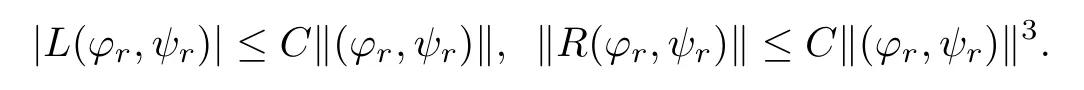
So by Lemma 3.1 we have

We prove the theorem only for the case s=t,since the other case is similar.Suppose s=t,then
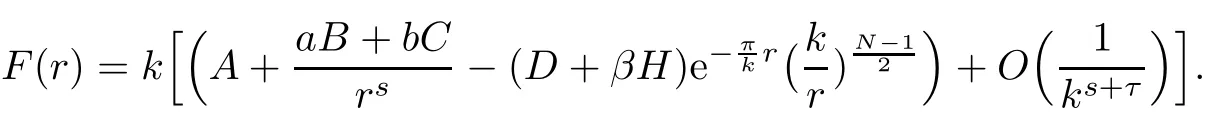
Note that α > β and(D+ βH)>0.Let Dkbe de fined in(2.1).De fine
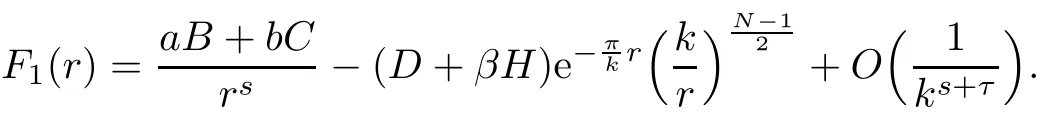
Next we discuss the following maximization problem

Suppose that(3.7)has a maximizerin Dk,we will verifyis an interior point of Dk.
We check that the function

By direct computation,we have
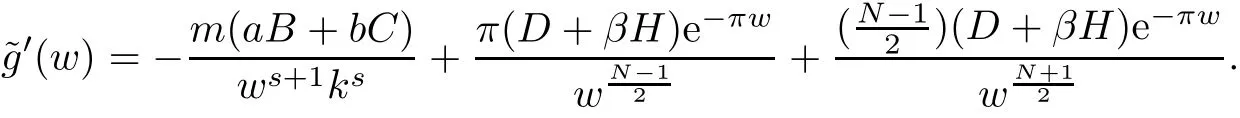
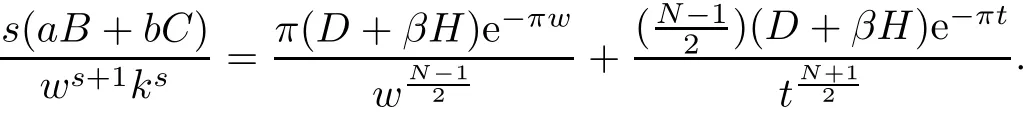
Hence,the function
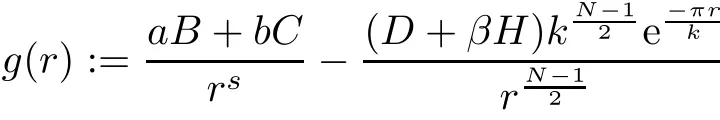
has a maximum point
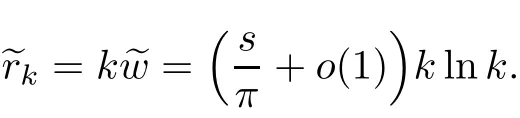
Therefore,it deduces from the expression of F1(r)that the maximizeris an interior point of Dk,if we choose ε>0 small in(2.1).
At last,we claim that u1rk=U1rk+ϕrkand u2rk=U2rk+ψrkare positive.
In fact,by regularity theory,We may obtain that(ϕrk,ψrk)tends to zero in L∞-norm as k → ∞.Assume that(u1rk)−=max{−u2rk,0},(u1rk)−=max{−u2rk,0},then we get that(u1rk)−and(u2rk)−tend to zero as k → ∞.If u1rk<0,then U1rk(x)≤ −ϕrk(x)=o(1)as k → ∞.Then,U2rk=µγU1rk→ o(1),as k → ∞.From hI′(u1rk,u2rk),((u1rk)−,0)i=0,we have that
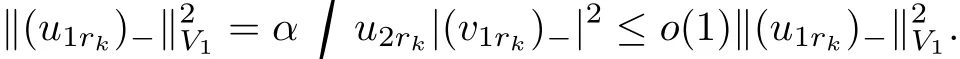
Hence,(u1rk)−=0.We have u1rk=(u1rk)+≥ 0.Then,by the strong maximum principle,u1rk>0.
Next,we prove that u2rk>0.
If α > β >0,we prove it by contradiction argument.Assume that there exists x0such thatThen ∆u2rk(x)|x=x0≤0.It follows that
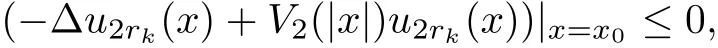
If α >0 and β ≤ 0,we also prove it by contradiction argument.Assume that there exists x0such thatObserving that u2rk(x0)=o(1),as k→ ∞,then∆u2rk(x)|x=x0≥0.So we have
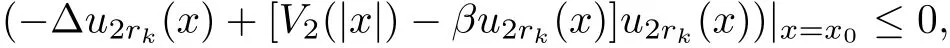
as k→∞,which also contradicts to

AcknowledgementsThe authors sincerely thank Prof.S.Peng for his helpful discussions and suggestions.
 Acta Mathematica Scientia(English Series)2020年1期
Acta Mathematica Scientia(English Series)2020年1期
- Acta Mathematica Scientia(English Series)的其它文章
- HILBERT PROBLEM 15 AND NONSTANDARD ANALYSIS(I)∗
- COMPLEX SYMMETRIC TOEPLITZ OPERATORS ON THE UNIT POLYDISK AND THE UNIT BALL∗
- THE BOUNDEDNESS FOR COMMUTATORS OF ANISOTROPIC CALDER´ON-ZYGMUND OPERATORS∗
- GROUND STATES FOR FRACTIONAL SCHR¨ODINGER EQUATIONS WITH ELECTROMAGNETIC FIELDS AND CRITICAL GROWTH∗
- MULTIPLE JEEPS PROBLEM WITH CONTAINER RESTRICTION∗
- THE EXISTENCE AND LOCAL UNIQUENESS OF MULTI-PEAK POSITIVE SOLUTIONS TO A CLASS OF KIRCHHOFF EQUATION∗
