平面向量常见典型考题赏析

■张文伟

题型1：平面向量的基本概念

与平面向量的概念有关命题真假的判定问题，其关键在于理解平面向量的概念，还应注意零向量的特殊性以及两个向量相等必须满足：①模相等，②方向相同。平面向量有关概念的核心：①向量定义的核心是方向和长度，②非零共线向量的核心是方向相同或相反，长度没有限制，③相等向量的核心是方向相同且长度相等，④单位向量的核心是方向没有限制，但长度都是一个单位长度，⑤零向量的核心是方向没有限制，长度是0，规定零向量与任何向量共线，⑥向量与数量不同，数量可以比较大小，向量不能比较大小，但向量的模是非负实数，可以比较大小。

例1 下列说法正确的是( )。

A.方向相同的向量叫作相等向量

B.共线向量是在同一条直线上的向量

C.零向量的长度等于0

解：长度相等且方向相同的向量叫作相等向量，A不正确。方向相同或相反的非零向量叫作共线向量，但共线向量不一定在同一条直线上，B不正确。显然，C正确。当时，所在的直线与所在的直线可能重合，D不正确。应选C。

跟踪训练1：有下列命题：①若|a|=|b|，则a=b；②若，则四边形A B C D是平行四边形；③若m=n，n=k，则m=k；④若a∥b，b∥c，则a∥c。

其中假命题的个数是( )。

A.1 B.2

C.3 D.4

提示：对于①，|a|=|b|，a，b的方向不确定，则a，b不一定相等，①错误。对于②，若模相等，即则向量的方向不一定相同，所以四边形A B C D不一定是平行四边形，②错误。对于③，若m=n，n=k，则m=k，③正确。对于④，若a∥b，b∥c，则当b=0时，a∥c不一定成立，④错误。假命题是①②④。应选C。

题型2：平面向量的线性运算

用已知向量表示另外一些向量，要利用向量的加法、减法、数乘运算，还要利用平面几何的一些定理。在求向量时，要尽可能转化到平行四边形或三角形中，利用平行四边形法则、三角形法则，利用三角形中位线、相似三角形对应边成比例等平面几何性质，把未知向量转化为与已知向量有直接关系的向量来求解。

例2 如图1，在△A B C中，点M为A C的中点，点N在A B上，点P在线段

图1

解：由向量运算法则，可得应选D。

跟踪训练2：如图2，在△A B C中，点D在B C边上且C D=2D B，点E在A D上且A D=3A E，试用表示

图2

提示：由平面向量的三角形法则及向量共线的性质，可得

题型3：共线向量定理及其应用

利用共线向量定理可以证明向量共线，也可以由向量共线求参数的值。若a，b不共线，则λ a+μb=0的充要条件是λ=μ=0，这一结论结合待定系数法应用非常广泛。证明三点共线：若，则A，B，C三点共线。

例3 已知a，b是不共线向量，，若A，B，C三点共线，则λ，μ的关系一定成立的是( )。

A.λμ=1 B.λμ=-1

C.λ-μ=-1 D.λ+μ=2

解：若A，B，C_三点共线，则存在一个实数t，使得，即λ a+b=t a+μt b。因为a，b是不共线向量，所以消去参，数t可得λμ=1。应选A。

跟踪训练3：设e1与e2是两个不共线向量，向量3e1-2k e2，若A，B，D三点共线，则k的值为____。

提示：由题意可知A，B，D三点共线，故必存在一个实数λ，使得又(k e1+e2)=(3-k)e1-(2k+1)e2，所以3e1+2e2=λ(3-k)e1-λ(2k+1)e2。由e1与e2不共线，可得解得k=

题型4：平面向量基本定理的应用

应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算。用平面向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决问题。

例4 如图3，在直角梯形A B C D中，A B=2A D=2D C，E为B C边上一点为A E的中点，则

图3

解：取A B的中点为G，连接D G，C G。易知四边形D C B G为平行四边形，所以由此可得

跟踪训练4：如图4所示，在△A B C中，

点P是A B上一点，且点Q是B C的中点，A Q与C P的交点为M，又，则实数t的值为_______。

图4

提示：因 为所以，所 以 2可知P为线段A B的一个三等分点(靠近A点)。由A，M，Q三点共线，可设因为由此解得t故t的值是

题型5：平面向量的数量积问题

已知两个非零向量a和b，它们的夹角为θ，把数量叫作向量a和b的数量积(或内积)，记作a·b，即a·b=，规定a·0=0。

例5 如图5，在等腰直角△A B C中，∠A B C=90°，A B=B C=2，M，N(不与A，C重合)为A C边上的两个动点，且满足，则的取值范围为( )。0＜a＜1，N(a+1，1-a)，可得

图5

解：以B为坐标原点，B C所在直线为x轴，建立直角坐标系x B y，则B(0，0)，直线A C的方程为x+y=2。设M(a，2-a)，则，所以a(a+1)+(2-a)(1-a)=2a2-2a+2=。由0＜a＜1，可知当时取得最小值为即易得，故的取值范围为应选C。

跟踪训练5：在△A B C中，B C边上的中线A D的长为2，点P是△A B C_所在平面上的任一点，则的最小值为( )。

A.1 B.2

C.-2 D.-1

提示：建立如图6所示的平面直角坐标系x D y，使得点D在坐标原点处，点A在y轴上，则A(0，2)。

图6

设点P的坐标为(x，y)，则所以2≥-2，当且仅当x=0，y=1时等号成立。

故P的最小值为-2。应选C。

题型6：向量的投影问题

已知两个非零向量a与b，θ是a与b的夹角，|a|cosθ(或|b|cosθ)叫作向量a在b方向上(或b在a方向上)的投影。

例6 已 知 点A(-1，1)，B(1，2)，C(-2，-1)，D(3，4)，则向量在方向上的投影是____。

解：依题意可得，因此向量在方向上的投影是

跟踪训练6：已知两个单位向量a和b的夹角为60°，则向量a-b在向量a方向上的投影是____。

提示：由两个单位向量a和b的夹角为60°，可得，所以向量a-b在向量a方向上的投影为

题型7：与向量有关的面积问题

解答这类问题要注意平面几何知识的应用以及对数学式子的几何意义的挖掘。

例7 如图7所示，设O是△A B C内部一点，且，求△A B C与△A O C的面积之比。

图7

解：取A C的中点为D，连接_O D，则，由此可得，所以O是A C边上的中线B D的中点，可知S△A B C=2S△A O C，即△A B C与△A O C的面积之比为2∶1。

_跟踪训练7：已知O是△A B C内部一点，且∠B A C=60°，则△O B C的面积是____。

提示：由O，可得所以O为三角形的重心，所以△O B C的面积为△A B C面积的。由2。由∠B A C=60°，可得因为△A B C的面积为，所以△O B C的面积为

题型8：向量在解析几何中的应用

向量在解析几何问题中的出现，多用于“包装”，解决此类问题关键是利用向量的意义、运算，脱去“向量外衣”。利用向量a⊥b⇔a·b=0，向量a∥b⇔a=λ b(b≠0)，可解决垂直，平行问题。

例8 已知A B为圆C：(x-1)2+y2=1的直径，点P为直线x-y+1=0上任一点，则的最小值为( )。

解：由题意可设点A(1+cosθ，sinθ)，点P(x，x+1)，则点B(1-cosθ，-sinθ)，可得(1-cosθ-x，-sinθ-x-1)，所以(sinθ-x-1)(-sinθ-x-1)=(1-x)2-cos2θ+(-x-1)2-sin2θ=2x2+1≥1，当且仅当x=0时等号成立。应选A。

跟踪训练8：已知圆C：x2+y2-2x-，点A(0，m)(m＞0)，A，B两点关于x轴对称。若圆C上存在点M，使得，则当m取得最大值时，点M的坐标是( )。

提示：由题意可得圆的方程为(x-1)2+，点B(0，-m)。

设M(x，y)。由于，所以(x，y-m)·(x，y+m)=0，可得x2+y2-m2=0，即m2=x2+y2。因为x2+y2表示圆C上的点到原点距离的平方，所以连接O C，并延长和圆C相交，交点即为M(图略)，此时m2最大，m也最大。容易求得|OM|=3，∠MO x=60°，所以xM=3×。应选C。

题型9：向量在平面几何中的应用

利用平面向量解决平面几何问题，可建立平面直角坐标系，这样可以使向量的运算更简便一些。在解决这类问题时，共线向量定理和平面向量基本定理起主导作用。

例9 如图8，在四边形A B C D中，点E，F分别是边A D，B C的中点，设。若则( )。

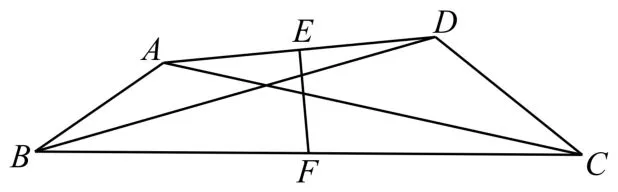
图8

A.2m-n=1 B.2m-2n=1

C.m-2n=1D.2n-2m=1

解：由 题 意 可 得因为点E，F分别是边A D，B C的中点，所以上述两式相加可得，两边平方可得所 以，即由此可得，所以，即2n-2m=1。应选D。

跟踪训练9：已知是非零向量，且满足，则△A B C的形状为( )。

A.等腰三角形B.直角三角形

C.等边三角形D.等腰直角三角形

提示：由，可得可得，可得A=60°。由上可知△A B C为等边三角形。应选C。

题型10：向量与三角函数的综合问题

这类问题可应用向量共线，垂直或等式成立，得到三角函数的关系式，再利用三角函数在定义域内的有界性求解。

例10 在△A B C中，设A，B，C的对边分别为a，b，c，向量m=(cosA，sinA)，n=，且|m+n|=2。

(1)求角A的大小。

解：(1)由可 得|m+n|=积。

由|m+n|=2，可得由0＜A＜π，可得所以A-，即

故S△A B C=16。

跟踪训练10：在平面直角坐标系x O y中，已知向量

(1)若m⊥n，求tanx的值。

(2)若m与n的夹角为，求x的值。

提示：(1)因为m⊥n，所以m·n=0，即

(2)因为|m|=|n|=1，所以m·n=，即，所以

题型11：向量与三角形的“四心”问题

例11 在 △A B C中，点G是△A B C的重心，则的最小值是( )。

解：设B C的中点为D。因为点G是△A B C的重心，所以

跟踪训练11：如图9，已知△A B C外接圆的圆心为O，A为钝角，M是B C边的中点，则等于( )。

图9

A.3 B.4

C.5 D.6

提示：由M是B C边的中点，可得由O是△A B C外接圆的圆心，可得同理可得，。故。应选C。

题型12：与向量有关的轨迹问题

与向量有关的轨迹问题主要涉及三角形的“四心”问题、直线与圆问题等。

例12 已知O是平面上的一定点，A，B，C是平面上不共线的三个定点，若动点P满足则点P的轨迹一定通过△A B C的( )。

A.内心 B.外心

C.重心 D.垂心

解：由题意可得即根据平行四边形法则，可知(D为B C的中点)，所以点P的轨迹必过△A B C的重心。应选C。

跟踪训练12：已知过点(0，1)的直线与圆x2+y2=4相交于A，B两点，若，则点P的轨迹方程为( )。

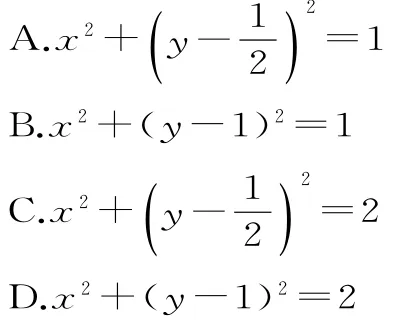
提示：设P(x，y)，A(x1，y1)，B(x2，y2)，过点(0，1)的直线方程为y=k x+1。由，可得(x，y)=(x1+x2，y1+y2)。把y=k x+1代入x2+y2=4，可得(1+k2)x2+2k x-3=0，则x1+x2=。同理可得。故x=所以x2+(y-1)2=1。应选B。