例谈伸缩变换在解高考题中的应用

广东省佛山市高明区教师发展中心(528500) 张文玲

一、定义引出

在高中数学选修4-4 第一讲中,有如下定义:设点P(x,y)是平面直角坐标系中的任意一点,在变换的作用下,点P(x,y)对应到点P′(x′,y′),称φ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.在它的作用下,可以实现平面图形的伸缩.

在此变换下,原来直角坐标系xOy中的点A(x1,y1),B(x2,y2),C(x3,y3)对应变为直角坐标系x′O′y′中的点A′(x1′,y1′),B′(x2′,y2′),C′(x3′,y3′),且有如下结论:

①若点A,B,C三点共线,则点A′,B′,C′三点也共线[1].

②若A,B,C三点共线且|AB|=λ|BC|(λ>0),则变换之后|A′B′|=λ|B′C′|(λ>0).故若点B为线段AC的中点,则点B′为线段A′C′的中点[1].

③若直线AB的斜率为k,则直线A′B′的斜率为mk[1].故两条平行直线经变换后仍然平行.

④两封闭图形的面积之比在变换前后不变.

在圆中有很多优美的性质,将椭圆伸缩变换为圆之后,就可以利用圆的性质来解决一些问题,简化了计算,使学生不再“望椭圆而生畏”.下面从圆的四个常见性质出发来解决一些涉及到椭圆的高考题目.

二、应用举例

(一)直径所对的圆周角是直角

例1(2019年高考全国Ⅱ卷理科第21 题)已知点A(−2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率之积为记M的轨迹为曲线C.

(1)求C的方程,并说明C是什么曲线;

(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.

(ⅰ)证明:∆PQG是直角三角形;

(ⅱ)求∆PQG面积的最大值.

解析第(1)问和第(2)问的第(ⅱ)小题略,下面考虑第(2)问的第(ⅰ)小题.

设点P(x0,y0),G(xG,yG),则Q(−x0,−y0),E(x0,0).设直线PQ的斜率为k(k >0),则直线QE的斜率为P,G,Q,E分别对应变为P′,G′,Q′,E′.所以变换后直线P′Q′的斜率为直线Q′E′的斜率为

因为P′Q′为直径,所以P′G′⊥Q′G′,所以直线P′G′的斜率为,所以

图1

因为直线PG的斜率为所以PQ⊥PG,∆PQG是直角三角形.

例2(2019年高考天津卷理科第18 题)设椭圆的左焦点为F,上顶点为B.已知椭圆的短轴长为4,离心率为

(1)求椭圆的方程;

(2)设点P在椭圆上,且异于椭圆的上、下顶点,点M为直线PB与x轴的交点,点N在y轴的负半轴上.若|ON|=|OF|(O为原点),且OP⊥MN,求直线PB的斜率.

解析第(1)问略,下面考虑第(2)问.

图2

设直线PB的方程为y=kx+2(k0),则可求得实施变换后变为所以直线P′B′的方程为

因为P′B′⊥P′D′,所以直线P′D′的方程为联立可得所以kO′P′=

因为M所以由题意得OP⊥MN,所以所以,所以,所以,即直线PB的斜率为

(二)的圆周角所对的弦为直径

例3(2019年高考北京卷文科第19 题)已知椭圆的右焦点为(1,0),且经过点A(0,1).

(1)求椭圆C的方程;

(2)设O为原点,直线l:y=kx+t(t≠±1)与椭圆C交于两个不同点P,Q,直线AP与x轴交于点M,直线AQ与x轴交于点N.若|OM|·|ON|= 2,求证:直线l经过定点.

解析第(1)问略,下面考虑第(2)问.

因为M,N两点均在x轴上,所以实施变换后两点的坐标均保持不变.所以|O′M′|·|O′N′|=|OM| · |ON|=2 =|O′A′|2且O′A′⊥M′N′,所以∠M′A′N′= 90°即∠Q′A′P′= 90°,所以P′Q′为圆x′2+y′2= 2 的直径,直线l′过原点O′,因此直线l也过原点O,即直线l经过定点(0,0).

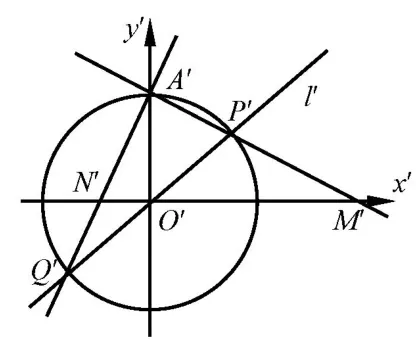
图3

(三)割线定理

例4(2018年高考天津卷文科第19 题)设椭圆的右顶点为A,上顶点为B.已知椭圆的离心率为

(1)求椭圆C的方程;

(2)设直线l:y=kx(k <0)与椭圆交于P,Q两点,l与直线AB交于点M,且点P,M均在第四象限.若∆BPM的面积是∆BPQ面积的2 倍,求k的值.

解析第(1)问略,下面考虑第(2)问.

图4

因为A(3,0),B(0,2),所以A′(3,0),B′(0,3),|A′B′|=因 为S∆BPM= 2S∆BPQ,所以S∆B′P′M′=2S∆B′P′Q′,|P′M′|= 2|P′Q′|= 2×2×3 = 12,|M′Q′|=|P′Q′|+|P′M′|=6+12=18.

因为M′是圆x′2+y′2= 9 外一点,所以|M′A′| ·|M′B′|=|M′P′| · |M′Q′|= 12×18 = 216,|M′A′| ·

因为 直线A′B′的方程为y′=−x′+3 且M′点在直线A′B′上,M′点在第四象限,所以所以

(四)相交弦定理

例5(2019年高考全国Ⅰ卷理科第10 题)已知椭圆C的焦点为F1(−1,0),F2(1,0),过F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( ).

解析设椭圆C的方程为=1(a>b>0),如图5.

由椭圆定义得:|BF1|+|BF2|=2a=|AF2|+|AF1|,因为|AF2|=2|BF2|,所以|BF1|+|BF2|=2|BF2|+|AF1|,|BF1|=|BF2|+|AF1|.

又因为|AB|=|AF2|+|BF2|=|BF1|,所以|AF1|=|AF2|,A为椭圆的上顶点或下顶点,不妨取上顶点A(0,b).

图5

图6

对椭圆C实施变换得到圆x′2+y′2=a2,如图6.

A(0,b),B分别对应变为A′(0,a),B′.因为F1,F2均在x轴上,所以 实施变换后F1,F2坐标保持不变,即F1(−1,0),F2(1,0),|A′F2|2=|A′O′|2+|O′F2|2=a2+1.

设|B′F2|=x,则|A′F2|= 2|B′F2|= 2x,所以|A′F2|2=4x2=a2+1.又因为

所以4x2= 2(a2−1),a2+1 = 2(a2−1)= 2a2−2,a2= 3,b2=a2−1 = 3−1 = 2,故椭圆C的方程为

例6(2018年高考浙江卷第17 题)已知点P(0,1),椭圆=m(m>1)上两点A,B满足则当m=____时,点B横坐标的绝对值最大.

解析对椭圆实施变换φ:得到圆x′2+y′2=4m(m>1),如图7.

A,B,P(0,1)分别对应变 为A′,B′,P′(0,2),所以|B′P′|2=2m −2.

设B′(x0,y0),则|B′P′|2=x02+(y0−2)2=2m −2.因为B′点在x′2+y′2=4m(m>1)上,所以x02+y02=4m.

图7