有限群的广义c#-正规子群

韦华全，袁卫峰，周宇珍，李 雪，李 敏

(1.广西大学 数学与信息科学学院, 广西 南宁 530004；2.广西大学 教务处, 广西 南宁 530004)

本文所有的群都是有限群，以π(G)表示群G的阶|G|的所有素因子的集合，M<·G表示M是G的极大子群，Hallπ(G)表示G的Hallπ-子群的集合。

正规子群是群论最基本的概念之一，它对群论的研究起到非常重要的作用。正规概念有多个重要推广，相应地也得到了丰富的研究成果,如：Gaschütz[1]于1962年提出了覆盖-远离子群(CAP-子群)的概念;后来有许多学者用子群的覆盖-远离性研究群的结构，给出了可解群、p-幂零群、超可解群和局部定义群系的一些充分或必要条件，见文献[2-6]；Wang[7]于1996年引入了c-正规子群的概念，并成功利用极大子群、Sylow子群的极大子群等的c-正规性，得到有限群可解、超可解的若干判别准则；2006年，韦华全[8]引入c#-正规性与c#-可补性，并利用某些极大子群、2-极大子群和Hall子群的c#-正规性与c#-可补性，得到了有限群可解(或π-可解)的充分或必要条件，统一推广了若干有关覆盖-远离性、c-正规性与c-可补性的熟知结果(亦可参见文献[9-10])。关于c-正规概念的其他推广以及利用子群的其他特性研究可解群的结果，读者可参看文献[11-20]。

本文引入广义c#-正规子群, 它是覆盖-远离子群和c-正规子群的另一种统一推广。首先，利用Hall子群的广义c#-正规性，得到有限群π-可解的一个充要条件，推广了Schur-Zassenhaus定理；其次，利用可解Hall子群和Sylowp-子群的极大子群的广义c#-正规性，得到有限群可解的两个充分条件；最后，利用可解极大或2-极大子群的广义c#-正规性，得到有限群可解的2个充要条件。

1 定义及引理

定义1[2]设A是群G的子群，H/K为G的主因子。若HA=KA，则称A覆盖H/K；若H∩A=K∩A，则称A远离H/K；若A或覆盖或远离G的每个主因子，则称A为G的CAP-子群。

定义2[7]设G是群，H为G的子群。称H为G的c-正规子群，如果存在G的正规子群K，使得G=HK且H∩K≤HG，其中HG是G的含于H的最大正规子群。

下面引入广义c#-正规子群。

定义3设G是群，H为G的子群。称H为G的广义c#-正规子群，如果存在G的正规子群K，使得HK在G中正规，并且H∩K是G的CAP-子群。

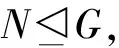
① 如果N≤H，那么H/N为G/N的广义c#-正规子群；

② 如果gcd(|H|,|N|)=1，那么HN/N为G/N的广义c#-正规子群。

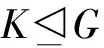
① 当N≤H时，H/N∩KN/N=(H∩K)N/N是G/N的CAP-子群，所以H/N为G/N的广义c#-正规子群。

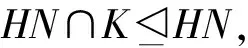
类似可证N∩(HN∩K)=N∩K∈Hallπ′(HN∩K)。因此HN∩K=(H∩K)(N∩K)，(HN∩K)N/N=(H∩K)N/N，(H∩K)N/N是G/N的CAP-子群，故HN/N为G/N的广义c#-正规子群。证毕。

以下Thompson定理见文献[21]。

引理2[21](Thompson定理) 存在奇阶幂零极大子群的群可解。

引理3[8]群G可解当且仅当存在G的可解c#-正规极大子群M。

引理4(Burnsidep-幂零准则) 设G是群,P∈Sylp(G)。若NG(P)=CG(P)，则G为p-幂零群。

引理5[8]群G可解当且仅当存在G的可解c#-正规2-极大子群L。

2 主要结果

定理1设H是群G的Hallπ-子群，其中π是一个素数集合，则G是π-可解群或π′-可解群当且仅当H为G的广义c#-正规子群。

证明必要性。设G是π-可解群。则对G的任意主因子A/B，A/B为π′-群或p-群，其中p∈π。若前者成立，则A/B∩HB/B=1，H∩A=H∩B，即H远离A/B；若后者成立，则A/B≤HB/B，于是HA=HB，即H覆盖A/B。故H为G的CAP-子群，H是G的广义c#-正规子群。同理可证，当G是π′-可解群时，H也是G的广义c#-正规子群。

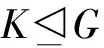
情形1若2∉π，则G是π-可解群。

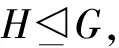
情形2若2∈π，则G是π′-可解群。

设K≠1，N是G的极小正规子群且N≤K。若HG≠1，利用归纳法，G/HG是π′-可解群，所以G是π′-可解的。若HG=1，则H∩K必定远离N/1，故(H∩K)∩N=H∩N=1，N是π′-群。由奇阶定理得N可解。再由引理1②及归纳法知G/N是π′-可解，故G是π′-可解群。证毕。

推论1(Schur-Zassenhaus定理的推广) 设H是群G的Hallπ-子群，其中π是一个素数集合。若H为G的广义c#-正规子群，则H在G中有补且所有这样的补在G中共轭。

推论2设P是群G的Sylowp-子群，其中p∈π(G)，则G是p-可解群当且仅当P在G中广义c#-正规。

证明因2′-可解群必是可解群，由定理1及其证明即得结论。

定理2设H1和H2是群G的2个可解子群，使得G=H1H2。如果H1是G的广义c#-正规Hall子群，那么G是可解群。

gcd(|H2:H1∩H2|,|H1∩H2|)=gcd(|G:H1|,|H1∩H2|)=1，

所以H1∩H2是H2的Hall子群。设π=π(H1∩H2)并设(H2)π′是H2的Hallπ′-子群，那么H2=(H1∩H2)(H2)π′，且G=H1(H2)π′。下面考虑K1的2种情形：

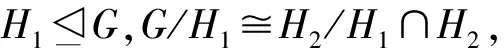
② 若K1≠1，设N是G的含于K1的极小正规子群。若H1∩K1覆盖N/1，则(H1∩K1)N=H1∩K1，因此，N≤H1，N可解。由引理1①，H1/N是G/N的广义c#-正规可解Hall子群。又G=(H1/N)(H2N/N)，利用归纳法，G/N可解，这样G可解。如果H1∩K1远离N/1，则H1∩N=1，N是σ′-子群，其中σ=π(H1)。进一步由G=H1(H2)π′可得N≤(H2)π′≤H2，所以N可解。类似可证G可解。证毕。

定理3设H是群G的Sylowp-子群的极大子群，其中p∈π(G)且gcd(|G|,p-1)=1。如果H是G的广义c#-正规子群，那么G是可解群。

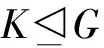
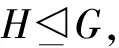
(HN/N)∩(K/N)=(H∩K)N/N

是G/N的CAP-子群。这表明，HN/N是G/N的广义c#-正规子群。由推论2，G/N是2-可解群，当然，G/N可解。最后由N可解得G可解。证毕。

推论3设M是群G的幂零极大子群，P是M的Sylow 2-子群。若P或P的某个极大子群为G的广义c#-正规子群，则G可解。

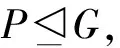
定理4群G可解当且仅当存在G的可解广义c#-正规极大子群M。

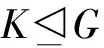
定理5群G可解当且仅当存在G的可解广义c#-正规2-极大子群T。

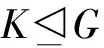
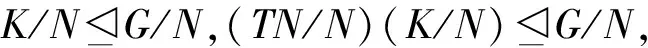
注2上述定理是利用子群的广义c#-正规性得到的结果，换成更强的“c-正规性”，则结论中的必要性未必成立；或者由于过强的条件不能满足而无法直接用“c-正规性”去判别群的(π-)可解性。

例如, 设G=S4为4次对称群,P是G的Sylow 3-子群，则K4故P是G的广义c#-正规子群，这里A4为4次交错群，K4是Klein四元群。但P不是可解群G的c-正规子群。若不然，存在使得G=PK且P∩K=1，这样K是G的正规Sylow 2-子群，矛盾。这表明，将广义c#-正规换成c-正规，定理1结论中的必要性是不成立的，而由于条件过强常常得不到满足，所以定理2或定理5换成“c-正规性”条件也不实用。

又如，设P=〈a,b|a3=b3=[a,b]=1〉,c∈Aut(P)，且满足c-1ac=b-1,c-1bc=a。则o(c)=4。令G=P〈c〉并取H=〈c2〉。易知,H<·〈c〉，且故H是G的广义c#-正规。由定理3或定理5可以判别G是可解群。但是,H不是G的c-正规子群。若不然，存在使得G=HK且H∩K=1 (因HG=1), 进而, 〈c〉=H(〈c〉∩K)=〈c〉∩K，〈c〉≤K，导致H=H∩K=1，矛盾。