一类三点共线问题的解析与探究

广东省汕头市潮南区砺青中学(515135) 郑灿基

江苏省淮安市范集中学(223215) 胡传虎

一、问题呈现

(2019年山东枣庄市高二期末)已知圆O:x2+y2=1,点P在直线l:y=x+2 上,若圆O上存在两点A,B,使得则点P的横坐标的取值范围是( )

本题以直线和圆为背景,以向量为载体,涉及三点共线问题,着重考查逻辑推理、数学运算等核心素养,需要运用数形结合、转化与化归等思想方法进行解题.本题看似较为平淡,实则是一道内涵丰富的好题.

二、思路分析及解答过程

本题由已知条件可以得出直线l与圆O相离,题设目标是求满足的点P的横坐标的范围,需围绕点P寻找条件,建立关于点P的关系式或不等式.本题对于不少学生而言是陌生的,P,A,B虽三点共线,但涉及的动点较多,感觉入手困难,需挖掘题目中隐含条件.

1 几何视角

根据题目条件,数形结合,注重挖掘其中的几何性质.

解析连结OP,设直线OP与圆O相交于C,D两点.如图1 所示.由得因为PD≤PB,PC≥PA,所以要使得圆O上存在两点A,B,使得必须满足所以(r为圆O的半径)即PO≤2r.设P(x0,x0+2),则解得−2≤x0≤0.

2 代数视角

解析设P(x0,x0+2),A(cosα,sinα),B(cosβ,sinβ)(α≠β),可由得

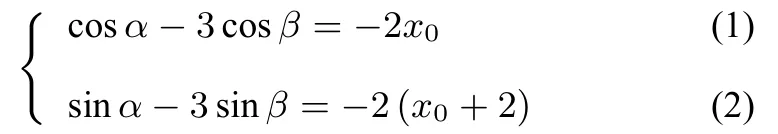
由(1)2+(2)2得10−6 cos(α−β)=4x02+4(x0+2)2.

由0≤α＜2π,0≤β＜2π知α−β ∈(−2π,0)∪(0,2π),所以−1≤cos(α−β)＜1,所以4＜10−6 cos(α−β)≤16,即4＜4x02+4(x0+2)2≤16,解得−2≤x0≤0.

点评解法1 注重挖掘图形的几何性质,等价转化为是解题的关键,有利于培养学生的几何直观能力;解法2 实质上是常规解法,利用设点P的坐标建立关于横坐标x0的关系式,利用三角函数的性质建立关于x0的不等式,进而求得x0的取值范围,有利于培养学生的化归和运算能力.

三、问题拓展和探究

解析几何试题常隐藏一些几何或代数背景,需要去深入挖掘.试题当然是以具体的数据呈现出来的,但若有序地改变条件,进行追问探究,往往可得到意想不到的发现.

对于本问题,可以尝试改变点P的位置和λ的取值来进行探究.

性质1已知圆O:x2+y2=r2,点P(x0,y0)在圆O外,如果圆O上存在两点A,B,使得(λ＞0 且1),则点P应满足

证明使用几何视角探究.由得

图2

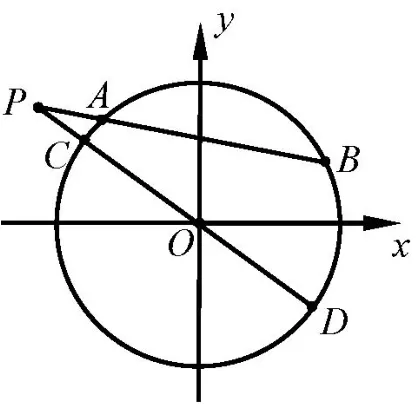
图3

①当λ＞1 时,如图2 所示,要使得圆O上存在两点A,B,使得需满足所以即

②当0＜λ＜1 时,如图3 所示,要使得圆O上存在两点A,B,使得需满足所以即

综上所述,要使圆O上存在两点A,B使得动点P需满足

性质2已知圆O:x2+y2=r2,点P(x0,y0)在圆O内,如果圆O上存在两点A,B,使得(λ＜0),则点P应满足

证明仍使用几何视角探究.由得

①当−1≤λ＜0 时,如图4 所示,要使得圆O上存在两点A,B,使得需满足所以(r为圆O的半径)即

图4

图5

②当λ＜−1 时,如图5 所示,要使得圆O上存在两点A,B,使得需满足所以(r为圆O的半径)即

综上所述,要使圆O上存在两点A,B,使得动点P需满足

事实上,通过上述探究过程,可以得到一般性结论:

已知圆M:(x−a)2+(y−b)2=r2,点P的坐标为(x0,y0),如果圆M上存在两点A,B,使得那么

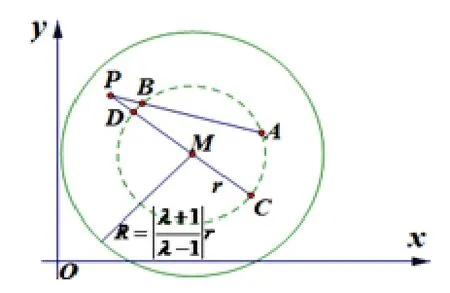
图6

图7

①当λ＞0 且1 时,必须满足r＜|PM|≤可以看出点P的轨迹是以点M为圆心,内半径为r,外半径为的圆环内所有点(包含外圆上的点,不包括内圆上的点).

②当λ＜0 时,必须满足可以看出点P的轨迹是以点M为圆心,外半径为r,内半径为的圆环内所有点(包含内圆上的点,不包括外圆上的点).

四、进一步研究——类比迁移

由于椭圆和圆在方程的结构、图形上有高度的相仿性,笔者猜想在椭圆里也应有类似的性质和结论.

性质3已知椭圆=1(a＞b＞0),点P(x0,y0),若椭圆C上存在两点A,B使得则

(i)当λ＞0 且1 时,点P在椭圆C外,且满足

(ii)当λ＜0 时,P(x0,y0)在椭圆C内,且

证明尝试利用代数视角探究.设

bsinα−λbsinβ=(1−λ)y0,即

①2+②2得因为0≤α＜2π,0≤β＜2π,所 以α−β ∈(−2π,0)∪(0,2π),所以−1≤cos(α−β)＜1.

当λ＞0 且λ1 时,P(x0,y0)在椭圆C外.因为(1−λ)2＜1−2λcos(α−β)+λ2≤(1+λ)2,所以(1−λ)2＜(1−λ)2即

当λ＜0 时,P(x0,y0)在椭圆C内.因为(1+λ)2≤1−2λcos(α−β)+λ2＜(1−λ)2,所 以(1+λ)2≤(1−λ)2

于是,在椭圆中可以得到一般性结论:

①当λ＞0 且1 时,如图8,P(x0,y0)在椭圆C外,且从而点P的轨迹是在内椭圆C与外椭圆之间(含外椭圆C′,不含内椭圆C)的所有点.

图8

②当λ＜0 时,如图9,P(x0,y0)在椭圆C内,且从而点P的轨迹是在内椭圆与外椭圆C之间(含内椭圆C′,不含外椭圆C)的所有点.

图9

五、模拟训练,举一反三

基于以上认识和探究得到的结论,笔者设计下列两道试题,供读者参考.

变式1已知圆C1:x2+(y−3)2=1,点P是抛物线C2:y=x2上一点,若圆C1上存在两点A,B,使得求点P的横坐标的取值范围.

(提示:设P(x0,x02),利 用即|C1P|≤3 建立不等式,可得)

变式2已知椭圆点P是圆C2:x2+(y−2)2=8 上一点,若椭圆C1上存在两点A,B,使得求点P的纵坐标的取值范围.

(提示:设P(x0,y0),利用即2＜x02+2y02≤8 并结合x◦2+(y◦−2)2=8,可求得

六、对本文的总结

波利亚说过:“解题就像采蘑菇一样,当我们发现一个蘑菇时,它的周围可能有一个蘑菇圈.”通过对本试题的深入观察,多向思维,巧妙拓展,看似平常的一道直线与圆的求解问题,却独具匠心.在实际解题教学中,教师应努力寻找好题,引导学生探究,通过一题多解和变式拓展等环节,不仅可以让学生体验到数学再创造的思维过程,而且可以培养学生的创新意识和科学精神.教师在解题教学中要善于引导学生抓住问题的本质,在千变万化的题目中寻找不变的规律,只有这样才能够提高学生的学习效率,达到事半功倍的效果.