一类恶意蠕虫和良性蠕虫的交互传播模型研究*
陈 迪,赖际颖,高淑京
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
1 引言
随着计算机网络的广泛应用,非法访问、恶意蠕虫攻击和计算机病毒等网络安全问题,变得越来越突出.网络蠕虫是一种恶意代码,它不需要人类的干预,即可自动运行并通过网络进行自我复制并传播.如KoobFace蠕虫[1],它针对的是Facebook、Gmail等社交网站的用户,用户的设备被感染后,会泄露用户的个人数据、密码以及金融服务信息.网络蠕虫造成的危害比其他网络安全威胁更大,因此,如何抑制网络蠕虫在网络中大规模的传播是一个迫切需要解决的问题.
Castaneda等人[2]最早提出了一种“以毒攻毒”思想即将恶意蠕虫转化为良性蠕虫,利用良性蠕虫抑制恶意蠕虫的传播.良性蠕虫融合了密码学、网络攻击和计算机病毒等技术,网络蠕虫一样可以进行自我复制,不需要用户干预即可自动运行,是一种智能的、自动化的攻击程序或代码.良性蠕虫已被证实可以有效的检测并清除恶意蠕虫,已成为一种新的网络安全应对措施[3].随着主动良性蠕虫和被动良性蠕虫的发展,文献[4]将良性蠕虫分成主动良性蠕虫、被动良性蠕虫,以及混合良性蠕虫,并建立了简单混合良性蠕虫模型,该混合良性蠕虫在主动探测漏洞主机的同时也在被动监听恶意蠕虫的攻击.作者通过数值模拟,将混合良性蠕虫与主动、被动良性蠕虫进行了对比,验证了混合良性蠕虫的有效性.许多学者还提出“分而治之”的混合良性蠕虫[5-6],将主动良性蠕虫和被动良性蠕虫的优点结合,在恶意蠕虫达到一定数量时进行切换,使其在初级阶段主动攻击恶意蠕虫和恶意感染主机,中后期被动监听恶意蠕虫的攻击,使混合良性蠕虫能有效控制恶意蠕虫的同时,减少在对抗后期产生的额外网络流量,不占用网络其他资源.考虑到混合良性蠕虫的有效性,并且以上模型都没有进行动力学分析,本文提出了恶意蠕虫和混合良性蠕虫的交互传播模型,并进行动力学分析.
2 模型与假设
我们把计算机看成节点,所有的节点分为四类:易感类节点,感染恶意蠕虫的节点,感染良性蠕虫的节点,免疫类节点.令S(t),I(t),B(t),R(t)分别表示易感节点,恶意蠕虫节点,良性蠕虫感染节点,免疫节点的比率.记N(t)=S(t)+I(t)+B(t)+R(t),不失一般性N(t)≡1.
为了建立该模型,我们提出以下假设:
(H1)网络中只存在两类蠕虫:恶意的网络蠕虫和混合良性蠕虫;
(H2)所有蠕虫采取随机扫描策略;
(H3)良性蠕虫本身对恶意蠕虫具有免疫性;
(H4)混合良性蠕虫具有主动修补易感节点,清除感染节点的蠕虫,被动监听节点,等待恶意蠕虫攻击等功能[4].
令μ表示新入网的计算机的比率和计算机报废的比率;β1表示被恶意蠕虫成功扫描而导致的易感节点的感染率;β2表示混合良性蠕虫的感染率.模型的流程图如图1所示.
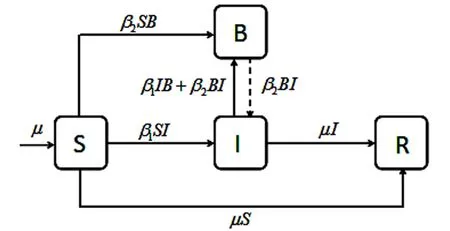
图1 恶意蠕虫和混合良性蠕虫交互传播的流程示意图(实线表示种类之间的转化,虚线表示良性蠕虫主动攻击染病主机获得传播)
我们建立如下模型:
(1)
由于模型(1)的前三个方程与免疫类“R”无关,故只需要研究系统(1)的子系统:
(2)
3 基本再生数与平衡点的稳定性
首先,我们先讨论系统(2)的平衡点.记
系统(2)有4个可能存在的非负平衡点,它们的存在条件如下:
4 平衡点的局部渐近稳定性
接下来,我们研究系统(2)的4个平衡点的局部渐近稳定性.
对任意平衡点PΔ=(SΔ,IΔ,BΔ)得系统(2)的Jacobian矩阵J(PΔ)如下:
(3)
首先,我们先讨论系统(2)无蠕虫平衡点P0的局部渐近稳定性.
将P0代入(3)得到J(P0),通过计算我们可以得到矩阵J(P0)特征方程为:(λ+γ+μ)(λ+γ+μ-β1S0)(λ+μ-β2S0)=0.因此,矩阵J(P0)对应的特征根为:
λ1=-(γ+μ),λ2=(γ+μ)(R1-1),λ3=μ(R2-1).
显然,当R1<1且R2<1时,系统(2)的无蠕虫平衡点P0是局部渐近稳定的.
同理,我们可以得到矩阵J(PΔ)在P1处的特征方程为:(λ-a2)(λ2+b2λ+c2)=0,其中a2=β1S1-β1B1-β2B1-(γ+μ),b1=β2B1+μ+γ,c1=μβ2B1.容易得到,当R3<1时,矩阵J(P1)的其中一个特征值为λ1=β1S1-β1B1-β2B1-(γ+μ)<0,其它2个特征根满足以下方程:λ2+b1λ+c1=0.当P1存在时,我们可以得到b1>0和c1>0.根据Routh-Hurwitz判据,可得λ2和λ3具有有负实部.因此,当R2>1且R3<1时,系统(2)的恶意蠕虫消失,无恶意蠕虫平衡点P1是局部渐近稳定的.

显然,当R4<1时,矩阵J(P2)的其中一个特征根为λ1=β2S2+β2I2+β1I2-μ<0,其它2个特征根满足以下方程:λ2+b2λ+c2=0.当P2存在时,我们可以得到b2>0和c2>0.根据Routh-Hurwitz判据,可得λ2和λ3具有负实部.因此,当R1>1且R4<1时,系统(2)的良性蠕虫灭绝,无良性蠕虫平衡点P2是局部渐近稳定的.
最后,将P*代入(3)得到J(P*),通过计算我们可以得到矩阵J(PΔ)在P*处的特征方程为:
λ3+a3λ2+b3λ+c3=0,
(4)
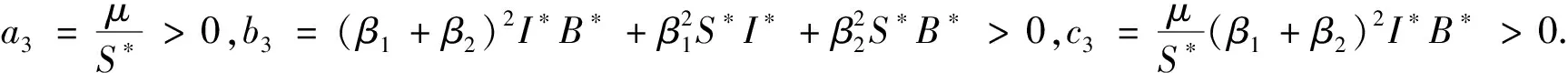
5 平衡点的全局渐近稳定性
定理1当R0<1时,系统(2)的无蠕虫平衡点P0在可行域Ω内是全局渐近稳定的.

(5)
将(5)式代入系统(2)的第二式,可以得到
[(γ+μ)(R1-1)+β1ε]I(t).
通过计算我们可以得到I(t)的解
I(t)=I(t0)exp[(γ+μ)(R1-1)+β1ε].
(6)
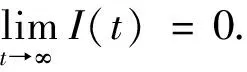
将(5)和I(t)<ε代入系统(2)中的第三式

由此我们可以得到,当R0<1时,系统(2)的无蠕虫平衡点P0在可行域Ω内是全局渐近稳定的.
定理2当R2>1且R3≤1时,无恶意蠕虫平衡点P1在可行域Ω{P0}内是全局渐近稳定的.
证明当R2>1时,可以看出系统(2)有无恶意蠕虫平衡点P1,构造以下Lyapunov函数:
(7)
则V1沿着模型(2)的解曲线的全导数为

根据LaSalle不变集原理,系统(2)从Ω{P0}内出发的解都趋于P1=(S1,0,B1).所以当R2>1且R3≤1时,无恶意蠕虫平衡点P1在可行域Ω{P0}内是全局渐近稳定的.
定理3当R1>1且R4≤1时,无恶意蠕虫平衡点P1在可行域Ω{P0}内是全局稳定的.
证明当R1>1时,可以看出系统(2)有无良性蠕虫平衡点P2,构造以下Lyapunov函数:
(8)
则V2沿着模型(2)的解曲线的全导数为

根据LaSalle不变集原理,系统(2)从Ω{P0}内出发的解都趋于P2=(S2,I2,0).所以当R1>1且R4≤1时,无恶意蠕虫平衡点P2在可行域Ω{P0}内是全局渐近稳定的.
定理4当R3>1且R4>1时,正平衡点P*在可行域Ω{P0}内是全局渐近稳定的.
证明当R3>1且R4>1时,可以看出系统(2)有正平衡点P*,构造以下Lyapunov函数:
则V3沿着模型(2)的解曲线的全导数为
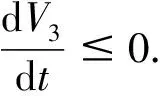
根据LaSalle不变集原理,系统(2)从Ω{P0}内出发的解都趋于P*=(S*,I*,B*).所以当R3>1且R4>1时,正平衡点P*在可行域Ω{P0}内是全局渐近稳定的.
6 数值模拟
我们将通过数值模拟验证理论结果.
(a)首先,我们选取参数μ=0.005,β1=0.006,β2=0.004,γ=0.005,初值条件分别为(0.4,0.1,0.5),(0.2,0.5,0.3),(0.8,0.1,0.1),(0.6,0.1,0.3).计算可得P0=(0.3,0,0),基本再生数R1=0.3<1,R2=0.4<1.图2所示,经过不同初值的解曲线,最终趋近于无蠕虫平衡点.

图2 当R1=0.3<1,R2=0.4<1时,系统(2)的无蠕虫平衡点的稳定性.
(b)我们选定参数μ=0.000 4,β1=0.000 5,β2=0.000 8,γ=0.000 2,初值条件分别为(0.6,0.15,0.25),(0.1,0.2,0.7),(0.3,0.5,0.2),(0.4,0.3,0.3).计算可得P1=(0.8,0,0.25),基本再生数R2=1.333>1,R3=0.480 4<1.图3所示,经过不同初值的解曲线,最终趋近无恶意蠕虫平衡点.
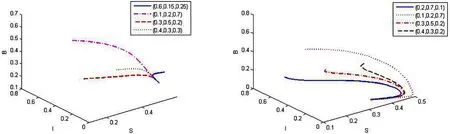
图3 当R2=1.333>1,R3=0.480 4<1时,系统(2)无恶意蠕虫平衡点的全局稳定性. 图4 当R1=1.375>1,R4=0.95<1,系统(2)无良性蠕虫平衡点的全局稳定性.
(c)我们选定参数μ=0.01,β1=0.055,β2=0.002,γ=0.01,初值条件分别为(0.1,0.2,0.7),(0.3,0.5,0.2),(0.4,0.3,0.3),(0.4,0.3,0.3).计算可得P2=(0.363 6,0.136 4,0),基本再生数R1=1.375>1,R4=0.95<1.图4所示,经过不同初值的解曲线,最终趋近无良性蠕虫边界平衡点.
(d)我们选定参数μ=0.001 8,β1=0.004 6,β2=0.002,γ=0.000 1,初值条件分别为(0.1,0.1,0.8),(0.3,0.2,0.5),(0.1,0.7,0.2),(0.6,0.3,0.1).计算可得P*=(0.698,0.061 2,0.198 6),基本再生数R3=1.289 4>1,R4=1.689 9>1.图5所示,经过不同初值的解曲线,最终趋近正平衡点.

图5 当R3=1.289 4>1,R4=1.689 9>1,系统(2)的正平衡点的全局稳定性. 图6 不同的参数μ对恶意主机I(t)的数量的影响.
接下来,我们研究参数对蠕虫传播的影响.
(e)我们选定参数β1=0.006,β2=0.004,γ=0.000 5,比较不同的参数μ=0.002,0.005,0.007,对恶意主机数量的影响.从图6可看出,适当增大μ的大小可以控制恶意蠕虫的传播.
(f)我们选定参数μ=0.01,β1=0.05,γ=0.01,比较不同的参数β2=0.002,0.004,0.006,对恶意主机和良心感染主机的数量的影响.从图7可看出,增大β2的大小,可以减少恶意蠕虫的数量,并使良性感染主机数量增加.

图7 不同的感染率β2,对系统(2)中I(t)和B(t)的数量.
7 控制措施
根据数值模拟结果,我们提出以下建议:

