11阶幻方与等幂和
张在明
(玉溪师范学院,云南 玉溪 653100)
本文介绍两个漂亮的11阶完美对称幻方(图1、图2)以及依托这两个幻方而得到的等幂和数组和代数恒等式.

图1 11阶完美·对称 幻方(1) 图2 11阶完美·对称 幻方(2)
首先说明图中的幻方都是完美幻方.显然可以直接计算出其行、列、左、右泛角线的数字和均为671.不过下面再介绍一种通用的方法,即自然数阵的数字结构特点,以此建立自然数阵与幻方的内在联系,为节省篇幅而又不失一般性,不妨以7阶为例.
先看7阶自然数阵(图3),其中心位置的数字为25,左对角线上的数字依序为:1、9、17、25、33、41、49,组成公差为8的等差数列,中项为25,左、右数字以25为对称中心,其和为175.
现在列表讨论左泛角线数字特点(图4),第2行前6个数字比第1行增1,共增加6,最后数43恰比49减少6,第2行的数字和仍为175.右泛角线7组数字也是如此,加上第4行、第4列(对称1),于是便首先凑够7阶幻方中7行7列,二主对角线的全部16组数.接下来的任务便是把自然数阵的此16组数字构造为7阶幻方,7阶对称幻方乃至7阶完美对称幻方,这些就是文献[1]所讨论的问题.

图3 7阶自然数阵 图4 左泛角线数字特点
以下演示通过7阶自然数阵,用铺地锦加斜排(一定要跳空一格!)构造两个7阶完美对称幻方(图5):

图5 用铺地锦加斜排构造7阶完美对称幻方

图6 7阶完美对称幻方(1) 图7 7阶完美对称幻方(2)
简要过程:①填写自然数阵(至少一个);②以其左对角线数组为准,成为7阶完美对称幻方的第4行;③以1为起点,跳一格斜排向上向下取点列20、32、44以及38、26、14,共7个数字组成7阶完美对称幻方的第1列;④如图5所示,相继完成幻方的其他6行的数组.⑤见图6,完成第1个7阶完美对称幻方的构造过程;⑥验证图6中的7阶数阵,确是幻方,对称幻方,完美幻方(从略);⑦仿此,以自然数阵右对角线为依据,构造另一个7阶完美对称幻方)(过程从略,结果由图7显示).
把7阶自然数阵换成11阶,用铺地锦加斜排(跳空一格),如法类推便得到图1、图2中的两个11阶完美对称幻方.
由于10进位制的关系,此二幻方数字安排特别漂亮,尤其是图1,故笔者将它命名为“Forget me not!”(毋忘我),它有下面几个特点:
①第6行从左到右,组成以10为公差的等差数列,末位数字均为1,简明,标准,第5行乃由11阶自然数阵中的右对角线演变而来.
②第3行也很有意味,中间数字121为最大数,犹如中流砥柱,巍然屹立.左右10个数,从10、20到90、100,这正是10进位数独有的魅力,为别的幻方所缺失.
③第1、2、4、5行都是两组公差也是10的等差数列组成,条理分明,都是由自然数阵中的右泛对角线数组构成.
④与之相对称的是第6行到第11行,交相辉映,如121与1,一高一低,一大一小,遥相呼应.
⑤幻方中的数字还具有奇偶分开的特点.
⑥对泛对角线数字和的验证,同样可用以左右对角线数字相对比进行,比如左对角线与相邻一组右泛对线,由下可见增减一样,其和不变:
2、16、30、44、47、61、75、78、92、106、120
9、12、26、40、54、57、71、85、99、102、116
(7、-4、-4、-4、7、-4、-4、7、7、-4、-4)
至于图2中的11阶完美对称幻方,可视为图1中的幻方的伴随幻方,异中有同,同中有异.
以下,讨论依托这两个幻方而构建的等幂和恒等式,有别于一般资料的方法,本文将采用一般化的表现形式.为此,必须对幻方作“对称化”的技术处理(将各数字减去61,再一一加上未知元y,如图8所示.)

图8 对幻方作“对称化”技术处理
先讨论第1行,其数字的2次等幂和,有
(y-49)2+(y-28)2+(y-18)2+(y-8)2+(y+2)2+(y+12)2+(y+22)2+(y+32)2+
(y+42)2+(y+52)2+(y-59)2=
11y2+2(-49-28-18-8+2+12+22+32+42+52-59)y+492+282+182+82+22+
122+222+322+422+522+592=11y2+0y+13 178=11(y2+1 198)
由于对称性,不难发现,第11行诸数字的2次等幂和也等于11(y2+1 198).
同样的讨论适合第1列与第11列,有
(y-49)2+(y-25)2+(y-1)2+(y+23)2+(y+47)2+(y-50)2+(y-37)2+(y-13)2+
(y+11)2+(y+35)2+(y+59)2=
11y2+492+252+12+232+472+502+372+132+112+352+592=11(y2+1 330)

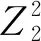
(y-25)2+(y+9)2+(y+43)2+(y-44)2+(y-10)2+(y+24)2+(y+58)2+(y-29)2+
(y+5)2+(y+28)2+(y-59)2=11y2+13 662=11(y2+1 242)


经过一番计算,关系到图8中11阶完美对称幻方一般式的行、列、左(右)泛对角线的2次等幂和代数恒等式,用简单符号表示共得




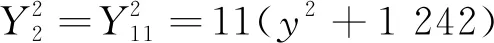

否则,只得另辟蹊径!
再说图2中幻方所涉及的2次等幂和问题.不难断定,其行(列)相关的等式与图1中的毫无二致,仅数字排序不同,至于左(右)泛对角线方面的,则有所不同,举二例于下:
还有3次等幂和式必须列出:
在上面的2次、3次等幂和等式中,取y=61,便得到文章开头部分,即图1、图2,两个11阶完美对称幻方所依托的等幂和等式,举4例于下:
602+702+802+902+1002+1212+102+202+302+402+502=
722+822+922+1022+1122+12+222+322+422+522+622=
11(3 721+1 110)=53 141
332+462+702+942+1182+212+342+582+822+1062+92=
1132+162+402+642+882+1012+42+282+522+762+892=
11(3 721+1 176)=53 867
123+463+803+1143+273+613+953+83+423+763+1103=
23+163+303+443+473+613+753+783+923+1063+1203=
11×61(3 721+6×632)=5 041 223
223+543+863+1183+293+613+933+43+363+683+1003=
1113+1043+963+883+693+613+533+343+263+183+103=
11×61(3 721+6×588)=4 864 079

