一段美丽的邂逅：当“存在”遇到“任意”

浙江省温州中学 (325000) 吴时月

当代数学教育家弗赖登塔尔曾经指出：“反思是数学活动的核心和动力”，可见反思的重要性. 老师不仅要让学生知道解后反思的内容和重点，更要教会学生如何反思. 通过解题反思，引导学生再次对问题进行分析、对比、归纳与总结，对问题中所蕴含的数学思想方法进行再审视，起到一个再提高的作用.

笔者在高三复习“函数中的存在与任意问题”时，遇到了这样一道题：

已知函数f(x)=x2+(a-4)x+3-a，若对于任意的a∈(0,4)，存在x∈[0,2]，使得|f(x)|≥t，求t的取值范围．

课堂期间同学们提出的问题与想法引发了笔者的思考．以下便是学生与笔者对这道题的分析与讲评实录.

学生1：通过观察发现函数f(x)=x2+(a-4)x+3-a既是关于x的二次函数，又是关于a的一次函数，采用主元法的思想将f视为a的一次函数得：f(x)=F(a)=(x-1)a+x2-4x+3=(x-1)(a+x-3)，且a=3-x∈[1,3]⊆[0,4].所以|F(a)|min=|(x-1)a+x2-4x+3|min=|F(a=3-x)|=0，所以t≤0.

师：学生1很有自己的想法，主次元换位，一次主导，避开了分类讨论，那该解法是否正确呢？ 最终答案是否正确呢？

学生2：将函数f(x)=x2+(a-4)x+3-a视成x的二次函数，按对称轴进行分类：

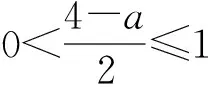
师：与同学1的切入角度不一样，生2将f(x)视成x的二次函数.按照对二次函数的对称轴进行严格的分类讨论来解决经典的含参问题，但是以上两种处理手法带来的答案是不一样的，到底哪个正确呢？

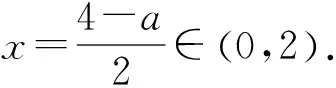
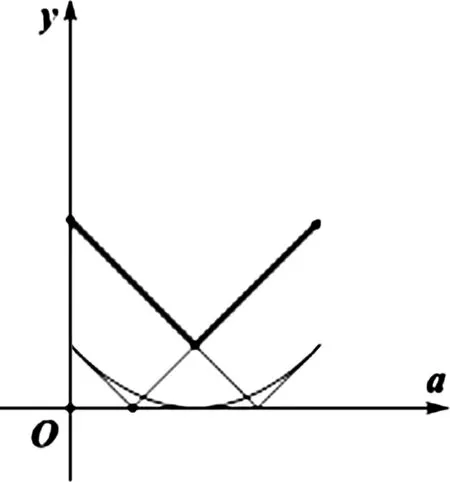
图1

=g(a)，如图1，通过比较易知g(a)=

师：因为对称轴范围的特殊性，直接比较两个端点及对称处的函数值的绝对值的大小，是学生2的解法的升级版.

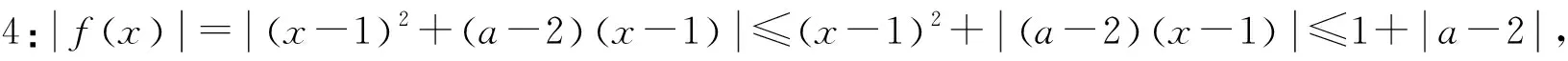
师：主导思想还是先视x为主元，结合x的取值特点，以非常巧妙的放缩的方式来解决问题，同时保证等号同时取到，令人耳目一新！

师：解法1中已发现原函数具有因式分解的效果，与解法1不同的是解法5仍是以x为主元，两个一次函数的绝对值同时取到最大值，解法非常新颖．

对比以上几种解法，最大的分歧在于先以哪个参数为主元．到底哪种理解正确呢？我们有必要一探究竟．为了叙述方便，我们将问题的条件重新描述如下：设二元函数F(x,a)=|x2+(a-4)x+3-a|，∀a∈(0,4)，∃x∈[0,2]，使得F(x,a)≥t.求t的取值范围.

这是一道“存在”遇到“任意”的问题．同学1的解法是先把F(x,a)看成a的函数，即先处理“任意”，再处理“存在”， 也就是将条件转化于：

同学2至5都是先把F(x,a)看成x的函数，即先处理“存在”，再处理“任意”，从而将条件转化为：

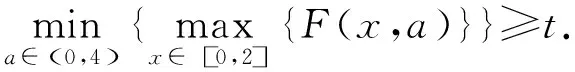
那么，此问题就归结为：“任意”与“存在”的处理次序可以随意吗？我们来回归教材，在课本【1】中，对于全称命题与特称命题的定义如下：

通常，将含有变量x的语句用p(x)表示，变量x的取值范围用M表示．那么，全称命题“对M中任意一个x，有p(x)成立”，简记为∀x∈M,p(x)，读作“对任意x属于M，有p(x)成立”．特称命题“存在M中的元素x0，使p(x0)成立”简记为∃x0∈M,p(x0)，读作“存在M中的元素x0，使p(x0)成立”．

在本问题中，对应于∀a∈(0,4)的语句p(x)应为“∃x∈[0,2]，F(x,a)≥t”．由此可见，解决该问题的逻辑顺序应为先明确语句p(x)，即先处理“存在”，然后再处理“任意”，也就是说条件应等价于：

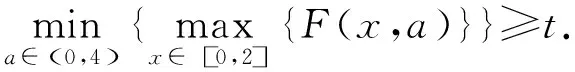
所以同学2至5的解法正确，答案正确. 而同学1的解法是以下问法的答案：F(x,a)=|x2+(a-4)x+3-a|，∃x∈[0,2]，∀a∈(0,4)，F(x,a)≥t.

于是我们可以得出如下系列结论：

图2

明确了该命题等价于求最大值的最小值后，遇上绝对值，也可以从以下角度切入：|f(x)|=|(x2-4x+3)--a(x-1)|.令g(x)=x2-4x+3,h(x)=-a(x-1)，则|f(x)|=|(x2-4x+3)-(-a(x-1))|代表两个函数g(x),h(x)的函数值之差的绝对值，如图2，由绝对值的纵向(铅锤)距离的几何意义计算可知：取a=2时，即h(x)=-2x-1时，g(x),h(x)的函数值之差的绝对值的最小为1，所以t≤1.

评注：利用的绝对值的几何意义，来寻找直(曲)线的“最佳”的位置，使得最大值最小，是非常不错的一种几何手法．

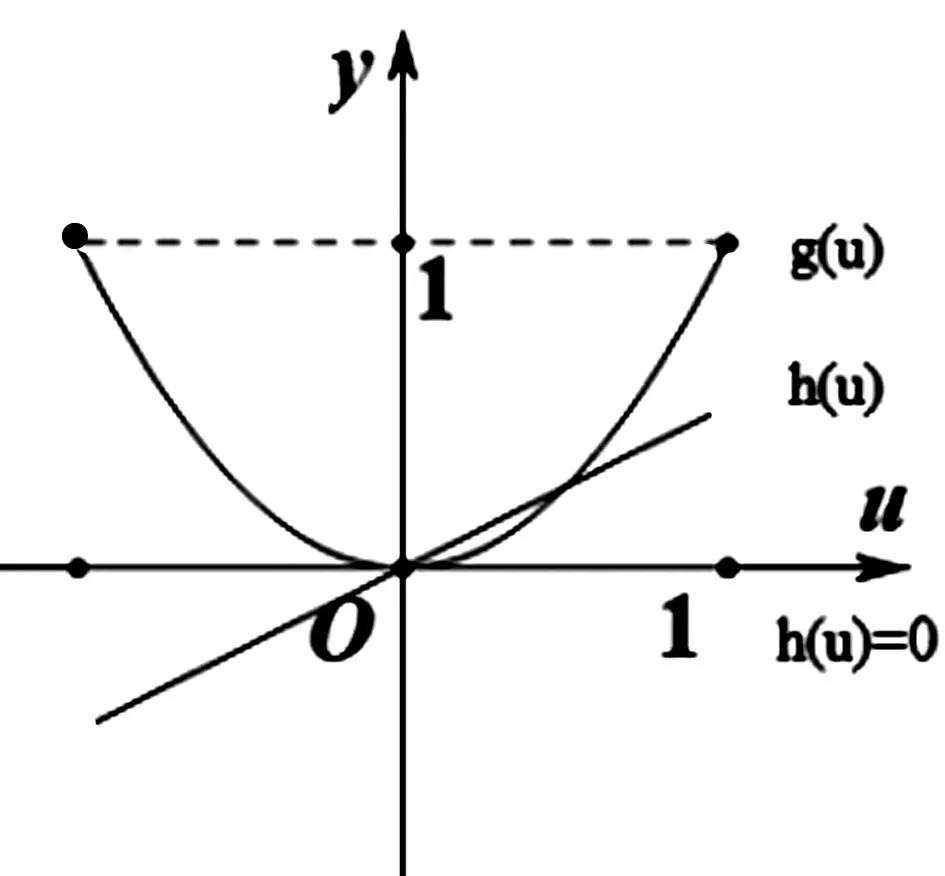
图3

评注：采用换元的方法，将原来的式子进行等价变形，简化代数式子的结构，起到事半功倍的效果.亦可理解为通过变形，把函数图象转化为类似“平口单峰”的处理形式.

学生在处理含有“存在”与“任意”等特(全)称命题时，常常会出现等价变形不到位而出错的情形.我们应该启发和引导学生先从宏观上去把握，再从微观上去突破，在解题思路的整体设计上和解题方法的优劣选择上下功夫，用研究的态度去对待我们遇到的每一个数学问题，最终对问题达成较为透彻的理解，起到揭示问题本质的作用.