SPECTRA OF COMPOSITION GROUPS ON THE WEIGHTED DIRICHLET SPACE OF THE UPPER HALF-PLANE∗
M.O.AGWANG J.O.BONYO
Department of Pure and Applied Mathematics,Maseno University,
P.O.BOX 333-40105,Maseno,Kenya
E-mail:omeshackagwang@yahoo.com;jobbonyo@maseno.ac.ke
Abstract We prove that the group of weighted composition operators induced by continuous automorphism groups of the upper half plane U is strongly continuous on the weighted Dirichlet space of U,Dα(U).Further,we investigate when they are isometries on Dα(U).In each case,we determine the semigroup properties while in the case that the induced composition group is an isometry,we apply similarity theory to determine the spectral properties of the group.
Key words one-parameter semigroup;composition operator semigroups;strong continuity;infinitesimal generator;spectra
1 Introduction
For an open subsetΩof C,let H(Ω)denotes the Fr´echet space of analytic functions onΩendowed with the topology of uniform convergence on compact subsets ofΩ.In this note,Ωcan be either the open unit disk D or the upper half plane U.Ifϕis a self analytic map onΩ,then the induced composition operatorCϕacting on H(Ω)is defined byCϕf=f◦ϕ,with the corresponding weighted composition operator on H(Ω)given bySϕ=(ϕ′)γCϕfor some appropriately chosen weightγ.
Composition operators on spaces of analytic functions on the unit disc H(D)have been extensively studied in the literature comparatively to their counterparts on the analytic spaces of the upper half plane H(U).Even though there are isomorphisms between the corresponding spaces of D and of U,composition operators act differently in the two cases.For instance,unlike the case of Hardy or Bergman spaces of D,not every composition operator is bounded on Hardy or Bergman spaces of U,see[1,2].It has also been proved in[3,4]that there are no non-trivial(i.e.with symbol not constant)compact composition operators on the Hardy spaceH2(U)or the weighted Bergman spacewhich is not the case forH2(D)or.
Unlike the Hardy and Bergman spaces of D cases,composition operators on the(weighted)Dirichlet space of the unit disk Dα(D)are not necessarily bounded;an indication that the action of composition operators on the weighted Dirichlet space of the upper half plane Dα(U)is very much complicated.Recent attempts to study composition operators on Dα(U)can be found in[5,6].Schroderus[5]obtained the spectrum of composition operators induced by linear fractional transformations(LFTs)of the upper half plane U;while Sharma,Sharma and Raj[6]characterized boundedness and compactness of composition operators on D0(U).In particular,it is proved in[6]that every LFT of U induces a bounded composition operator on D0(U).This therefore implies that continuous groups(ϕt)t∈Rof automorphisms of the upper half plane may induce a bounded group of(weighted)composition operatorsTt:=Sϕton Dα(U).It is important to note that the study of composition semigroups on the Dirichlet spaces has scantly been considered with the only reference[7]being on the Dirichlet space of the unit disk.
In this paper,we extend the study carried out by the second author with his co-authors in[8]on Hardy and weighted Bergman spaces of U to the setting of the weighted Dirichlet space of U.In particular,we prove that the group(Tt)t∈Rof weighted composition operators is strongly continuous on Dα(U).Using the classification theorem of continuous groups of automorphisms of U[8,Proposition 2.3],we consider the corresponding weighted composition operator groups(Tt)t∈Ron Dα(U)and investigate when they are isometries.It turns out that the scaling and translation groups do not induce weighted composition operator groups on Dα(U)which are isometries as is the case for Hardy and Bergman spaces of U[8].The infinitesimal generators of the composition groups are calculated and their properties discussed.For the rotation automorphism group,(Tt)t∈Rturns out to be a group of isometries on Dα(D).In this case therefore,we determine both its semigroup and spectral properties.
2 Preliminaries and Definitions


We refer to[15–17]for details on the theory of semigroups.
IfXandYare arbitrary Banach spaces,we denote the Banach space of bounded linear operators fromXtoYby L(X,Y).We shall write L(X)instead of L(X,X).LetTbe a closed operator onX.The resolvent setρ(T)ofTis given byρ(T)={λ∈C:λI−Tis invertible}and its spectrum isσ(T)=Cρ(T).The spectral radius ofTis defined byr(T)=sup{|λ|:λ∈σ(T)}and satisfies the relationr(T)≤‖T‖.The point spectrumσp(T)={λ∈C:T x=λxfor some 0≠x∈dom(T)}.Forλ∈ρ(T),the operatorR(λ,T):=(λI−T)−1is by the closed graph theorem a bounded operator onXand is called the resolvent ofTat the pointλor simply the resolvent operator.See[15,16,18]for details.
IfXandYare arbitrary Banach spaces andU∈L(X,Y)is an invertible operator,then clearly(At)t∈R⊂L(X)is a strongly continuous group if and only ifBt:=UAtU−1,t∈R,is a strongly continuous group in L(Y).In this case,if(At)t∈Rhas a generatorΓthen(Bt)t∈Rhas generator∆=UΓU−1with domain

Moreover,σp(∆,Y)=σp(Γ,X)andσ(∆,Y)=σ(Γ,X).Ifλis in the resolvent setρ(Γ,X):=Cσ(Γ,X),we have thatR(λ,∆)=UR(λ,Γ)U−1.For more details on the theory of similar semigroups,we refer to[15–17].
All self analytic maps of U were identified and classified in[8]into three distinct groups according to the location of their fixed points,namely;scaling,translation and rotation groups.Specifically we give the following classification theorem:
Theorem 2.1(see[8,Proposition 2.3])Letϕ:R→Aut(U)be a nontrivial continuous group homomorphism.Then exactly one of the following cases holds:
1.There existsk>0,k≠1,andg∈Aut(U)so thatϕt(z)=g−1(ktg(z))for allz∈U andt∈R.
2.There existsk∈R,k≠0,andg∈Aut(U)so thatϕt(z)=g−1(g(z)+kt)for allz∈U andt∈R.
3.There existsk∈R,k≠0,and a conformal mapping g of U onto D such thatϕt(z)=g−1(eiktg(z))for allz∈U andt∈R.Equivalently,there existθ∈R� andh∈Aut(U)so that:

Now from(2.2)again,we obtain
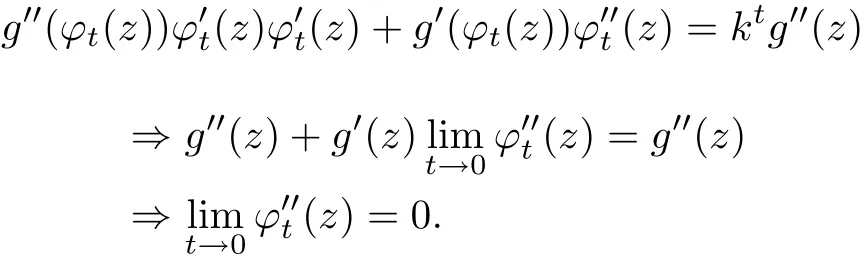
The proofs for cases 2 and 3 are similar.We omit the details.
The assertions 1,2 and 3 of Theorem 2.1 above corresponds to the automorphism groups:scaling,translation and rotation groups respectively.In this study and as noted in[8],we shall consider without loss of generality,the following special cases:
I.For the scaling group,we considerϕt(z)=e−tz,z∈U.
II.For the translation group,we considerϕt(z)=z+t,z∈U.
III.For the rotation group,we considerϕt(z)=eiktz,z∈D.
3 Scaling and Translation Groups
3.1 Strong continuity
We prove that the groups of composition operators induced by the automorphism groups I and II above are strongly continuous on the Dirichlet space of the upper half plane Dα(U).The strong continuity of composition groups on the Dirichlet space of the unit disc D was proved by Siskakis in[7].Forα>−1,let Diα(U)denotes the space consisting off∈H(U)for whichwith the norm



The RHS of equation(3.4)is not equal to the norm ‖f‖2Dα(U)for allf∈Dα(U).This implies that the weighted composition operatorTtis not an isometry on Dα(U).
Remark 3.4The fact that the weighted composition operatorTtfails to be an isometry on Dα(U)complicates the spectral analysis of the group(Tt)t∈R.This is because the theory of spectra of semigroups of linear operators are easily applied when we can identify exactly what the spectrum of(Tt)t∈Ris.For the case when(Tt)t∈Ris an isometry,then spectral mapping theorem for semigroups readily gives the spectrum of(Tt)t∈Rand together with Hille-Yosida theorem,a complete spectral analysis of the infinitesimal generator as well as the resulting resolvents can be easily carried out.For this composition group therefore,we shall only determine the point spectrum of the infinitesimal generatorΓon Dα(U),but first we state the following Lemma.
Lemma 3.5(see[8,Lemma 3.2])LetXdenote one of the spacesHp(U)orLpa(U,µα),1≤p<∞andα>−1(α=−1 ifX=Hp(U))and letγ=(α+2)/p.Ifc∈R andλ,ν∈C,then;
1.f(ω)=(ω−c)λ(ω+i)ν∈Xif and only ifℜ(λ+ν)<−γ<ℜ(λ).In particular:(ω−c)λ/∈Xfor anyλ∈C and(ω+i)ν∈Xif and only ifℜν<−γ.
2.f(ω)=eω/ωc∈Xif and only if 1/p The point spectrum of the infinitesimal generatorΓis given in the following theorem: Proposition 3.6LetΓbe the infinitesimal generator of the group(Tt)t∈Rgiven by equation(3.3).Then the point spectrum ofΓis empty,that is,σp(Γ)=∅. For the rotation group,the self-analytic maps are given byϕt(z)=eiktzforz∈D and we consider the induced groups of weighted composition operators on Dα(D)of the form for allf∈Dα(D)andc,k∈R withk≠0.Arguing as in Theorem 3.1,we see that(Sϕt)t∈Ris a strongly continuous group on Dα(D);and as we prove in the next theorem,this group is a group of isometries.LetΓc,kbe the generator of the group(Sϕt)t∈Rgiven by equation(4.1).Then as remarked in[20],to analyze the group(Sϕt)t∈R,it is sufficient to consider the case whenc=0 andk=1 since the properties are related in the following ways. Theorem 4.1Let(Sϕt)t∈Rbe a group of weighted composition operators defined on Dα(D)bySϕtf(z)=eictf(eiktz)and letΓc,kbe its infinitesimal generator.Then: 1.(Sϕt)t∈Ris an isometry on Dα(D). 2.Sϕt=Cϕtforc=0,k=1. 3.Γc,k=ic+kΓ0,1with the domain dom(Γc,k)=dom(Γ0,1)={f∈Dα(D):f′∈Dα(D)}. 4.σ(Γc,k)={ic+kσ(Γ0,1)},andσρ(Γc,k)={ic+kσρ(Γ0,1)}. 5.λ∈σ(Γ0,1)if and only if ic+kλ∈σ(Γc,k)and AcknowledgementsThe authors would like to thank the anonymous referees for the helpful suggestions that improved the final version of this manuscript and especially the reconstruction of the proof of Theorem 3.1.

4 Rotation Group





 Acta Mathematica Scientia(English Series)2020年6期
Acta Mathematica Scientia(English Series)2020年6期
- Acta Mathematica Scientia(English Series)的其它文章
- CONTINUITY PROPERTIES FOR BORN-JORDAN OPERATORS WITH SYMBOLS IN H¨ORMANDER CLASSES AND MODULATION SPACES∗
- ASYMPTOTIC STABILITY OF A BOUNDARY LAYER AND RAREFACTION WAVE FOR THE OUTFLOW PROBLEM OF THE HEAT-CONDUCTIVE IEAL GAS WH SY*
- ON REFINEMENT OF THE COEFFICIENT INEQUALITIES FOR A SUBCLASS OF QUASI-CONVEX MPPG RL L RB*
- EXISTENCE OF SOULUTIONS FOR THE FRACTIONAL (p,q)-LAOLACIAN PROBLEMS INVOLVING A CRITICL SOBLEV EXPNN*
- RADIALLY SYMMETRIC SOLUTIONS FOR QUASILINEAR ELLIPTIC EQUATIONS INVOLVING NONHOMOGENEOUS OPERATORS IN AN ORLICZ-SOBOLEV SPACE SETTING∗
- ON VORTEX ALIGNMENT AND THE BOUNDEDNESS OF TH Lq-NORM OF VIRUICITY IN INCOMPRESSBLE VU FUD*
