一类奇异摄动对流扩散方程组的自适应网格方法的收敛性分析

包小兵，方虹淋，刘利斌

(1.池州学院大数据与人工智能学院，安徽 池州247000; 2.重庆工程学院通识学院，重庆400900; 3.南宁师范大学数学与统计学院，广西 南宁530023)

1.引言

本文考虑如下弱耦合的奇异摄动对流扩散方程组：

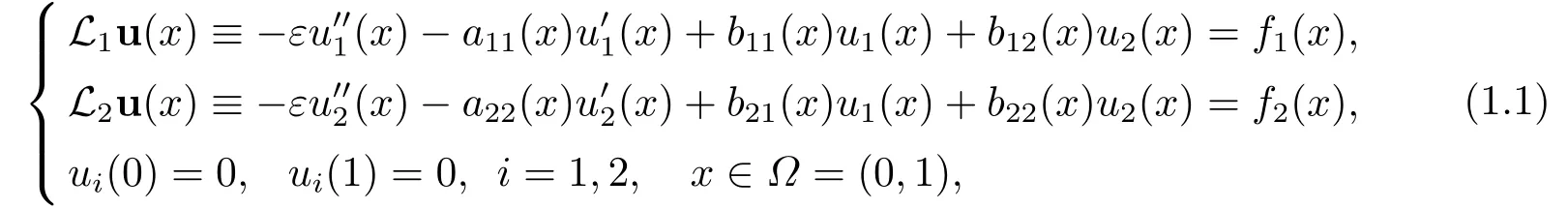
其中0 ＜ε ≪1是摄动参数，u(x)=(u1(x)，u2(x))T，函数aii(x)，bij(x)和fj(x)，i，j =1，2，为足够光滑的函数.假设存在常数α，α*，η，使得

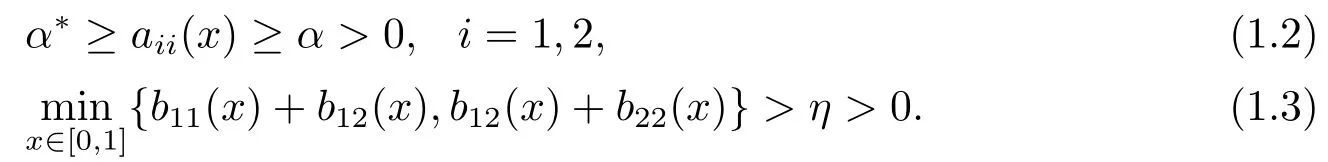
基于假设条件(1.2)-(1.3)，问题(1.1)存在唯一解，且当ε →0时，在x = 0点存在宽度为O(ε|ln ε|)的边界层.[1]

众所周知，奇异摄动问题来源于工程和应用数学的许多分支，例如流体力学、热传导、半导体和化学反应等.[2]一般而言，这类问题所对应的微分方程的高阶导数项包含小的摄动参数，从而导致很难求出其精确解，尤其是非线性的问题.因此，研究这类问题的有效的数值方法显得非常重要.

一直以来，单个奇异摄动对流扩散方程的数值方法备受许多学者的关注.[3]近年来，奇异摄动对流扩散方程组的层适应网格方法逐渐引起了学者们的兴趣.CEN在文[1]中考虑了问题(1.1)的Shishkin网格方法，并证明了数值方法是几乎一阶一致收敛的.Roos和Reibiger[4]考虑了具有单个摄动参数ε 的奇异摄动对流扩散方程组，证明线性有限元方法在Shishkin网格上是几乎二阶收敛的.作者在文[5]中讨论了奇异摄动对流扩散方程组(1.1)的有限差分格式，并在Shishkin网格上证明了数值方法是几乎一阶收敛的.针对奇异摄动对流扩散方程组，LINß[6]在任意网格上构造了一个迎风有限差分格式，并分别在Shishkin网格和Bakhvalov网格上证明了数值方法的收敛阶是O(N-1ln N)和O(N-1) ，其中N表示网格区间的个数.O’Riordan和Stynes[7]讨论了一类强耦合的奇异摄动对流扩散方程组有限差分方法，并在Shishkin网格上给出了数值方法的收敛性.Kumar等[8]讨论了一类奇异摄动对流扩散方程组的Shishkin网格方法，并给出了相应的收敛性分析.

在奇异摄动问题的层适应网格方法受到广泛关注的同时，奇异摄动对流扩散方程的自适应网格算法越来越受到许多学者的青睐[9-14].而关于奇异摄动对流扩散方程组的自适应网格算法，可参见德国学者Linß在2009年发表的文[15].接着，LIU和CHEN在文[16-17]中分别讨论了一类弱耦合和强耦合的奇异摄动对流扩散方程组的自适应网格算法，利用多项式插值技术，给出了离散格式的最大范数的后验误差估计，并以此构造了一个类似于弧长的网格控制函数及相应的网格生成算法.MAO和LIU[18]针对一般的强耦合的奇异摄动对流扩散方程组，构造了迎风有限差分格式的后验误差估计和相应的网格生成算法.值得一提的是文[15-18]所提出的奇异摄动对流扩散方程组的自适应网格算法都是基于后验误差估计和网格等分布原理.如文[10]所述，这种算法属于全离散的自适应网格算法.在文[10，13，19-20]中，基于精确的弧长控制函数和网格等分布原理，作者研究了单个奇异摄动对流扩散方程的半离散的自适应网格算法，并给出了算法的先验误差估计和收敛性分析.因此，本文将在此基础上，系统分析奇异摄动对流扩散方程组(1.1)的自适应网格算法的收敛性.首先，基于标准的迎风差分格式，给出相应的局部截断误差.然后，利用包含方程精确解的网格控制函数、网格等分布原理和精确解的稳定性估计，证明了半离散格式的自适应网格算法是一阶收敛的.最后的数值试验进一步验证了本文的理论结果.

注1.1本文中的C表示与摄动参数ε以及网格参数N无关的正常数，且在不同地方取值不同.对于单个函数v(x)，x ∈= [0，1]，定义最大范数对于向量函数v(x)=(v1(x)，v2(x))T，定义‖v(x)‖=max{‖v1(x)‖，‖v2(x)‖}，‖v(xi)‖=max{|v1(xi)|，|v2(xi)|}，i=0，1··· ，N.另外，为了方便，对于任意函数g(x)，记gi=g(xi).

2.预备知识

在这部分，为了证明问题(1.1)的数值解的误差估计，我们首先列出极大值原理和问题(1.1)的解的稳定性.

引理2.1(极大值原理)[1]假设v(x) 是一个光滑的函数，如果对于任意的x ∈Ω，满足不等式v(0)≥0，v(1)≥0以及L1v ≥0，L2v ≥0，则有v(x)≥0成立.

基于引理2.1中的极大值原理，可进一步得到问题(1.1)的解满足如下稳定性结果:

引理2.2(稳定性)[1]基于假设条件(1.2)-(1.3)，方程组(1.1)的精确解u(x)存在如下稳定性估计:

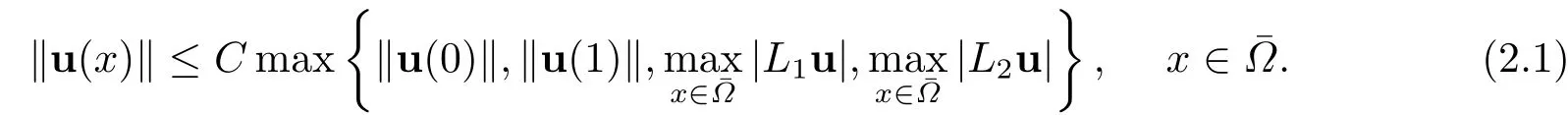
进一步，由文[1]的引理3和引理4，可得如下引理:

引理2.3方程组(1.1)的精确解u(x)的k(k =1，2)阶导数满足如下估计:

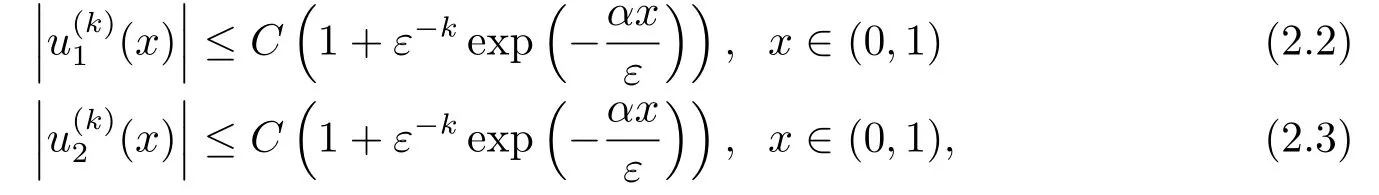
3.离散问题和非均匀网格

为了构造问题(1.1)的离散格式，将区间[0，1]分成N个小区间，即可构造如下的非均匀网格:

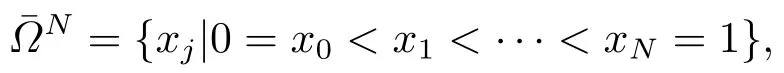
其中网格步长hj=xj-xj-1，则在任意非均匀网格N下，问题(1.1)的迎风有限差分格式为:

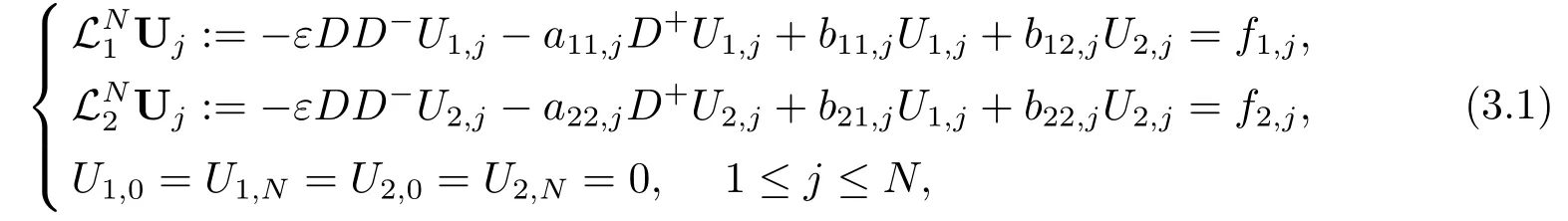
其中Uj=(U1，j，U2，j)T为u(xj)=(u1(xj)，u2(xj))T的近似值，且差分算子定义如下:

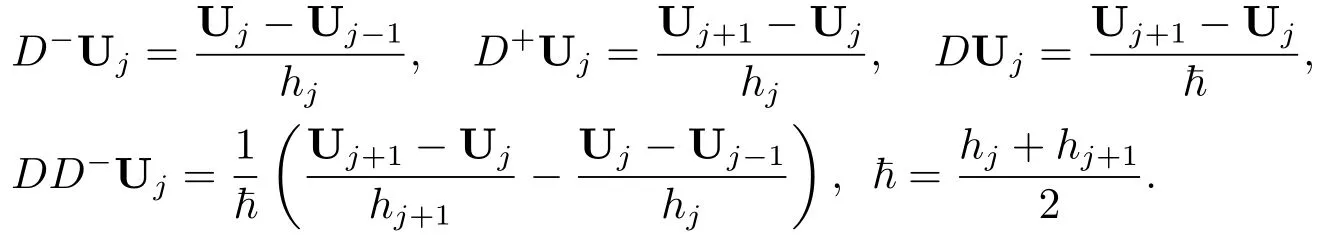
对任意的非均匀网格ΩN，如果存在非负函数M(·，x)，使得

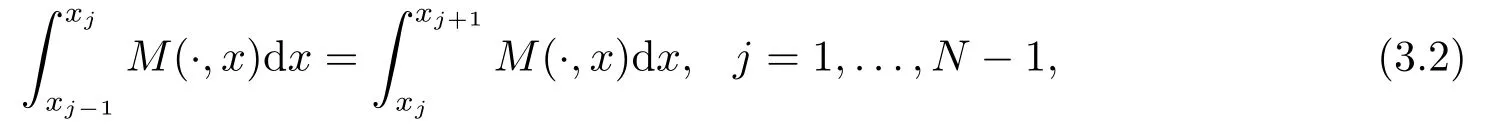
则称此非均匀网格ΩN是等分布的，且M(·，x)称为控制函数.进一步，(3.2)可写为:

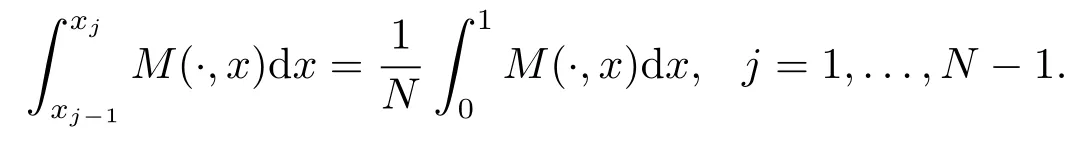
一般情况下，对于单个奇异摄动微分方程，最常用的控制函数为弧长函数M(u(x)，x) =其中u(x)是单奇异摄动问题的精确解.最近，LIU和CHEN[16]以及MAO和LIU[18]构造了奇异摄动对流扩散方程组的自适应网格算法，他们构造了如下的控制函数:

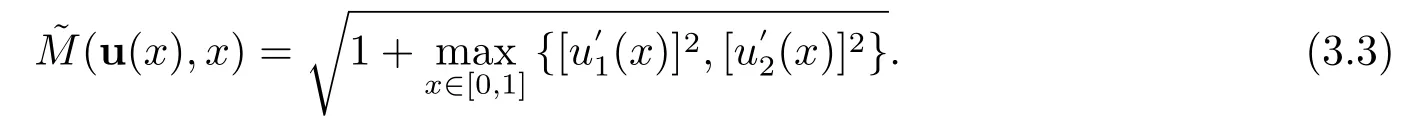
本文也将选取~M(u(x)，x) 作为控制函数来构造自适应网格，即由(3.2)可得，

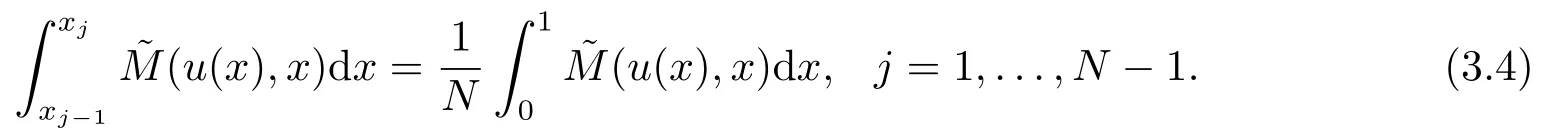
对于任意的ξ ∈(0，1)，构造映射x=x(ξ)∈(0，1)，则有:

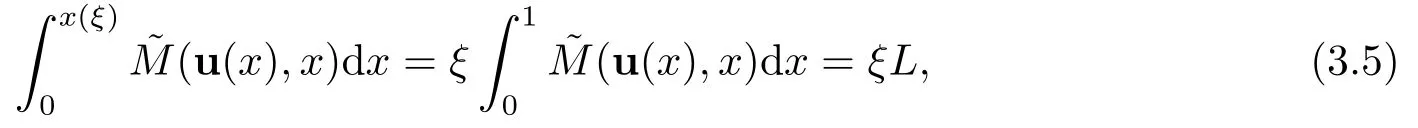
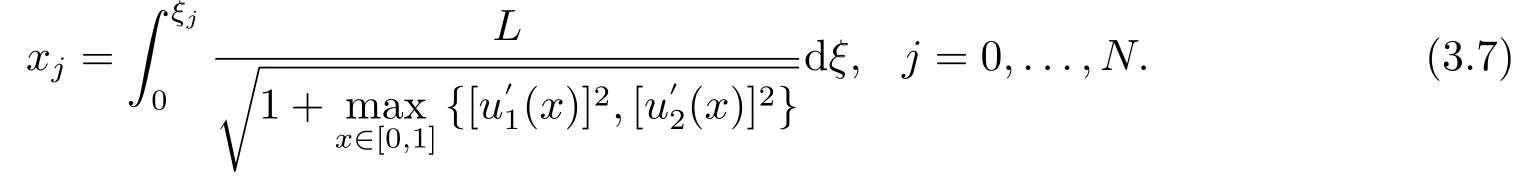
因此，网格步长为:

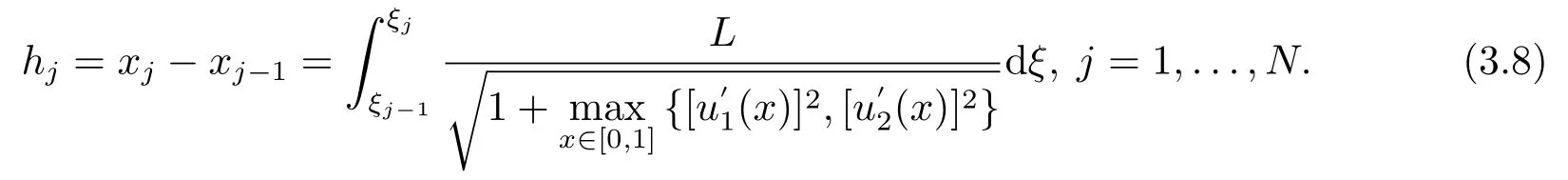
引理3.1对于满足等分布原理(3.4)的任意一个网格有

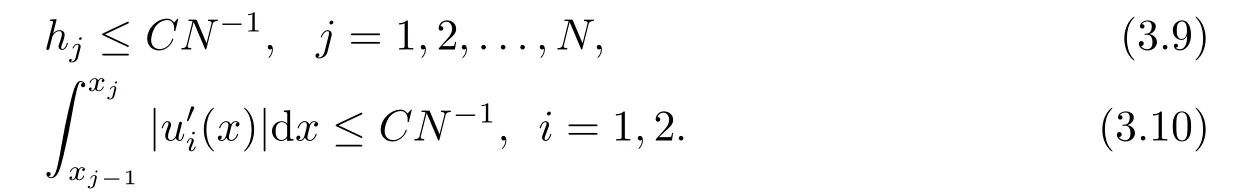
证对于任意的x ∈(0，1)，由引理2.3可以得到弧长

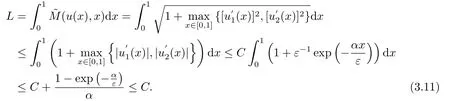
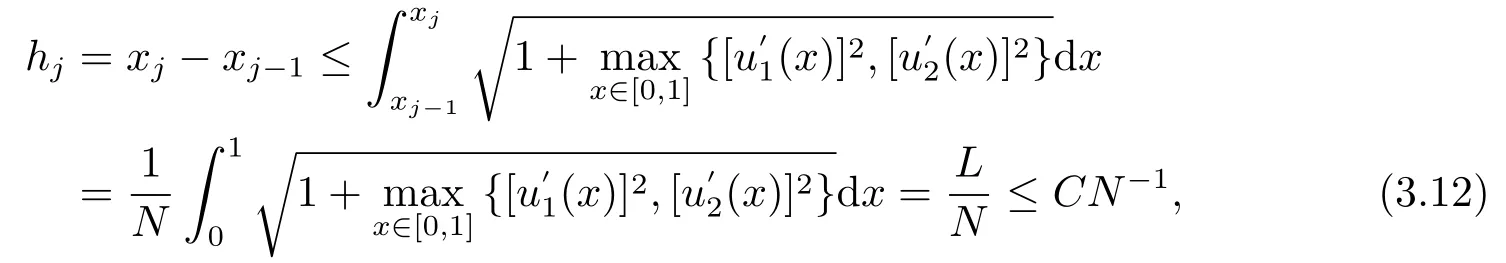
即可得到(3.9)式.

进一步，由(3.6)，(3.11)和(3.12)可得

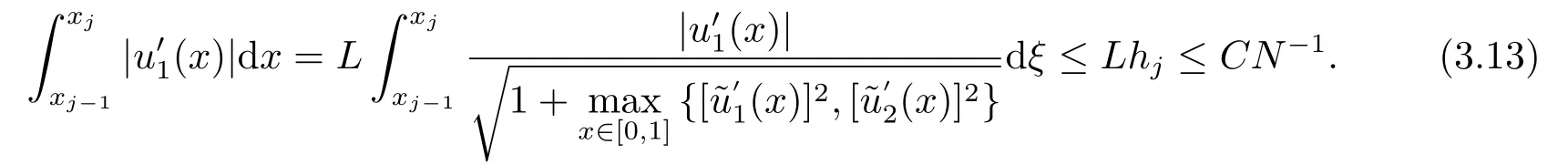
类似地，还可得到:

即完成(3.10)的证明.

4.收敛性分析

显然，离散格式(3.1)在点xj的局部截断误差分别为:

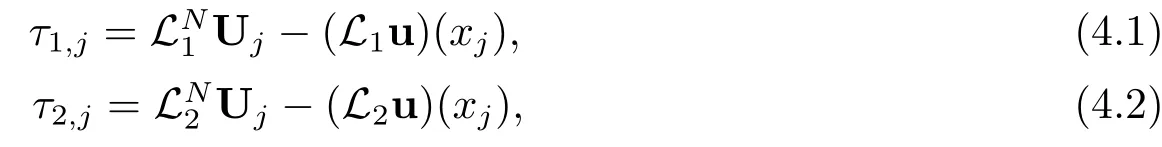
其中u和Uj分别表示方程组(1.1)和离散格式(3.1)的解.

为了给出截断误差的具体表达式，我们首先给出下列引理:

引理4.1[18]对于任意的函数ψ(x)∈ϱ3(，有:

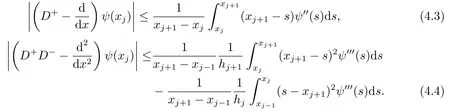
引理4.2设差分格式(3.1)在点xi的局部截断误差为τi，j，则有:

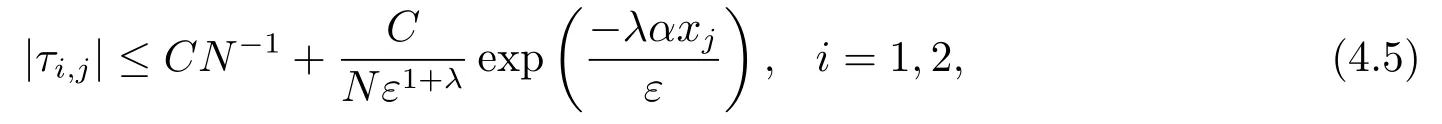
其中C为与参数ε无关的正常数，0 ＜λ ＜1.

证首先，当i=1时，由泰勒展开可得

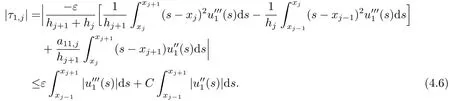
对(1.1)的第一个方程求导，并由(4.6)式和引理3.1可得

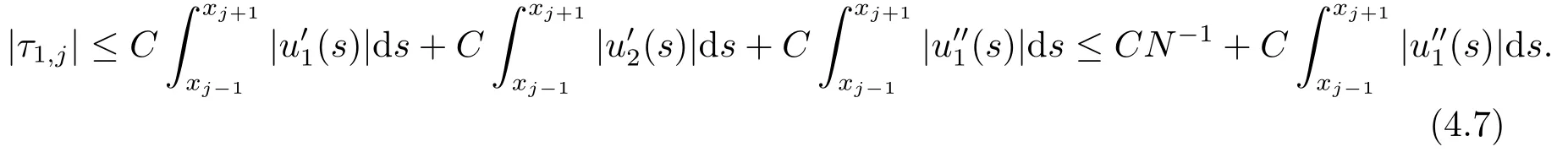
进一步，由(3.7)和(3.11)，可得

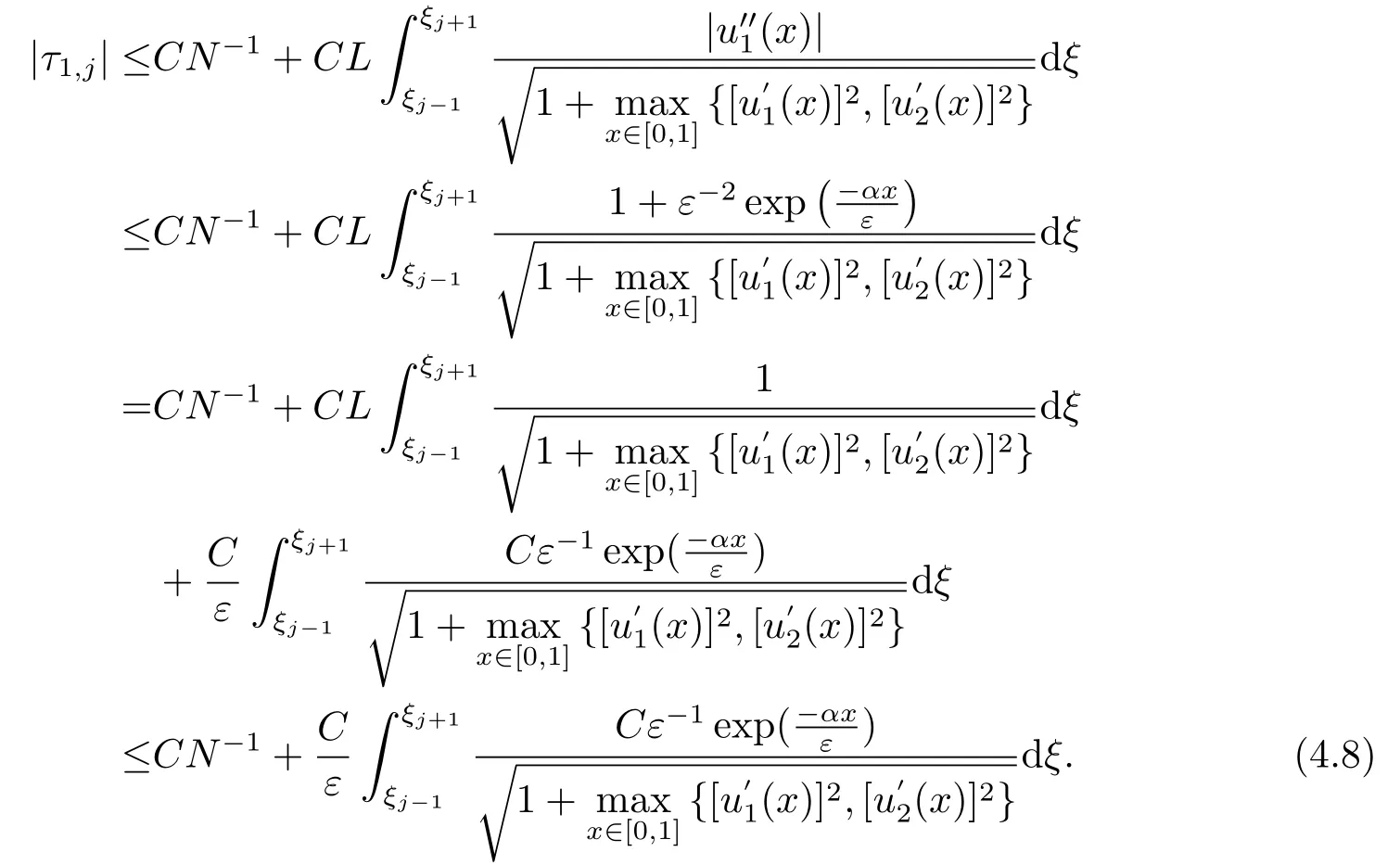
再由引理2.3可得

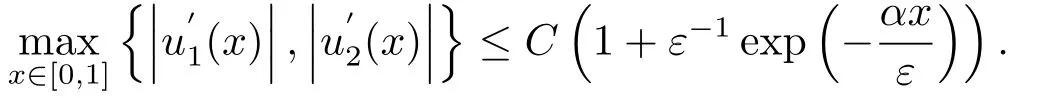
则显然有，

与文[10]的引理5.1类似，存在常数C1和C2，使得:

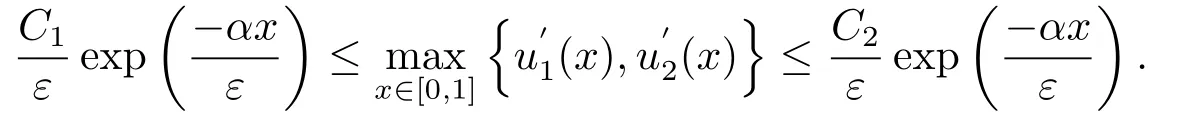
进一步由(4.8)可得

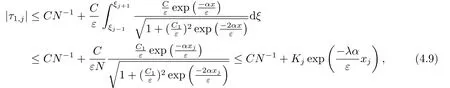
其中0 ＜λ ＜1是与ε，N无关的，并且

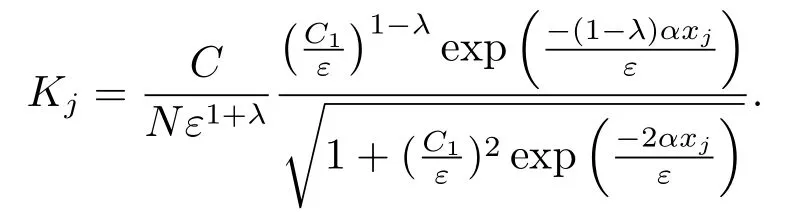
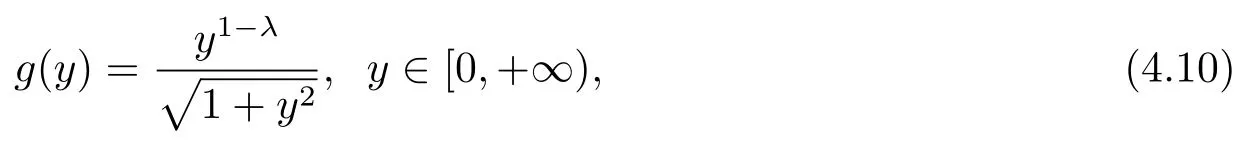
显然，g(y)是区间[0，y*]上的增函数，其中由0 ＜λ ＜1，易知g(y*)≤C，进一步有

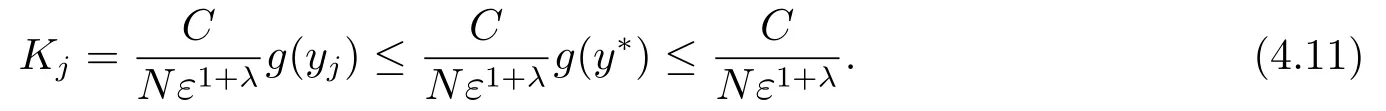
类似地，当i=2时，可以得到:

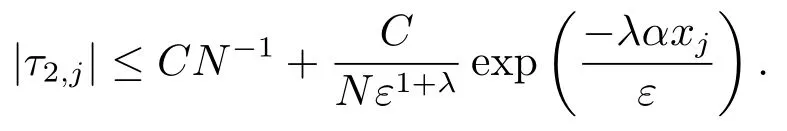
下面为了讨论数值解的误差估计，首先给出网格函数的性质.

引理4.3定义网格函数Sj=(S1，j，S2，j)T满足

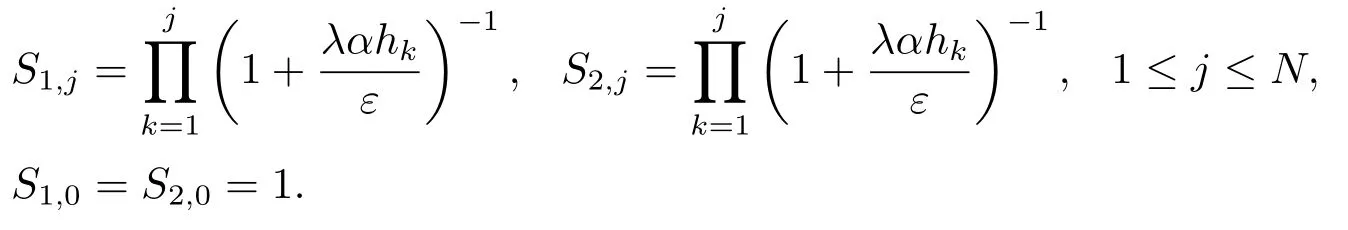
则对于j =1，2，...，N -1，存在一个常数C，使得

证该引理的证明类似于文[19]引理4.4的证明.当i=1时，定义

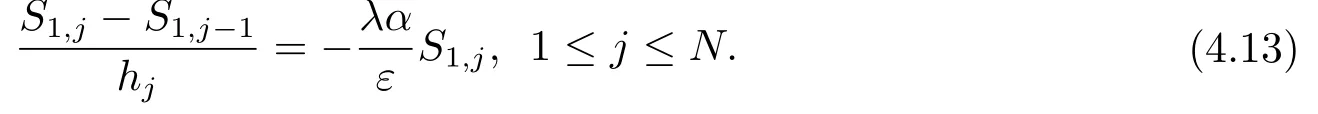
结合式(3.1)和(4.13)可得到

由于hj+1/ħj≤2，则有

当i=2时，同理可证得

下面的引理给出了网格函数Sj的上下界.

引理4.4[19]网格函数满足

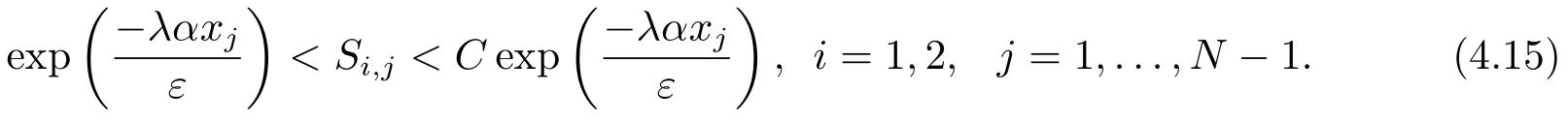
定理4.1令u(x)是方程(1.1)的解，Uj(x)是离散格式(3.1)的解，则

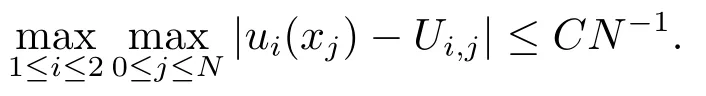
证令ej=(e1，j，e2，j)T=|u(xj)-Uj|为数值解Uj在x=xj(j =0，1，··· ，N)点的绝对误差，则由截断误差τi，j与ei，j的关系可得

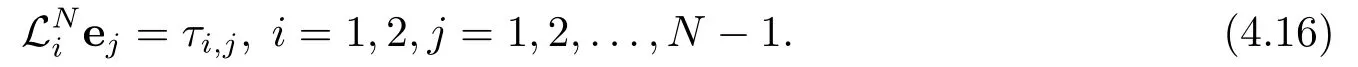
进一步，由引理4.2-4.4，有

由于e0=eN=0，再由引理3.1和比较原理(见文[10]的引理5.3)可得

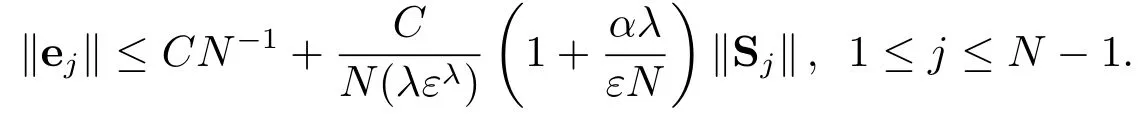
由引理4.3中Sj的定义，有

设摄动参数取值为ε=10-a，其中a是一个正数，选择λ=1/m0，这里m0=max{4，a}，则

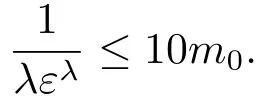
故可以得到‖ej‖≤CN-1，即可完成该定理的证明.

5.数值实验与结果分析

考虑到(3.3)中的网格控制函数包含方程(1.1)的精确解，在实际计算过程中，我们常常构造近似的网格控制函数来代替(3.3).在这一小节，为了验证本文关于自适应网格算法的理论结果，我们将采用文[16，17]中的网格迭代算法来生成相应的自适应网格(在这里，网格终止条件C0=1.3)，并考虑如下奇异摄动对流扩散方程组

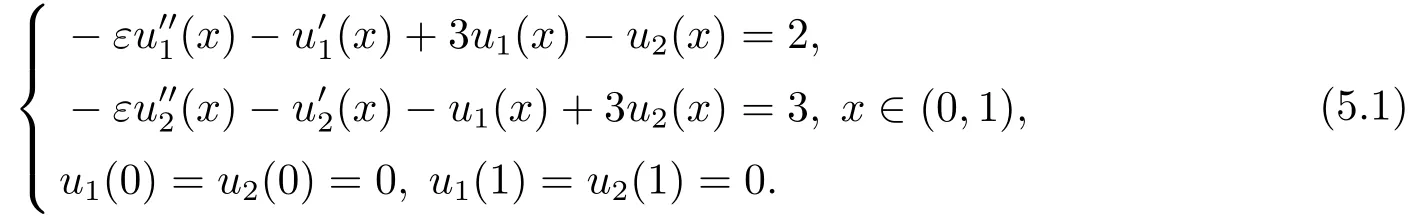
由于该问题的精确解没有给出，我们采用如下公式来计算数值解的绝对误差

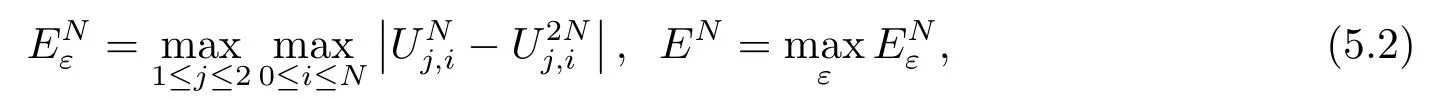
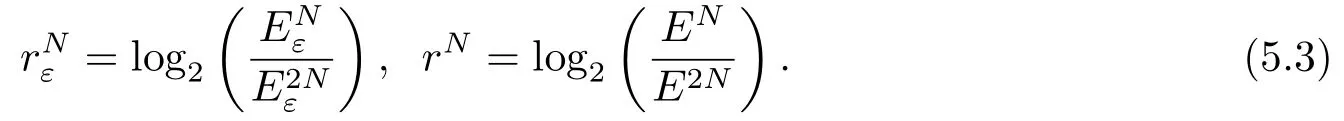
当ε=10-2k，k =0，1，··· ，5，N =2j，j =6，7，··· ，12时，表1中列出了自适应网格算法计算得到的数值结果，其中每一个ε所对应的第三行表示网格生成算法的迭代次数.显然，对于每一个ε，随着N的逐渐增大，本文自适应网格算法的收敛阶逐步达到一阶.对于足够小的ε，网格生成算法的迭代次数也不大，且不随N的增大而增加.当ε=10-5，N =2j，j =6，7，··· ，12时，表2分别列出了迎风有限差分格式(3.1)在均匀网格、Shishkin网格和自适应网格上的误差和收敛阶，其中Shishkin网格的构造见文[1].从表2的数值结果可以看出，本文的自适应网格方法的收敛阶明显比均匀网格和Shishkin网格的收敛阶要高一些，进一步验证了理论结果.

另外，为了进一步的让读者了解自适应网格生成算法的迭代过程，当ε=10-7，N =64时，从下往上看，图1画出了每迭代一次，网格的移动过程.同时，图2给出了问题(5.1)的数值解的变化曲线图.显然，由图1-2可以看出，问题(5.1)的解在x=0点存在边界层.

表1 本文自适应网格方法计算得到的数值结果

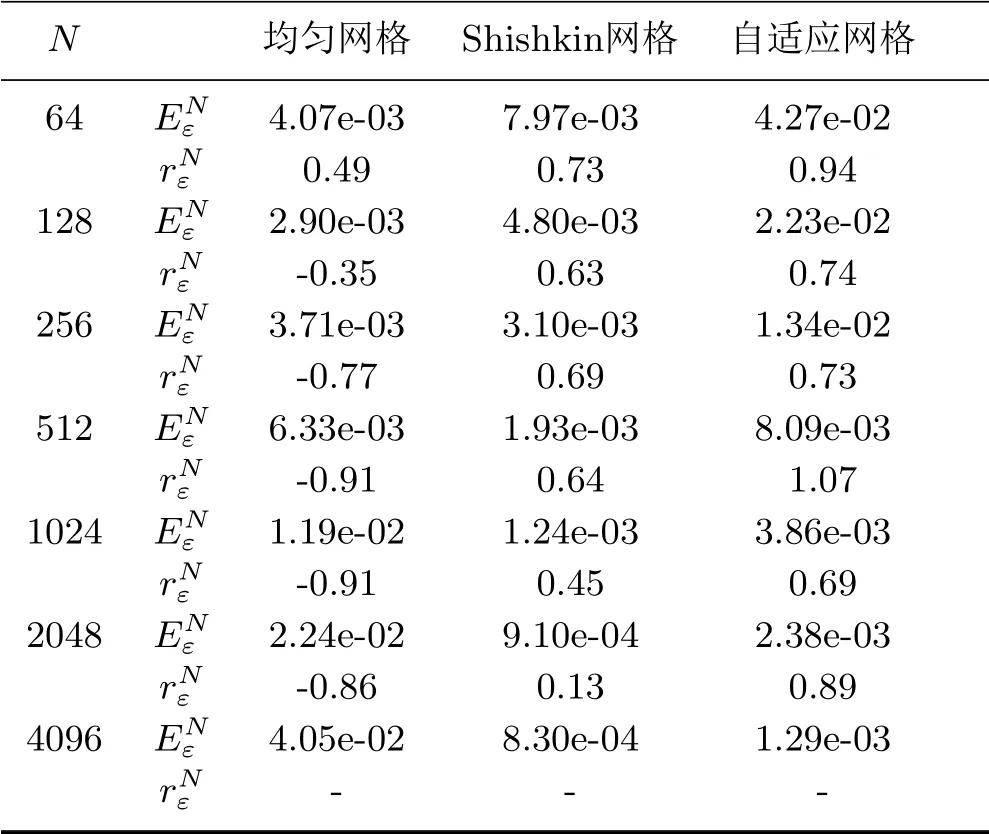
表2 不同网格下的数值结果比较(ε=10－5)

图1 网格迭代过程(ε=10－7，N =64)

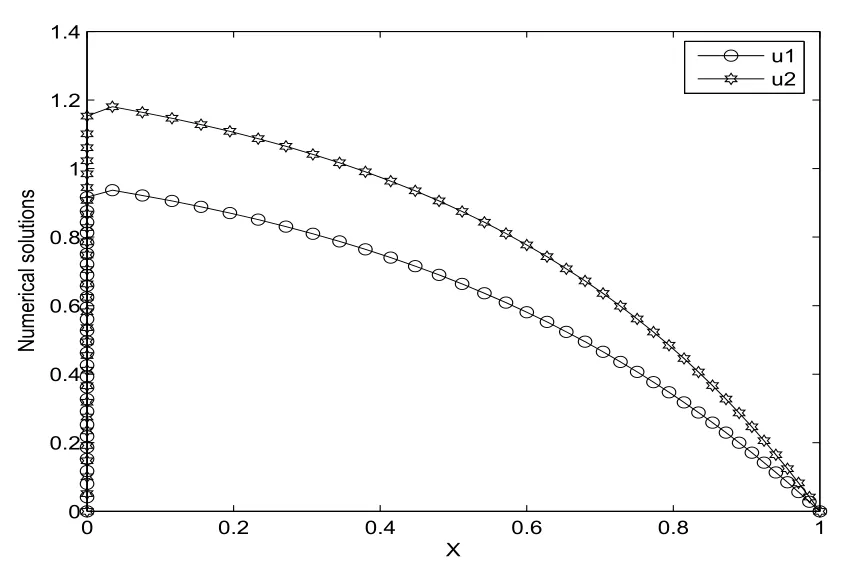
图2 数值解的曲线图(ε=10－7，N =64)

6.结论

本文主要从先验误差估计的角度，分析了一类奇异摄动对流扩散方程组的自适应网格算法的收敛性.首先，利用迎风有限差分格式，在任意的非均匀网格上对方程组进行了离散，并给出了相应的局部截断误差.然后，使用精确解的稳定性估计、网格等分布原理和极大值原理等技术，证明了本文提出的自适应网格算法是一阶一致收敛的.值得一提的是本文的分析方法可以进一步推广到其他奇异摄动微分方程组的自适应网格算法的收敛性分析.