一类分数阶Kirchhoff型方程Schwarz对称基态解的存在性

韩娅玲，向建林

(1.中南财经政法大学统计与数学学院，湖北 武汉430073;2.武汉理工大学数学系，湖北 武汉430070)

1.引言

本文主要研究如下分数阶Kirchhoff型方程

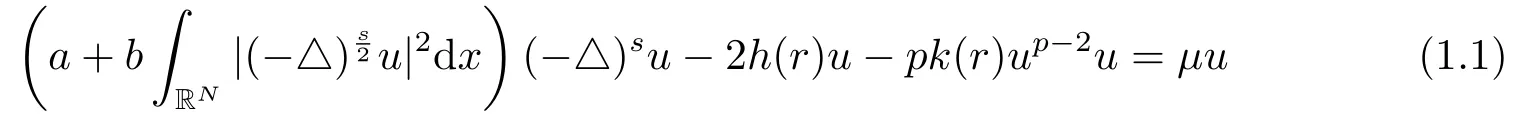
基态解的存在性，其中常数a，b ＞0，s ∈(0，1)，µ是拉格朗日常数，r = |x|，函数h(r)，k(r)满足:

(c1) h:(0，∞)→[0，∞)和k :(0，∞)→[0，∞)Lebesgue可测且有界;

(c2) h和k关于r单调非增.

近年来方程(1.1)受到广泛关注，特别当s=1时，方程(1.1)表示弦振动中经典的Kirchhoff方程，此时方程(1.1)解的存在性及其相关性质可见文[1-2]，多重性结果见文[3]，峰解见文[4]，唯一性见文[5]，爆破分析见文[6]等.当0 ＜s ＜1时，文[7]研究了方程(1.1)含临界指数情形基态解的存在性，文[8]探讨了方程(1.1)解的多重性.而关于方程(1.1)Schwarz对称基态解的存在性，据我们所知，暂时未见结果.

若b = 0，则方程(1.1)就是通常意义下的分数阶Laplacian方程.近二十年来，分数阶Laplace算子由于在数学物理和相关领域的广泛应用，受到非常多数学研究者的关注，特别是Nezza等在文[9]中得到分数阶Sobolev嵌入不等式后，许多数学研究者在分数阶Laplacian方程解的存在性，唯一性和非退化性等方面得到了非常丰富的结果[10-15].值得一提的是，利用约束变分理论和常微分方程理论，文[11-12]分别得到了一维和高维情形分数阶Laplacian方程基态解的存在性和唯一性.文[13]利用约束变分思想和集中紧引理得到了一般的非线性情形分数阶Laplacian方程基态解的存在性.进一步文[14]证明了一般非线性条件下分数阶Laplacian方程对称基态解的存在性，并利用非线性和方程(1.1)非线性相同且满足条件(c1)和(c2)的情形证明了一般非线性情形时部分条件的最佳性.本文的目的是希望能将文[5，14]的结果推广到含分数阶的Kirchhoff方程(1.1)中来，进而探讨方程(1.1)对称基态解的存在性.但是由于非局部项的存在，文[14]中的条件(F5)不能满足，需要提出新的想法.同时由于非局部项的存在，相应基态解存在的非线性项指数范围更加复杂，需要更细致的估计.

方程(1.1)对应的能量泛函为

由临界点理论可知方程(1.1)的解就是相应能量泛函I(u)的临界点.而方程所有解中能量最小的解称之为方程(1.1)的基态解，如果解还具有Schwarz对称性，则称为Schwarz对称基态解.因此讨论方程(1.1)Schwarz对称基态解的存在性可以转化为研究如下极小化问题的Schwarz对称极小解的存在性:

其中

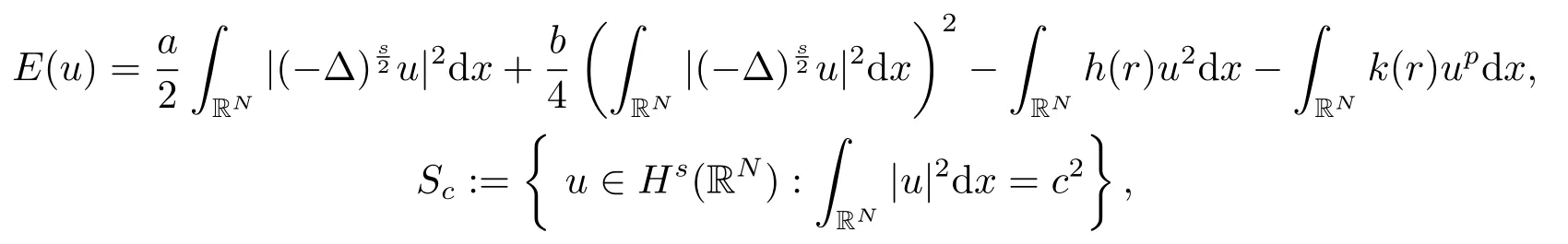
c是常数，0 ＜s ＜1.Hs(RN)是通常的Besov空间

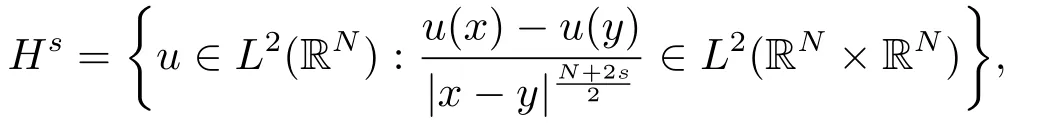
相应范数为:

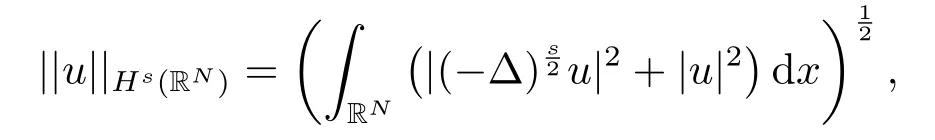
其中

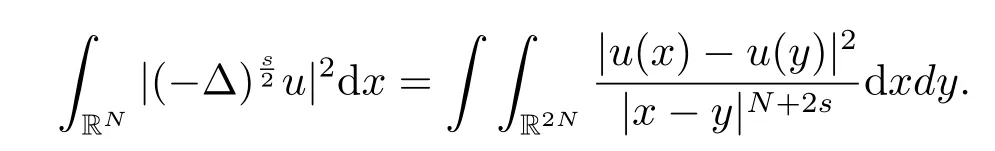
可得到本文的主要结论为:

定理1.1假设函数h(r)，k(r)满足条件(c1)和(c2).则

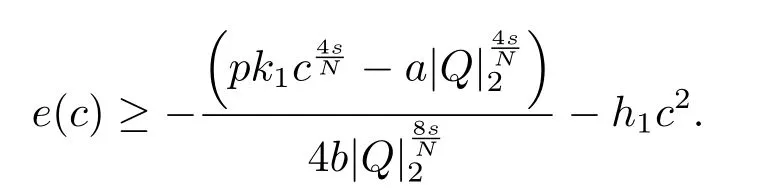
若c ≤c1且h(r)是常值函数，则极小化问题(1.2)不存在非零极小解.

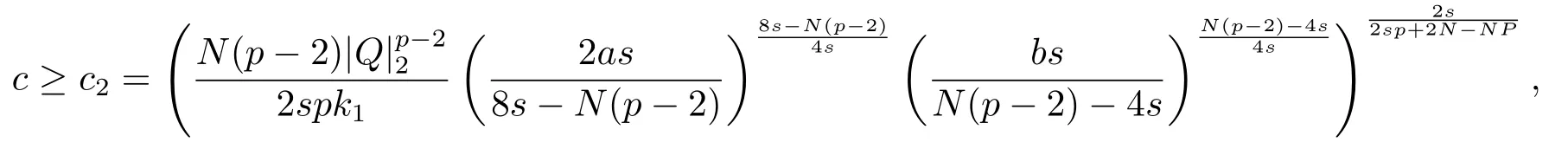
极小化问题(1.2)存在Schwarz对称极小解，且此时

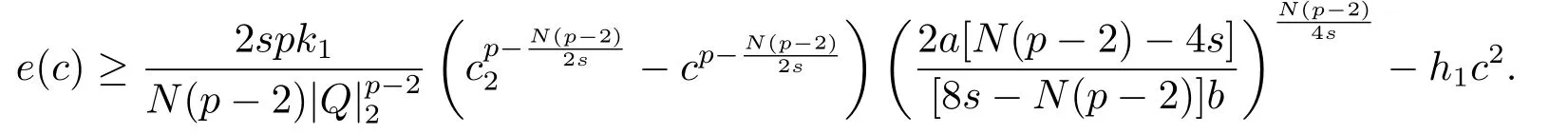
若c ＜c2且h(r)是常值函数，则极小化问题(1.2)不存在非零极小解.

注假设u ∈Sc使得e(c) = E(u)，由定理可知如果问题(1.2)存在极小解，则能量e(c) ＜0，进一步可知存在一个Lagrange乘子µ，使得方程(1.1)成立，即容易知道极小化问题(1.2)的Schwarz对称极小解就是方程(1.1)的Schwarz对称基态解，且

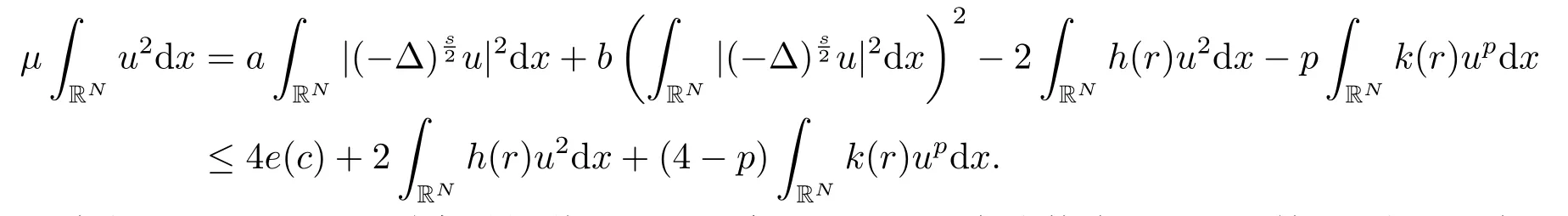
因此当h(r) = 0，p ≥4时容易知道Lagrange乘子µ ＜0.而在分数阶Laplacian情形，由于没有非局部项，会简单一些.

2.准备工作

在证明本文定理前，先介绍如下分数阶Gagliardo-Nirenberg不等式[12]

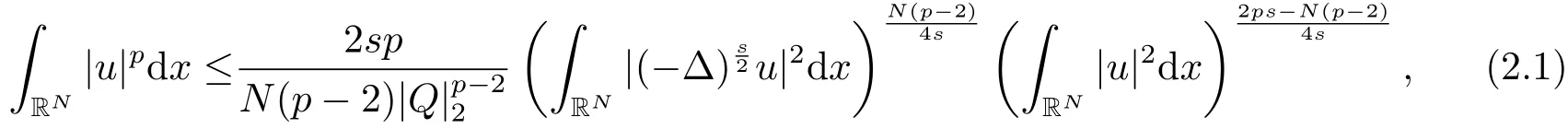
上述等式成立当且仅当u(x)是函数Q(x)的伸缩平移，其中Q(x)是下述非线性分数阶方程唯一径向对称正解:

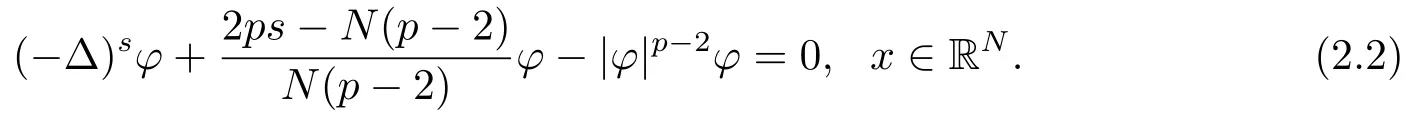
由方程(2.2)和Pohozaev恒等式有

引理2.1对任意的θ ＞1，有e(θc)≤θ2e(c).

证对任意θ ＞1，设uθ(x)=u(θ

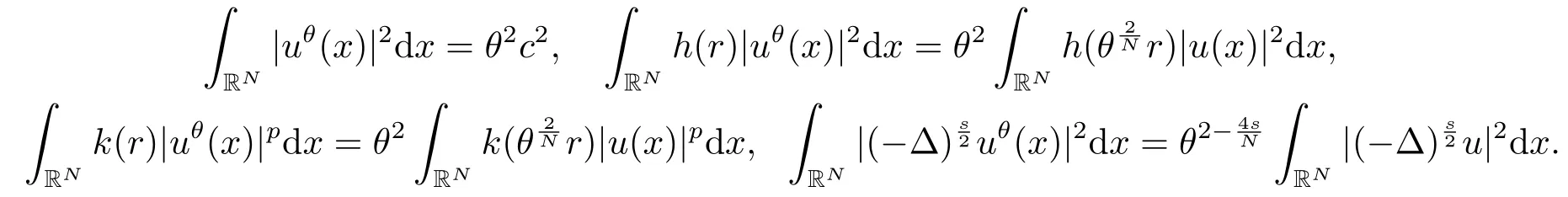
因此，由条件(c2)可得

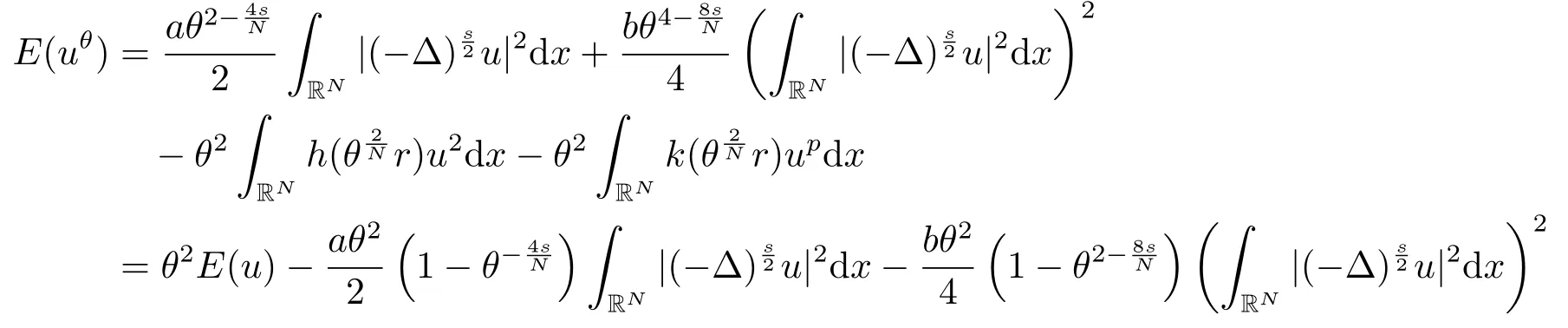
这意味着对任意的θ ＞1，有

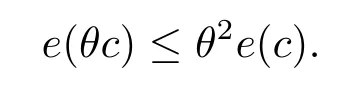
引理2.2假设{un}是一列Schwarz对称的极小化序列，如果在Hs(RN)上un⇀u，则E(u)≤lim infn→∞E(un).

证由文[9]可知，范数||u||Hs具有弱下半连续性

进一步可得

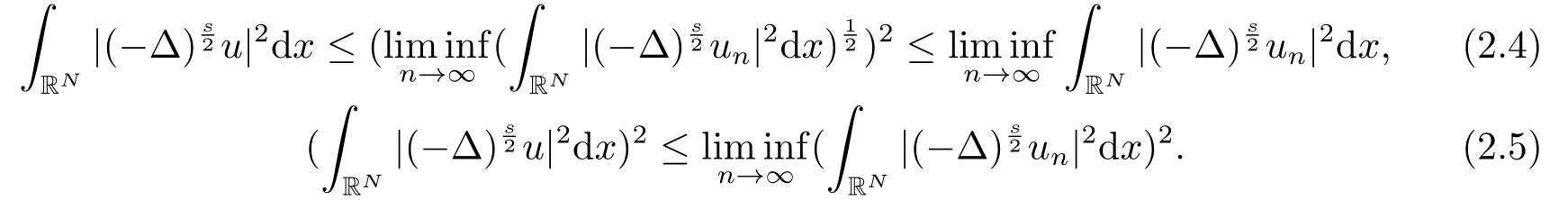
设R ＞0是一个常数，记BR(0)={x ∈RN:|x|≤R}，则

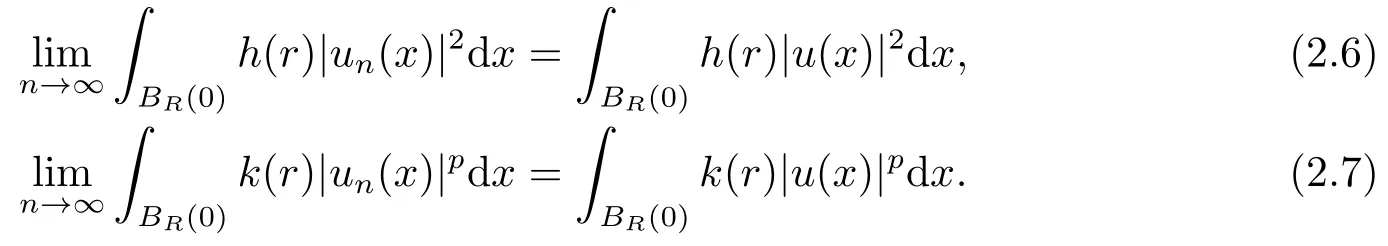
一方面，由函数h(r)，k(r)的有界性，存在h1，k1，使得

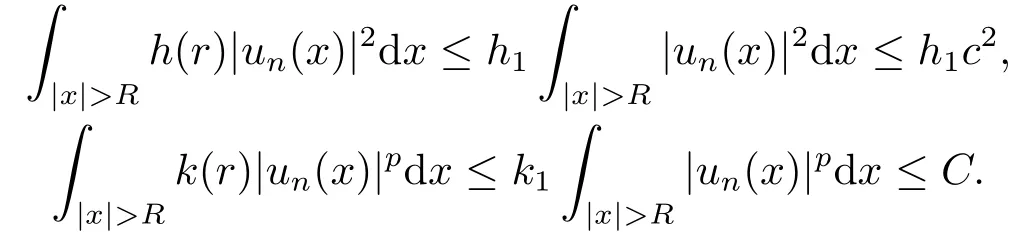
另一方面，由条件(c2)，不妨设limr→∞h(r) = h(∞) = 0 = k(∞) = limr→∞k(r)，综合上述各式，可得

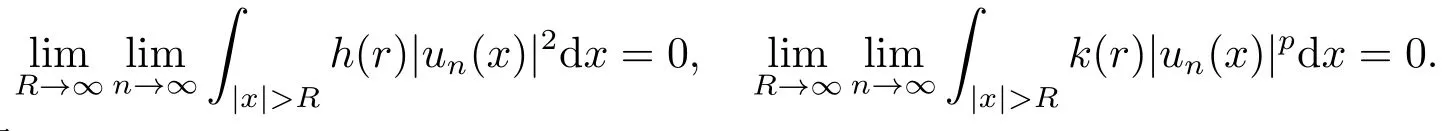
同理可得

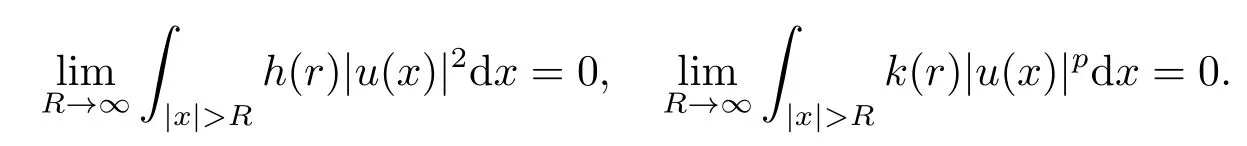
上述两式结合(2.6)和(2.7)可得

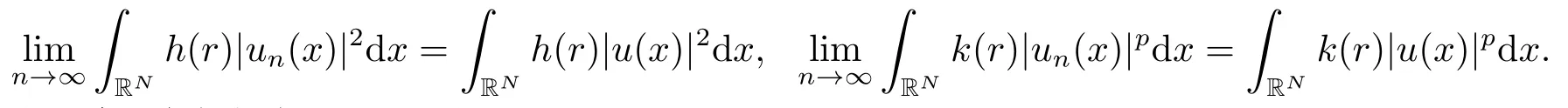
进一步，结合上式和(2.5)可知

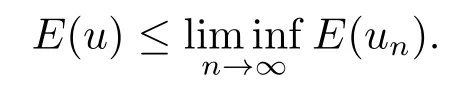
引理2.3假设函数其中t ＞0，则

证由函数gp(t)的定义易知gp(0)=-h1c2.

当c ＞c1时，通过计算(t)=0可得函数gp(t)在(0，+∞)上有唯一极小值点为

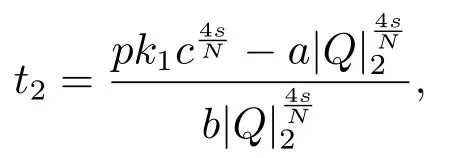
进一步可得函数gp(t)在(0，+∞)上取得极小值

进一步可知当t →∞时gp(t)→-∞，因此gp(t) 无法达到极小值.

引理2.4假设函数h(r)，k(r)满足条件(c1)和(c2)，则

证对任意的u ∈Sc，利用Gagliardo-Nirenberg不等式，可得

对任意的u ∈Sc，做伸缩可得

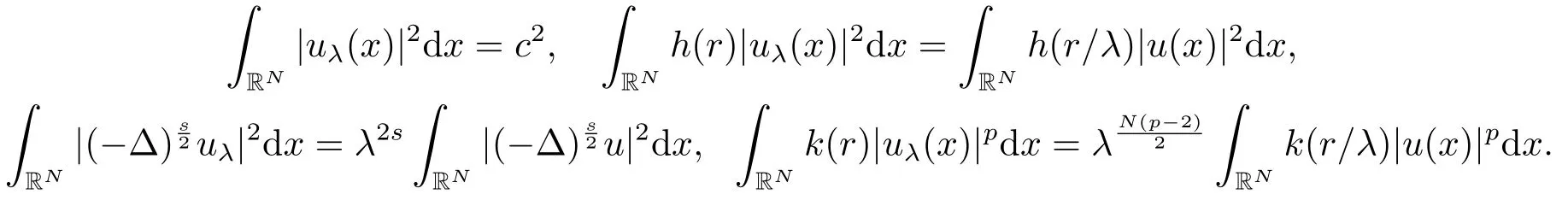
因此有

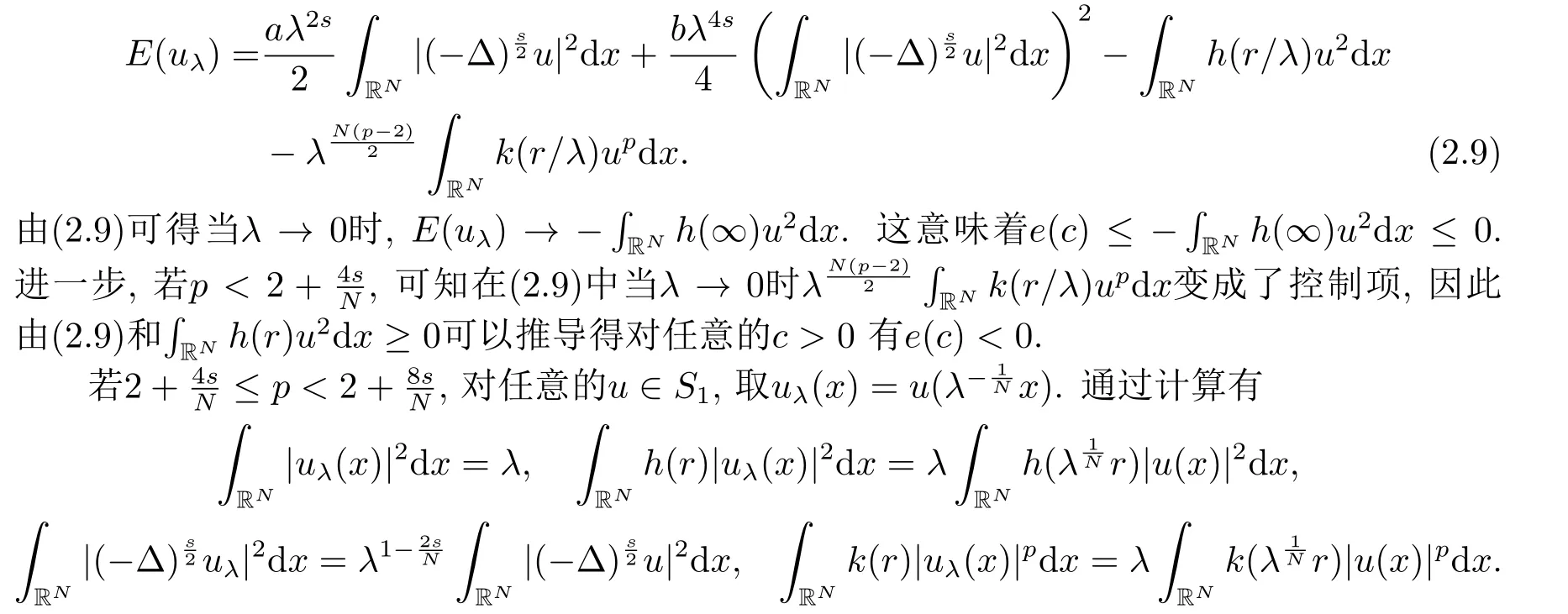
由上述等式，可得

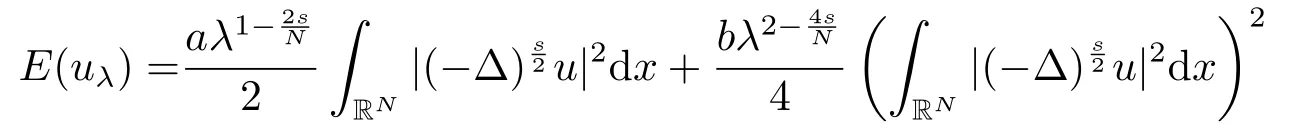
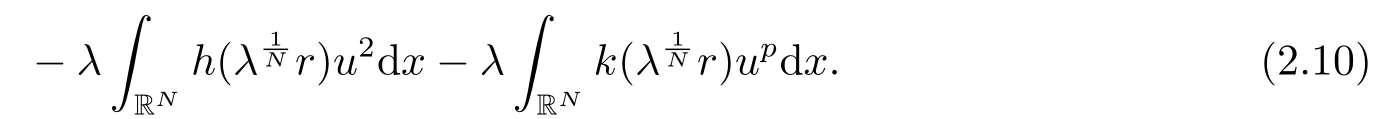
3.定理证明

定理1.1的证明1) 当2 ＜p ＜2+时: 由引理2.3中(i)知，对∀c ＞0，gp(t) ≥gp(t1)，因此e(c) ≥gp(t) ≥gp(t1)，即e(c) ＞-∞.对任意的u ∈Hs(RN)，易知|u| ∈Hs(RN)且E(|u|) =E(u).由文[16] 中定理A.1可知当0 ＜s ＜1时关于dx的严格重排不等式成立.设{un}是极小化问题(1.2)的一个极小化序列，表示un的对称递减重排，则满足

(i) 对任意x ∈RN，≥0;

(iii) 对任意的r ∈[1，∞)，若un∈Lr，则||r=|un|r;

(iv) 若un∈Hs(RN)，则

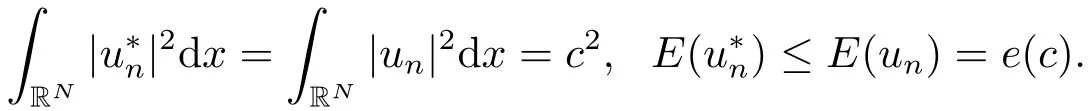
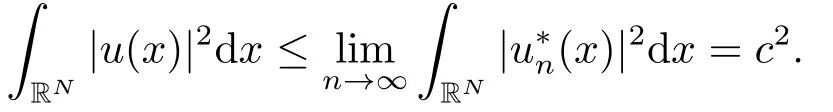
利用引理2.2可得

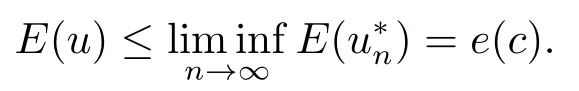
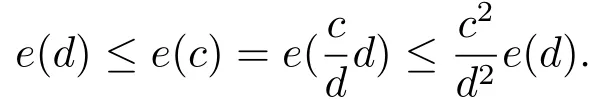
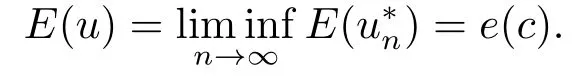
因此极小化问题(1.2)存在正的极小解u.设u*是正极小解u的对称递减重排，相似文[17]中定理1可得

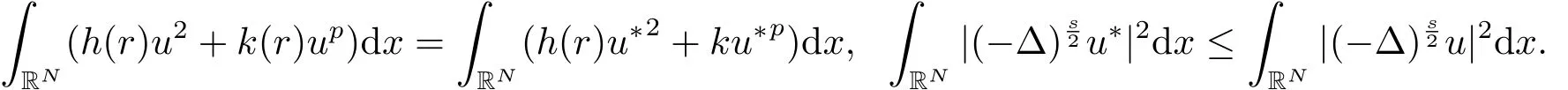
经过简单的计算即得E(u*)≤E(u).因此极小化问题(1.2)的解u是Schwarz对称的.进一步，由引理2.3中(i)可知此时的极小值e(c)≥gp(t1).

若c ≤c1，由引理2.3中(ii)知e(c) ≥gp(t) ≥-h1c2.令其中λ是一个常数，Q(x)是(2.2)的非负径向解，因此即uλ(x) ∈Sc.通过计算，利用(2.3)，可得

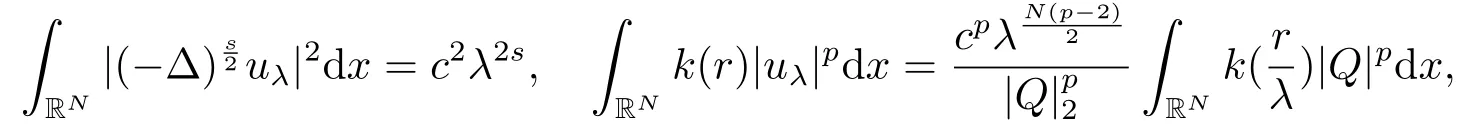
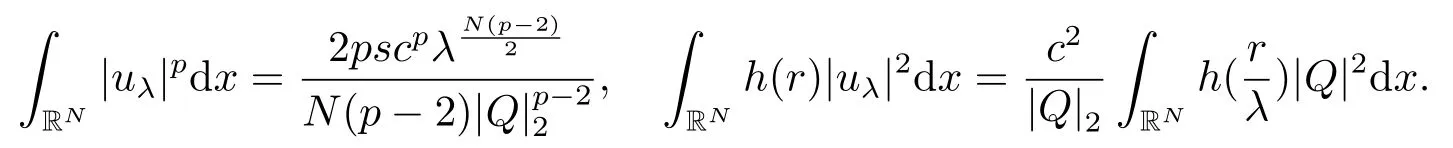
因此当λ →0+时，

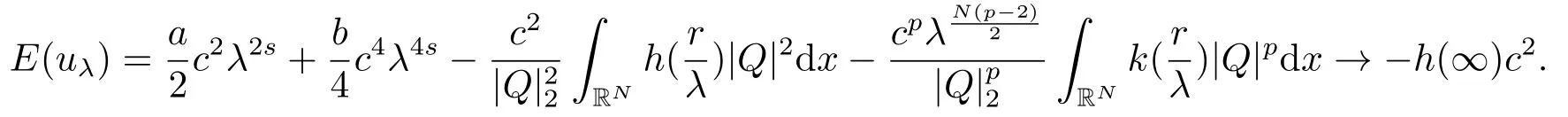
因此只有当h1= h(∞)，即h(r)是常数时才能证明当c ≤c1时极小化问题(1.2)不存在非零极小解.

若c ＜c2，结合引理2.3(iii)，相似上面情形2)c ≤c1时的证明可得当c ＜c2时只有当h1=h(∞)，即h(r)是常数时才能证明极小化问题(1.2)不存在非零极小解.

当c ＞c3时，由引理2.3中(iv)知e(c) ≥-∞; 令其中λ是一个常数，Q(x)是(2.2)的非负径向解，当λ →+∞时可得

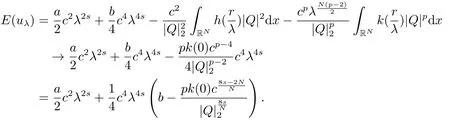
因此当k(0)=k1时，E(uλ)→-∞，即k(r)是常数时对所有的c ＞c3，极小化问题(1.2)不存在极小解.

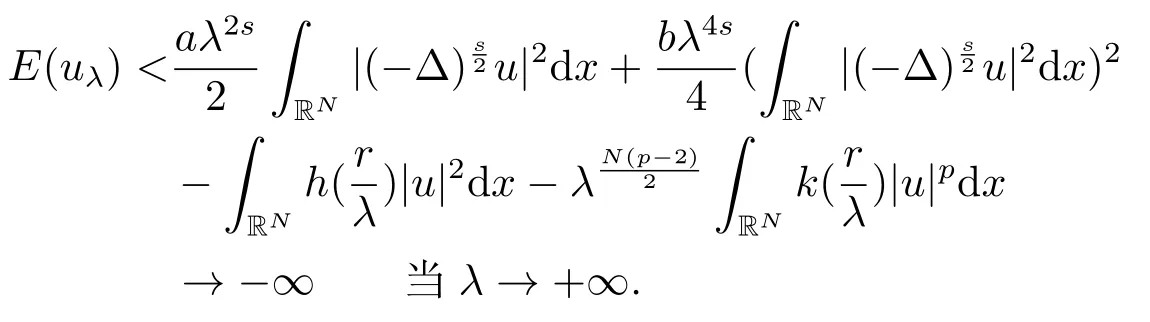
即对所有的c，e(c) = -∞，这意味着当p ＞2+时极小化问题(1.2)不存在Schwarz对称极小解.