证明绝对值不等式的八个推理策略

江苏省金湖县第二中学 (211600) 梁加林

含绝对值的不等式是一个综合性问题，而其与不等式相结合的问题是高考和其他选拔性考试中加大区分度的重要选择内容之一，其求解过程需要综合考虑，在用好绝对值不等式的性质的同时，需要考察具体题目的特点，研究出题者的考试意图和目的，制定合理可行的富有特色的将它方案．本文从如何分析题目、解决具体问题的角度出发，介绍八种常见的推理策略，希望给读者朋友一点启发．

一、分析推理

在一些相对复杂的不等式问题的推理过程中，经常采用“由果索因”的手段，即从结论出发步步逆推，直到找到能使结论成立的理论依据，这样也就完成了题目证明的过程．

例1 已知函数f(x)=|x+1|，若|a|>1,|b|>1，求证：f(ab)>f(a)-f(-b).

证明：因为f(a)-f(-b)=|a+1|-|-b+1|≤|a+1-(-b+1)|=|a+b|，所以要证f(ab)>f(a)-f(-b)，只需证|ab+1|>|a+b|，即证|ab+1|2>|a+b|2，即证a2b2+2ab+1>a2+2ab+b2，即证a2b2-a2-b2+1>0，即证(a2-1)(b2-1)>0.因为|a|>1，|b|>1，所以a2>1，b2>1，所以(a2-1)(b2-1)>0成立，所以原不等式成立.

评注：由于要证的不等式中含有绝对值符合，比较复杂，直接用综合推理不太顺畅，所以采用了分析法.一般的，如果含有分式、根式、绝对值等问题采用分析法效果是明显的．

二、活用公式

利用绝对值不等式|a|-|b|≤|a±b|≤|a|+|b|,进行“放大”或“缩小”是解决与绝对值相关的不等问题最常用的思路．

例2 已知f(x)=ax2+bx+c对于一切实数x∈[-1，1]都有|f(x)|≤1，证明对于一切x∈[-1，1]都有|2ax+b|≤4．

解析：从|f(x)|≤1到|2ax+b|≤4需通过一些特殊的函数值来建立不等关系，如f(0),f(-1),f(1)等，然后用绝对值不等式来证明．依题意可知|f(0)|≤1，|f(-1)|≤1，|f(1)|≤1，即|c|≤1，|a+b+c|≤1，|a-b+c|≤1,则|2a+2c|≤|a+b+c|+|a-b+c|≤2,即|a+c|≤1,所以|2a+b|=|(a+b+c)+(a+c)-2c|≤|a+b+c|+|a+c|+|2c|≤4, 且|2a-b|=|(a-b+c)+(a+c)-2c|≤|a-b+c|+|a+c|+|2c|≤4,又当x∈[-1,1]时, |2ax+b|≤{|2a+b|,|2a-b|}，所以|2ax+b|≤4．

评注：在“放大”或“缩小”的过程中，其关键是合理的配凑，就是将需要证明的结论通过适当的配凑分解成与已知条件相关的不等式．本题中利用两次“放大”后达到了解题目的，要注意在“放大”或“缩小”时必须保持不等号方向一致．

三、及时消参

如若所给的条件式中只含有一个参数，并且也已知这个参数的范围，可直接运用绝对值不等式的性质进行放缩，消去参数，达到解题目的．

评注：在解题中抓住了|a|≤1这个关键条件，通过分离参数再运用绝对值不等式的性质进行放缩处理，消去了参数a，这是为后续的解题扫清了障碍．

四、巧取特值

在已知的函数式中，若含有字母系数，其中取特殊值是一个重要的解题手段，由此可显露出所求不等式中有关部分的内在联系，从而确定可行的解题方案．

例4 已知a,b,c∈R, 若已知函数f(x)=ax2+bx+c,g(x)=ax+b, 当x∈[-1,1]时，有|f(x)|≤1成立．(1)证明：|c|≤1；(2)当x∈[-1,1]时，求证：|g(x)|≤2．

证明：(1)由于x∈[-1,1]时，|f(x)|≤1, 而0∈[-1,1]，则必有|f(0)|=|c|≤1．

(2)由于g(x)=ax+b为单调函数, 其图像是一条直线，要证|g(x)|≤2, 只须证|g(±1)|≤2,由|xg(x)|=|ax2+bx|=|f(x)-c|≤|f(x)|+|c|≤1+1=2, 取x=±1时, 有|g(±1)|≤2，故必有|g(x)|≤2成立．

评注：本题中参数多，含有两个函数式，要完成题目的证明首先充分挖掘了一次函数的有关性质，利用特殊值将待证式进行简化；然后再挖掘两个函数之间的特殊关系，并巧妙地合理配凑，使整个证题过程变得顺畅自如．

五、重新组合

在给定的定义域内，通过取特殊值，建立含参数的等式，然后以消去参数为目的进行有目标的重新组合，再运用绝对值不等式的性质进行放缩处理，达到解题的目的．

评注：本题中的结论与一个常数有关，那么如何消去题目中的参数就是解题目标，利用给出的条件先表示出含参数等式，通过有目的地配凑，再由不等式性质进行整体处理，达到证题目的，这些都是证明含绝对值的不等式常用手段，应该得到理解和重视．

六、引入参数

如果在用拼凑组合消去系数时，遇到了困难，可通过引入新参数，然后再运用待定系数法求出这个参数，建立有关的等式．

例6 设函数f(x)=ax2+bx+c对于一切x∈[-1,1]都有|f(x)|≤1，求证：对于一切x∈[-1,1]都有|3ax+b|≤6．

证明：设g(x)=3ax+b，g(1)=mf(1)+nf(-1)+kf(0)，则3a+b=m(a+b+c)+n(a-b+c)+kc=(m+n)a+(m-n)b+(m+n+k)c，通过比较多项式的系数可知：m+n=3且m-n=1且m+n+k=0；解由此三式联立所得方程组得：m=2；n=1；k=-3；即g(1)=2f(1)+f(-1)-3f(0)．又对于一切x∈[-1,1]都有|f(x)|≤1，则|f(1)|≤1；|f(-1)|≤1；|f(0)|≤1；故而|g(1)|=|2f(1)+f(-1)-3f(0)|≤2|f(1)|+|f(-1)|+3|f(0)|≤2+1+3=6．同理可证|g(-1)|≤6，由一次函数的性质可知|g(x)|≤6，即|3ax+b|≤6．

评注：待定系数法是解决多项式“恒等”问题的有力工具，在本证题中比较恰当地使用了此法，给人有打破常规、耳目一新的感觉，降低了解题的难度．

七、反解系数

如若题目中欲证明与系数相关的不等式，可通过取特殊值将所求系数用关于特殊的函数值表示出来，然后再运用不等式进行放缩推理．

例7 若f(x)=ax2+bx+c(a,b∈R)在区间[0,1]上恒有|f(x)|≤1，求证：|a|+|b|+|c|可能的最大值为17．

八、抓住性质

对于二次函数问题，二次函数的图像和性质是解决问题的有力武器，及时地加以运用，可简化解题过程，提高解题效率.

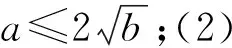
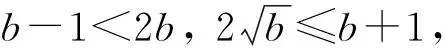
评注：在解决本题第(1) (2)问时，及时的运用了二次函数的图象及性质，再结合已知的绝对值不等式的条件，运用绝对值的意义进行转化，这样就建立了相关的不等式组，这就是抓住了解题的关键所在，将难点轻松化解了．