“圆”来如此
蔡雄壮


【摘要】构造辅助圆,建立圆的模型,运用圆的相关知识解决几何问题,化难为易,化隐为显,会带来柳暗花明的效果.文章归纳构造辅助圆解几何题的五种类型以及依据,并列举案例分析阐述如何运用相应的类型来构造辅助圆解几何题,从根源上解决学生的困惑,让学生知其所以然.
【关键词】辅助圆;几何题;模型;类型
在解几何题时,经常通过作辅助线,化繁为简、化难为易,让题目迎刃而解.对于有些几何题,相比其他解法,构造辅助圆,建立圆的模型,运用圆的相关知识解决问题,会带来意想不到的效果,惊叹构造辅助圆的妙处.
一、由一道模拟题引发的思考
课堂上讲解一份泉州中考数学模拟卷时,其中一道选择题,有学生提出不同的解法,并且这种解法简单、明了,学生容易理解,但如何准确构造出辅助圆是解决问题的关键,这引发了笔者的思考.笔者对如何构造出合适的辅助圆进行了深入的探究.
(一)原题呈现
图1如图1,在菱形ABCD中,点P是BC边上的一动点,连接AP,AP的垂直平分线交BD于点G,交AP于点E,在P点由B点向C点(不与C点重合)运动的过程中,∠APG的大小变化情况
是( ).
A.变大 B.先变大后变小
C.先变小后变大 D.不变
(二)解法探究
解法一:根据“线段垂直平分线的性质定理”和“角平分线的性质定理”作辅助线.
分析:由“见垂直平分线,连端点,得等线段”,连接GA.由EG垂直平分AP,知GA=GP.由“见角平分线,作双垂线,得等线段”,及菱形ABCD易知∠ABD=∠CBD,即BD平分∠ABC.因此,过点G作GM⊥BA于M,作GN⊥BC于N,可得GM=GN,如图2所示,易证Rt△AMG≌Rt△PNG.从而得∠AGM=∠PGN,进而得∠AGP=∠MGN.再由四边形BMGN内角和为360°,易知∠MGN+∠MBN=180°,而∠MBN为定值,从而∠MGN也是定值的.由∠AGP=∠MGN,知∠AGP也是定值.在等腰三角形AGP中,顶角∠AGP不变,其底角∠APG也不变,故选D.
解法二:根据“圆的定义”构造辅助圆.
分析:“由垂直平分线得等线段”,连接GA,由EG垂直平分AP,知GA=GP,再由“菱形的轴对称性”,连接CG,知GA=GC,因此,GA=GP=GC,即A,P,C三点到点G的距离相等,由“圆的定义”知A,P,C三点在以G为圆心,AG长为半径的圆上,因此,构造出辅助圆,如图3所示.由“在同圆中,同弧所对的圆周角等于该弧所对圆心角的一半”,知∠AGP=2∠ACP.因为在菱形ABCD中,∠ACP不变,所以∠AGP不变,进而知∠APG不变,故选D.
感悟:解法二通过线段垂直平分线的性质定理和菱形的轴对称性,结合待解决的问题,巧妙地运用圆的定义,构造辅助圆,运用圆的相关知识找到不变角,进而解决问题.两种解法相比,解法二简单、明了,给人一种顿悟的感觉,让人赏心悦目.
在解几何题中,结合题目条件巧妙地构造辅助圆,建立圆的模型,化繁为简、化难为易、化隐为显,会带领我们走向柳暗花明.但是在解题中,如何构造出辅助圆,这是学生感到困惑的问题,怎样解决学生的困惑将成为教师关注的焦点.笔者将构造辅助圆解几何题归纳出五种类型,与学生、教师共同学习、探究.
二、构造辅助圆的几种类型
圆是一个重要的数学模型,有了圆这个关键载体,其丰富的内涵价值可以直接为我们所用,文章归纳五种构造辅助圆的类型,建立圆的模型,运用圆中的相关结论,巧妙地解决几何问题.
(一)共端点三等线段,“圆”形毕露
图4圆的集合定义:在同一个平面内,到定点O的距离等于定长r的点的集合,其中定点O叫作圆心,定长r叫作半径.由定义可知“圆中半径处处相等”,如图4所示,已知AB=AC=AD,那么我们联想到“圆中半径处处相等”,可巧妙地构造出以A为圆心,AB长为半径的⊙A,AB,AC,AD三条线段有公共端点A,且AB=AC=AD,这种类型称为“共端点三等线段”.下面列举一个案例来分析如何运用“共端点三等线段”构造辅助圆,巧解几何题.
例1 如图5,抛物线y=14x2-32x-4与x轴交于A,B两点,与y轴交于点C,对称轴与x轴交于点M,直线y=x+2与抛物线交于点D,E(D在E的左侧),与抛物线的对称轴交于点F,求∠DCF的大小.
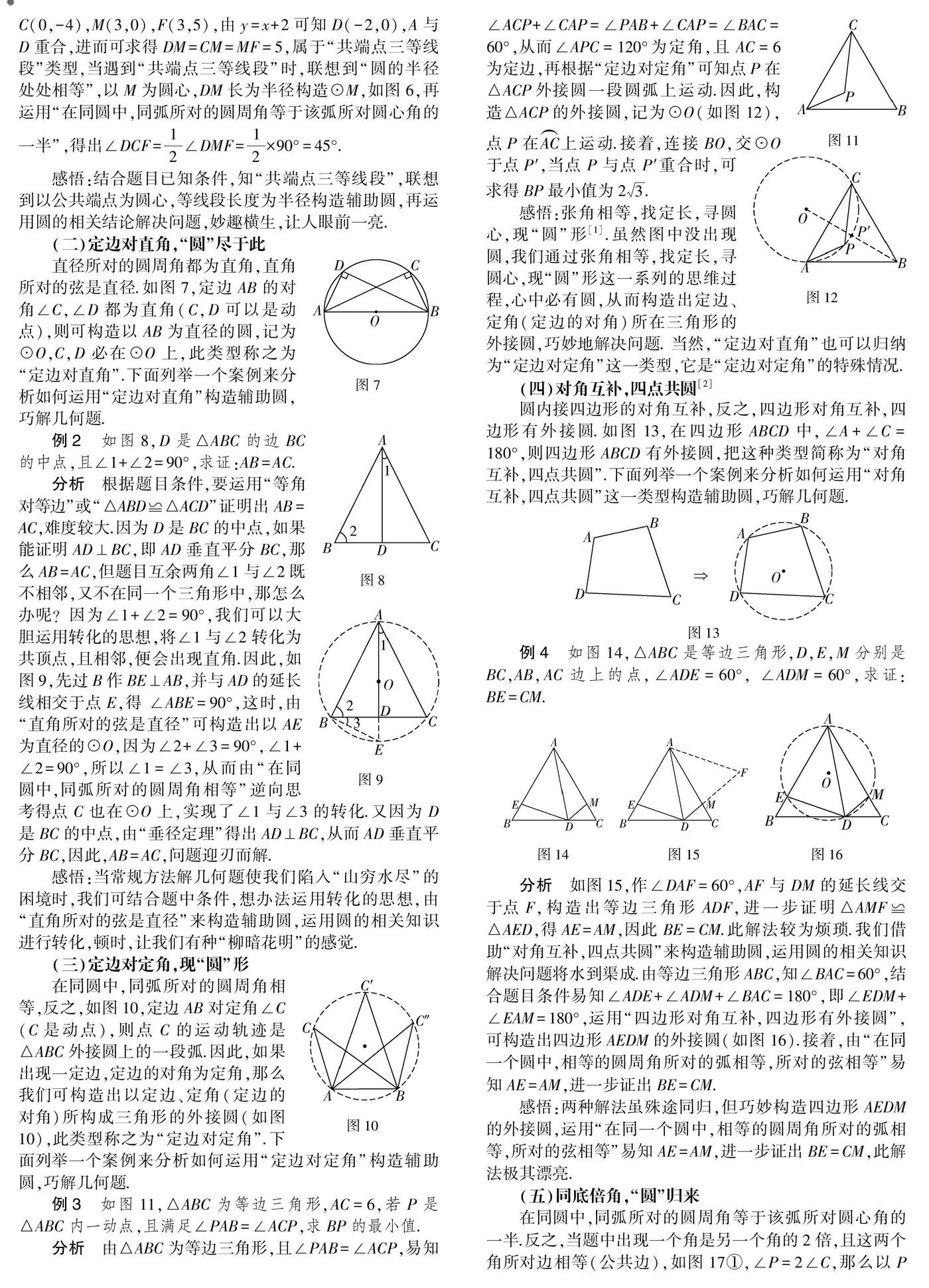
分析 由y=14x2-32x-4易求出A(-2,0),B(8,0),C(0,-4),M(3,0),F(3,5),由y=x+2可知D(-2,0),A与D重合,进而可求得DM=CM=MF=5,属于“共端点三等线段”类型,当遇到“共端点三等线段”时,联想到“圆的半径处处相等”,以M为圆心,DM长为半径构造⊙M,如图6,再运用“在同圆中,同弧所对的圆周角等于该弧所对圆心角的一半”,得出∠DCF=12∠DMF=12×90°=45°.
感悟:结合题目已知条件,知“共端点三等线段”,联想到以公共端点为圆心,等线段长度为半径构造辅助圆,再运用圆的相关结论解决问题,妙趣横生,让人眼前一亮.
(二)定邊对直角,“圆”尽于此
图7直径所对的圆周角都为直角,直角所对的弦是直径.如图7,定边AB的对角∠C,∠D都为直角(C,D可以是动点),则可构造以AB为直径的圆,记为⊙O,C,D必在⊙O上,此类型称之为“定边对直角”.下面列举一个案例来分析如何运用“定边对直角”构造辅助圆,巧解几何题.
图8例2 如图8,D是△ABC的边BC的中点,且∠1+∠2=90°,求证:AB=AC.
分析 根据题目条件,要运用“等角对等边”或“△ABD≌△ACD”证明出AB=AC,难度较大.因为D是BC的中点,如果能证明AD⊥BC,即AD垂直平分BC,那么AB=AC,但题目互余两角∠1与∠2既不相邻,又不在同一个三角形中,那怎么办呢?因为∠1+∠2=90°,我们可以大胆运用转化的思想,将∠1与∠2转化为共顶点,且相邻,便会出现直角.因此,如图9,先过B作BE⊥AB,并与AD的延长线相交于点E,得 ∠ABE=90°,这时,由“直角所对的弦是直径”可构造出以AE为直径的⊙O,因为∠2+∠3=90°,∠1+∠2=90°,所以∠1=∠3,从而由“在同圆中,同弧所对的圆周角相等”逆向思考得点C也在⊙O上,实现了∠1与∠3的转化.又因为D是BC的中点,由“垂径定理”得出AD⊥BC,从而AD垂直平分BC,因此,AB=AC,问题迎刃而解.
感悟:当常规方法解几何题使我们陷入“山穷水尽”的困境时,我们可结合题中条件,想办法运用转化的思想,由“直角所对的弦是直径”来构造辅助圆,运用圆的相关知识进行转化,顿时,让我们有种“柳暗花明”的感觉.
(三)定边对定角,现“圆”形
图10在同圆中,同弧所对的圆周角相等,反之,如图10,定边AB对定角∠C(C是动点),则点C的运动轨迹是△ABC外接圆上的一段弧.因此,如果出现一定边,定边的对角为定角,那么我们可构造出以定边、定角(定边的对角)所构成三角形的外接圆(如图10),此类型称之为“定边对定角”.下面列举一个案例来分析如何运用“定边对定角”构造辅助圆,巧解几何题.
例3 如图11,△ABC为等边三角形,AC=6,若P是△ABC内一动点,且满足∠PAB=∠ACP,求BP的最小值.
分析 由△ABC为等边三角形,且∠PAB=∠ACP,易知∠ACP+∠CAP=∠PAB+∠CAP=∠BAC=60°,从而∠APC=120°为定角,且AC=6为定边,再根据“定边对定角”可知点P在△ACP外接圆一段圆弧上运动.因此,构造△ACP的外接圆,记为⊙O(如图12),点P在AC上运动.接着,连接BO,交⊙O于点P′,当点P与点P′重合时,可求得BP最小值为23.
感悟:张角相等,找定长,寻圆心,现“圆”形[1].虽然图中没出现圆,我们通过张角相等,找定长,寻圆心,现“圆”形这一系列的思维过程,心中必有圆,从而构造出定边、定角(定边的对角)所在三角形的外接圆,巧妙地解决问题. 当然,“定边对直角”也可以归纳为“定边对定角”这一类型,它是“定边对定角”的特殊情况.
(四)对角互补,四点共圆[2]
圆内接四边形的对角互补,反之,四边形对角互补,四边形有外接圆.如图13,在四边形ABCD中,∠A+∠C=180°,则四边形ABCD有外接圆,把这种类型简称为“对角互补,四点共圆”.下面列举一个案例来分析如何运用“对角互补,四点共圆”这一类型构造辅助圆,巧解几何题.
例4 如图14,△ABC是等边三角形,D,E,M分别是BC,AB,AC边上的点,∠ADE=60°, ∠ADM=60°,求证:BE=CM.
分析 如图15,作∠DAF=60°,AF与DM的延长线交于点F,构造出等边三角形ADF,进一步证明△AMF≌△AED,得AE=AM,因此BE=CM.此解法较为烦琐.我们借助“对角互补,四点共圆”来构造辅助圆,运用圆的相关知识解决问题将水到渠成.由等边三角形ABC,知∠BAC=60°,结合题目条件易知∠ADE+∠ADM+∠BAC=180°,即∠EDM+∠EAM=180°,运用“四边形对角互补,四边形有外接圆”,可构造出四边形AEDM的外接圆(如图16).接着,由“在同一个圆中,相等的圆周角所对的弧相等,所对的弦相等”易知AE=AM,进一步证出BE=CM.
感悟:两种解法虽殊途同归,但巧妙构造四边形AEDM的外接圆,运用“在同一个圆中,相等的圆周角所对的弧相等,所对的弦相等”易知AE=AM,进一步证出BE=CM,此解法极其漂亮.
(五)同底倍角,“圆”归来
在同圆中,同弧所对的圆周角等于该弧所对圆心角的一半.反之,当题中出现一个角是另一个角的2倍,且这两个角所对边相等(公共边),如图17①,∠P=2∠C,那么以P为圆心,PA的长度为半径,构造出辅助圆(如图17②),则点C在⊙P上,此种类型称之为“同底倍角”.下面列举一个案例来分析如何运用“同底倍角”构造辅助圆,巧解几何题.
例5 如图18,以△ABC的边AB为底作等腰三角形△PAB,且∠P=2∠C,AC与PB交于点D,若PB=4,PD=3,求AD·DC的值.
分析 题目中出现∠P=2∠C,且PA=PB,∠P与∠C所对的边相同(公共边),可以联想到“在同圆中,同弧所对的圆周角等于该弧所对圆心角的一半”,运用“同底倍角”这一类型来构造辅助圆,如图19,以P为圆心,PB的长度为半径作圆,并延长BP交⊙P于点Q,连接AQ,易知∠C=∠Q,从而得△BDC∽△ADQ,可得BDAD=CDQD,即CD·AD=BD·QD,易知BD=1,QD=7.因此,CD·AD=7.
感悟:本题运用“在同圆中,同弧所对的圆周角等于该弧所对圆心角的一半”,借助“同底倍角”这一类型,构造出辅助圆,运用圆中的知识解决问题,思路精巧,方法独特,但需要注意的是题目恰巧PA=PB,点A在此圆上,又由∠P=2∠C,可知点C也在圆上,其间的细节还有待我们仔细琢磨.
三、“圆”来如此
以上归纳出构造辅助圆解几何题的五种类型,并列举案例分析阐述如何运用相应的类型来构造辅助圆,妙解几何题.现对这五种类型的知識依据做进一步的概括:运用“共端点三等线段”这一类型构造辅助圆主要的知识依据是圆的定义;运用“定边对直角”这一类型构造辅助圆主要的知识依据是直径所对的圆周角都为直角,直角所对的弦是直径;运用“定边对定角”这一类型构造辅助圆主要的知识依据是在同圆中,同弧所对的圆周角相等;运用“对角互补,四点共圆”这一类型构造辅助圆主要的知识依据是对角互补的四边形必有外接圆;运用“同底倍角”这一类型构造辅助圆主要的知识依据是在同圆中,同弧所对的圆周角是该弧所对圆心角的一半.五种类型构造辅助圆,并非无中生有,而是基于学生已扎实掌握圆的相关知识,结合题目已知条件和所要解决的问题进行构造,建立圆的模型,运用圆的相关结论以及其他知识点解决问题.
学生在学习中更需明白其中构造辅助圆的数学原理,知其所以然,真正领会“圆”来如此,才能深知其中的奥妙,做到图中无圆,心中有圆.
【参考文献】
[1]沈岳夫.微专题:道是无“圆”却有“圆”[J].中学数学杂志,2019(06):50-52.
[2]李昌刚.图中无圆,心中构圆:谈中考压轴题巧构辅助圆的策略[J].福建中学数学,2018(06):40-42.

