达到Gilbert-Varshamov 界的准扭码
卢啸华,王永超,丁 洋
(上海大学理学院,上海 200444)
常循环码是循环码的一种推广,具有严谨的代数结构,可以非常容易地进行编码和译码.准循环码是循环码的另一个自然推广,是已渐进好的. 有限域上的准扭码是一类重要的分组码,常循环码和准循环码都是它的特例. Daskalov 等[1]构造了七类三元准扭码,改进了最小距离的下界. Ackerman 等[2]利用准扭码和其对偶码构造了一些新的五元线性码. Aydin 等[3]研究了1-生成准扭码. Saleh 等[4]研究了具有补对偶码的1-生成准扭码.
Gilbert-Varshamov 界是纠错码中一个非常重要的界. 随机码有很大概率达到Gilbert-Varshamov 界. 然而,“是否存在一类达到渐进Gilbert-Varshamov 界的循环码”这一问题尚未得到解决[5-6]. 为了解决这个问题,一些学者开始考虑循环码的变形. Shi 等[7]证明了存在渐进好的加性常循环码. Mi 等[8]证明了一簇指数随码长变化的准循环码是渐近好的.Kasami 等[9]证明了一类信息率为1/2 的二元准循环码可以达到一个比Gilbert-Varshamov 界稍微弱一点的界. Bazzi 等[6]证明了一类随机的二元阿贝尔群码有很大的概率能达到Gilbert-Varshamov 界. Fan 等[10]将Bazzi 等[6]的结论推广到了q元阿贝尔群码. 本工作证明了一类q元准扭码可以达到Gilbert-Varshamov 界.
1 预备知识
1.1 线性码
Fq表示含有q个元素的有限域,Fnq表示Fq上的n维向量空间. 对于任意的x=(x1,x2,··· ,xn)∈Fnq,x的Hamming 重量(用符号wt(x)来表示)被定义为非零分量xi的个数,即
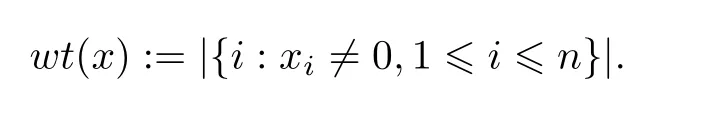
对于任意的x,y ∈Fnq,x和y之间的Hamming 距离d(x,y)被定义为
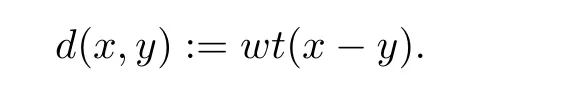
Fnq的非空子集C被称为一个码长为n的q元码,码C的最小距离d(C)被定义为
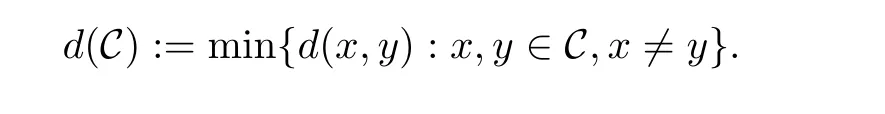
码C的相对最小距离δ(C)和信息率R(C)分别被定义为
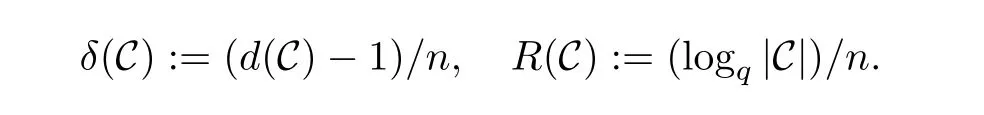
若C是的k维Fq-子空间,则称C是参数为[n,k]的q元线性码. 显然,q元[n,k]线性码C的信息率为R(C)=k/n[11].
定义1(信息集) 设C ⊆是维数为k的线性码. 一个集合A={i1,i2,··· ,ik} ⊆{1,2,··· ,n}称为线性码C的信息集,指C到的投影映射,即

是一个双射.
定义2(平衡码) 一个线性码C被称为平衡码,指存在整数r≥1 和码C的信息集A1,A2,··· ,Au,使得对于任意的i(1 ≤i≤n),有

式中,A1,A2,··· ,Au可以相同.
在0 ≤x≤1-q-1上的q元熵函数Hq(x)被定义为
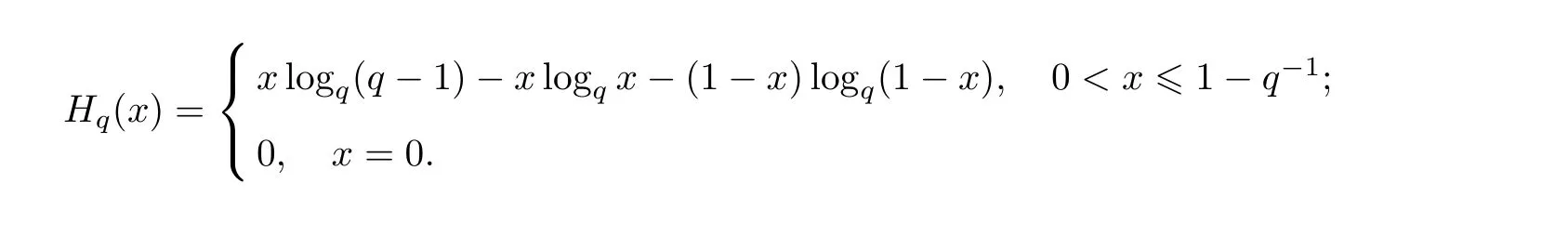
引理1[10]设线性码C是维数为k的平衡码,B是C的一个非空子集. 令
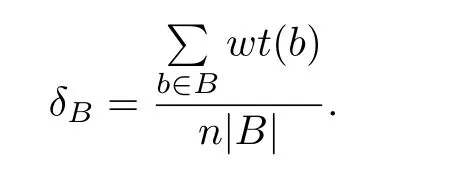
若0 ≤δB≤1-q-1,则
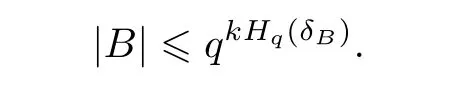
码的各个参数之间存在着彼此制约的关系. 设αq(δ)表示Fq上相对最小距离为δ的q元码的最大信息率. 纠错码的一个主要问题就是确定αq(δ)的值,而渐进的Gilbert-Varshamov 界给出了αq(δ)的一个下界.
命题1(渐进的Gilbert-Varshamov 界)[11]设q≥2. 若0<δ≤1-q-1,则

1.2 准扭码和不可约多项式
Fq[X]表示所有系数在Fq中的一元多项式的全体. 设n,m是两个正整数,且满足m | n,gcd(n,q)=1. 令l=n/m,则对于任意的a ∈Fnq可以写成如下形式:
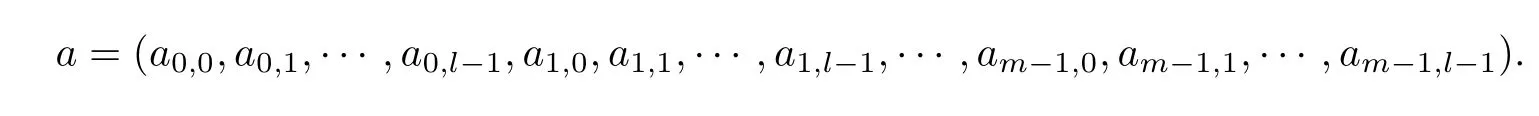
对于任意的λ ∈F*q,令Rm,λ表示剩余类环Fq[X]/(Xm-λ). 由于Fmq和Rm,λ之间存在Fq-线性同构,因此可将向量u= (u0,u1,··· ,um-1)∈和多项式看成是一样的.
定义3(准扭码) 设n,m是两个正整数,且满足m | n,gcd(n,q) = 1. 令l=n/m. 对于任意的λ ∈线性码C被称为(λ,l)-准扭码. 具体指,若
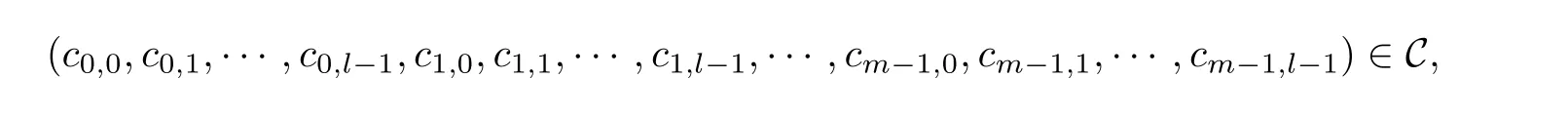
则
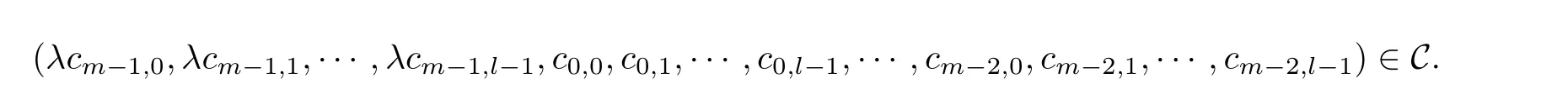
特别地: 当l= 1 时,C恰为λ-常循环码; 当λ= 1 时,C恰为指数为l的准循环码; 当l=λ=1 时,C恰为循环码.
定义映射
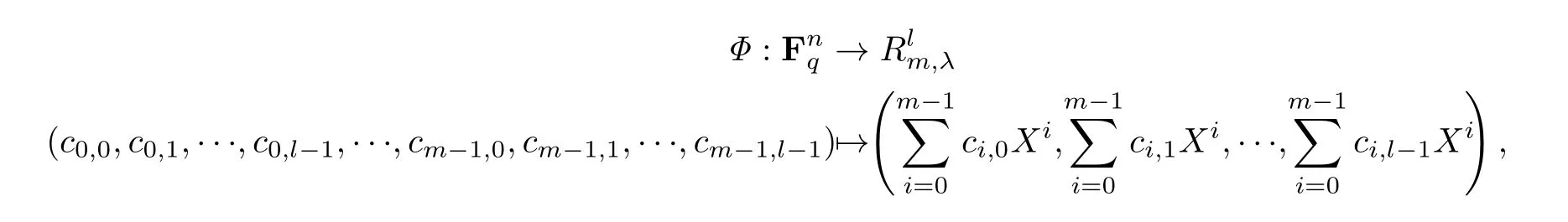
Φ是Fq上的线性同构,且有如下的性质.
命题2设n,m是两个正整数,且满足m|n,gcd(n,q) = 1. 令l=n/m,则对于任意的λ ∈,码C ⊆Fnq是(λ,l)-准扭码当且仅当Φ(C)是的Rm,λ- 子模.
证明 设码C是(λ,l)-准扭码. 由于Φ是Fq上的线性同构,因此对于加法运算、Φ(C)与有限域Fq的数乘运算都是封闭的. 在Rm,λ中Xm=λ,因此对于任意的c ∈C,有

而XΦ(c)对应C中的码字:
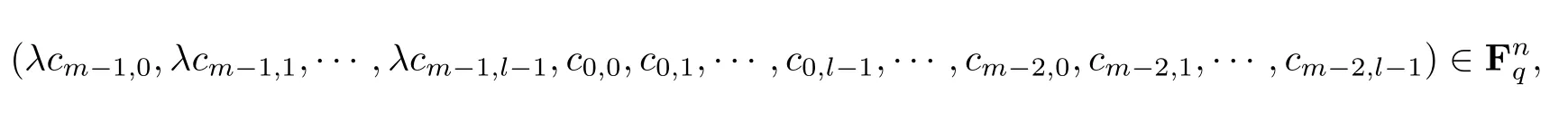
故XΦ(c)∈Φ(C). 因此对于任意的r(X)∈Rm,λ,有r(X)Φ(c)∈Φ(C),即Φ(C)是的Rm,λ-子模.
若Φ(C)是的Rm,λ-子模,则通过上面的讨论可知,C是(λ,l)-准扭码.
定义4(1-生成准扭码) (λ,l)-准扭码C被称为1-生成准扭码,指的Rm,λ-子模Φ(C)是由
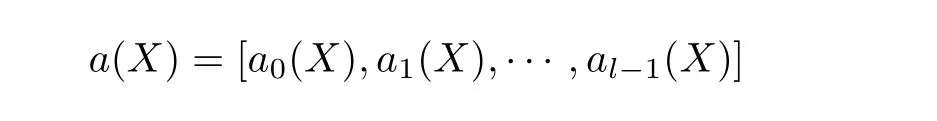
生成的,并且称a(X)为C的生成元.
类似地,也可以定义1-生成准扭码的生成多项式.
定义5设(λ,l)-准扭码C ⊆Fnq是1-生成准扭码,且其生成元是
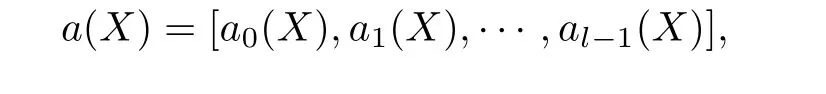
则称
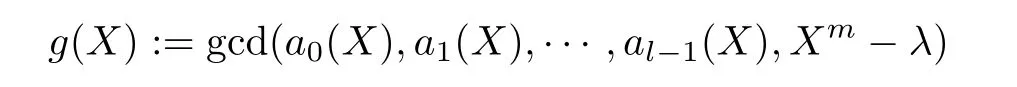
为1-生成准扭码C的生成多项式.
注1若1-生成准扭码C ⊆Fnq的生成多项式是g(X),则C的维数是m-degg(X).
引理2[12]设λ ∈,整数m≥2,则多项式Xm -λ在Fq上是不可约的,当且仅当以下两个条件同时成立: ①设λ在中的阶是e,则m的每个素因子可以整除e,但不能整除(q-1)/e; ②若m ≡0 mod 4,则q ≡1 mod 4.
利用引理2,可以给出下面几个不可约多项式的例子.
(1) 当q= 7 时,设α是的本原元,λ=α2,则对于任意的正整数e,x3e -λ在F7上是不可约的.
(2) 当q= 16 时,设α是的本原元,λ=α5,则对于任意的正整数e,x3e -λ在F16上是不可约的.
(3) 当q= 81 时,设α是的本原元,λ=α5,则对于任意的正整数e,x2e -λ在F81上是不可约的.
2 3 个引理
为了证明任意一个1-生成准扭码有很大概率达到渐进Gilbert-Varshamov 界,先证明一些引理.
因为Fq的特征与m互素,所以多项式Xm-λ在Fq上可以分解成如下形式:
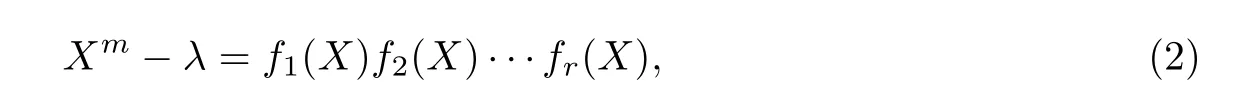
式中,f1(X),f2(X),··· ,fr(X)是不同的不可约多项式. 令dλ=min{degfi(X):1 ≤i≤r}.
引理3设λ ∈F*q. 令a0(X),a1(X),··· ,al-1(X)是从Fq[X]中随机选取的次数小于m的多项式. 当l和m趋向于无穷,且l的增长速度大于logq m时,事件
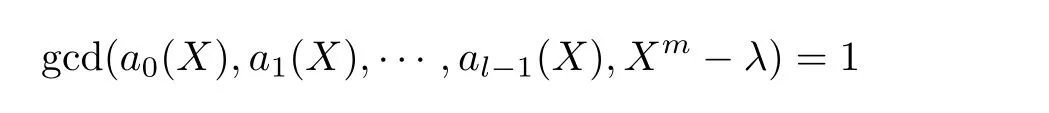
发生的概率趋向于1.
证明 设a0(X),a1(X),··· ,al-1(X)是从Fq[X]中随机选取的次数小于m的多项式,令
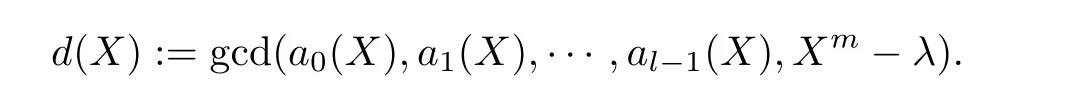
以下证明首一多项式d(X)=1 的概率至少是1-m/ql.
假设degd(X)≥1,则存在Xm-λ的不可约因式f(X),使得f(X)|d(X),即

因为a0(X),a1(X),··· ,al-1(X)是从Fq[X]中随机选取的次数小于m的多项式,所以对于每一个i,f(X)|ai(X)的概率最大为
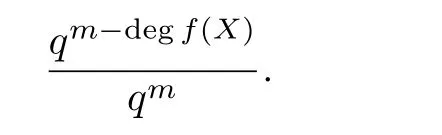
又因为Xm-λ有r个不同的不可约因式,所以degd(X)≥1 的概率最大为
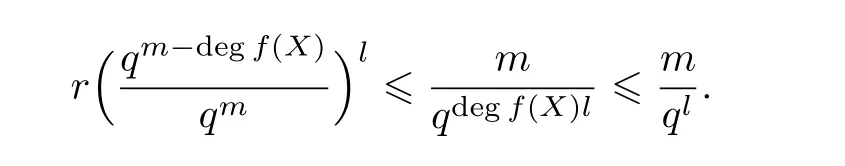
这表明首一多项式d(X)=1 的概率至少为1-m/ql. 当l和m趋向于无穷,且l的增长速度大于logq m时,1-m/ql是趋向于1 的. 引理得证.
设I是Rm,λ= Fq[X]/(Xm -λ)的一个理想. 由于Rm,λ是主理想整环,因此可设I=〈h(X)〉,其中h(X)是首一多项式且h(X)|(Xm-λ),则易知I的维数是m-degh(X).令Ωt表示主理想整环Rm,λ所有维数为t的理想组成的集合. 由文献[6]可以类似地得到如下两个引理.
引理4主理想整环Rm,λ维数为t的理想的个数|Ωt|满足

证明 设I ⊆Rm,λ是Rm,λ维数为t的理想. 因为Rm,λ= Fq[X]/(Xm -λ)是主理想整环,所以存在唯一的首一多项式h(X)满足h(X)|(Xm -λ)和degh(X) =m-t,使得I是由h(X)生成的.
由
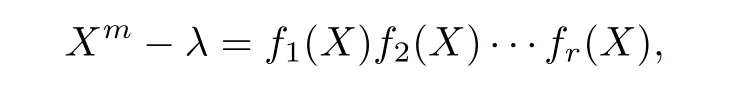
式中,f1(X),f2(X),··· ,fr(X)是不同的不可约多项式,可以得到
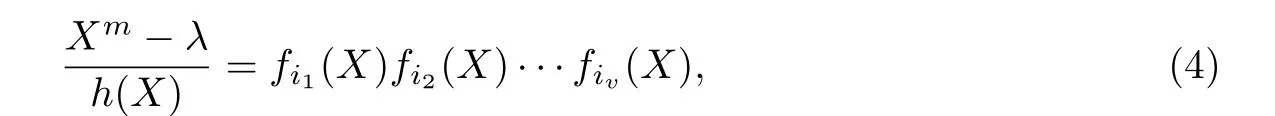
其中fi1(X),fi2(X),··· ,fiv(X)是Xm-λ的不可约因式. 因为degh(X)=m-t,degfij(X)≥dλ(1 ≤j≤v),所以式(2)右端中最多有t/dλ个因式,进而h(X)最多有rt/dλ种选择,故
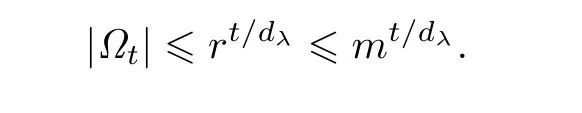
引理得证.
引理5设I是Rm,λ维数为t的理想,w是满足0 ≤w≤(1-q-1)m的整数. 令

有

证明 设I是主理想整环Rm,λ维数为t的理想,则I对应于Fq上一个维数为t的λ-常循环码CI. 设J是CI的一个信息集,定义
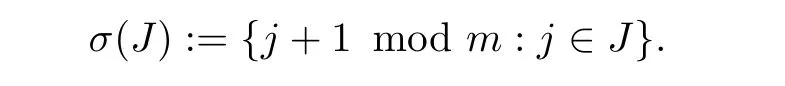
因为CI是一个常循环码,所以σ(J)也是CI的一个信息集. 在信息集{σi(J) : 0 ≤i≤m -1}中,每个i恰好包含在|J|个信息集里,则CI是平衡码. 由引理1 可令B=I(w),,因此
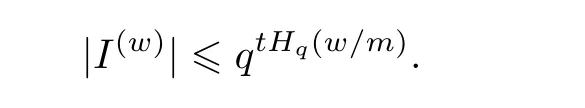
引理得证.
3 达到Gilbert-Varshamov 界的准扭码
利用群环上的群作用,Bazzi等[6]和Fan等[10]证明了准阿贝尔群码可以达到Gilbert-Varshamov 界. 本工作类似地证明了1-生成准扭码也可以达到Gilbert-Varshamov 界. 首先给出这类准扭码的构造.
设
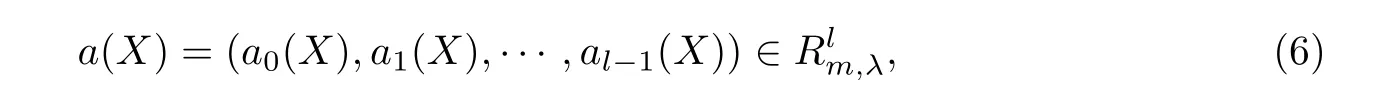
式中,a0(X),a1(X),··· ,al-1(X)是从Fq[X]中随机选取的次数小于m的多项式. 令Ca表示由a(X)生成的码长为n=ml的1-生成(λ,l)-准扭码.
定理1设Ca是由式(6)中a(X)生成的准扭码,且
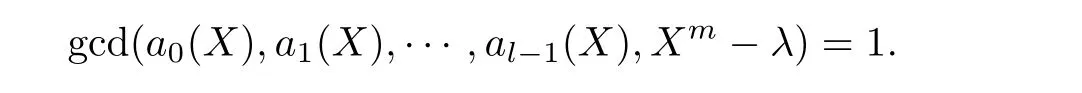
若0<δ≤1-q-1,且
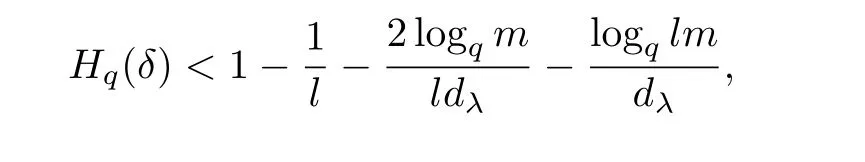
则Ca的相对最小距离小于δ的概率不超过
证明 令P表示准扭码Ca的最小距离小于lmδ的概率. 对于非零多项式f(X)∈Rm,λ,E(f,a)表示事件
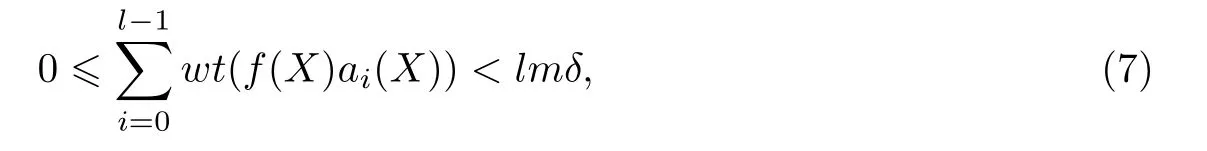
式中,wt(f(X))表示多项式f(X)非零系数的个数,则
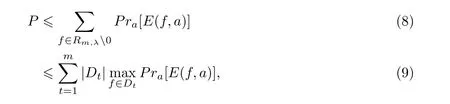
其中Dt:={f(X)∈Rm,λ:deg(gcd(f(X),Xm-λ))=m-t},Pra[E(f,a)]表示事件E(f,a)发生的概率. 对于任意的多项式f(X)∈Rm,λ�,显然有

令Ωt表示主理想整环Rm,λ所有维数为t的理想组成的集合,则
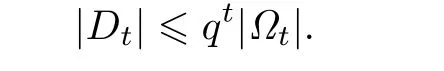
对于任意满足dλ≤t≤m的整数t和任意多项式f(X)∈Dt,令If表示Rm,λ由f(X)生成的理想. 定义

因此有
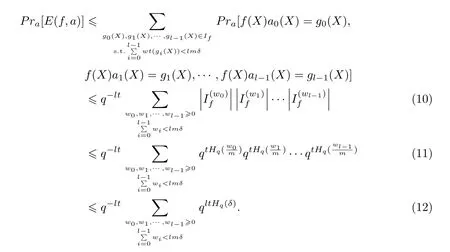
定义一个映射
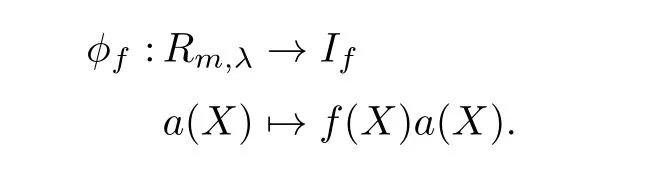
对于任意的g(X)∈If,有

故不等式(10)成立. 由引理5 可知不等式(11)成立. 不等式(12)成立是因为q元熵函数Hq(x)是凸函数.
综上:
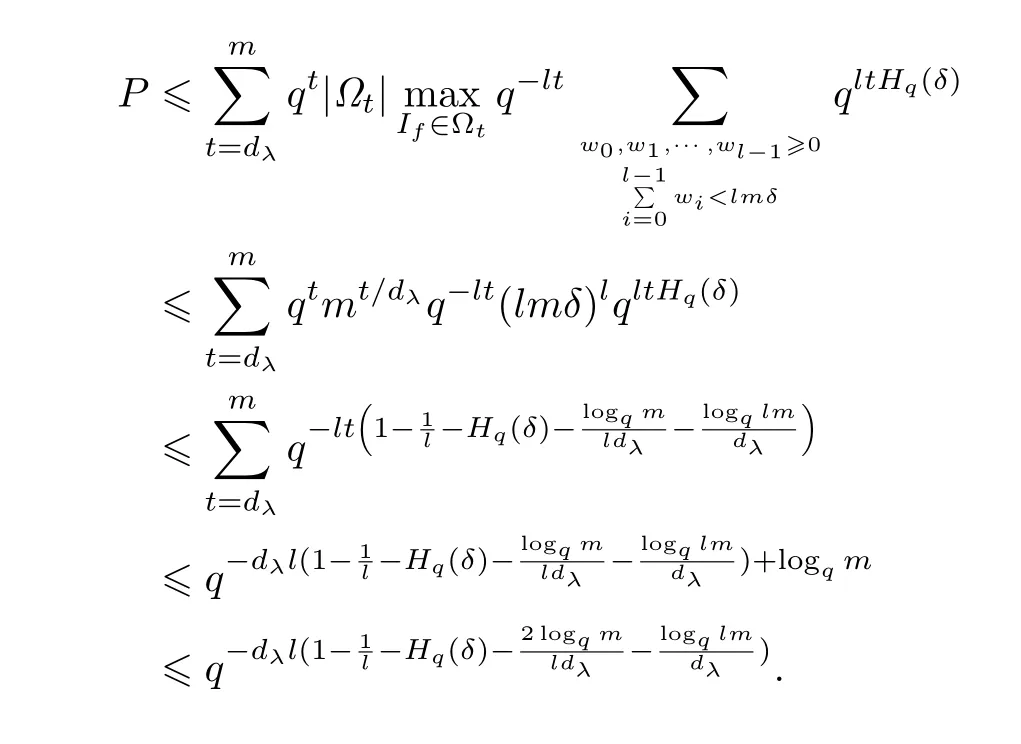
定理得证.
定理2设l,m是两个正整数且满足gcd(lm,q) = 1. 令λ ∈,且1-生成准扭码Ca有如下形式:
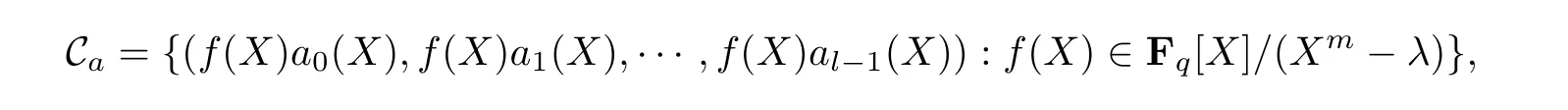
式中,a0(X),a1(X),··· ,al-1(X)是从Fq[X]/(Xm -λ)中随机选取的多项式. 若l和m趋向于无穷,l增长速度大于logq m,且dλ的增长速度大于logq lm,则1-生成准扭码Ca有很大概率达到Gilbert-Varshamov 界,此时Ca的信息率为1/l.
证明 随机选取a(X)=(a0(X),a1(X),··· ,al-1(X))∈. 由引理3 可知,事件
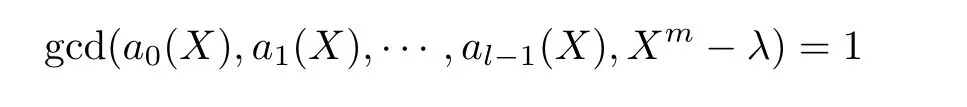
发生的概率趋向于1. 选取满足gcd(a0(X),a1(X),··· ,al-1(X),Xm-λ) = 1 的a(X)生成准扭码Ca,则dimCa=m,此时Ca的信息率为1/l.
由定理1 的讨论可知: 当l的增长速度大于logq m,且dλ的增长速度大于logq lm时,P是非常小的. 因此,Ca的相对最小距离大于或等于δ的概率非常大. 而Ca的信息率为1/l,1/l非常接近1-Hq(δ). 定理得证.
注2(1) 若Xm - λ在Fq上是不可约的,则dλ=m. 令l的增长速度大于logq m,当m趋向于无穷时,dλ的增长速度大于logq lm. 因此,任意的一个1-生成准扭码有很大概率达到Gilbert-Varshamov 界.
(2) 当λ=1 时必有dλ=1,此时无法满足“dλ的增长速度大于logq lm”的条件. 由此可知,本工作的结论对1-生成准循环码并不适用.
下面给出几个1-生成准扭码.
(1) 当q= 7时,设α是的本原元,λ=α2. 令m= 3e,其中e是正整数,则dλ=m.选取正整数l,e且满足l >e,可以构造一类F7上码长为lm的1-生成(λ,l)-准扭码,可渐进达到Gilbert-Varshamov 界.
(2) 当q= 16 时,设α是的本原元,λ=α5. 令m= 3e,其中e是正整数,则dλ=m.选取正整数l,e且满足l >e,可以构造一类F16上码长为lm的1-生成(λ,l)-准扭码,可渐进达到Gilbert-Varshamov 界.
(3) 当q= 81 时,设α是F*81的本原元,λ=α5. 令m= 2e,其中e是正整数,则dλ=m.选取正整数l,e且满足l >e,可以构造一类F81上码长为lm的1-生成(λ,l)-准扭码,可渐进达到Gilbert-Varshamov 界.

