异常值和未知观测噪声鲁棒的卡尔曼滤波器

方安然,李 旦,张建秋

(1.复旦大学电磁波信息科学教育部重点实验室,上海 200433；2.复旦大学电子工程系,上海 200433)

0 引 言

在雷达、声呐、通信、语音识别等应用中,观测中随机出现异常值是一种十分常见的现象[1-2]。例如,无线通信中,电路通断暂态过程产生的脉冲干扰;在雷达或声呐系统中,人为或自然因素产生的冲击性干扰,而引起雷达或声纳观测的随机异常波动等[3]。文献[4]表明:这种观测噪声是非高斯的,其概率密度分布有一个很厚重的“尾部”,因此通常称其为长尾分布/噪声。卡尔曼滤波(Kalman filter,KF)[5],由于其成立的条件是观测噪声为高斯白噪声,因此当观测存在随机异常值时,其性能会显著下降,甚至失效[2,6]。

针对具有随机观测异常值的噪声环境,人们研究了不同的模型方法和滤波算法。就模型方法而言,文献[7]发现:高斯分布与均匀分布的叠加混合,可以反映含异常值观测噪声的“长尾”特性。然而,这种建模方法只适合于观测数据有界的系统。针对观测数据无界的系统,文献[3,8]则分别报道了利用高斯与学生t分布叠加混合,或与拉普拉斯分布叠加混合的模型方法。可是,它们的数学描述都比较复杂,不便于参数估计。为了解决上述问题,文献[2]报道了利用学生t分布来对含异常值的噪声进行建模的方法。但由于其完全依赖于学生t分布,因此有可能无法适应观测噪声可能存在的各种不同分布。

针对非高斯系统的滤波,主要算法有高斯和滤波(Gaussian sum filtering,GSF)[8]和粒子滤波(particle filtering,PF)[7]等。尽管这两种算法能处理非高斯噪声环境中的线性系统滤波问题,但都存在运算复杂度偏高的问题[7]。为了解决这一问题,文献[9]基于新息正交性,提出了一种修正KF (modified Kalman filtering,MKF)算法。尽管这个滤波算法对噪声先验信息是否准确并不敏感,但其收敛过程较慢。针对这一问题,文献[10-11]提出了一类基于相关熵的滤波方法,包括相关熵滤波(correntropy filtering,CF)[10]、修正CF(modified CF,MCF)[11]和最大相关熵KF(maximum correntropy criterion KF,MCC-KF)[11]等方法,加快了算法的收敛速度。不过,其收敛性高度依赖滤波参数选择是否合适。如何选择滤波参数,目前还没有一般性的办法。为此,文献[12]通过引入假设检验,提出了一种自适应鲁棒卡尔曼滤波(adaptive robust KF,ARKF)方法。可由于假设检验需要噪声协方差的准确先验,因此应用受限。为了进一步提高滤波算法的鲁棒性,文献[13]在最小化最大鲁棒估计的准则下,提出了一种中心化融合的鲁棒KF (robust centralized fusion KF,RCFKF)方法。该方法仅适用于未知参数值有界的情况,且估计误差较大。

针对存在观测异常值的线性系统,本文提出了一种新的滤波算法,称之为对异常值鲁棒KF (outlier-robust KF,ORKF)算法。分析表明:当最大后验(maximum a posterior,MAP)准则中加权观测误差的l2范数,用Huber损失函数代替后,就构造了一个新的最优化准则函数。由于Huber损失函数可同时描述l1和l2范数[14],因此借助于这个新的最优化准则函数,本文推导的卡尔曼滤波器就具有了l1范数对异常值的鲁棒性。而当含异常观测值的未知统计分布,利用具有未知参数的高斯混合模型(Gaussian mixture model,GMM)描述时,那么就可根据变分贝叶斯(variational Bayes,VB)的逼近思想,利用贪婪期望最大化(expectation-maximization,EM)算法[15]来对GMM模型中的未知参数进行估计。如此,本文借助于这一思想,进一步提出了对异常值和未知观测噪声同时鲁棒的KF算法,并称其为带VB的ORKF (ORKF-VB)算法。在仿真和实测实验验证分析结果的同时,也展示了提出算法的滤波性能在异常值和观测噪声统计分布未知时,均优于现有文献报道鲁棒卡尔曼滤波类的算法。

1 异常值的统计模型

异常值通常用具有长尾分布特性的非高斯噪声来进行描述[4],这是因为含异常值的随机噪声的分位数-分位数图(quantile-quantile plot,QQ-Plot)在原点附近近似线性,即在均值附近,其分布近似于高斯分布;而在尾部区域,QQ-Plot偏离了线性,那么长的尾部区域就是非高斯分布[16]。位于尾部区域的数据也就称为异常值,它可以描述为一个具有很大方差的零均值高斯分布[16]。这样,包含异常值的观测噪声就可由两个零均值高斯分布构成的GMM来表示,其中一个是背景高斯噪声,另一个就是异常值的统计分布[16]。在一个动态系统中,若vk表示k时刻的随机观测噪声,而p(vk)表示随机观测噪声的概率密度分布,那么就有[16]:

p(vk)=(1-ε)N(vk;0,Σ1)+εN(vk;0,Σ2)

(1)

式中,权值ε是异常值出现的概率,表示了长尾分布的非高斯性,ε越大,该分布的尾部就越“厚”,偏离高斯分布的程度也就越高,反之亦然;N(vk;0,Σ1)表示背景高斯噪声,Σ1是背景高斯分布的协方差;N(vk;0,Σ2)则描述了异常值的高斯分布,Σ2是异常值高斯分布的协方差。

2 KF的回顾

假设一个离散线性系统的状态空间模型[8]为

xk=Fk-1xk-1+wk

(2)

yk=Hkxk+vk

(3)

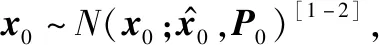
当式(3)中观测不存在异常值时,即观测噪声为高斯白噪声时,KF的预测[7]为

(4)

(5)

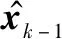
从最大后验的角度,KF算法的状态更新就是最大化了如下函数[15]:

(6)

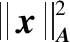
(7)

如此,KF的更新步骤就如下[8]:

(8)

(9)

(10)

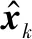
3 对异常值鲁棒的KF

从式(7)中可以发现,其MAP准则采用的损失(评价)函数是l2范数,而l2范数是平方损失函数[14]。当预测/估计值距离真实值越远时,其惩罚力度就越大,这就意味着其对异常值比较敏感。也就是说,l2范数在具有长尾分布的随机噪声环境中容易受到异常值的干扰,甚至有可能导致算法失效。因此,l2范数就不适用于含异常观测值系统的滤波。由文献[14]知,l1范数是利用绝对值的损失函数,相较于l2范数,其对异常值具有更高的鲁棒性。可是,l1范数一般都存在不可导的奇异点,这就为最小化l1范数的计算带来了困难。为此,本文期望通过引入Huber损失函数,在降低异常值对滤波干扰的同时,又可保证处处可导。

Huber损失函数[14]的定义为

(11)

式中,评价函数ρ(·)的定义为

(12)

(13)

式中,A1/2是对称正定矩阵A的Cholesky分解;AT/2是A1/2的转置,满足A=A1/2AT/2;A-1/2是A1/2的逆矩阵;A-T/2是AT/2的逆矩阵。

当将式(7)中第一项用式(11)的Huber损失函数替代时,本文给出了一个新的损失/评价函数如下:

(14)

对式(14)中的xk求导并令该导数等于零,有:

(15)

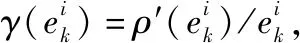
(16)

定义矩阵:

(17)

那么据式(13),就有

(18)

将式(16)～式(18)代入式(15),并利用文献[14,17]中的矩阵恒等式,就有

(19)

这样再将式(13)代入式(19),就可得

(20)

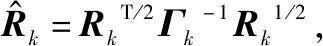
(21)

再整理得

(22)

利用矩阵和求逆公式[18]:

(A-1+BC-1D)-1=A-AB(DAB+C)-1DA

(23)

那么就有

(24)

将式(24)代入式(22),得

(25)

整理得

(26)

再次利用式(23)的矩阵求逆公式,就有

(27)

将式(27)代入式(26),得

(28)

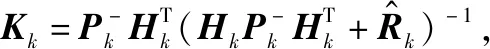
(29)

(30)

(31)

(32)

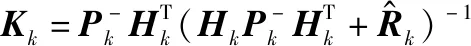
(33)

式(29)和式(33)就是引入Huber损失函数后,状态及其协方差的迭代更新公式,也就是本文提出的ORKF算法,其计算步骤如下。

算法 1 ORKF算法

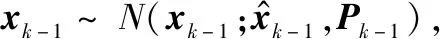
步骤 1预测

(34)

(35)

步骤 2计算尺度函数

(36)

式中,

(37)

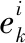
(38)

步骤 3更新

(39)

(40)

(41)

(42)

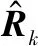
4 参数估计

4.1 利用3σ法则确定Huber函数调谐参数μ

Huber损失函数是一个分段函数,调谐参数μ是它的一个阈值,用于判断观测是否属于异常值。若观测不是异常值,那么Huber函数就是l2范数,最小化式(14)就等价于MAP估计。若观测是异常值,那么Huber函数就是l1范数。在算法中的直观作用就是可依据真实值与预测值之间的归一化残差ek,动态地调整系统模型的观测协方差:归一化残差越大,相应的观测协方差就越大,反之亦然。

判断观测是否属于异常值,一方面取决于观测的真实值与预测值之间的归一化残差向量ek,另一方面取决于调谐参数μ的取值。据式(13)知:归一化残差向量ek与观测方差有关。也就是说,观测yk是否属于异常值同时也取决于观测方差Rk的取值,而Rk则是背景高斯噪声的协方差。

在Huber函数中,调谐参数μ是判断观测是否属于异常值的阈值,残差的绝对值超过此阈值的判定为异常值,低于此阈值的判定为非异常值。据3σ原则:在正态分布中,数值分布在(m-3σ,m+3σ)中的概率约为99.74%,其中m是分布的均值,σ是分布的标准差。因此,对于正态分布,若将调谐参数μ取为3倍标准差,就能很好地判断ek是否来自异常值。由于ek是经过归一化的残差,因此就可取μ=3。

4.2 观测噪声分布未知时的参数估计

本文前面提出的ORKF算法,是针对随机观测噪声分布已知的线性系统。若随机观测噪声的分布未知,那么就需要引入VB的思想,同时对系统的状态和噪声参数做出估计,这就是本文提出的ORKF-VB算法。

据式(1)知随机观测噪声的GMM模型为

p(vk)=(1-ε)N(vk;0,Σ1)+εN(vk;0,Σ2)

(43)

而未知统计分布的随机观测噪声,就指式(43)中异常值出现的概率ε,以及背景高斯噪声和异常值的协方差Σ1和Σ2都未知。

为了估计式(12)和式(43)中的未知参数μ、ε、Σ1和Σ2,本文引入了一种贪婪EM算法[15]。这种算法的优点主要是在提供了一个简便易行参数估计方法的同时,不容易陷入局部极小值,且估计误差比较小。

据文献[17-19]的在线EM算法,对观测序列进行分块处理,以提高参数估计的稳健性。即对观测序列块k=jL-L+1(j=1,2,…,L,其中L是序列块的长度),进行状态估计,并执行贪婪EM算法就可得到当前待求的未知参数。对下一个观测序列块,以上一个观测序列块中估计的未知参数值为初始值再次开始执行EM算法,这样就避免了更新时可能发生较大的异变,也就保证了参数估计的稳健性。

在系统模型式(2)和式(3)中,随机观测噪声的分布未知,也就意味着其参数Rk未知,而Rk则是随机观测噪声中排除异常值后的协方差。由于含异常值的随机观测噪声是一个长尾分布,其在均值附近主要表现为近似于高斯分布的背景高斯噪声,而在远离均值的部分则表现为异常值,因此Rk就是随机观测噪声分布的中心区域背景高斯噪声的协方差。背景高斯噪声的方差小于异常值的方差,而方差实际上就是协方差的迹。因此,在参数估计中,Rk就应更新为迹较小的协方差。如此,本文ORKF-VB算法的流程就如下。

算法2 ORKF-VB算法

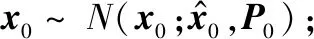
当j=1,2,…,执行以下操作:

步骤 1对时刻k=jL-L+1:jL,执行算法1所示的ORKF算法,得到状态xjL-L+1:xjL的分布,其中L是时间块的长度;

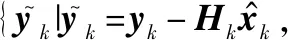
步骤 3更新Rk

(44)

5 仿真实验

本节将进行仿真实验,以验证本文提出的ORKF和ORKF-VB算法的有效性。针对一种基准导航系统的模型[11],本文将比较提出的两种算法与MKF[9]、MCC-KF[11]、ARKF[12]和RCFKF[13]算法的性能。其中,MKF和ARKF算法都是针对异常值问题的经典算法;MCC-KF是相关熵类滤波方法中最新的算法;RCFKF则是针对噪声方差未知的通常算法。

基准导航系统的动态模型可描述[11]为

(45)

(46)

式中,状态变量为

(47)

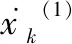
p(vk)=(1-ε)N(vk;0,Σ1)+εN(vk;0,Σ2)

(48)

式中,ε表示异常值出现的概率；Σ1=diag([2,2])是背景高斯噪声的协方差;Σ2=diag([200,200])是异常值的协方差。

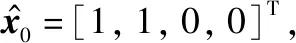
本文将采用目标位置坐标的均方根误差(root mean square error,RMSE)[11]来作为算法性能的评价指标,以衡量滤波结果的准确性。

5.1 不含异常值的仿真

首先来看不含异常值的情况,即异常值出现的概率ε=0。此时,对每一种算法,给定观测噪声的协方差为R=diag([2,2])。仿真结果如图1所示。

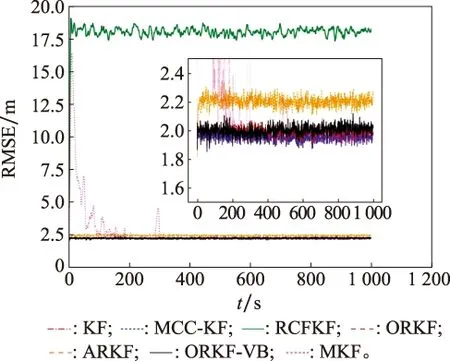
图1 不含异常值的仿真结果Fig.1 Simulation result without outlier

在图1中可以发现,RCFKF算法的RMSE最大,其余6种算法的RMSE都能收敛到2.5 m以下,其中ARKF的RMSE稍大,而MKF算法收敛较慢,而此时本文算法ORKF和ORKF-VB的性能与传统KF的性能相当。

5.2 已知准确噪声协方差的仿真

接下来仿真观测噪声含有异常值的情况,异常值出现的概率ε=0.5。

根据文献[9]和文献[11],MKF和MCC-KF两种算法都是把异常值和背景高斯噪声视为同一个统计分布,因此要求的噪声协方差是异常值与背景高斯噪声混合分布的协方差,据式(1)知,这种非高斯噪声的二阶统计量Σv为

Σv=(1-ε)Σ1+εΣ2

(49)

将ε=0.5,Σ1=diag([2,2],Σ2=diag([200,200])代入式(49),得Σv=diag([101,101])。也就是说,在这个仿真实验中,只有将MKF和MCC-KF算法的噪声协方差给定为R=Σv=diag([101,101])时,才能达到最佳的性能。因此,该方差也就是MKF和MCC-KF算法的准确方差。

根据文献[12],ARKF算法要求的噪声协方差是除去异常值后的背景高斯噪声的协方差,即R=diag([2,2])。

这样,对每一种算法给定正确的噪声协方差即为:对于MKF和MCC-KF算法是R=diag([101,101]),而对于ARKF和本文算法ORKF与ORKF-VB则是R=diag([2,2])。

图2中给出了这些算法在已知准确噪声协方差时的RMSE,可以发现:RCFKF仍是性能最差的一种算法,MKF、MCC-KF和本文算法ORKF与ORKF-VB的RMSE性能则基本相当。不过MKF算法收敛较慢,而ARKF的RMSE算法的性能比上述四者略差。

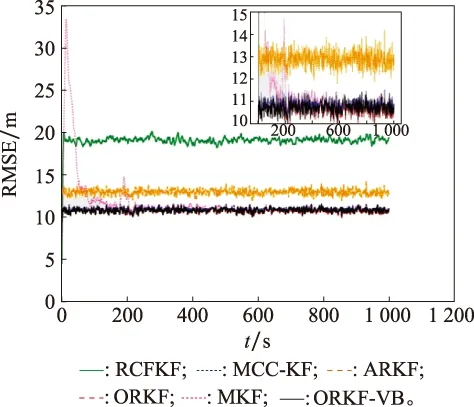
图2 已知准确噪声协方差时的仿真结果Fig.2 Simulation result with correct noise covariance

5.3 噪声协方差存在误差的仿真

在本节的仿真实验中,仍取异常值出现的概率为ε=0.5。然而,这里先验的噪声协方差都存在误差。若给定3组噪声协方差,它们分别是背景高斯噪声协方差的2倍、4倍、10倍,则得到如图3所示的结果。

图3 噪声协方差存在先验误差的仿真1Fig.3 Simulation 1 of a priori error in noise covariance

在图3中,可以发现本文提出的两种算法仍然保持了与图1相近的性能,这表明它们具有很强的鲁棒性。不难发现,MKF仍是收敛最慢的算法,RCFKF仍是性能最差的算法。当给定噪声方差的误差增大到10倍时,ARKF的性能显著变差,表明该算法的鲁棒性差。

当给定的噪声协方差分别是背景高斯噪声与异常值的混合噪声协方差的2倍、4倍、10倍时,全部算法的性能如图4所示。由于此时ARKF算法发散,因此就没有在图4中绘制出其RMSE曲线。

图4 噪声协方差存在先验误差的仿真2Fig.4 Simulation 2 of a priori error in noise covariance

在图4(a)中可以发现,MKF、MCC-KF和本文提出的ORKF-VB算法,收敛后性能几乎相当,但MKF收敛较慢。本文提出的ORKF算法性能稍逊于以上3种算法,这是因为对于ORKF来说,正确的噪声协方差是背景高斯噪声的协方差;而对于MKF和MCC-KF来说,正确的噪声协方差是背景高斯噪声与异常值混合噪声的协方差。因此，对本文提出的ORKF算法而言,始终在利用存在误差的协方差进行估计,且该误差比给出倍数还要大。如图4(a)中给每一种算法的噪声协方差都是混合噪声协方差的2倍,即R=diag([202,202]),它与背景高斯噪声的协方差的差距达101倍,而与混合噪声的协方差的差距仅有2倍,更大的先验误差造成了算法性能更大地下降。而本文提出的ORKF-VB算法尽管最初也使用了错误的协方差,但其在滤波的同时可对噪声协方差进行估计,因此当估计的噪声协方差接近正确后,就能表现出更优的性能。在图4(a)中可以看到,ORKF-VB的RMSE在200 s之前与ORKF极为相近,在200 s之后则明显下降。这是因为ORKF-VB中进行一次高斯噪声协方差估计的观测序列块的长度是L=200,由于观测的时间间隔为Δt=1 s,因此每200 s ORKF-VB算法就对高斯噪声协方差进行一次估计,而200 s则是第一次估计结果改变发生的时刻。因此随着估计参数的不断更新,ORKF-VB算法就获得了越来越准确的噪声协方差,后续的滤波性能也就更好,这一点同样可在图4(b)和图4(c)中发现。

5.4 计算复杂度分析

为了比较这些算法的计算复杂度,对第5.1节中的仿真实验,记录了每一算法运行所需的时间,如表1所示。仿真实验的平台为64位win10操作系统,内存8 GB,Intel处理器,内核i7-4790,CPU 3.6 G,IDLE为Python 3.8。

表1 算法运行时间比较Table 1 Algorithm run time comparison ms

在表1中,本文算法ORKF的平均运行时间高于KF、RCFKF和MKF,而低于ARKF和MCC-KF。本文算法ORKF-VB的平均运行时间远远高于其他所有算法,这是因为多了协方差估计的步骤,这表明该算法的高鲁棒性能是以更高的计算复杂度为代价的。

6 实际验证

本节将以锂电池荷电状态监测问题为例,进行实际验证,以证明本文算法的有效性。针对该问题,本文利用文献[21]提出的一种描述锂电池具有时变内阻和开路电压滞回的系统模型,对锂电池荷电状态(state of charge,SOC)进行估计。与第5节相同,本节将比较提出的两种算法与KF[5]、MKF[9]、MCC-KF[11]、ARKF[12]和RCFKF[13]算法的性能。

文献[21]给出的电池模型如图5所示。在图5中,电池的容量Cn、电池内阻R0、R1和C1、R2和C2构成的2个RC网络都是电池的内部参数;1V·Z表示电池电量,其中Z表示锂电池的SOC;I表示流过电池的电流,充电时为正,放电时为负;VOC(Z)表示电池的开路电压。

图5 锂电池等效电路模型Fig.5 Equivalent circuit model of lithium-ion battery

文献[21]描述锂电池状态的系统模型为

(50)

Vk=VOCA,k+VH,k+R0,kIk+V1,k+V2,k+vk

(51)

式中,Zk是k时刻电池的SOC;V1,k和V2,k反映了k时刻电池所同时具有的短和长时间常数的动态特性;R0,k表示k时刻电池的内阻;Ik表示k时刻流过电池的电流;状态变量xk=[Zk,V1,k,V2,k,R0,k]T;Vk表示电池两端的电压;VOC(Z)=VOCA,k+VH,k是k时刻电池的开路电压,由Zk及电池的充放电状态决定,文献[21]给出了其与Zk之间的函数关系;wk是状态转移噪声,vk是随机观测噪声。在电子电路中,存在热噪声、散弹噪声、粉红噪声等多种随机噪声[22],而电路通断产生的脉冲及外部干扰等又易引起观测的异常波动,因此随机观测噪声中极有可能含有异常值且其分布未知。

实验中使用了一种锂离子聚合物电芯LGABF1L18650电池,额定容量3 350 mA·h,额定电压3.7 V。电压Vk和电流Ik的数据由BQ40Z50芯片实际采集,采样周期为1 s。所有实验均在25℃下进行。实验中电池模型参数R1=0.001 Ω,C1=618 F;R2=0.025 7 Ω,C2=707.7 F。模型参数的确定方法及电容Cn的更新方法由文献[21]给出。电池SOC的真实值是通过改进的安时积分法计算获得的[23]。实验中,MKF、MCC-KF、ARKF的参数设定分别与文献[9]、文献[11]、文献[12]中状态估计误差最小的方法相同;对于所有的算法,状态转移噪声和观测噪声的相关参数均由文献[21]给定。

实验结果如图6和表3所示。图6(a)显示了采用SOC估计的绝对误差。图6(b)显示了不同SOC区间内的平均相对误差,其中SOC区间的划分方法由文献[24]给出,如表2所示。表3则给出了不同方法估计SOC的均方根误差RMSE。

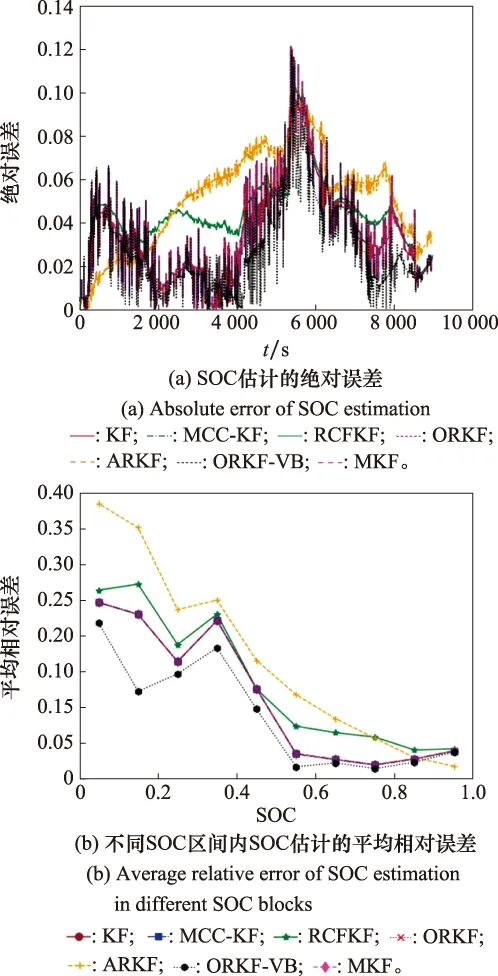
图6 锂电池SOC估计的实验结果Fig.6 Experimental result of SOC estimation of lithium-ion battery

表2 SOC区间划分Table 2 Partition of SOC blocks

表3 锂电池SOC估计的RMSETable 3 RMSE of SOC estimation of lithium-ion battery

图6(a)显示了SOC估计的绝对误差,图6(b)显示了不同SOC区间内的平均相对误差。从图6(b)中可以看到,ARKF性能受SOC区间的影响最明显,当SOC在0.9～1范围内时性能最好。然而,随着SOC逐渐减小,ARKF的相对估计误差就急剧增大。KF、MKF、MCC-KF及本文算法ORKF的性能相差无几,其在各个SOC区间内的相对误差都小于RCFKF,同时又都大于本文算法ORKF-VB的相对误差。在表3中,本文算法ORKF-VB具有最小的RMSE。综上,在锂电池SOC估计问题中,本文算法ORKF-VB是性能最佳的估计方法。

7 结 论

针对存在异常观测值和/或未知观测噪声环境中的线性动态滤波问题,本文利用Huber损失函数代替推导卡尔曼滤波器MAP准则中观测误差的l2范数,构造了一种新的准则函数,并由此推导出了一种ORKF算法。由于Huber函数兼顾了l1范数的鲁棒性,由此本文推导出的卡尔曼滤波器对异常值具有鲁棒性。

当观测噪声分布未知时,本文将噪声建模为具有未知参数的GMM,并依据VB思想,引入一种贪婪EM算法,进一步提出了ORKF-VB算法。

仿真验证和实际验证证明了本文分析结果的有效性。同时也表明:在含异常值和统计分布未知的观测噪声环境中,本文提出算法性能优于现有文献报道的鲁棒类KF算法。