极值点偏移问题解题策略的探究

广东省揭阳市第二中学(515500) 杨邦彬

图1

1.如图1, 假设函数f(x)的图象的顶点的横坐标(即极值点)为x0,若f(x) =c的两根的中点刚好满足=x0, 即极值点在两根的正中间, 也就是说极值点没有偏移.此时函数f(x)在x=x0(附近)两侧的函数值变化快慢相同.

图2

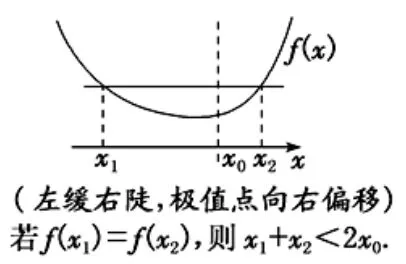
图3

查阅有关文献,在极值点偏移问题中,文[1]介绍极值点偏移的判定定理,并通过具体的例子介绍极值点偏移的解题方法;文[2]给出“和”型极值点偏移问题的统一解法;文[3]介绍了解决问题的四个步骤,让学生能够很好地按部就班进行逻辑推理.让高中学生能够理解与掌握解题的策略与通法,是极值问题教学值得研究的课题.为此,本文基于数学核心素养下学生审题能力提高的策略探究,把极值点偏移问题的解题策略归纳为三种题型进行探究: (1)对称变换;(2)分离零点(极值点);(3)比(差)值换元.然后从引导学生运用导数研究简单函数的性质和变化规律、培养学生会用导数解决实际问题能力的视角,分类分析,循序渐进,一题多解,发挥学生的学习主动性,激发学生的学习动机,基于数学核心素养下, 探究归纳适合高中学生理解与掌握的有效策略与通法,提高学生的审题能力.

策略一 对称变换

策略探究对称变换,主要用来解决与两个极值点之和相关的不等式的证明问题.其解题要点如下:

(1)定函数(极值点为x0),即利用导函数符号的变化判断函数单调性,进而确定函数的极值点x0.

(2)构造函数, 即根据极值点构造对称函数F(x) =f(x)−f(2x0−x).

(3)判断单调性,即利用导数讨论F(x)的单调性.

(4)比较大小, 即判断函数F(x)在某段区间上的正负,并得出f(x)与f(2x0−x)的大小关系.

(5) 转化, 即利用函数f(x) 的单调性, 将f(x) 与f(2x0−x) 的大小关系转化为x与2x0−x之间的关系,进而得到所证或所求.

提醒若要证明的符号问题,还需进一步讨论与x0的大小,得出所在的单调区间,从而得出该处导数值的正负.

典例1(2016年高考新课标Ⅰ卷理数第21 题)已知函数f(x)=(x −2)ex+a(x −1)2有两个零点.

(Ⅰ)求a的取值范围;

(Ⅱ)设x1,x2是f(x)的两个零点,证明:x1+x2＜2.

审题点拨本题待证不等式中含有两个变量,对于此类问题的求解思路是通过两个变量之间的关系“减元”,构造对称函数F(x) =f(x)−f(2x0−x),然后根据函数的单调性,最终将问题转化为函数的最值问题来求解.考查了逻辑推理、数学建模及数学运算等核心素养.在求解此类问题时,需要注意变量取值范围的限定,如本题中利用x1,2−x2的取值范围,利用函数f(x)在(−∞,1)上的单调性来求解.

解题观摩(Ⅰ)a的取值范围是(0,+∞).(过程从略)

(Ⅱ)由(Ⅰ)知,函数f(x)在(−∞,1)单调递减,在(1,+∞)单调递增.令g(x)=f(x)−f(2−x)=(x −2)ex+xe2−x,x ＞1,则2−x ＜1.所以g′(x) = ex+(x −2)ex+e2−x −xe2−x= (x −1)(ex −e2−x)＞0.所以g(x)在(1,+∞)单调递增, 所以g(x)＞g(1) = 0.不妨设x1＜1,x2＞1, 则g(x2)＞0, 即f(x2)＞f(2−x2), 因为f(x1) =f(x2), 所以f(x1)＞f(2−x2),因为函数f(x)在(−∞,1)单调递减,又x2＞1,则2−x2＜1,又x1＜1,所以x1＜2−x2,即x1+x2＜2,得证.

典例2(河北省衡水中学2020 届高三年级下学期三调第21 题)已知函数f(x)=xlnx −+(m −1)x+m有两个极值点x1,x2,且x1＜x2.

(Ⅰ)求实数m的取值范围;

(Ⅱ)若t≥1,证明x1+tx2＞t+1.

审题点拨本题的第(Ⅱ) 小题初看并不是严格的“x1+x2”形式, 但跟两个零点之和相关, 只是多了一个参数t≥1,审题时要注意消参减元,可利用t和x2的范围对式子进行放缩,从而达到消参减元的目的,这是解题的关键.最终化为x1+x2＞2,用策略一构造函数就能顺利解决.

解题观摩(Ⅰ)实数m的取值范围为(1,+∞).(过程从略)

(Ⅱ) 证明: 由(Ⅰ) 知x1∈(0,1), 所以lnx1＜0,x2∈(1,+∞),所以当t≥1 时,x1+tx2=x1+x2+(t −1)x2＞x1+x2+t −1, 所以要证x1+tx2＞ t+ 1, 只需证x1+x2+t −1＞t+1,即x1+x2＞2.证明如下:

令φ(x) =g(x)−g(2−x), 0＜x ＜1.所以φ(x) =lnx−x+m−[ln(2−x)−(2−x)+m]=lnx−ln(2−x)−2x+2,−2=＞0,所以φ(x)在(0,1)上单调递增,又φ(1)=0,所以φ(x)＜0.因为x1∈(0,1), 所以g(x1)−g(2−x1)＜0, 即g(x1)＜g(2−x1), 又g(x2) =g(x1), 所以g(x2)＜g(2−x1).因为x2＞1,x1∈(0,1), 所以2−x1＞1, 因为g(x)在区间(1,+∞)上单调递减,所以x2＞2−x1,即x1+x2＞2.所以x1+tx2＞t+1 成立.

策略二 分离零点(极值点)

策略探究分离零点的主要目的就是减元,进而建立与所求解问题相关的函数.主要是利用函数零点(极值点)乘积所满足的条件进行消参减元.其解题要点如下:

(1)分离零点(极值点),根据两个极值点之积的关系,化简或转化所求解问题,进行消参减元.

(2)构造函数,根据分离零点(极值点)后的式子结构特征,构建相应的函数.

(3) 求解问题, 利用导数研究所构造函数的单调性、极值、最值等,从而解决相关问题.

典例3已知函数f(x)=lnx −ax(a ∈R).

(Ⅰ)求函数f(x)的单调区间;

(Ⅱ)当a= 1 时,方程f(x) =m(m ＜−2)有两个相异实根x1,x2,且x1＜x2,求证:x12.

审题点拨本题第(Ⅱ)问要证明的方程根之间的不等式关系比较复杂,此类问题可通过不等式的等价变形,将两个根分布在不等式两侧,然后利用函数的单调性转化为对应函数值之间的大小关系即可.显然构造函数的关键仍然是消掉参数,确定x2的范围之后才能将x1与化归到函数的同一个单调区间上,这也是此类问题的一个难点——精确定位.

解题观摩(Ⅰ)当a≤0 时,f(x)在(0,+∞)上单调递增;当a ＞0 时,f(x)在上单调递增,在上单调递减.(过程从略)

(Ⅱ)证明: 由题意及(Ⅰ)可知,方程f(x) =m(m ＜−2)的两个相异实根x1,x2满足lnx −x −m= 0, 且0＜x1＜1＜x2, 即lnx1−x1−m= lnx2−x2−m= 0.由题意, 可知lnx2−x2=m ＜ −2＜ln 2−2, 又由(Ⅰ) 可 知,f(x) = lnx −x在(1,+∞) 上单调递减, 故x2＞2.令g(x) = lnx −x −m, 则g(x)−+3 lnx −ln 2.令h(t) =−t++3 lnt −ln 2,t ＞2,则h′(t) =当t ＞2 时,h′(t)＜0,h(t) 单调递减, 所以h(t)＜h(2) = 2 ln 2−＜0, 所以g(x)＜因为x2＞2 且g(x1) =g(x2), 所以g(x2)−=g(x1)−＜0, 即g(x1)＜因为g(x)在(0,1)上单调递增,所以x1＜故

典例3 变式已知函数f(x)=lnx −ax(a ∈R)有两个零点x1,x2,求证:x1x2＞e2.

审题点拨形如x1x2＞x20的不等式, 可构造函数F(x) =f(x)−本题要证的不等式是两个零点积的形式, 可考虑分离零点(极值点), 将两个零点(极值点)视为变量,构造相关函数.判断两个零点的取值范围是关键之处,确定其范围之后才能将x1与化归到函数的同一个单调区间上.这体现了对数学建模等核心素养的考查.(解答从略)

策略三 比(差)值换元

策略探究比(差)值换元的目的是消参、减元,就是根据已知条件首先建立极值点之间的关系,然后利用两个极值点之比(差)作为变量,从而实现消参、减元的目的.设法用比值或差值(一般用t表示)表示两个极值点,继而将所求解问题转化为关于t的函数问题求解.

典例4(2019年金太阳高二期末联考(理)第21 题)已知f(x)=xlnx −−x,m ∈R.若f(x)有两个极值点x1,x2,且x1＜x2.求证:x1x2＞e2(e 为自然对数的底数).

审题点拨求解本题的关键点有两个: 一是消参,把极值点转化为导函数零点之后,需要利用两个变量把参数表示出来,这是解决问题的基础,若只用一个极值点表示参数,如得到m=之后,代入第二个方程,则无法建立两个极值点的关系,本题中利用两个方程相加(减)之后再消参,巧妙地把两个极值点与参数之间的关系建立起来;二是减元,即减少变量的个数,只有把方程转化为一个“变量”的式子后,才能建立与之相应的函数,转化为函数问题求解.本题利用参数m的值相等建立方程,进而利用对数运算的性质,将方程转化为关于的方程,通过建立函数模型求解该问题,这体现了对数学建模等核心素养的考查.

解题观摩欲证x1x2＞e2,只需证lnx1+lnx2＞2.由函数f(x) 有两个极值点x1,x2, 可得函数f′(x) 有两个零点, 又f′(x) = lnx −mx, 所以x1,x2是方程f′(x) = 0 两个不同实根.于是有

两式相加, 可得lnx1+lnx2=m(x1+x2), 即m=两式相减,可得lnx2−lnx1=m(x2−x1),即m=从而可得于是lnx1+lnx2=

由0＜ x1＜ x2, 设t=则t ＞1.因此lnx1+lnx2=,t ＞1.要证lnx1+lnx2＞2,即证＞2,即证当t ＞1 时,有lnt ＞令h(t)=lnt −则＞0, 所以h(t) 在(1,+∞) 上单调递增.因此h(t)＞h(1) = 0.于是当t ＞1 时, 有lnt ＞所以有lnx1+lnx2＞2 成立,即x1x2＞e2.

典例5已知x1,x2是函数f(x)=ex −ax的两个零点,且x1＜x2.

(Ⅰ)求证:x1+x2＞2; (Ⅱ)求证:x1x2＜1.

审题点拨求解本题的关键点仍然是消参、减元,考虑到函数中含有ex,适合作差值换元,将要证明的式子作等价变换,变形出含有“x2−x1”的式子,从而换元,构造出一个新函数,再判断新函数的单调性,利用单调性证明不等式.

解题 观摩(Ⅰ) 问题可以转化 为y=g(x) =xe−x与y=有两 个交点, 又g′(x) =易知g(x) 在(−∞,1)上单调递增, 在(1,+∞)上单调递减, 由x1＜x2,所以0＜ x1＜1＜ x2且

两式相加, 得a=两式相减, 得a=所以故要证x1+x2＞2, 即证变形为令t=x2−x1＞0, 则只需证t(et+1)−2(et −1)＞0.设g(t) =t(et+1)−2(et −1),t ＞0,则g′(t) =tet −et+1,g′′(t) =tet ＞0, 所以g′(t) 在(0,+∞) 上单 调递增, 即g′(t)＞g′(0) = 0.所以g(t) 在(0,+∞) 上单调递增, 即g(t)＞g(0)=0,所以x1+x2＞2.

(Ⅱ) 要证x1x2＜1, 即证＜1, 等价于ex1ex2＜也即等价于令t=x2−x1＞0,等价于等价于等价于−et+ 1＜0.令h(t) =−et+ 1, 则h′(t) =令φ(t)=1+则所以φ(t)在(0,+∞)上单调递减,所以φ(t)＜φ(0) = 0,从而h′(t)＜0,h(t)在(0,+∞)上单调递减,所以h(t)＜h(0)=0.所以x1x2＜1.

本题第(Ⅰ) 问是x1+x2的形式, 也可用“策略一对称变换”解决, 但需先化为y=g(x) =xe−x与y=两个函数, 确定x1,x2的取值范围, 再设y=g(x) 的轴对称函数y=g(2−x), 从而构造函数h(x) =g(x)−g(2−x)来解决.第(Ⅱ) 问可用“策略二分离零点”, 即构造函数φ(x)=g(x)−来解决.读者可自行完成.

探究感悟著名教育家波利亚(Polya)认为,中学数学教育的根本目的是“教会学生思考”[4].极值点偏移问题的本质是函数值变化快慢的问题,是导数在函数研究中的具体应用.基于数学核心素养下学生审题能力提高的策略探究,让考生有较好的思路和途径解决问题.在教学中,教师可以从具体、计算量小的函数模型出发,认真审题,找出问题的结构特征,采用相应的解题策略,引导学生理解掌握极值点偏移的解题策略与通法,方向就是消参减元.循序渐进地训练学生分析问题,构造函数,通过导数研究函数性质,解决实际问题.让学生体会数学学习的成就感,激发学生学习数学的兴趣,促进学生数学核心素养的提升.