一类三次多项式混沌映射的判定及性能分析

臧鸿雁 韦心元 袁 悦

(北京科技大学数理学院 北京 100083)

1 引言

混沌作为一门新兴的学科，一直是学者的重要研究对象。1975年，数学家李天岩和其导师约克(Yorke)建立了“周期三意味着混沌”的判别定理(Li-Yorke混沌判别定理)[1]，为研究1维离散混沌系统提供了理论依据[2]。

由于混沌系统具有初值敏感性、遍历性、类随机性等诸多基本特性，混沌系统和密码学之间存在许多相似之处，这也促使不少学者致力于研究基于混沌的密码算法[3,4]。目前，基于混沌系统生成统计性能良好的混沌伪随机数已经是混沌密码学中的热门研究之一。其中，伪随机序列的均匀性[5]、随机性[6]、复杂度[7]等性能是衡量序列优劣的重要指标。

众所周知，除了Tent映射具有好的均匀性外，其他大部分映射的均匀性并不理想[8]。而2次多项式映射和Tent映射在某些条件下是拓扑共轭的，文献[9]给出了一般2次多项式在满足b2−4ac −2b=8的条件下与Tent映射拓扑共轭的结论。针对这类2次多项式映射，在保证其与Tent映射拓扑共轭的前提下，只要找到二者之间的桥函数，就能获得2次多项式混沌系统的概率密度函数，从而利用一个变换，将不均匀的混沌序列变为均匀的混沌序列[10]，或者依赖2次多项式混沌系统概率密度函数的形式，获取使得混沌系统产生的值以等概率落入不等分区间的区间分点表达式，从而设计出产生独立同分布的混沌密钥流的量化方法[11,12]。可见，利用2次多项式映射和Tent映射的拓扑共轭关系，学者已经取得了丰硕的研究成果。

然而，除了Chebyshev映射外，关于3次多项式映射拓扑共轭的研究却鲜有报道[13,14]。本文首先引入一个具有均匀分布特性的分段线性混沌映射，给出了这个映射与一般3次多项式映射拓扑共轭的充分条件。并进一步对分段线性映射和多项式映射的均匀性、结构复杂性、随机性进行了对比分析。

2 多项式混沌映射

首先，介绍Li-Yorke混沌判别定理，该定理的表述如下。

引理1[1]设J 是一个闭区间，且设f :J →J是连续的，假设存在一点 a ∈J ，使得b =f(a),c=f(b) , d =f(c) 满 足d ≤ab>c)，则f是Li-Yorke意义下的混沌映射。

2.1 分段线性混沌映射

文献[9–12]中，在研究2次多项式映射和Tent映射的拓扑共轭关系时，所用的Tent映射及其分布密度表达式为

为研究3次多项式映射的混沌判定，本文首先引入式(2)所示的分段线性映射 T3。容易验证，映射T3满 足引理1，即T3是Li-Yorke意义的混沌映射。

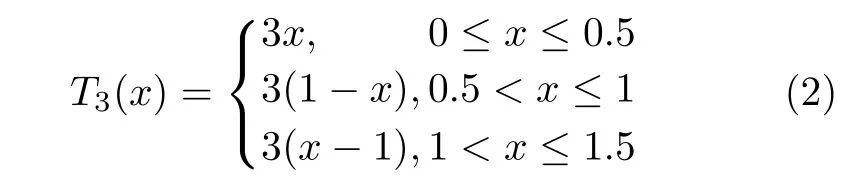
图1(a)和图1(b)分别为映射 T3的函数图像和样本概率密度拟合图。其Lyapunov指数为 λ =ln 3。与Tent映射类似，映射T3服从[0, 3/2]上的均匀分布。

2.2 3次多项式映射的混沌判

为了研究3次多项式系统与映射 T3的拓扑共轭关系，先给出拓扑共轭定义。

定义1[15]设f :X →X 和g :Y →Y是两个映射，若存在同胚 h:X →Y ，满足h ◦f =g ◦h，则称f 和g 关于h 拓扑共轭。

映射 T3和3次多项式的拓扑共轭关系由以下定理描述。

定理1对于一般3次多项式f(x)=ax3+bx2+cx+d 和映射T3。若满足条件

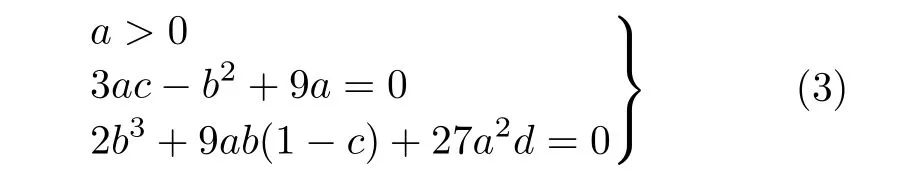
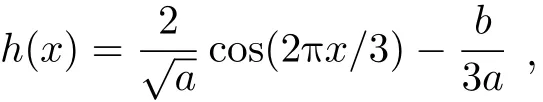
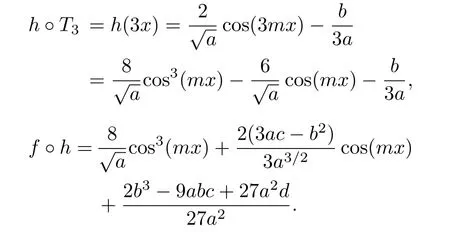
若h ◦T3=f ◦h ，则有

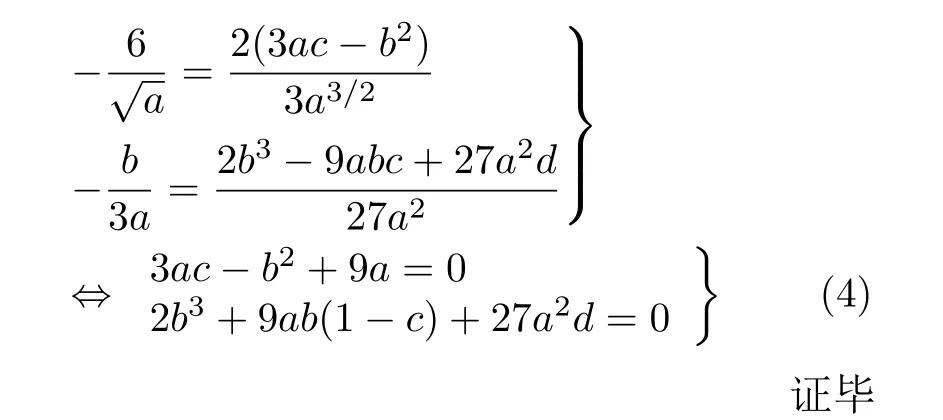
定理1给出了一般3次多项式映射和映射T3拓扑共轭的充分条件。因此，当条件式(3)成立时，3次多项式在Li-Yorke意义下是混沌的。容易验证，众所周知的3阶Chebyshev多项式映射f(x)=4x3−3x满足本文定理1所提出的条件式(3)，也就是说，3阶Chebyshev多项式映射属于定理1所描述的这类混沌系统。

2.3 3次多项式映射的概率密度

图1 映射T 3拟合图

由3次多项式映射与映射 T3的拓扑共轭关系，容易得到3次多项式映射的概率密度函数，见定理2。下面，先给出以下引理2。

引理2[15]如果映射 f , g 和h 满足h ◦g =f ◦h，即 f 和g 关 于h 拓 扑 共 轭，且ρg(x) 是 映 射g 的 概 率 密度函数，则映射f 的概率密度函数为

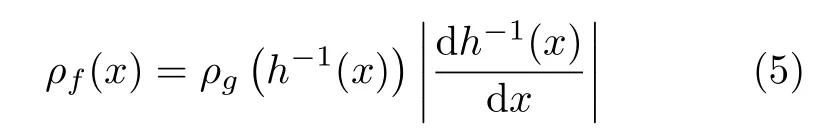
定理2对于一般3 次多项式f(x)=ax3+bx2+cx+d，若满足条件式(3)，则f的概率密度为

证明T3服 从[ 0,3/2]上的均匀分布，其概率密度为

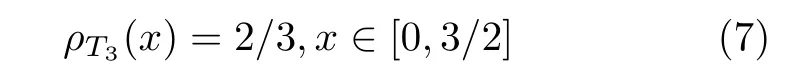
由定理1可知，f 和T3关 于h 拓扑共轭，且

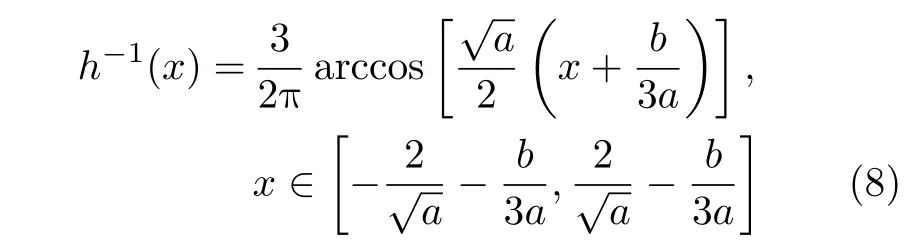
则根据引理2，f 的概率密度为

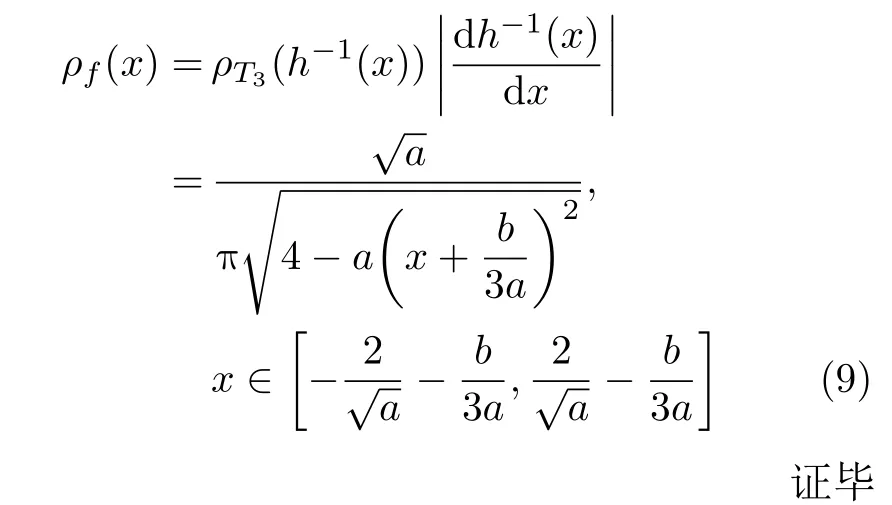
这类3次多项式混沌映射的概率密度函数的形式，是进一步将3次多项式混沌映射均匀化或基于3次多项式混沌映射产生独立同分布的混沌密钥流[11,12]的理论基础。

2.4 分岔图和Lyapunov指数

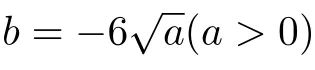
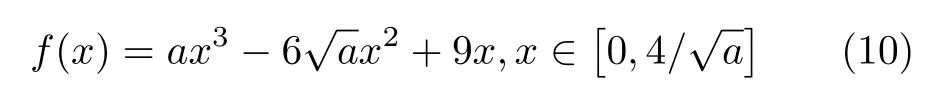
在系统(10)中，固定 a ∈[1,4]，系统的分岔图和Lyapunov指数谱见图2。

3 性能分析

本节对分段线性混沌映射 T3和3次多项式混沌映射f 的统计性质进行进一步的对比分析。

3.1 均匀性

信息熵是信息论中用于表征信源的不确定性程度。本文用信息熵度量混沌系统产生的混沌伪随机序列的不确定性程度。现在给出信息熵的定义。

定义2设 S ={x1,x2,···,xn}是一种信息源，P为S的一个概率分布，记xi的 概率为pi。则信源的信息熵定义为

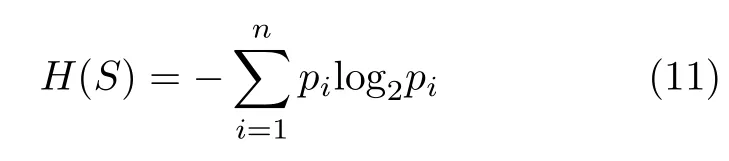
根据最大信息熵原理，当信源的概率分布为等概率分布，即pi=1/n时 ，信息熵能取得最大值l og2n。

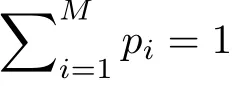
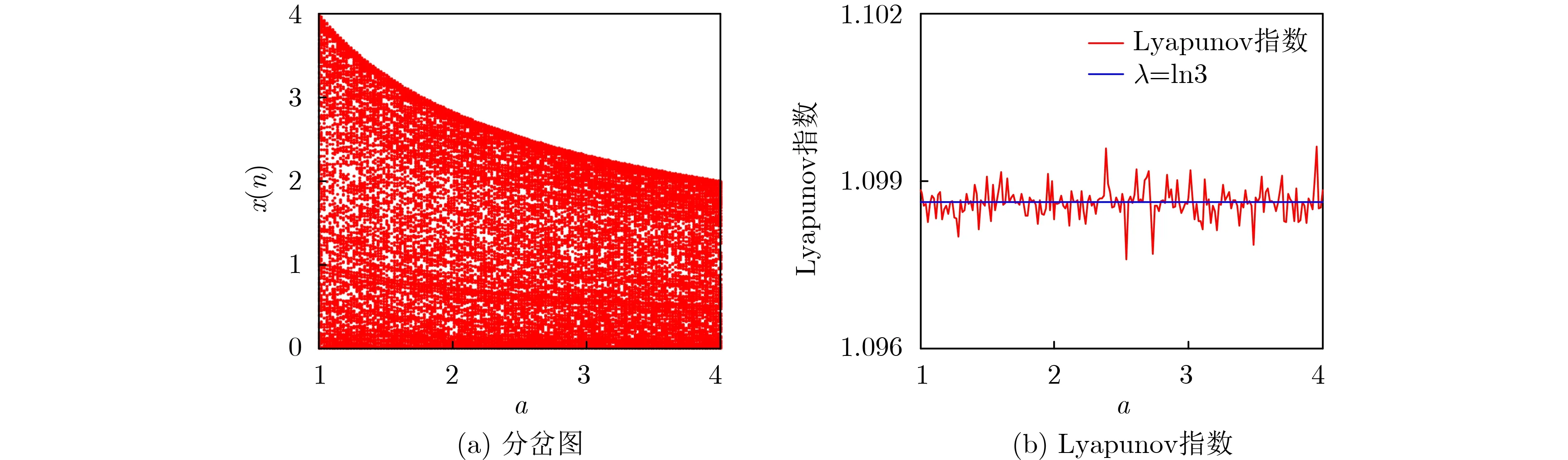
图2 系统(10)的分岔图和Lyapunov指数

下面选定N =106, M =28=256 ，以T3和系统式(10)为例，对拓扑共轭的这两类混沌系统进行信息熵分析，结果见图3。此处，序列的最大熵为8。

由图3可见，映射 T3的信息熵接近最大值8，从数值上验证了其均匀分布特性。其中， Pk为相对功率谱密度， N是混沌序列的长度，se是信号的谱熵，SE是se归一化后的谱熵，其最大值是1。

根据香农熵的性质，序列功率谱分布越均衡，则序列频谱结构越复杂，信号没有明显的振荡规律，得到的SE测度值越大，即复杂度越大。下文直接用SE的值度量伪随机序列的结构复杂度，简称为SE复杂度。

本文主要考察二进制伪随机序列的SE复杂度，并采用如下量化方法将生成的混沌序列{ z(n)}转换为二进制的混沌伪随机序列{ y(n)}：

(1) 给定混沌系统的参数和初值，并进行 n次迭代，得到混沌序列{ z(n)}；

3.2 结构复杂性

3.2.1 谱熵算法和量化方法

在文献[16]中，谱熵(Spectral Entropy，SE)算法被用于分析混沌伪随机序列的结构复杂度，并得到了谱熵算法的计算速度快、实时性好以及可准确分析混沌伪随机序列的复杂度等结论。本文采用谱熵算法对分别基于拓扑共轭的映射 T3和3次多项式混沌映射的混沌伪随机序列的结构复杂度进行研究。具体的谱熵算法见文献[16]，下面仅给出谱熵的计算公式

(2) 从序列 {z(n)} 截取长度为n0的随机序列{x(n)}，其中x (k)=z(k+1000)；

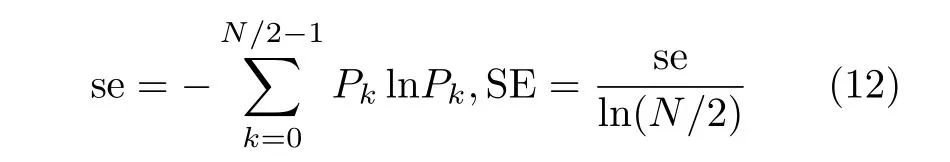
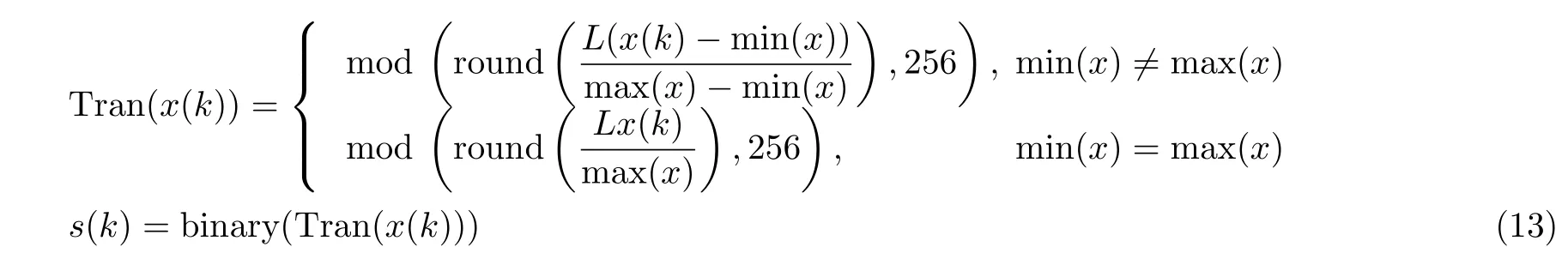
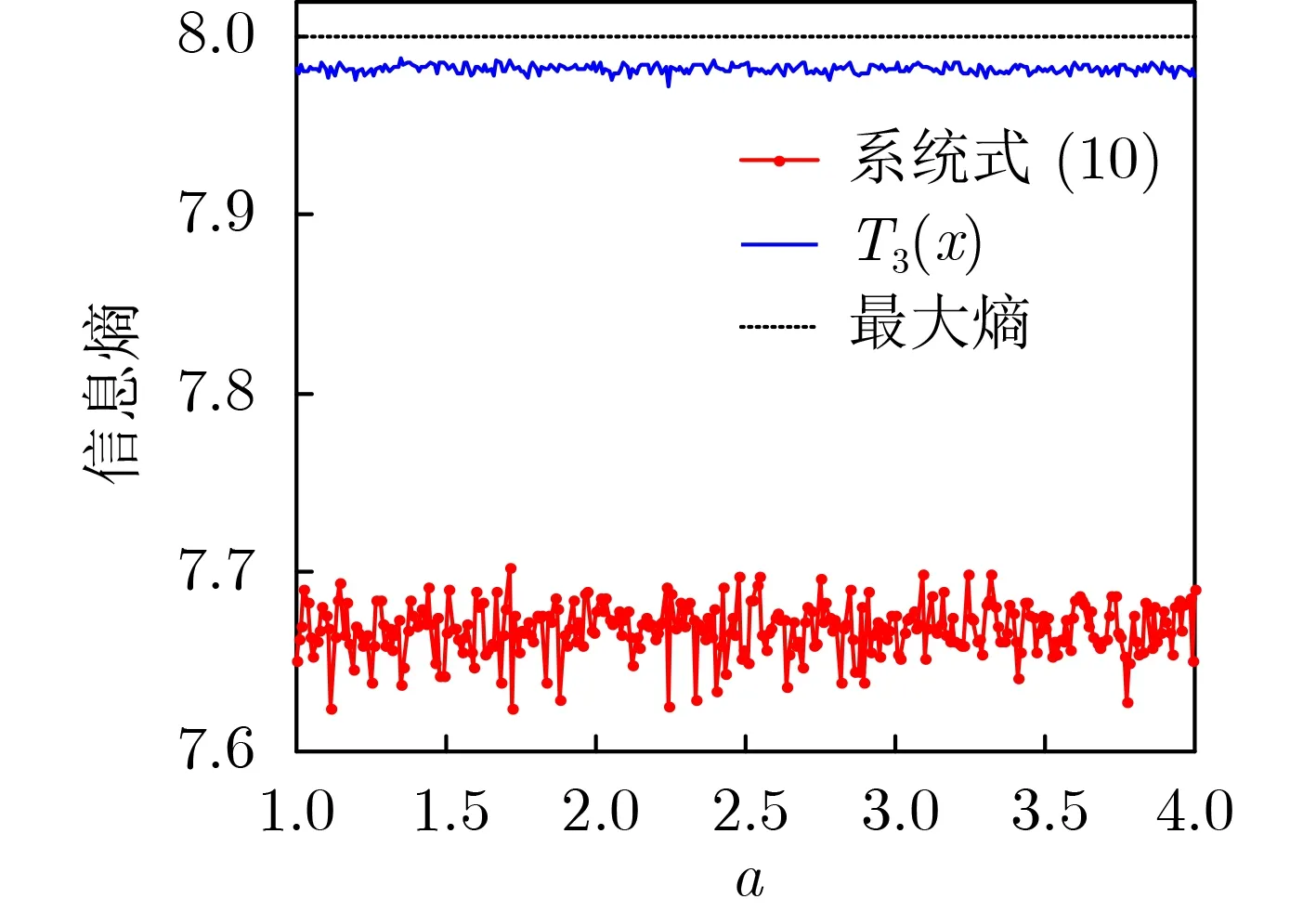
图3 映射T 3和系统式(10)的信息熵

在下文的SE复杂度分析中，若无特殊说明，则取序列长度N =1000。

3.2.2 SE复杂度分析

下面采用谱熵算法对映射 T3和系统式(10)产生的伪随机序列进行SE复杂度分析。

在系统式(10)中，取参数a =1， 迭代初值x0=1.2；两混沌系统的伪随机序列的SE复杂度随序列长度 N变化的曲线见图4(a)。在系统式(10)中，固定参数a ∈[1,4]，两混沌系统的伪随机序列的SE复杂度随参数a 变 化的曲线见图4(b)。图4(c)是当a ∈[2.004,2.124]时，两混沌系统的伪随机序列的SE复杂度随参数a 变化的曲线(图4(b)的局部放大)。

图4 不同系统的伪随机序列的SE复杂度

由图4可知，两者的SE复杂度不存在明显的差异。本文将混沌序列量化成二进制伪随机序列的量化方法(记为M1)和文献[16]中的量化方法(记为M2)不同，以下进一步分析不同量化方法对于SE复杂度的影响。

在保持其他条件相同的情况下，采用文献[16]的量化方法得到二进制伪随机序列，并进行SE复杂度分析，结果见图5。

由图5可见，在SE复杂度方面，量化方法对系统的结构复杂性影响显著，与文献[16]中的量化方法比较，本文的量化方法对应的系统的SE复杂度更高。

3.3 随机性分析

采用3.2.1节的量化方法，本节得到分别基于系统式(2)和系统式(10)的伪随机数发生器(Pseudo-Random Number Generator, PRNG)，并对比分析两系统的伪随机序列的随机性。

本节采用NIST提出的SP800-22检测标准[17]对混沌系统生成的二进制伪随机序列进行随机性检验。根据定理1，选取1000组不同的参数和初值，由PRNG生成1000组不同的二进制伪随机序列，并进行SP800-22随机性检测，结果见表1。

由表1可知，基于系统式(10)的PRNG通过了SP800-22随机性检验，而基于系统式(2)的PRNG不能全部通过SP800-22随机性检验。可见，拓扑共轭的两个混沌系统在使用本文的量化方法量化之后的随机性存在显著差异。3次多项式混沌映射与分段线性混沌映射T3相比更适合用于设计PRNG。

图5 不同量化方法下，不同系统的伪随机序列的SE复杂度

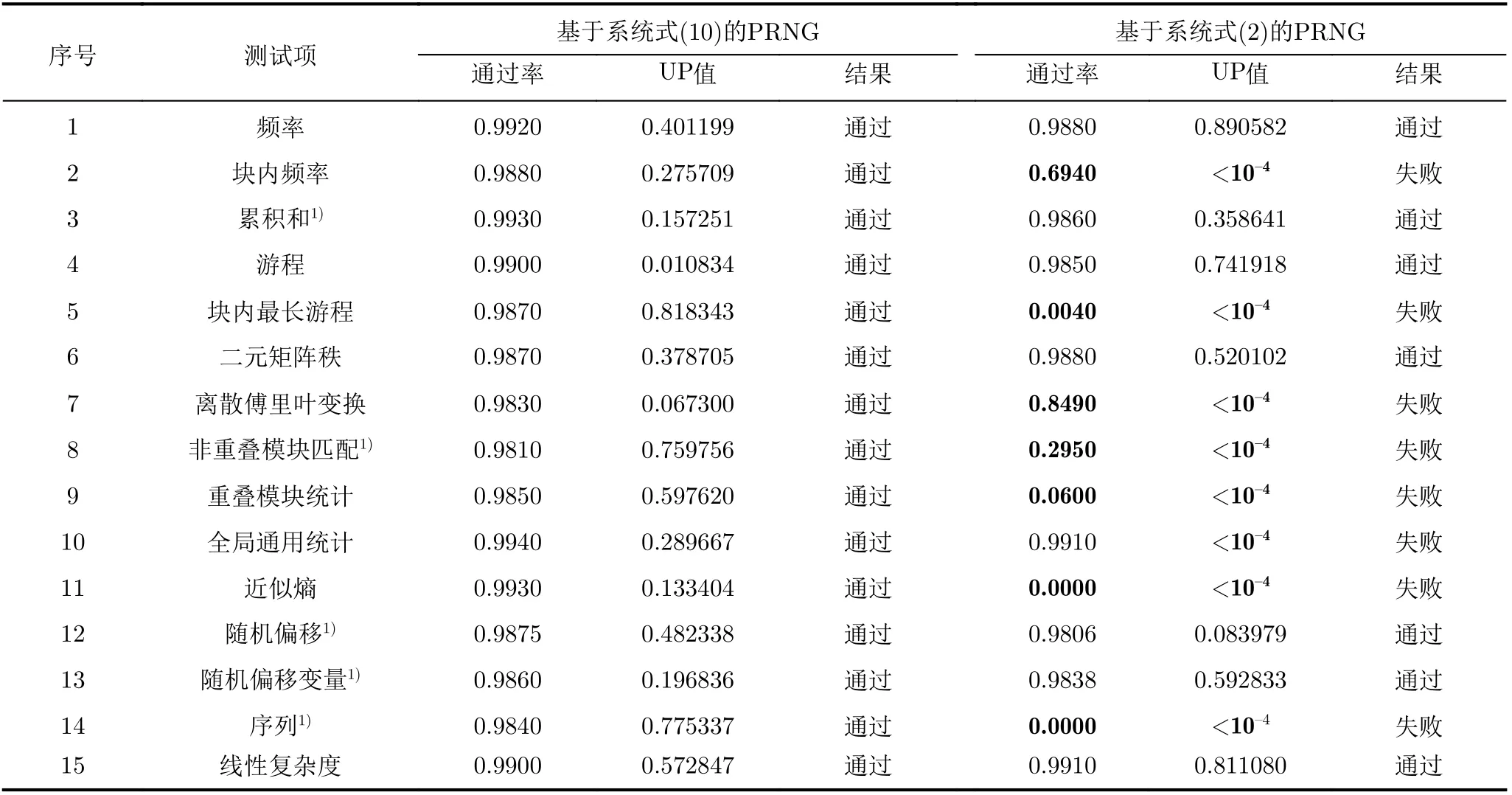
表1 NIST SP800-22检测结果

4 4次多项式混沌映射和 T4的拓扑共轭

用同样的思路和方法可以得到的表达式为

进一步可以得到，针对一般4次多项式f(x)=ax4+bx3+cx2+dx+e 和 映射T4，若满足条件

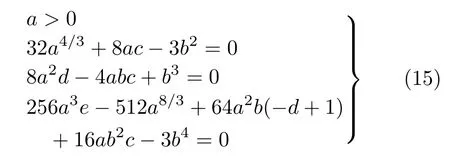
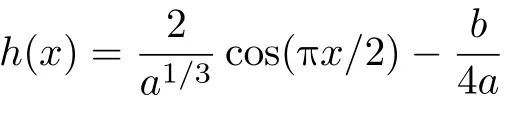
证明思路与定理1类似，证明过程略。

5 结论

本文基于一个分段线性混沌映射，分别给出了这个映射与3次多项式映射拓扑共轭的充分条件。从而间接地给出了一般3次多项式能成为混沌系统的充分条件。结合分段线性混沌映射的均匀分布特性，给出了这类3次多项式混沌映射的概率密度函数，这是进一步将3次多项式混沌映射均匀化或基于3次多项式混沌映射产生独立同分布的混沌密钥流的理论基础。对分段线性映射和多项式映射的均匀性、结构复杂性和随机性的分析结果显示，分段线性映射的均匀性优于多项式映射，而多项式映射的随机性优于分段线性映射，在结构复杂性方面，二者的结构复杂性并无显著差异，进一步给出了量化方法对二者的结构复杂性影响显著的结论。