一般常宽多边形的构造
段博韬
(淮北师范大学 数学科学学院,安徽 淮北235000)
0 引言
数学家对于常宽凸集的研究经历漫长且丰富的历史,并且在医学、机械工程、计算机、建筑、化工、地理等领域具有广泛应用[1-2]. 常宽凸集的概念由欧拉首次提出. 1876年,Reuleaux构造以正三角形三个顶点为圆心,以边长为半径的外接圆弧构成的非圆常宽曲线,后人称之为Reuleaux三角形. 该方法被推广在奇数边正多边形上得到Reuleaux正多边形[3]. 之后,Meissner将Reuleaux三角形推广至三维空间[4],构造出两种不同的三维常宽凸集. 1915年,Blaschke与Lebesgue分别证明平面上等宽度的常宽凸体中Reuleaux三角形面积最小,这个定理就是著名的Blaschke-Lebesgue定理[5]. 对于这个命题,国内外的数学家们又先后给出其他巧妙的证明[6-8]. 2007 年,Robert 等用数学归纳法给出一种n 维常宽凸集的构造方法[9].
平面上非圆常宽凸体的例子非常有限. 除比较经典的Reuleaux正多边形,潘生亮利用Minkowski支撑函数得到一类新的光滑的常宽凸集[10];Martini等利用Reuleaux三角形构造平面中新的常宽凸集[11];徐文学构造一类新的偶数边常宽凸集[12].
在这些经典构造的基础上,本文首先使用多次旋转固定长度的线段的作图方法构造一类圆弧构成的平面图形;其次证明这类图形在闭合条件下具有常宽性质;最后,利用线性规划约束条件的基本可行点[13],求出闭合条件下的全体可行点,并以此推广Reuleaux多边形的构造方法.
1 预备知识
记Rn为带有标准内积的n维欧氏空间,Sn-1为Rn中的单位球面. 点集K ⊂Rn称为凸的,如果对任意x,y ∈K, 连接x,y 的线段[x,y]完全包含于K 内[14]. 若K 为内部非空的紧致凸集,u ∈Sn-1,则称

为K 在u 方向上的支撑超平面[15]. 当K 的任意一对平行的支撑超平面H(K,u),H(K,u),u ∈Sn-1间的距离恒为常数d(d >0)时,称K 为宽度为d 的常宽凸体. 平面上常宽凸体的边界称为常宽曲线,圆是典型的常宽曲线.
2 主要结果
通过对经典Reuleaux多边形的归纳,下面给出一类平面图形的作图方法.
作法作平面上一个长度为d(d >0)的线段A0B0(如图1所示).

图1 多次旋转固定长度的线段

图2 曲线α 在不同方向上的杠杆相交
(a)令i=1,2,…, n,点Oi为线段Ai-1Bi-1上一点(可以取Ai-1,Bi-1),点Ai-1,Oi之间距离为ri(0 ≤ri≤d).以Oi为旋转点逆(顺)时针旋转线段Ai-1Bi-1,旋转角度后得到线段AiBi及圆弧(允许圆弧半径ri或d-ri为0,即对应圆弧退化为点).
(b)令点On+1为线段AnBn上一点(可以取An,Bn),点An,On+1之间距离为rn+1(0 ≤rn+1≤d),以On+1为旋转点逆(顺)时针旋转线段An,Bn,旋转角度后得到线段An+1Bn+1及圆弧(允许圆弧半径rn+1或d-rn+1为0,即圆弧退化为点).
注1在上述作图中,设点A,B 分别在圆弧上,且线段AB 过旋转点Oi,其中i=1,2,…, n, n+1 .若=du,u ∈S1,则称线段AB 为该图形在方向u 上的杠杆,旋转点Oi为杠杆AB 的支点.
注2在上述作图中,若圆弧组成的曲线闭合(即点An+1与点B0重合,点Bn+1与点A0重合),且各方向上的杠杆长度恒为d(d >0),记L(d)为这类闭合曲线的全体.
于是,可以证明如下结论.
定理1若α ∈L(d),d >0,则α 为平面常宽曲线.
证明对∀u ∈S1, 存在α 在方向u 上的一条杠杆[x0,y0],其中x0=y0+du,x0,y0∈α.令u=(0,1),由α 的封闭性,可以将杠杆[x0,y0] 沿曲线α 依照上述作图方法逆时针旋转φ(φ ∈[0,π]) ,得到α 在方向u(φ)=(cos φ,sin φ) 上 的 杠 杆[ ]x(φ),y(φ) , 其 中x(φ)=y(φ)+du(φ), x(φ),y(φ)∈α. 进 而 可 以 将x(φ) 表 示 为,其中ri∈[0,d],0=φ1<φ2<…<φs=φ.由sin φ ≥0,φ ∈[0,π]容易得到. 同样地,将杠杆[x0,y0],沿曲线α 依照上述作图方法顺时针旋转φ(φ ∈[0,π]),得到α在方向u(-φ)上的杠杆[x(-φ),y(-φ)] ,可得
仿照上述的讨论,结合y0=x0-du,y(φ)=x(φ)-du(φ),同理可得
综上,曲线α 在u 方向上的宽度为d.又由u 的任意性可知,封闭曲线α 在任意方向上的宽度恒为d,曲线α 是宽度为d 的常宽曲线.
定理2若α ∈L(d),d >0, 则对任意u1,u2∈S1, u1≠±u2,α 在方向u1,u2上的杠杆必存在唯一交点.
证明如图2 所示,令线段[x1,y1], [x2,y2]分别为曲线α 在方向u1,u2上的杠杆,其中x1=y1+du1,x2=y2+du2,x1,x2,y1,y2∈α.由定理1的证明过程可知

因u1≠±u2,故支撑线H(α,u1),H(α,-u1)与支撑线H(α,u2),H(α,-u2)不平行. 进而曲线α 包含于支撑线H(α,u1),H(α,-u1),H(α,u2),H(α,-u2)构成的平行四边形区域中,点x1,y1与点x2,y2分别位于平行四边形两组平行的对边上. 显然,线段[x1,y1]与[x2,y2]有唯一交点.
下面讨论由上述作图方法所得曲线的闭合条件. 由定理2可知,对任意i=1,2,…,n, 上述过程中的杠杆AiBi与杠杆A0B0有唯一交点,设交点为Pi,线段B0Pi长度为si,线段AiPi长度为ti, 其中si,ti∈[0,d],i=1,2,…,n.显然,曲线闭合当且仅当sn=tn.此时,点Pn为杠杆AnBn,An+1Bn+1上的支点On+1,并且圆弧的半径

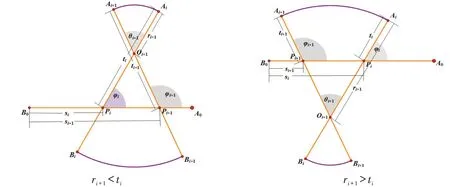
图3 两种情形下数列{si},{ti}的递推关系

其中t1=r1,s1=d-r1,i=1,2,…,n-1.由式(2)整理得sin φi+1ti+1-sin φiti=ri+1(sin φi+1-sin φi).两边求和得到数列{sin φmtm},m=2,3,…,n 的通项公式

于是,数列{tm} 的通项公式


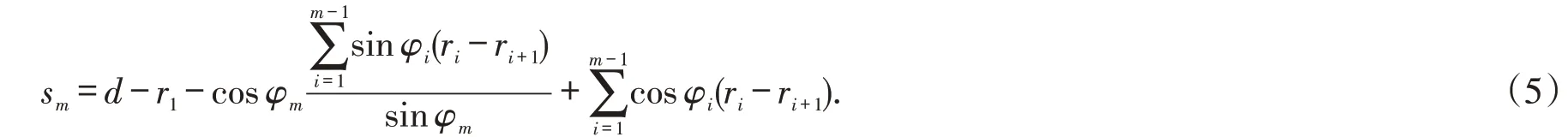
若曲线闭合,当m=n,将式(1)代入式(4)和式(5),得

结合式(6),可以将曲线闭合的约束条件整理为

注意到,圆能够由上述作图方法得到,故任意取φ1,φ2,…,φn满足0 <φ1<φ2<…<φn<π,则r1=r2=…=rn+1=是式(7)的一个解. 因此可以任意取φ1,φ2,…,φn(0 <φ1<φ2<…<φn<π)为某些固定值,结合变量r1,r2,…,rn+1的有界性,将曲线的闭合条件表示为线性规划问题的单纯形可行域.
令rm=xm,将式(7)转化为线性规划约束条件的标准形式,可得

其中:松弛变量xn+m+1为圆弧的半径d-rm,m=1,2,…,n+1 .
由于单纯形为凸多胞体,因此利用式(8)的基本可行解(即单纯形可行域的顶点)的凸组合可以表示出满足闭合条件的解集. 下面应用这种方法构造具体的常宽多边形.
例1当n=3,d=1时,取φ1=0.3,φ2=1.7,φ3=2.4,代入式(7)得到闭合条件
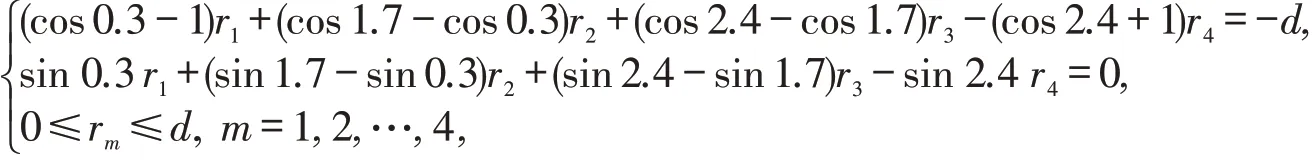
共解得6个基本可行解X1,X2,…,X6(精确到0.000 1).

应用本文作图方法可以分别作出这些基本可行解对应的常宽多边形(如图4).

图4 基本可行解对应的常宽多边形
例2当n=4,d=1时,取,代入式(7)得到闭合条件

共解得12个基本可行解X1,X2,…,X12(精确到0.000 1).

任取基本可行解的凸组合

应用本文作图方法可以作出可行解X对应的常宽多边形(如图5).

图5 可行解X 对应的常宽多边形

