基于二步二阶边界值法的电磁暂态并行算法

李博文，张 磊，叶宇国，张 静

（1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.国网湖北省电力公司枣阳供电公司，湖北 枣阳 441200）

随着电力系统的规模越来越大以及越来越多的电力电子设备应用于电力系统中，电网的动态特性变得越来越复杂，对于电力系统仿真实时性的要求也变得越来越高［1-2］。目前已有许多商业化的电磁暂态仿真软件。其中，基于EMTP类算法的电磁暂态程序目前已经成为设计电力设备和电力系统的一个必备工具，在技术研究和程序开发中也扮演着越来越重要的角色。Power System Toolbox，PSCAD/EMTDC，Transient Performance Advisor（TPA），EPRI/DCG等众多仿真软件都是基于EMTP所开发［3］。

电磁暂态数值计算所采用的时间尺度往往非常小，通常是微秒级［4］。对于特快速暂态过电压（very fast transient overvoltage，VFTO）的计算，所采用的积分步长会更小，一般是纳秒级［5］。因此即使仿真时间很短，其对应的计算量依旧很大，这是造成现有电磁暂态仿真程序实时性不足的原因之一。同时现有的大多数商业电磁暂态仿真软件，往往是基于传统的串行计算模式，因此不可避免的面临计算效率低的问题，这也是造成仿真实时性不足的原因之一。

为了满足对电力系统仿真实时性的需求，就必须提高电磁暂态数值计算的计算速度，对此有2个途径，一个是采用新的数值算法［6-7］，另外一个是并行计算技术。其中并行计算技术可以通过2种手段实现：一是空间并行，考虑通过长输电线将电力系统分割得到完全解耦的子系统，各子系统可以独立并行计算［8-9］。但是由于各个子系统的时间常数不同，若根据时间常数最小的子系统确定积分步长，则会严重浪费计算资源，增加仿真时间，为了解决这个问题，文献［10］结合多速率电磁暂态仿真技术，根据不同的子系统确定不同的积分步长，优化了计算资源，提高了电磁暂态仿真效率。二是时间并行，考虑将数值算法并行化，文献［11］在临界阻尼调整法的基础上，利用矩阵对角化技术，可实现精确的时间解耦并行计算。文献［12］基于不动点迭代，推导出了一套收敛性更好的电磁暂态时间并行算法。

本文从并行化数值算法的角度出发，基于二步二阶边界值方法，对一阶常微分方程进行离散，通过牛顿法对离散后的方程进行求解。离散后的雅克比矩阵是块三对角矩阵，对于这种形式的矩阵，常用的方法是追赶法［13］，追赶法是一种快速的串行方法，本质是高斯消元，无法实现并行化。本文将初始雅克比矩阵重新排列为等价矩阵，通过一个耦合矩阵，将大矩阵分解为各自独立的小矩阵，推导出了二步二阶边界值并行算法（boundary value parallel methods，BVPM）。为了验证本文算法性能，最后通过2个典型的非线性电磁暂态算例进行数值测试，将本文算法与追赶法和EMTP类方法进行比较。

1 二步二阶边界值法简介

边界值方法是L.Brugnano等学者为了克服传统线性多步法存在的稳定性以及阶障碍所提出的一大类方法。按照L.Brugnano的思路，边界值方法主要分为3类［14］：广义向后差分法、广义Adams以及拓展的梯形积分公式。这3类方法均突破了Dahlquist限制性定理，它们都是A-稳定的数值方法。因此在数值稳定性方面均要优于传统的线性多步法。除此之外，L.Lopez还提出了一种特殊的二步边界方法，并研究了其稳定性和收敛精度［15］。

考虑一阶常微分方程初值问题为：

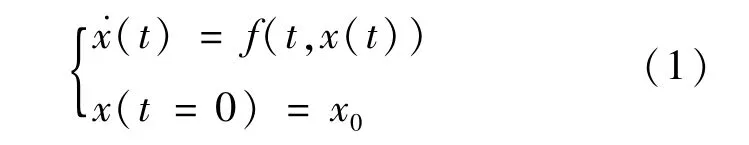
式中：t表示时间；f（t，x（t））表示时间t和变量x的函数；x0表示变量x在t=0时的初始值。

本文采用带独立参数的二步二阶边界值方法离散式为：

式中：h=tn+1-tn=T／N，T表示仿真时长，N表示时间离散网格点数。

文献［15］已经证明，当θ＜-1时，具有（1，1）边界条件的二步二阶边界值方法是一种A-稳定的数值方法，稳定域如图1所示。图1中边界曲线外部为二步二阶边界值法的稳定域。

图1 二步二阶边界值法稳定域示意图

显然，对于微分初值问题，通常只有x0是已知的，而xN是未知的，因此还需要添加一个附加方程作为边界条件，本文选用隐式梯形法为时域末端的附加方程，即：

2 基于二步二阶边界值的并行算法

2.1 并行实现

利用二步二阶BVM法作为主方法，隐式梯形积分方法作为附加方法对式（1）进行连续的时域差分离散，然后再利用牛顿法对离散后的方程进行整体求解，得到的雅克比矩阵方程为：

式中：J为整体雅克比矩阵：▽F表示牛顿残差向量。

式中，Im为m维单位矩阵。

通过式（6）可以看出，由于二步二阶BVM是对整个积分区间一次性求解出所有时间节点上的点，从而导致式（5）的维数会非常大，存在“维数灾”问题。

为了解决这一问题，常采用直接或迭代的方法求解。具体的，对于式（5）形式的分块三对角矩阵，往往采用追赶法进行求解［13］，但是追赶法本质上是一种串行方法。本文针对式（5）的结构特性，通过交换行块和列块，对雅克比矩阵进行重排，重排后的方程记为：

式中：u=［Δx1，Δx2，Δx4，Δx5，…，ΔxN］T；v=［Δx3，Δx6，Δx9，…，ΔxN-2］T；

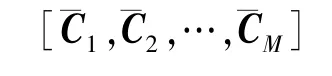
D=diag［P3，P6，…，PN-2］。A，B，C，D矩阵中，M为子系统数。

初始矩阵被简化为一些新的对角独立块矩阵、2个辅助块矩阵以及1个耦合块矩阵。根据式（7），可以得到：

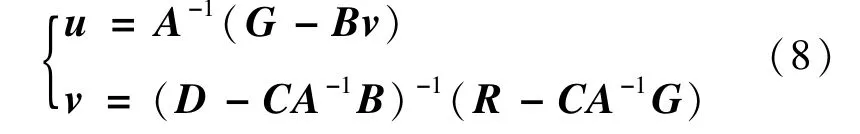
为了避免对矩阵A求逆，于是令：

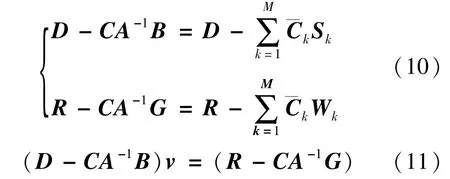
基于上述推导，将二步二阶BVM并行算法概述如下：

1）根据需要确定需要离散的时间点个数N以及时间积分步长h。

2）利用二步二阶边界值方法作为主方法，隐式梯形法作为时域末端附加方法，对微分方程进行离散。

3）利用牛顿法对离散后的方程整体求解，确定雅克比矩阵，将大系统雅克比矩阵分解为M组独立的小系统矩阵，由矩阵D耦合到大系统中。

4）根据式（11）计算出矩阵v，再根据式（12）并行计算出矩阵u。

5）收敛性判断，若收敛，则计算结束，若不收敛，则转到新一轮牛顿迭代中，直至收敛。

显然，本文算法需要用到三角分解的有式（9）和式（11），但是由于该方法的并行结构以及新块矩阵的维数远远小于原矩阵的维数，因此本文算法理论上会比直接利用追赶法求解式（4）方法具有更高的计算效率。

2.2 加速比分析

为了评价本文算法的加速效果，将本文算法与追赶法的计算速度进行对比分析。定义加速比为：

式中：λ表示加速比；tBVM、tBVPM分别表示追赶法和本文所提并行算法的计算时间。

通过考虑块矩阵的矩阵运算次数来估计算法的计算速度。由于矩阵的加法运算所消耗的时间远比乘法运算小，因此忽略加法运算，只考虑乘法运算。根据文献［16］，假设n×n的块矩阵做一次矩阵乘法和求逆运算均需要n3次乘法运算。

追赶法本质还是高斯消元法，利用雅克比带状稀疏矩阵的非零系数分布特点，来提高运算速度，但它是一种串行方法，不具备并行化特点。追赶法求解式（4）所需要的矩阵运算次数为：

对于本文算法，使分解后的每一个子系统有着相同的大小，保证每一个计算单元的计算量大致相同，避免了因为等待某些计算量大的计算单元而延长求解时间。设Nk表示子矩阵的对角块数（k∈［1，M］），并且有：

得到二步二阶BVM并行算法的块矩阵运算次数为：

假设参与并行计算的计算单元的数量为P，各个子系统大小相等，且子系统数M=iP，每个计算单元都按照各自所对应子系统队列，顺序执行操作。我们可以得到加速比的近似值为：

图2给出了在不同i值情况下，并行度（计算单元数量P）与理论加速比λ关系的曲线。

图2 理论加速比

通过图2可以发现，当计算单元数量较小时，加速比与计算单元数量呈近似线性增长的关系，随着计算单元的增加，本文算法非并行的部分会逐渐增大，加速比的增长速度会慢慢变缓，理论加速比会在达到最大值后开始降低。同时我们可以发现，随着i值的增加，加速比的最大值变得越来越小。当计算单元较少时，i值对于加速比的影响并不大，然而随着计算单元的增加，i值越大，本文算法非并行计算部分增加得就越快，导致加速比的最大值急剧下降。因此，为了充分发挥本文算法的性能，除了要满足各子系统大小要相同，还必须要满足子系统数M等于计算单元的数量。计算单元数量通过图2所示所能达到的最大加速比时的并行度来确定。

3 算例分析

3.1 算例1含非线性负荷的高压输电线路

图3为一个含非线性负荷的高压输电线路示意图。其中es（t）为激励电压源，开关在t=0 s时合闸。输电线路送端内电阻Rs=20Ω、内电感Ls=0.06H。输电线路受端的非线性负荷是由非线性电感和负荷电阻并联组成。负荷电阻RL=96Ω，非线性电感的磁链φ与线路电流iL满足φ=a tanh biL，其中a=8.4×10-2，b=5.95×10-3。

描述输电线路的电磁暂态仿真过程，一般采用著名的电报方程。电报方程是一种双曲偏微分方程，因此需要将其转换为式（1）的常微分方程。考虑到高压输电线路可以忽略电导，因此本文采用π型级联的等效电路对输电线路进行建模［17］。

图3 含非线性负荷高压输电线路

输电线路分为30段，根据基尔霍夫电压、电流定律，可以列写出上述空间离散的π型等效电路的电路方程为：

式中，l、c、r分别表示离散后的每一段线路的电感、电容以及电阻。其值依次为：

当开关闭合时，应该满足如下边界条件：

为了验证本文算法的计算性能，将本文算法与经典的EMTP算法的计算结果进行了对比。本文算法独立参数θ=-2，时间积分步长均取h=10-6s，牛顿迭代的收敛精度设置为ε=10-4。图4和图5分别为2种方法计算的送端、受端电压曲线。从图4、图5中可以看出，在相同的积分步长情况下，本文算法有着与EMTP类方法相当的计算精度。在一些变化波动较为剧烈的地方，本文算法也能与EMTP类方法的结果基本吻合。本文算法只需要迭代2次即可达到收敛精度要求，与EMTP类方法的迭代次数相同，显然本文算法具有良好的收敛性。

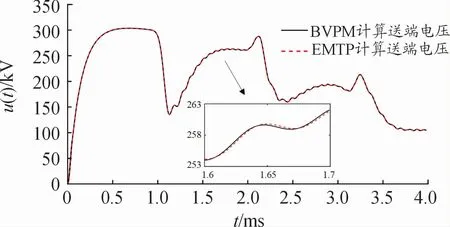
图4 送端电压

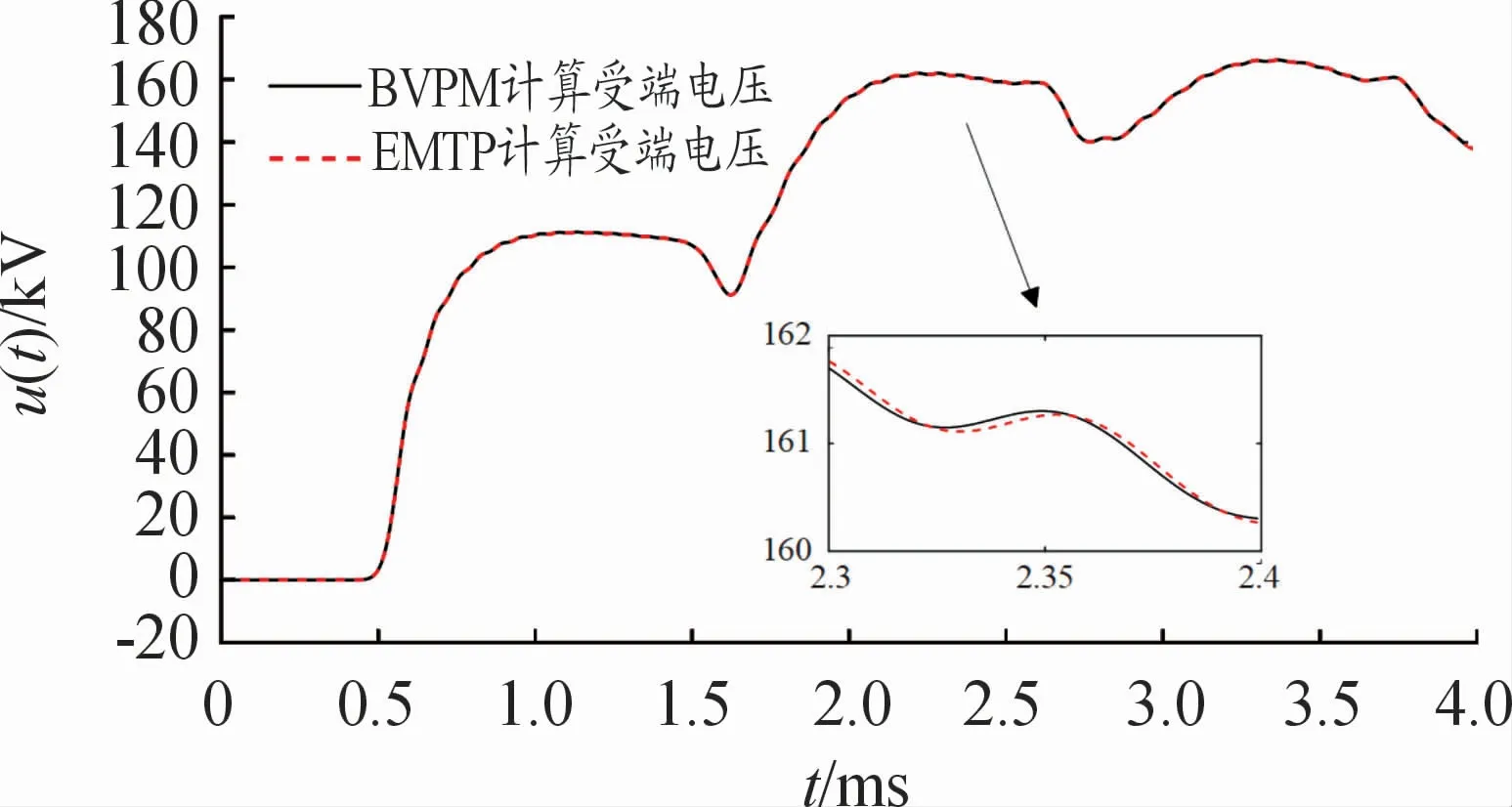
图5 受端电压

在时间积分步长相同的情况下，将EMTP类方法与本文算法的计算时间比值定义为加速比λ1，追赶法与本文算法的计算时间比值定义为加速比λ2。在不同的并行度下，本文算法的计算时间与加速比如表1所示。

表1 算例1 BVPM计算时间及加速比

从表1可以看出，在并行度等于2时，BVPM的计算效率低于EMTP类方法，这是由于BVPM算法是对整个积分区间一次性求解出所有时间节点上的值，所得到的矩阵维数高，在低并行度下，计算机处理起来花费的时间依旧比EMTP类方法更多，但是随着并行度的增加，BVPM的加速效果逐渐体现出来，计算时间明显小于EMTP类算法。

3.2 算例2 VFTO 含非线性负荷的高压输电线路

随着超高压和特高压输电技术的不断发展，气体绝缘开关设备（gas insulated switchgear，GIS）被广泛运用。当GIS设备中隔离开关投切空载短母线时，开关触头间隙会被多次重复击穿，从而在GIS设备中产生VFTO。因为VFTO具有频率高、幅值大、陡度高等特点，所以会对电力系统一次设备和二次设备带来一定的危害。因此关于VFTO的建模、数值计算等是研究特高压电力系统电磁暂态的重要内容。图6是一个550kV GIS中的VFTO计算的简化模型。其中，L1和L2表示连接的短母线，用无损的短传输线模拟，单位长度的电感L0=2.5×10-7H/m、电容C0=4.45×10-11F/m；LT和CT分别表示变压器的等值电感和对地电容。DS表示隔离开关，CR表示隔离开关的对地电容。隔离开关合闸过程的电弧模型用一个非线性时变电阻来表示为：

式中：τ1=1 ns；τ2=1μs。

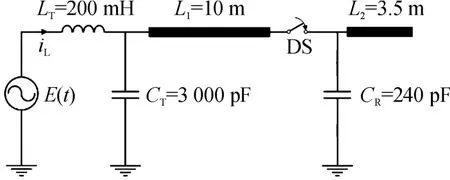
图6 VFTO计算简化模型示意图

采用π型等值电路等值短母线，短母线L1和L2分别均分为20段和7段，则可以将VFTO的计算用式（1）微分方程表示。

利用本文算法和EMTP方法对VFTO计算模型进行仿真，牛顿迭代的收敛精度设置为ε=10-4，时间积分步长均取h=0.1 ns。当电源侧电压与短母线残余电压之差达到2.0 p.u.时，VFTO所产生影响最为严重，因此将电源侧电压设置为1.0 p.u.，短母线负荷侧电压设置为-1.0 p.u.。

图7为本文算法计算出的L2线路末端电压，其中差值曲线是本文算法与EMTP方法比较的结果。从图7中可以看出，本文算法与EMTP方法计算结果差别不大，有着相同的计算精度。

图7 VFTO计算结果

表2为本文算法计算时间以及与EMTP方法和追赶法的加速比结果。

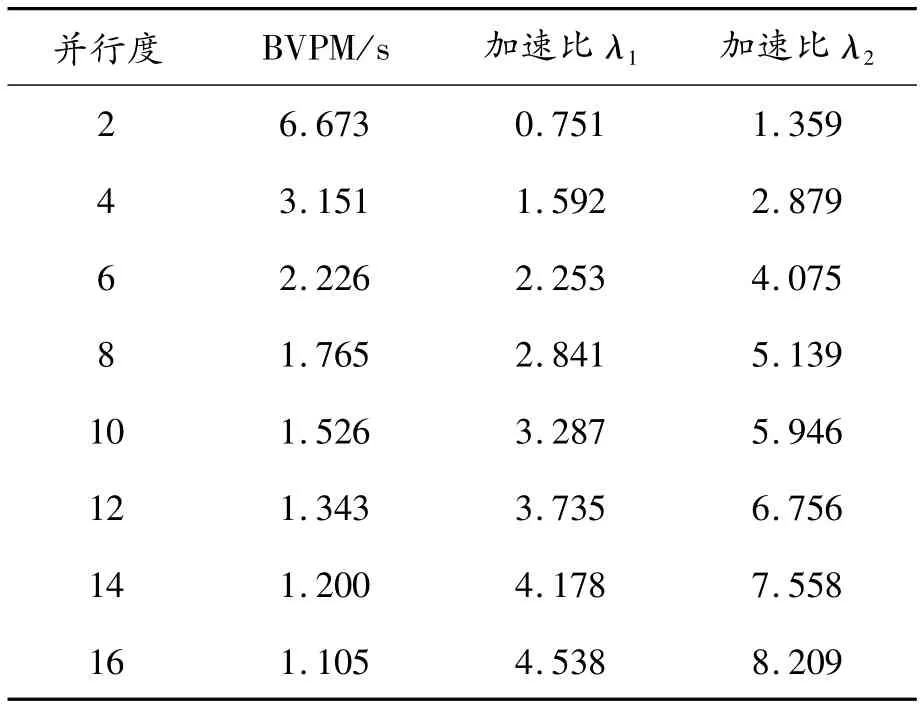
表2 算例2 BVPM计算时间及加速比

从表1和表2可以看出，本文算法的加速效果与理论分析结果相比稍差。究其原因，一方面是理论分析只考虑了块矩阵乘法运算的时间，忽略了加法运算的时间以及生成雅克比矩阵的时间；另一方面是理论分析时并未考虑内存管理时间。正是这2个原因导致实际的加速效果与理论分析结果之间的差异。但总的来说，本文算法显著提高了电磁暂态仿真的计算效率。

4 结论

本文将二步二阶边界值法应用于电磁暂态数值计算，根据离散后的雅克比矩阵是块三对角矩阵这一特点，通过一个耦合矩阵，将初始矩阵分解为独立的子矩阵，提出了基于二步二阶边界值法的电磁暂态并行算法。

理论分析了本文算法和追赶法的矩阵计算成本，估计了其加速比。算例结果表明，本文算法收敛性好，有着与EMTP类方法相当的计算精度。计算效率高于传统的追赶法和EMTP类方法，有着良好的加速效果，能够极大减少电磁暂态仿真的计算时间。