二次四元数系统正定解的迭代法
黄敬频,张姗姗,熊昊
(广西民族大学数学与物理学院,广西南宁530006)
1.引言
本文研究二次四元数系统

的正定解,其中B ∈Qn×n,A,P >0(正定)是已知四元数矩阵,X ∈Qn×n是未知矩阵.
形如AY A∗−Y=P的矩阵方程称为离散型Lyapunov方程,它在系统控制及稳定性分析等方面有重要作用[1],多年来关于这类方程的对称解、正定解、极秩解和其他结构解有较多的研究成果[2−9].当Y,P作为已知矩阵求矩阵A就是这个方程的一类反问题.可见矩阵方程(1.1)正是离散型Lyapunov方程正定解反问题的推广形式,它是一个二次系统.目前关于二次矩阵方程的研究是热点课题.例如,文[10]在A=I,B是对角阵,P是非奇异M矩阵时讨论了一类二次矩阵方程(1.1)解的性质;文[11-13]在实数域上分别研究了如下二次矩阵方程XTDX+AX+XTB+C= 0,AXA=XAX,A0+A1X+A2X2=X的求解方法.2015年文[14]在四元数体上给出了方程AXA∗−X=F的酉矩阵约束反问题解.然而,在四元数体上关于方程(1.1)的正定解的迭代方法未见相关研究报导.
本文目的是讨论二次四元数系统(1.1)的自共轭正定解存在性及其迭代求解算法.用¯A,A∗分别表示四元数矩阵A的共轭和共轭转置,如果A∗=A,则称A是自共轭矩阵,全体n阶自共轭矩阵记作SCn(Q).符号λmax(A),λmin(A)分别表示自共轭矩阵A的最大和最小特征值.对于正定矩阵A,B,用A >B表示A −B是正定的.||A||= [tr(A∗A)]1/2表示四元数矩阵A的Frobenius范数.设A=A1+A2j∈Qn×n(A1,A2∈Cn×n),则称是A的复表示矩阵.关于算子Aσ的性质[15],这里从略.
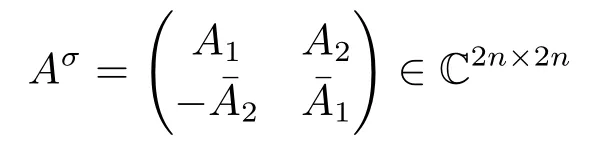
2.正定解存在条件及迭代方法

显然(1.1)存在正定解等价于(2.1)存在正定解.下面讨论(2.1)存在正定解的条件
引理1设M ∈SCn(Q),则二次四元数系统(2.1)存在自共轭正定解的充要条件是MQ=QM.
证如果(2.1)存在自共轭正定解Y,则Y2−Q=MY,两边取共轭转置可得

于是MQ=M(Y2−MY)=(Y2−MY)M=QM.反之,如果MQ=QM,则M,Q可同时酉对角化,即存在四元数酉矩阵U ∈Un×n,使得

其中

令Z=U∗Y U,则方程(2.1)等价于

取Z=diag(z1,z2,··· ,zn),则方程(2.3)有正定解Z >0等价于下列n个代数方程均有正实根

显然(2.4)中每个方程总存在唯一正根从而(2.1)存在自共轭正定解.证毕.
下面针对四元数矩阵M ∈SCn(Q)分别为正定、负定、不定三种情况,讨论方程(2.1)的正定解的迭代构造及其收敛性问题.
(I)讨论M ∈SCn(Q)为正定矩阵的情况.
引理2设M,Q >0,r1=λmax(M),rn=λmin(M),p1=λmax(Q),pn=λmin(Q),则方程(2.4)中i=1,n对应的两个方程的正根α,β满足β ≤α.
证由r1≥rn >0,p1≥pn >0立即可知α.证毕.
现考虑矩阵方程

其中M,Q ∈Qn×n是正定矩阵且MQ=QM.
引理3方程(2.1)与(2.5)具有相同的与M可交换的正定解.
证若Y是(2.1)的正定解,则由引理1的证明过程知Y M=MY,因此M,Y能同时酉对角化,即存在酉矩阵V ∈Un×n,使得M=V DMV∗,Y=V DY V∗,于是
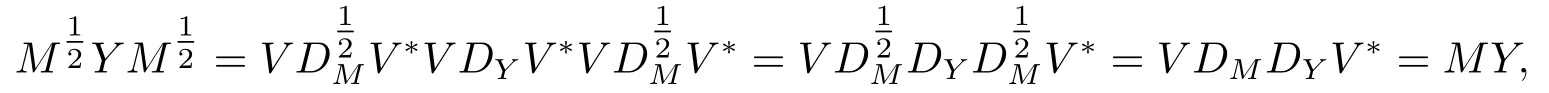
即Y也是(2.5)的与M可交换的正定解.反之,若Y是(2.5)且与M可交换的正定解,则由=MY可知Y也是(2.1)的正定解.证毕.
引理4设α,β是引理2给出的正数,则矩阵方程(2.5)在Φ=[βI,αI]内必存在正定解.
证建立矩阵函数

则由r1=λmax(M),rn=λmin(M),p1=λmax(Q),pn=λmin(Q),∀Y ∈Φ,有

且

因此,f(Φ)⊂Φ.根据Brouwer不动点定理,Y=f(Y)在[βI,αI]内存在不动点,即方程(2.5)在Φ内必存在正定解.证毕.
利用函数(2.6)构造迭代格式

定理1设M,Q ∈Qn×n是正定矩阵且MQ=QM,α,β是引理2给出的两个正数,则∀Y0=sI ∈Φ,β ≤s ≤α,迭代(2.7)总收敛到(2.1)的正定解.
证由引理1的证明过程可知,M,Q具有分解式(2.2),令Z=U∗Y U代入(2.5)可得相应的迭代格式
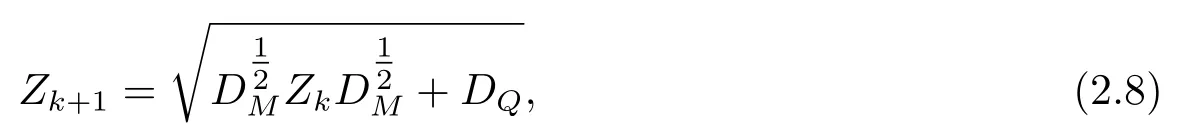
于是(2.7)收敛等价于(2.8)收敛.当Y0=sI(β ≤s ≤α)时,Z0=sI,这时

下面证明对每一个i由(2.9)确定的数列收敛.根据引理1,可设f(z)=z2−riz −pi=0的唯一正根为si.x若s ≤si,则有即有上界.同时由二次曲线性质可知f(s)=s2−ris −pi ≤0,因此有即{z(i)k }单调增,因此)}收敛.y若s >si,则有即有下界.同时有f(s)=s2−ris −pi >0,因此有,即单调减,因此收敛.从而(2.8)收敛到(2.1)的正定解.证毕.
根据定理1的证明过程,可得方程(2.1)的自共轭正定解表达式.
推论1设M,Q ∈Qn×n是正定矩阵且MQ=QM,则矩阵

是方程(2.1)的正定解,其中U由分解式(2.2)所给出,si是数列(2.9)的收敛点.
证因为si是数列(2.9)的收敛点,所以s2i −risi −pi= 0(i= 1,2,··· ,n).把矩阵(2.10)代入方程(2.1)左边得
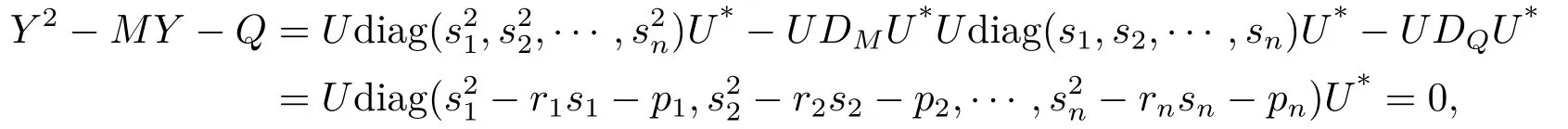
即(2.10)是(2.1)的正定解.证毕.
注1根据前面的讨论可知,由定理1或推论1求出的正定解满足不等式βI ≤≤αI,其中α,β是引理2给出的正数.
注2当矩阵阶数n较大时,对矩阵M,Q同时酉对角化较为困难,因此一般不用推论1中的公式(2.10)来计算方程(2.1)的正定解.此时采用迭代公式(2.7)只须估计α或β的近似值,就可选取初值矩阵X0=αI或βI,大大降低了计算复杂度.实际上根据引理2知

(II)讨论M ∈SCn(Q)为负定矩阵的情况.首先指出,当M <0,Q >0时,引理2的结论仍然成立.事实上,这时有

由方程(2.4)可知,z2−r1z −p1= 0与z2−rnz −pn= 0分别存在唯一正根µ,γ.因此有µ2=r1µ+p1,γ2=rnγ+pn.倘若γ >µ>0,则γ2>µ2>0,所以有

另一方面,(p1−pn)≥0,rn(µ−γ)≥0⇒(p1−pn)+rn(µ−γ)≥0与(2.11)矛盾,从而γ ≤µ.这时,为迭代求解方程(2.1),建立四元数体上的拟牛顿迭代格式如下:
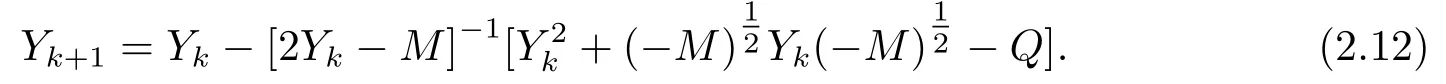
定理2设M <0,Q >0且MQ=QM,则∀Y0=tI(γ ≤t ≤µ),迭代(2.12)总收敛到(2.1)的正定解.
证类似于定理1的证明过程,考虑到方程z2+riz −pi=0(ri,pi >0)的牛顿迭代

所产生的数列(i=1,2,··· ,n)分别收敛到区间(0,pi/ri)内唯一正实数,且当γ ≤t ≤µ时t ∈(0,pi/ri),于是迭代(2.12)总收敛到(2.1)的正定解.证毕.
注3由定理2可知,当M <0,Q>0且MQ=QM时,方程(2.1)存在正定解且满足不等式.
(III)讨论M ∈SCn(Q)为不定矩阵的情况.当M是不定矩阵且Q>0时,不妨设

利用前面(II)的方法,容易知道引理2的结论仍然成立.也就是说方程z2−r1z −p1= 0与z2−rnz −pn=0分别存在唯一正根σ,τ且τ ≤σ.这时,我们可把(2.1)改写为

根据(2.14)建立四元数体上新的拟牛顿迭代格式如下:

定理3设M ∈SCn(Q),Q >0且MQ=QM,则∀Y0=tI(τ ≤t ≤σ)迭代(2.15)总收敛到(2.1)的正定解.
证由前面讨论可知,我们只需考虑方程z2−riz −pi=0(pi >0,ri ∈R)的下列牛顿迭代对于初值z0(i)=t的收敛性.

x当ri <0时,由(2.13)可知∀t ∈(0,pi/|ri|)迭代(2.16)收敛.y当ri= 0时,显然迭代(2.16)收敛.z当ri >0时,由注2可知迭代(2.16)收敛.又因为
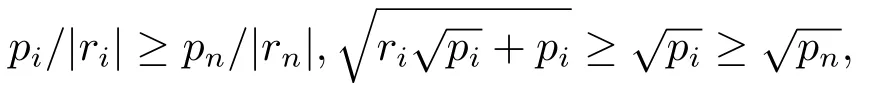
其中rn=λmin(M)<0,pn=λmin(Q)>0.令则当t ∈(0,δ)时,迭代(2.16)的所有数列{zk(i)}都收敛.所以选取Y0=tI迭代(2.15)总收敛到(2.1)的正定解.证毕.
根据(I)-(III)的讨论,利用四元数矩阵的复表示运算性质,我们对四元数体上的迭代(2.7),(2.12),(2.15)均可形成与复数域C上等价的迭代:

其中(·)σ表示四元数矩阵(·)的复表示矩阵.
实际计算时,由于四元数乘法非交换原因,我们在Matlab软件运行时只按上述(2.7-c),(2.12-c),(2.15-c)格式来计算,最后把第k次近似解Y σk还原回Yk=Yk1+Yk2j即为方程(2.1)的近似解,从而得到方程(1.1)的第k次近似正定解为根据四元数矩阵与其复表示矩阵的Frobenius范数的关系,方程(1.1)的第k次近似解余项范数为

3.数值算例
给定3个n阶正定四元数矩阵:A=In(单位矩阵),

试求方程XAX −BX=P的自共轭正定解.
解这里对任意的正整数n直接验证可知MQ=QM,因此由引理1知,方程X2−MX=Q存在自共轭正定解.
x对于M >0,Q >0可采用(2.7)或(2.7-c)建立迭代格式.根据四元数矩阵的圆盘定理[16],M的特征值分布范围是1≤λ(M)≤3,Q的特征值分布范围是3≤λ(Q)≤7.依照注2,迭代初始矩阵可选取为即有
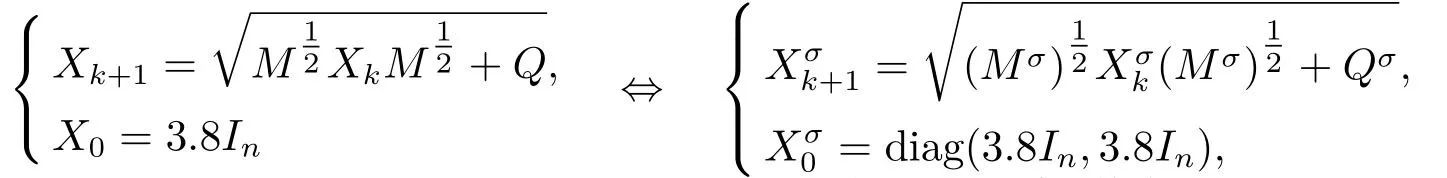
这里Mσ,Qσ分别是M=M1+M2j,Q=Q1+Q2j的复表示矩阵,其中

当n=5时,计算可得


这里Mσ,Qσ与x相同.当n=5时,计算可得

当n=200,600,1000时迭代结果见表1.
z给出一个不定四元数自共轭矩阵如下

这时可采用(2.15)或(2.15-c)来计算X2=Q的正定解.由于−0.5≤λ()≤1.5,3≤λ(Q)≤7,因此根据定理3的证明过程,迭代初始矩阵可选取为X0=δI,其中δ=即有

这里Qσ与x相同,是的复表示矩阵,其中

当n=5时,计算可得

当n=200,600,1000时迭代结果见表1.

表1 M不同情况下迭代计算结果
表1结果显示,用三种迭代对求解系统(1.1)均收敛,其中迭代(2.12-c)和(2.15-c)用较少的迭代次数就能达到预设误差精度,说明其敛速相对较高.
4.结语
非线性系统(1.1)是一个非对称二次四元数矩阵方程,本文在为自共轭矩阵且P正定条件下讨论了它的自共轭正定解.主要结果是针对四元数矩阵M分别为正定、负定、不定三种情况,构建出收敛的迭代公式,并根据各种迭代特点分析给出初始矩阵的选取方法.最后运用四元数矩阵复算子得出适应Matlab环境的迭代公式(2.7-c),(2.12-c),(2.15-c),解决四元数乘法非交换问题.数值算例表明,所给算法对求解系统(1.1)可行有效.

