NEW NON-NATURALLY REDUCTIVE EINSTEIN METRICS ON Sp(n)∗
(张绍祥)
College of Mathematics and System Science,Shandong University of Science and Technology,Qingdao 266590,China
School of Mathematical Sciences and LPMC,Nankai University,Tianjin 300071,China
E-mail:zhangshaoxiang@mail.nankai.edu.cn
Huibin CHEN(陈慧斌)
School of Mathematical Sciences,Nanjing Normal University,Nanjing 210046,China
E-mail:chenhuibin@mail.nankai.edu.cn
Shaoqiang DENG(邓少强)†
School of Mathematical Sciences and LPMC,Nankai University,Tianjin 300071,China
E-mail:dengsq@nankai.edu.cn
Abstract In this paper,we consider a class of left invariant Riemannian metrics on Sp(n),which is invariant under the adjoint action of the subgroup Sp(n−3)×Sp(1)×Sp(1)×Sp(1).Based on the related formulae in the literature,we show that the existence of Einstein metrics is equivalent to the existence of solutions of some homogeneous Einstein equations.Then we use a technique of the Gröbner basis to get a sufficient condition for the existence,and show that this method will lead to new non-naturally reductive metrics.
Key words Einstein metric;non-naturally reductive metric;compact Lie group;symplectic group
1 Introduction
A Riemannian manifold(M,g)is called Einsteinian if there is a constant ρ such that the Ricci tensor satisfies Ric(g)=ρg.Einstein metrics play an important role in Riemannian geometry and general relativity;see the survey book[5]and the articles[15,16].Classifying homogeneous Einstein metrics has been an interesting and important problem,and it has been reduced to the classification to two special cases:G-invariant Einstein metrics on homogeneous spaces G/H(see[6,7,17]),and left-invariant Einstein metrics on compact Lie groups.
As is well known,any bi-invariant Riemannian metric on a compact simple Lie group must be Einsteinian,and be globally symmetric.As a generalization of symmetric metrics,naturally reductive metrics play an important role in many areas.In 1979,D’Atri and Ziller in[12]established many important results on naturally reductive Einstein metrics on compact Lie groups,in particular,on the classical groups SO(n),SU(n)and Sp(n).From then on,many results have been established on left-invariant Einstein metrics on compact Lie groups which are non-naturally reductive.Mori initiated the study of this problem by showing that there exist non-naturally reductive left-invariant Einstein metrics on SU(n)for n≥6 in[13].Later,the authors of[2,3]got the existence of such metrics on the compact Lie groups SO(n)for n≥11,Sp(n)for n≥3,E6,E7and E8.Z.Chen and K.Liang in[10],Chrysikos and Sakane in[11],and H.Chen,Z.Chen and S.Deng in[8]also obtained some new non-naturally reductive Einstein metrics on exceptional simple Lie groups.Recently,Z.Yan and S.Deng found a new method for constructing left invariant non-naturally reductive Einstein metrics on compact simple Lie groups through the study of standard triples,and,in particular,established the existence of such metrics on SO(8)and SO(10)in[18].Later on,Z.Chen and H.Chen in[9]found two new non-naturally reductive Einstein metrics on Sp(n),and gave lower bounds of the number for Sp(n)(n≥4).However,up until now,examples of non-naturally reductive Einstein metrics have been few,and it is still important to find more new examples.
In this paper,we consider left-invariant Einstein metrics on Sp(n)and find new examples by showing the following:
Theorem 1.1For n≥4,the compact simple Lie group Sp(n)admits at least one new Ad(Sp(n−3)×Sp(1)×Sp(1)×Sp(1))-invariant Einstein metric,which is non-naturally reductive.
In Section 2,we recall some fundamental results and give a decomposition of the Lie algebra of the Lie group Sp(n).In Section 3,we calculate the Ricci tensor for Lie group Sp(n)in detail.Finally,in Section 4,based on the Ricci tensor formula in[14]and the technique of the Gröbner basis,we prove that Sp(n)for n≥4 admits a new Ad(Sp(n−3)×Sp(1)×Sp(1)×Sp(1))-invariant non-naturally reductive Einstein metric.
2 The Ricci Tensor of Reductive Homogeneous Spaces
In this section,we recall some definitions and fundamental results.We will also describe a decomposition of the Lie algebra of Sp(n)which will be useful in this paper.
Let G be a compact semisimple Lie group,let K be a connected closed subgroup of G and letandbe the corresponding Lie algebras.The Killing form B of g is negative definite,so we can define an Ad(G)-invariant inner product−B on g.LetL be a reductive decomposition ofwith respect to−B so that[k,m]⊂m andWe assume that m can be decomposed into mutually non-equivalent irreducible Ad(K)-modules as follows:
Then any G-invariant Riemannian metric on G/K can be expressed as
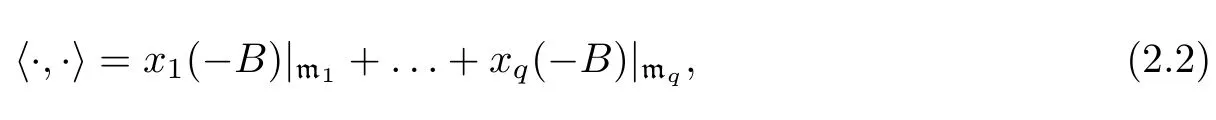
where x1,...,xqare positive real numbers.
The Ricci tensor r of a G-invariant Riemannian metric on G/K is of the same form as in(2.2);that is,there exist real numbers y1,...,yqsuch that
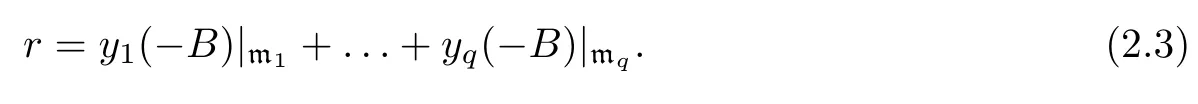
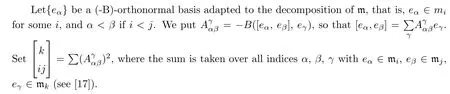
With respect to the metric given above,we define

Let dk=dimmk.Then we have the following:
Lemma 2.1([14]) The components r1,...,rqof the Ricci tensor r of the metric of form(2.2)on G/K are given by
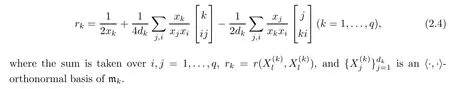
Let K=Sp(k1)×Sp(k2)×Sp(k3)×Sp(k4)and write G=Sp(n)=Sp(k1+k2+k3+k4),where k1,k2,k3,k4≥1.Obviously,K is the closed subgroup of G and the embedding of K in G is diagonal.Then the tangent space(k1+k2+k3+k4)of the symplectic group G=Sp(k1+k2+k3+k4)can be written as a direct sum of Ad(K)-invariant modules as
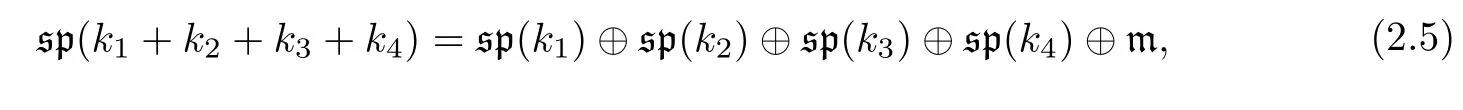
For i=1,2,3,4,we embed the Lie subalgebra
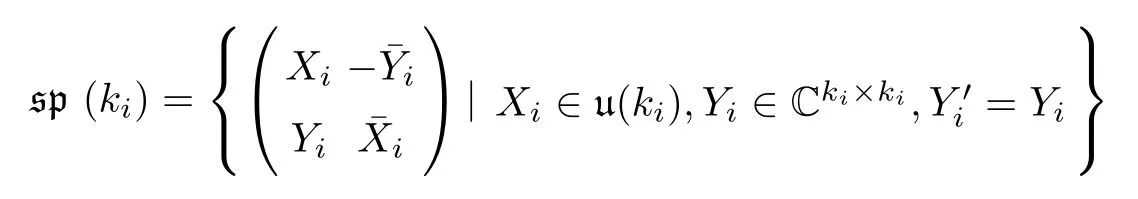
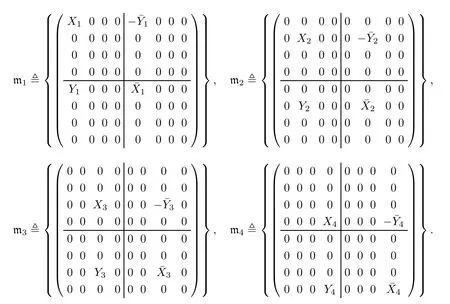

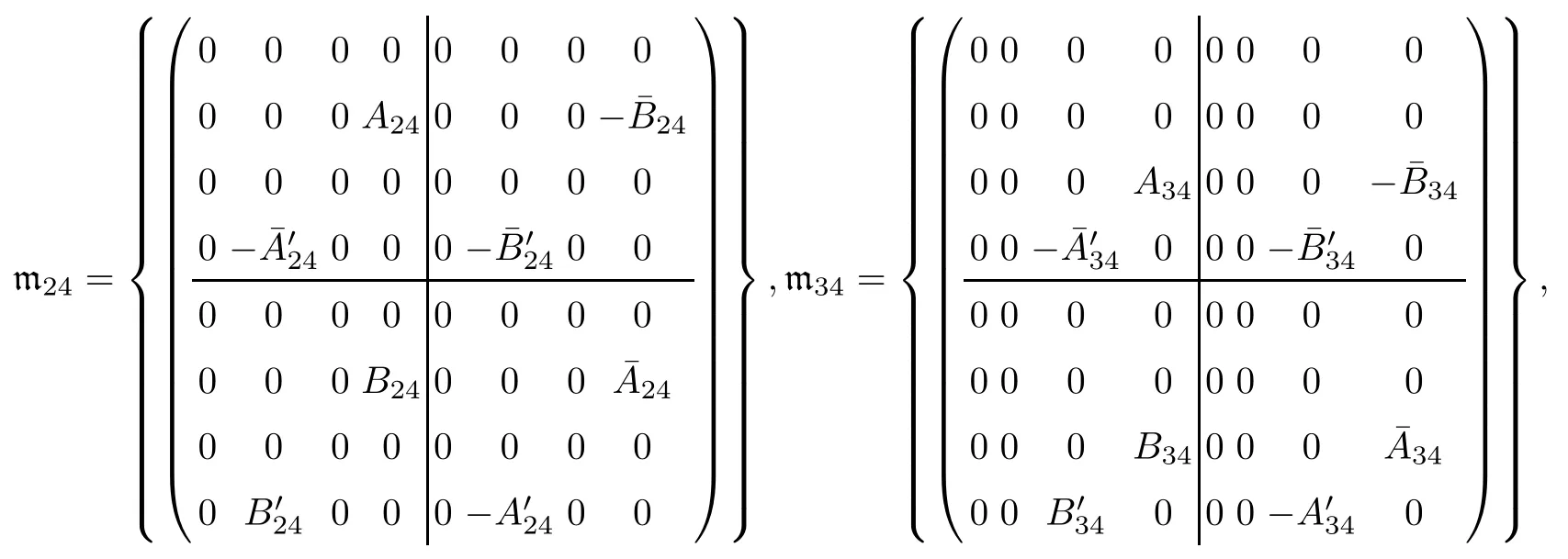
where

The subspaces mijare given as the corresponding orthogonal complements,with respect to the negative of Killing form.Note that the subspaces mijare the irreducible Ad(K)-submodules and that the irreducible submodules mijare mutually non-equivalent.
Therefore,decomposition(2.5)of the Lie algebra of the symplectic group G=Sp(k1+k2+k3+k4)is

where mjis isomorphic to sp(kj),1≤j≤4.
As a manifold,the Lie group G is diffeomorphic to the coset space

Now we consider left-invariant metrics on G which are determined by the Ad(Sp(k1)×Sp(k2)×Sp(k3)×Sp(k4))-invariant scalar products on sp(k1+k2+k3+k4),given by
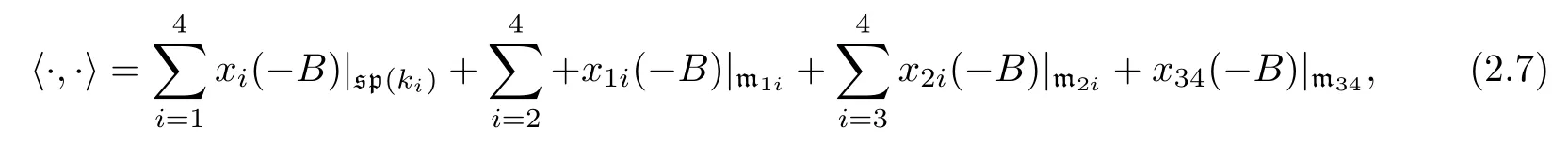
where the xi’s and xij’s are all positive real numbers.Then we have the following:
Lemma 2.2The submodules in decomposition(2.6)satisfy the following bracket relations:
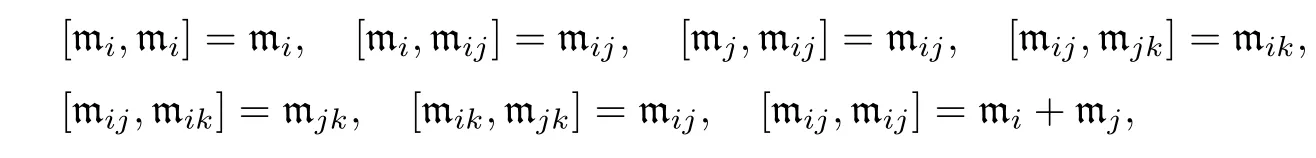
where 1≤i The proof is direct,so we omit it. It follows that the only non zero symbols(up to permutations of indices)are Denote by diand dijthe dimensions of the modules miand mij,respectively.Since dimmij=4kikj(1≤i In[12],D’Atri and Ziller investigated naturally reductive metrics among left-invariant metrics on compact Lie groups and gave a complete classification in the case of simple Lie groups.Let G be a compact,connected semisimple Lie group,and let L be a closed subgroup of G.Letbe the Lie algebra of G and l the subalgebra corresponding to L.Denote by Q the negative of the Killing form ofThen Q is an Ad(G)-invariant inner product onLet m be the orthogonal complement oflwith respect to Q.Then we have Let l=l0⊕l1⊕...⊕lpbe a decomposition oflinto ideals,whereis the center ofland li(i=1,...,p)are simple ideals of l.Letbe an arbitrary metric on. Definition 3.1A Riemannian homogeneous space(M=G/K,〈·,·〉)with a reductive complement m ofinis called naturally reductive if Theorem 3.2([12]) Under the notations above,a left-invariant metric on G of the form is naturally reductive with respect to G×L,where G×L acts on G by(g,l)y=gyl−1. Moreover,if a left-invariant metric〈·,·〉on a compact simple Lie group G is naturally reductive,then there is a closed subgroup L of G and the metric〈·,·〉is given by form(3.1). For the Lie group Sp(n),we consider Ad(Sp(k1)×Sp(k2)×Sp(k3)×Sp(k4))-invariant metrics of form(2.7).We first prove the following: Proposition 3.3If a left invariant metric〈·,·〉of form(2.7)on Sp(n)is naturally reductive with respect to Sp(n)×L for some closed subgroup L of Sp(n),then one of the following holds: 1)x1=x2=x12,x13=x14=x23=x24=x34; 2)x1=x2=x12,x3=x4=x34,x13=x14=x23=x24; 3)x1=x2=x3=x12=x13=x23,x14=x24=x34; 4)x1=x2=x4=x12=x14=x24,x13=x23=x34; 5)x1=x3=x13,x12=x14=x23=x24=x34; 6)x1=x3=x13,x2=x4=x24,x12=x14=x23=x34; 7)x1=x3=x4=x13=x14=x34,x12=x23=x24; 8)x1=x4=x14,x12=x13=x23=x24=x34; 9)x1=x4=x14,x2=x3=x23,x12=x13=x24=x34; 10)x2=x3=x23,x12=x13=x14=x24=x34; 11)x2=x3=x23,x1=x4=x14,x12=x24=x13=x34; 12)x2=x3=x4=x23=x24=x34,x12=x13=x14; 13)x2=x4=x24,x12=x14=x23=x13=x34; 14)x3=x4=x34,x12=x13=x14=x23=x24; 15)x12=x13=x14=x23=x24=x34. Using Lemma 2.1 and(2.8),we get the following: Proposition 3.5The components of the Ricci tensor r for the left-invariant metric〈·,·〉on Sp(n)defined by(2.7)are given as where i,j=1,2,3,4 and i/=j. We recall the following result by A.Arvanitoyeorgos,V.V.Dzhepko and Yu.G.Nikonorov: Lemma 3.6([1,4]) The following relations hold: Here,a,b,c=1,2,3,or 4 and(a−b)(b−c)(c−a)/=0. Combining the above results,we get the components of the Ricci tensor for the metrics(2.7). Proposition 3.7The components of the Ricci tensor r for the left-invariant metric〈·,·〉on G defined by(2.7)are given as where i,j=1,2,3,4 and i/=j. In this section,we give a detailed proof of Theorem 1.1.Consider the case of k1=n−3,k2=1,k3=1,k4=1.By the definition of rkin[14],we only need to deal with the equations Setting we can reduce equations(4.1)to Then finding Einstein metrics of form(2.7)is reduced to finding positive solutions of the system of equations(4.2).It is easy to deduce the system of algebraic equations Consider the polynomial ring R=Q[z,x2,x1,x23]and the ideal I generated by{r1−r2,r2−r12,r12−r23,z(x2−x23)x1x2x23−1}.We need to find positive solutions of the system with x2/=x23.With the help of a computer,we obtained a Gröbner basis containing the polynomials{f(x23),g1(x23,x1),g2(x23,x2)},where f(x23)is the polynomial of x23given by Now we need to prove that f(x23)has a positive root and that x23/=1.We can show that there is a positive solution for n≥4 by f(0)=1682+3364n>0, f(1)=12n2+21n3−6n4, f(2)=−11542+31600n−30016n2+13456n3−2944n4+256n5>0,and for n≥4, Thus,for non-naturally reductive Einstein metrics,we see that,for n≥33,there are four positive solutions:x23=a,x23=b,x23=c and x23=d,with and that,for 5≤n≤32,there are two positive solutions:x23=a/=1(together with f(1)<0)and x23=d>1,with Therefore,the equation f(x23)=0 has at least one positive root for n≥4.On the other hand,g1(x23,x1)is the polynomial of x23and x1given by and g2(x23,x2)is the polynomial of x23and x2given by Since there exists a real root x23=a23of f(x23)=0,there is also a real solution x1=a1for g1(x23,x1)=0 and a real solution x2=a2for g2(x23,x2)=0. Now we show that the real solutions x1=a1of g1(x23,x1)=0 and x2=a2of g2(x23,x2)=0 are positive.With the help of a computer,we obtained a Gröbner basis containing the polynomial f1(x1)of x1given by and the polynomial f2(x2)of x2given by If n≥4,then the coefficients of the polynomial f1(x1)and f2(x2)are positive for even degree terms and negative for odd degree terms,so f1(x1)and f2(x2)must have positive real solutions.Since the obtained solution{x1,x2,x3,x4,x12,x13,x14,x23,x24,x34}of system(4.2)satisfies the conditions we conclude,by Proposition 3.3,that these metrics are not naturally reductive.Obviously,these metrics are not given in[4].This completes the proof of Theorem 1.1.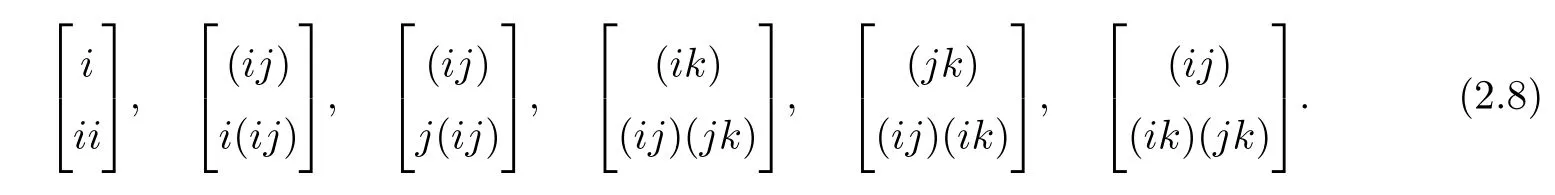
3 Naturally Reductive Metrics and the Ricci Tensor on the Compact Lie Groups Sp(n)

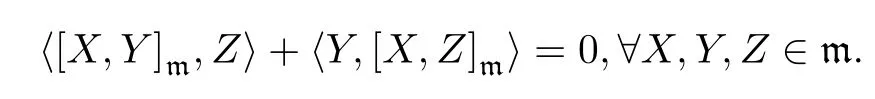
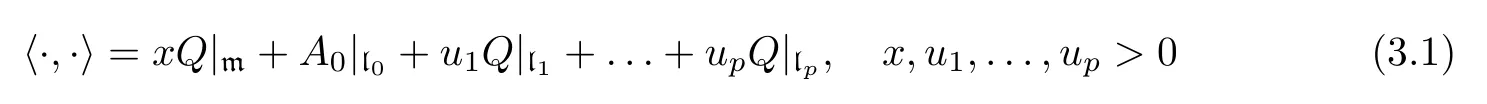

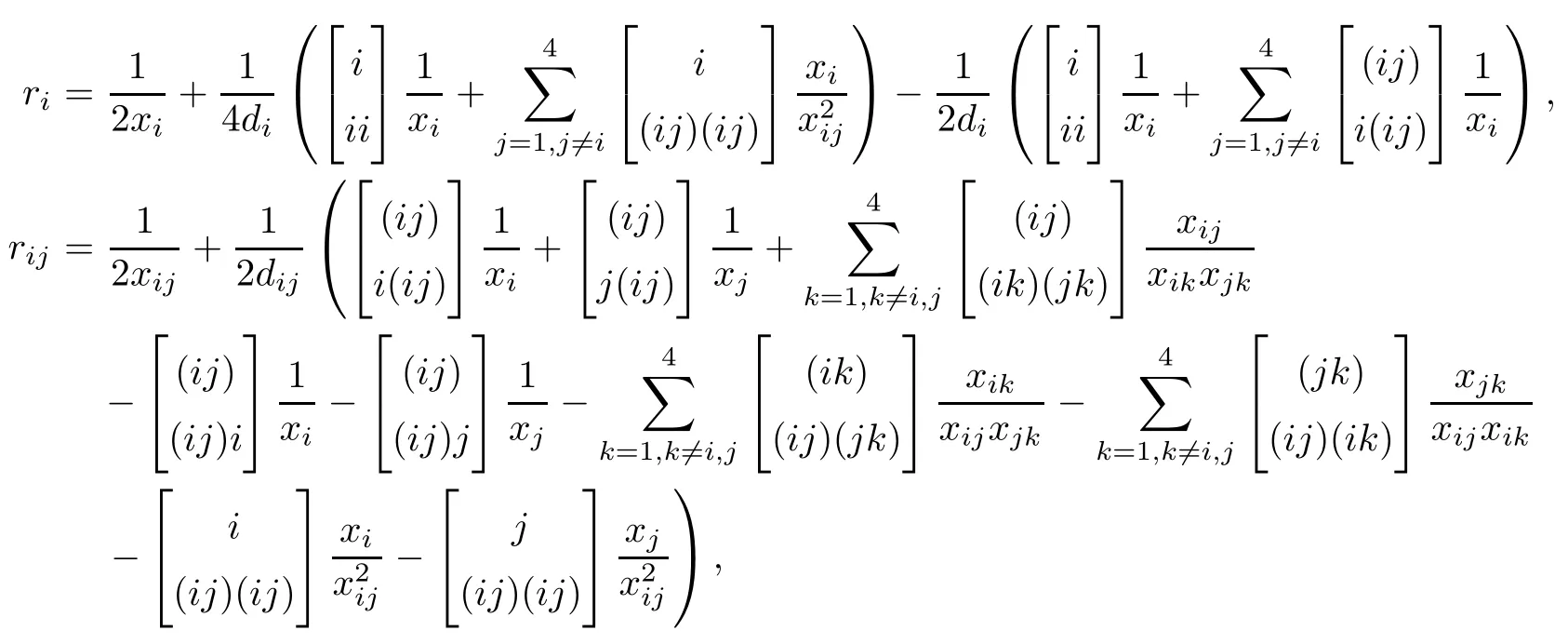
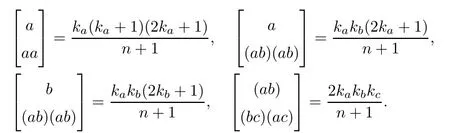

4 New Left-Invariant Einstein Metrics on Sp(n)
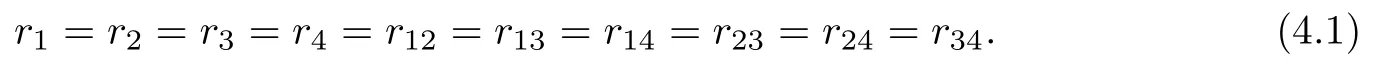



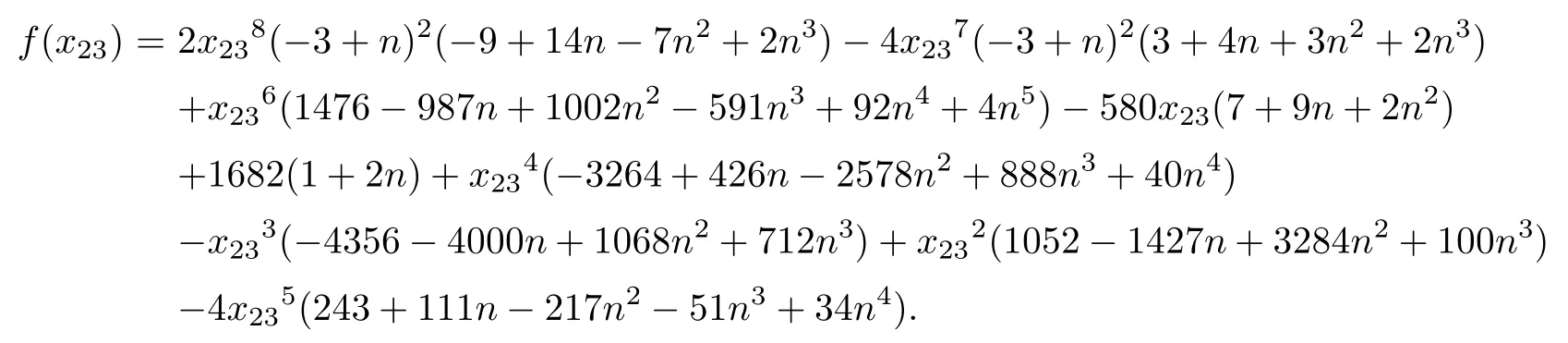

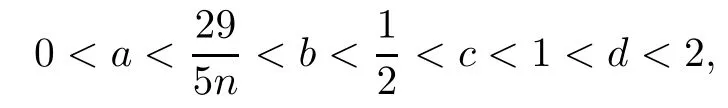
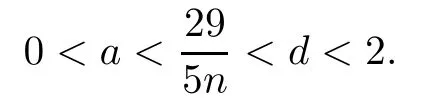



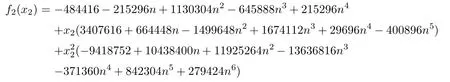


 Acta Mathematica Scientia(English Series)2021年3期
Acta Mathematica Scientia(English Series)2021年3期
