共振情形下一类非合作反应堆数学模型正解的存在性

陈瑞鹏，刘佳音，张光晨

(北方民族大学数学与信息科学学院，宁夏银川750021)

1.引言

本文研究二阶非合作微分系统

正解的存在性，其中c，d为正常数，非线性项f∈C([0，1]×[0，∞)，R)且g∈C([0，∞)，[0，∞)).因此，系统(1.1)是一个半正系统，同时由Neumann边界条件易见系统(1.1)为共振系统.

系统(1.1)与反应扩散系统

的稳态形式有着紧密联系.反应扩散系统(1.2)旨在描述密闭容器中与中子通量、反应堆温度等因素密切相关的核反应过程，其中Ω是Rn(n≥1)中具有C2+θ(θ∈(0，1))光滑边界∂Ω的有界连通区域，且代表密闭容器，n为∂Ω上的单位外法向量.实际应用方面，未知函数u和v分别表示中子通量与反应堆的温度，b，c，d均为常数且满足b∈[0，∞)，c，d∈(0，∞)，u0，v0∈C为初始条件.通过添加温度的扩散与线性反馈，模型(1.2)改进了由Kastenberg和Chambr[10]提出的反应堆数学模型

注意到模型(1.2)中的Neumann边界条件意味着快中子不能穿越容器壁，而且密闭容器的边界绝热，这代表更加贴近实际的情形.

近年来，诸多学者对模型(1.3)正解的存在性及相关性质做了深入研究，并获得了许多深刻的结果[1，7，10，12，14－15].同时，多位学者致力于研究模型(1.3)在一维情形下正解的存在性问题，如WANG和AN[16－18]，LI和LI[11]，CHEN和MA[3－4]等.然而据我们所知，上述大多数文献聚焦于研究带有Dirichlet边界条件的模型(1.3)，其中Dirichlet边界条件意味着密闭容器的边界上没有快中子且恒温，是一种较为理想的情形，但是在Neumann边界条件下的研究成果相对较少.此外，文[3-4，16-18]只对模型的非共振情形进行了研究，而且所得正解的存在性结果极大程度上依赖于非线性项的正性.鉴于此，本文将在共振情形下建立非合作半正系统(1.1)正解的存在性结果.本文总假设

(H1)f∈C([0，1]×[0，∞)，R)，g∈C([0，∞)，[0，∞)).

注1.1(H1)蕴含了非线性项f是变号且下无界的，这将对系统(1.1)正解存在性的研究带来较大困难.此外，本文将首次建立共振情形下反应堆数学模型正解的存在性及全局分歧结果，所得结论将进一步丰富反应堆数学模型的相关理论.对于其它半正问题和共振问题的研究，可参见文[2，8-9，13，19]等.

本文结构作如下安排:在第二部分，将给出一些所需的符号及预备知识;第三部分将叙述并证明系统(1.1)正解的存在性定理，同时给出一些相关结果和注记.

2.预备知识

若函数p∈C[0，1]在[0，1]上严格为正，则记为p≫0.令K(t，s)为边值问题

的格林函数，则不难验证K(t，s)＞0，∀(t，s)∈[0，1]×[0，1].此时，

等价于算子方程

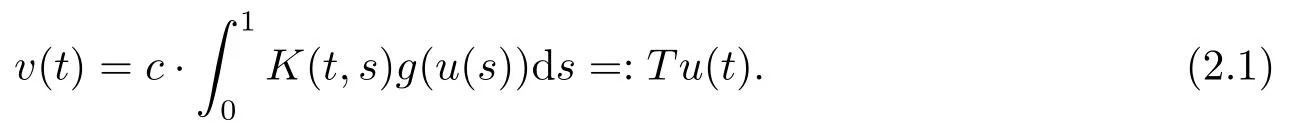
由假设(H1)易知T:C[0，1]→C[0，1]是一个全连续算子，而且系统(1.1)可转化为

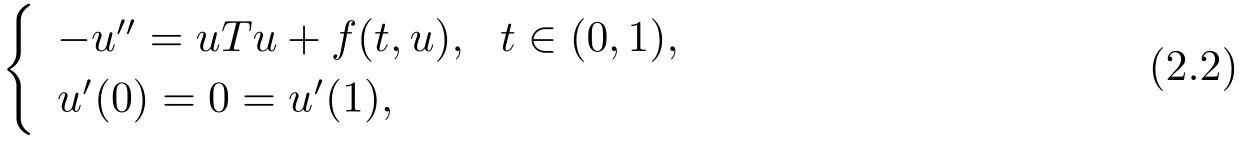
这显然是一个共振问题.

在后续讨论中，给定函数

我们将研究与(2.2)等价的积分微分方程

事实上，若问题(2.4)存在一个正解u，则由(H1)和(2.1)可知原系统(1.1)必存在正解(u，v).这里称(u，v)为系统(1.1)的一个正解，若(u，v)满足(1.1)且u≫0，v≫0.众所周知，问题(2.4)等价于积分方程

其中G(t，s)为线性边值问题

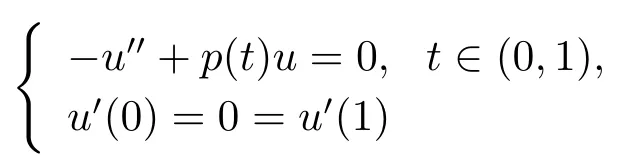
的格林函数.显然，G(t，s)在[0，1]×[0，1]连续且

令

则σ∈(0，1).定义锥

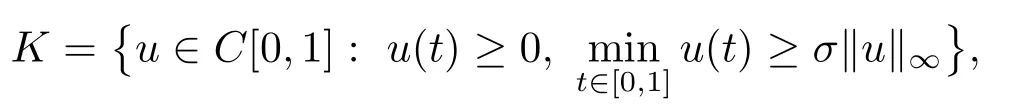
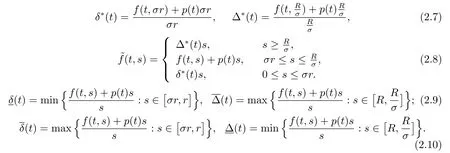
下面，我们给出本文所采用的主要工具.

假设E是实的Banach空间，其范数为‖·‖.假设K是空间E中的一个锥.称非线性映射A:[0，∞)×K→E是正的，若它满足A([0，∞)×K)⊂K.称上述映射A为K-全连续的，若A连续且把[0，∞)×K中的有界子集映射为空间E中的相对紧集.称定义于E上的线性正算子V是算子A的线性弱函数，若它满足A(λ，u)≥λV(u)，(λ，u)∈[0，∞)×K.记r(B)为定义在空间E上的连续线性算子B的谱半径.

引理2.1[5]若下列条件成立:

(i)锥K有非空内部且满足;

(ii)A:[0，∞)×K→E是一个正的K-全连续算子.

且A(λ，u)=λBu+F(λ，u)，其中B:E→E是r(B)＞0的线性强正紧算子，F:[0，∞)×K→E满足当‖u‖→0时，‖F(λ，u)‖=°(‖u‖)对λ局部一致地成立.

则在

中存在无界连通子集C，使得(r(B)－1，0)∈C.进一步，若存在A的线性弱函数V和(μ，y)∈(0，∞)×K，使得‖y‖=1及μV y≥y成立，则C位于S∩([0，μ]×K)中.

方便起见，记λ*(η)为特征值问题

的主特征值，其中函数p由(2.3)给出.由Krein-Rutman定理[6]可知当η≫0时λ*(η)＞0.此外，λ*(η)是简单的且对应的特征函数满足ψ*(η)≫0.

3.主要结果及证明

为了叙述本文的主要结果，假设

(H2)存在正常数R＞r，使得

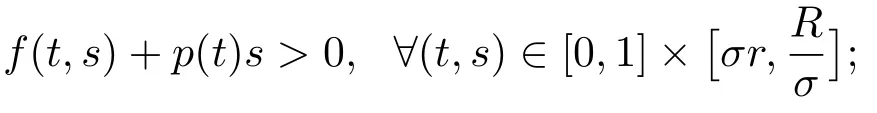
定理3.1假设(H1)，(H2)，(H3)成立.若条件

之一满足，则系统(1.1)至少存在一个正解.

证我们只证明情形(i)，情形(ii)的证明完全类似.

考虑辅助问题

其中λ∈[0，∞)为参数.由第二部分的讨论易知(3.1)等价于算子方程

运用假设(H2)，(H3)并结合函数～f的定义，不难验证A(K)⊆K且A:K→K是一个全连续算子.由(2.8)易得

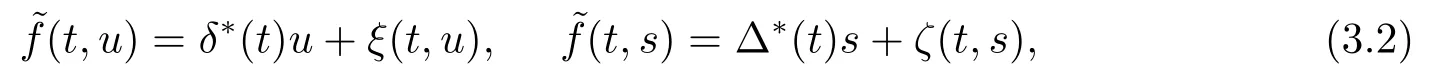
其中

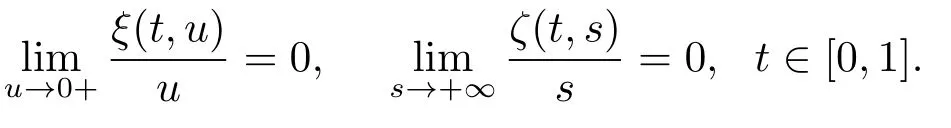
从而(3.1)可改写为

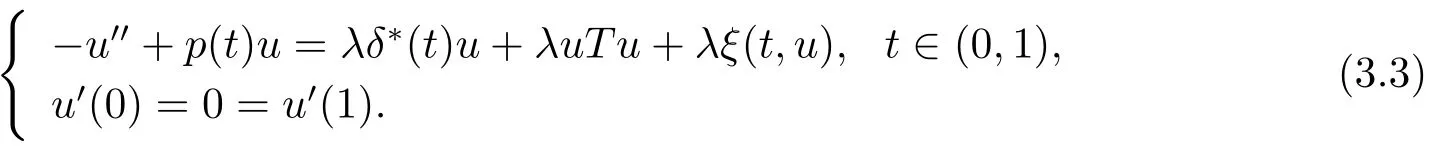
定义Banach空间E=u∈C1[0，1]:u′(0)=0=u′(1)，其范数为‖u‖=max{‖u‖∞，‖u′‖∞}.记

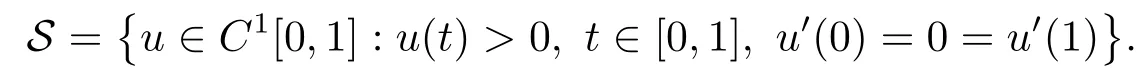
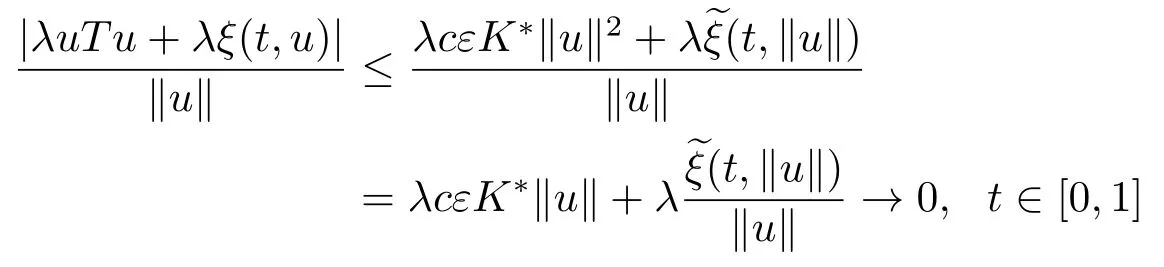
对λ局部一致地成立，其中

因此，由引理2.1可知存在(3.3)解的连通分支C，它在S中连接(λ*(δ*)，0)到无穷远处.此外，C{(λ*(δ*)，0)}⊂S.

下面，分两步来完成本定理剩余部分的证明.

第一步连通分支C在S中连接(λ*(δ*)，0)与(λ*(Δ*)，∞).

事实上，若能够证明C在S中连接(λ*(δ*)，0)与(λ*(Δ*)，∞)，则C必会穿过超平面{1}×E，从而问题(3.3)至少存在一个正解(1，u).

假设{(λk，uk)}⊂C且满足

我们宣称{λk}有界.反设λk→∞，k→∞.因为(λk，uk)∈C，所以

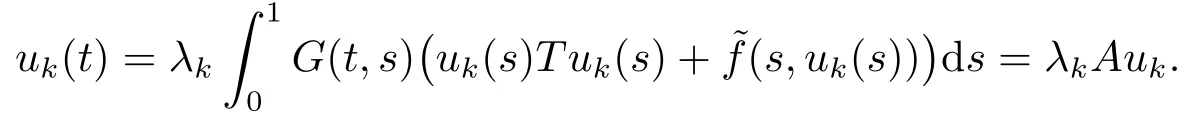
这与‖vk‖∞=1矛盾.因此{λk}有界.

此时，由(3.4)及上述宣称可得‖uk‖→∞，k→∞.进一步，运用假设(H1)-(H3)，并通过与文[3]中引理2.5证明中类似的讨论可知当‖uk‖→∞时必有‖uk‖∞→∞，从而{(λk，uk)}满足

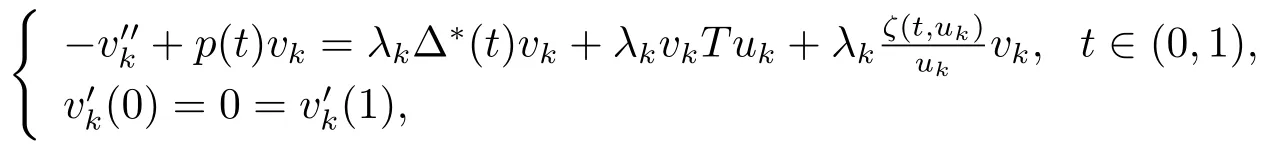
这等价于

借助(2.8)及(3.2)，经简单估计可得

这表明存在不依赖于k的函数χ∈C[0，1]，使得

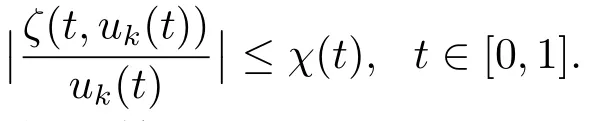
此外，由假设(H3)易得{Tuk}有界.于是，

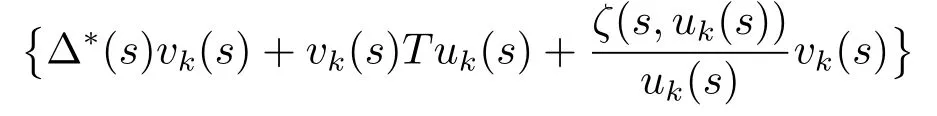
在空间C[0，1]中一致有界.容易看到

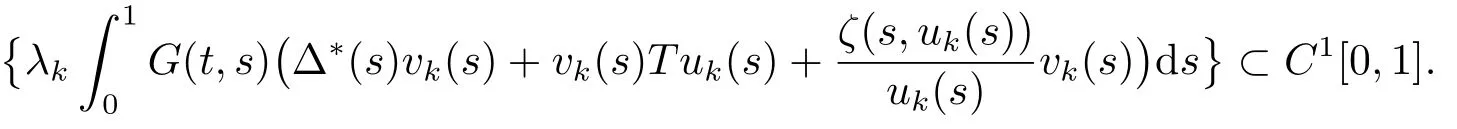
又因为C1[0，1]紧嵌入C[0，1]，故存在{vk}的子列(仍记为自身)及∈C[0，1]，∈[0，∞)，使得vk→且λk→k→∞.由假设(H3)及Lebesgue控制收敛定理可得

第二步u是共振问题(2.2)的解.

显然，只需证明

不存在能够满足‖u‖∞＜r或的正解u.事实上，若上述结论成立，则由函数的定义可得从而(3.5)将退化为原共振问题(2.2).

反设(3.5)存在一个满足‖u‖∞＜r的正解u，则由(2.8)及(2.9)可得

因为

且

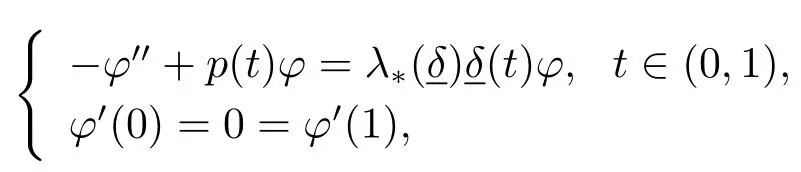
其中φ是主特征值对应的主特征函数.显然，φ≫0.运用(3.6)和假设(H1)，并通过简单的积分运算估计可得

因为u是(3.5)的正解，所以

又因为

其中ψ为λ*对应的特征函数且显然满足ψ≫0.由(3.7)和假设(H3)可得

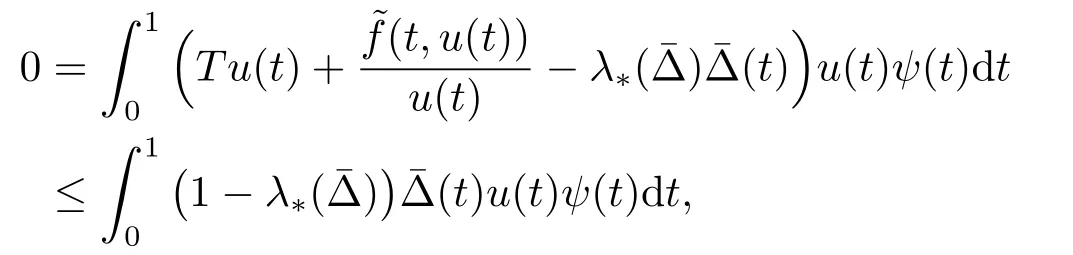
故这与假设矛盾.

综上所述，共振问题(2.2)存在一个正解u.进一步，由(2.1)可知原系统(1.1)至少存在一个正解(u，v).

最后，我们给出一些相关结果.

若考虑快中子不能穿越容器壁且反应堆与外界有热交换的情形，则适当的边界条件为

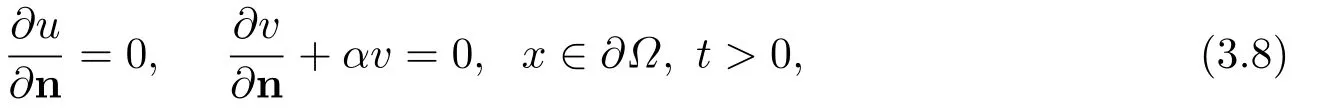
其中α＞0为热交换系数.相应地，有非合作系统

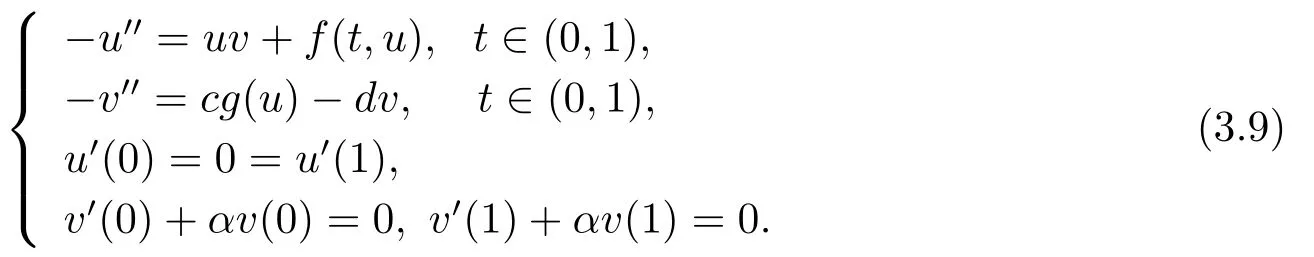
在(H1)-(H3)和一些自然的假设之下，通过与本文第二部分以及定理3.1的证明中完全类似的讨论，我们不难得到

定理3.2假设(H1)-(H3)成立.若条件

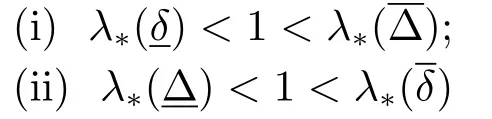
之一满足，则系统(3.9)至少存在一个正解.

注3.1对于带Neumann边界条件或边界条件(3.8)的椭圆系统

本文所采用的讨论方法仍然适用于研究其径向正解的存在性.