一类混合型Cucker-Smale模型的有限时间集群

吴俊滔，王晓，刘易成

(国防科技大学数学系，湖南长沙410073)

1.引言

为了刻画自然界中生物群体的集群行为和社会科学中语言的形成等问题，基于牛顿力学原理，2007年Cucker和Smale提出并研究了如下N个智能体构成的Cucker-Smale模型[1－2](下面简记为CS模型)的集群行为:

其中xi，vi∈Rd，d为空间维数，α代表智能体间整体的相互作用强度，(xi，vi)代表第i个智能体的位移和速度，i=1，2，···，N，交流函数aij(r)=ψ(r)/N，ψ(r)=(1+r2)－β，r≥0，β≥0.

由于CS模型的普适性，引起各领域众多学者的研究兴趣.2009年，基于显式Lyapunov方法，HA等人[3]改进了系统(1.1)实现集群行为的条件，并首次给出条件时间渐近集群和无条件时间渐近集群(以下简称条件集群和无条件集群)的相关概念.

基于有限时间稳定性的现实意义，HAN[4]考虑一个新的非Lipschitz连续系统模型，证明了在一定条件下，系统在有限时间内形成集群.一方面，HAN[4]要求系统的交流函数是某个单调递减且有正下界的连续函数，但在经典的CS模型(1.1)中，并未要求交流函数有正的下界，且交流函数的有界性就意味着相对位置的有界性，这也恰恰是证明系统形成集群的关键.另一方面，在促进系统形成集群的过程中，是非Lipschitz项起决定作用还是Lipschitz项起决定作用，都是非常值得研究的问题.

受Cucker[1－2]和HAN[4]工作的启发，本文研究一类带有非Lipschitz连续项和Llipschitz连续项混合的CS模型，其描述如下:

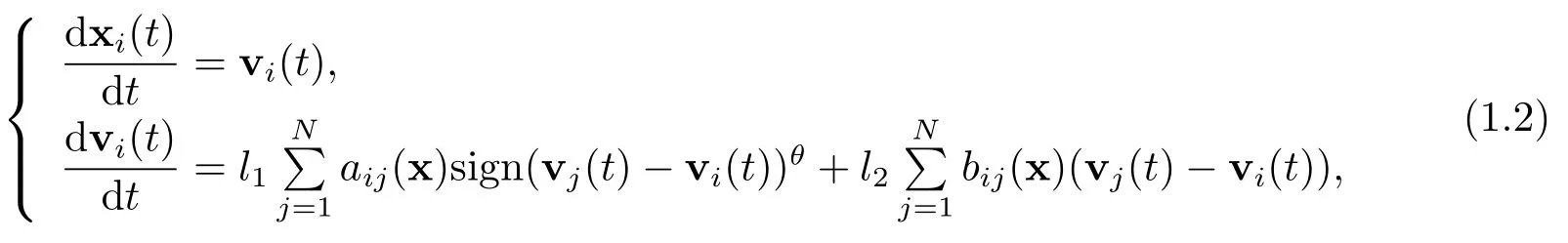
初始条件为:

其中l1，l2为非负数，且不能同时为0，x=(x1，x2，...，xN)T∈RN×d，v=(v1，v2，...，vN)T∈RN×d，sign(vj(t)-vi(t))θ=(sign(vj1-vi1)|vj1-vi1|θ，···，sign(vjd-vid)|vjd-vid|θ)，sign:R→{-1，0，1}为符号函数，0＜θ＜1，d为空间维数，aij(x)=φ(‖xi-xj‖)，bij(x)=ψ(‖xi-xj‖)，φ(·)，ψ(·)为[0，+∞)上单调递减的非负连续函数.记vi(t))θ和则易知V1是非Lipschitz连续的，V2是Lipschitz连续的.

注1当l1＞0，l2=0时，即为Han[4]中的模型，当l1=0，l2＞0时，即为经典的CS模型[1－2].

本文通过构造Lyapunov函数和建立耗散微分不等式，在去掉文[4]交流函数有正的下界的要求后，证明了系统(1.2)能够形成有限时间集群，同时也获得了系统(1.2)有限时间集群行为的发生主要由非Lipschitz连续项决定和Lipschitz连续项影响系统有限时间集群时间大小的相关结果.

2.预备知识

为了获得本文的主要结果，下面首先给出系统可以形成集群和有限时间集群的定义以及几个辅助性引理.

定义2.1[3]设为系统(1.1)在给定初值条件下的解，dX(t)和dV(t)分别表示在t时刻系统中个体之间位移和速度大小之差的最大值，即

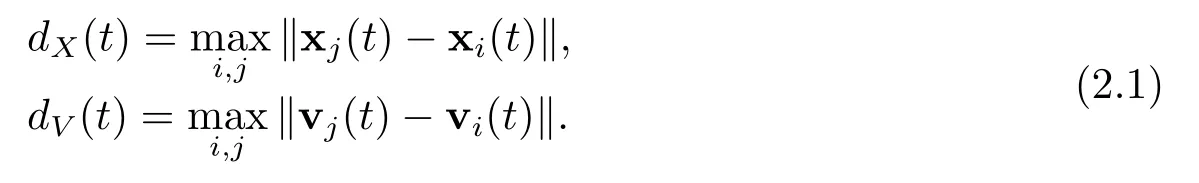
称该系统可以形成集群，若系统的所有解满足

称该系统可以有限时间形成集群，若存在正数T＞0，使得当t≥T时，有

引理2.1[7]设a1，a2，···，an＞0，给定正数r，p，当r＜p时，有

引理2.2[7]设a1，a2，···，an＞0，当0＜p≤1时，有

引理2.3[6]设k＞0，0＜p＜1为常数，V(t)为一个正连续函数满足则对任意给定t0，当t0≤t＜t1时有V1－p(t)≤V1－p(t0)-k(1-p)(t-t0)，当t≥t1时有V(t)=0，其中.

引理2.4[5]设ψ(x)为单调递减的正连续函数，非负可导函数dX(t)，dV(t)满足

若

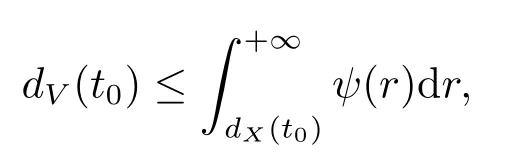
则有

受文[3]能量方法的启发，给出如下引理，也是改进文[4]中的主要结果的重要引理.

引理2.5设φ(x)为单调递减的正连续函数，0＜θ＜1，非负可导函数dX(t)，dV(t)满足

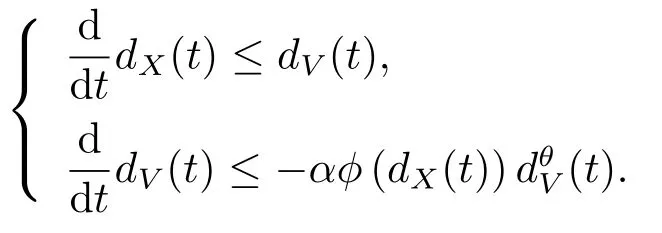
若

则有

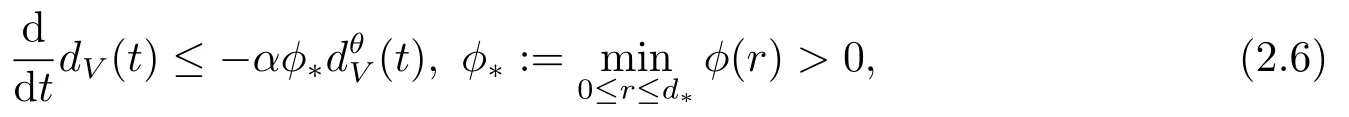
其中d*由如下式子给出

证基于HA和LIU[3]提出的耗散微分不等式以及Lyapunov方法，考虑如下能量函数

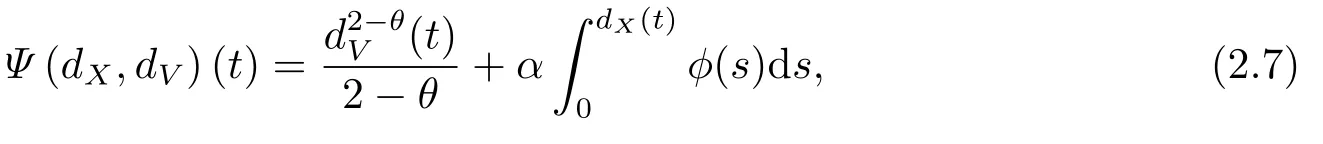
则

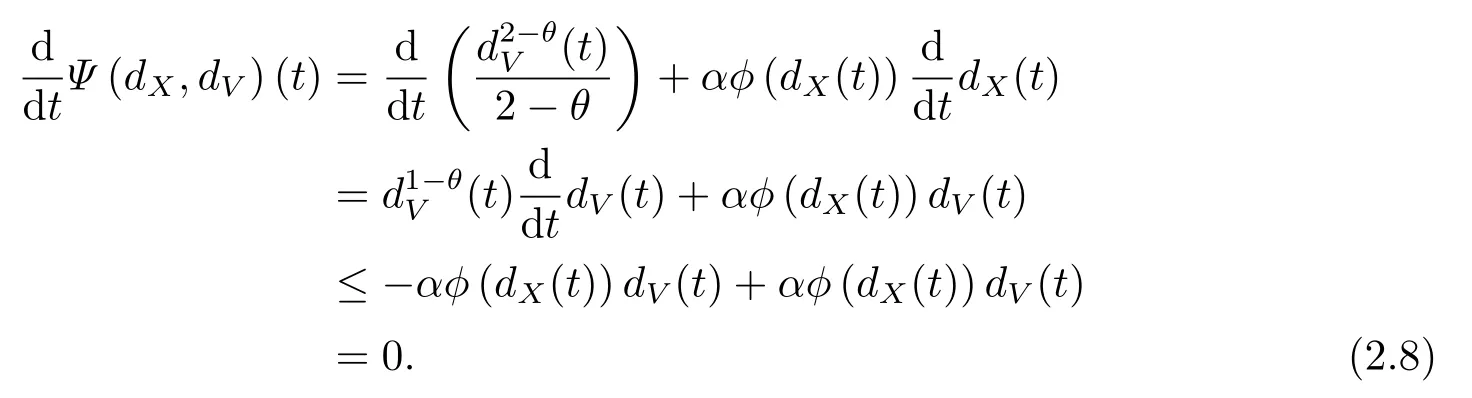
因此Ψ(dX，dV)(t)关于时间t单调递减，故对任意的t＞0，都有Ψ(dX，dV)(t)≤Ψ(dX，dV)(t0)(t0≥0为初始时刻)，即

由假设(2.5)可知，存在d*＞0(独立于t)，使得下式成立，

结合(2.9)可得

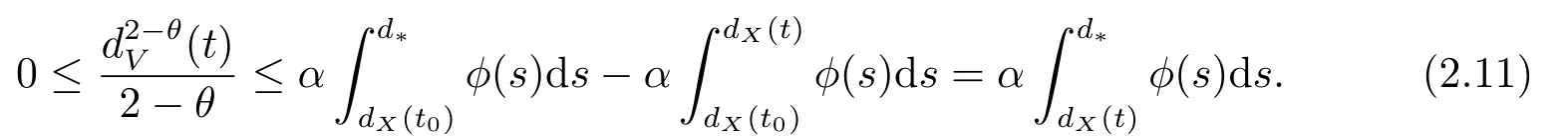
这就意味着

由φ(x)的单调性可得

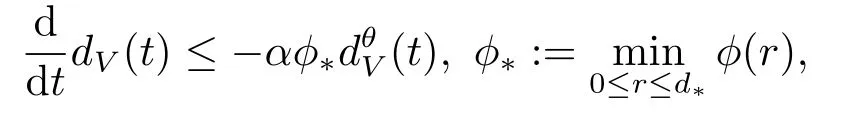
其中d*由如下式子给出

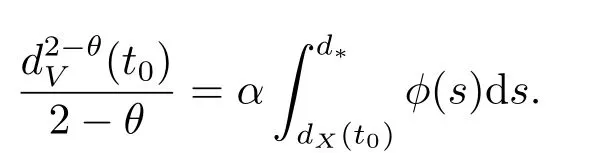
引理2.6设φ(r)，ψ(r)为单调递减的正连续函数，非负可导函数X(t)，V(t)满足

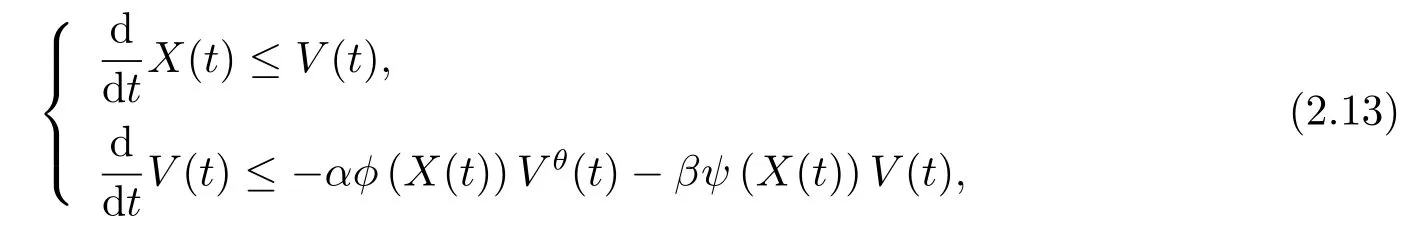
其中α，β为正常数，0＜θ＜1.对任意给定t0，若不等式

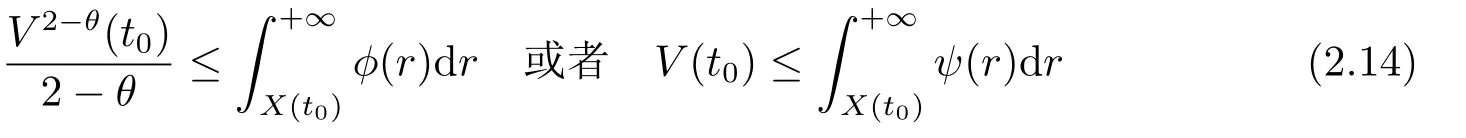
成立，则V(t)满足

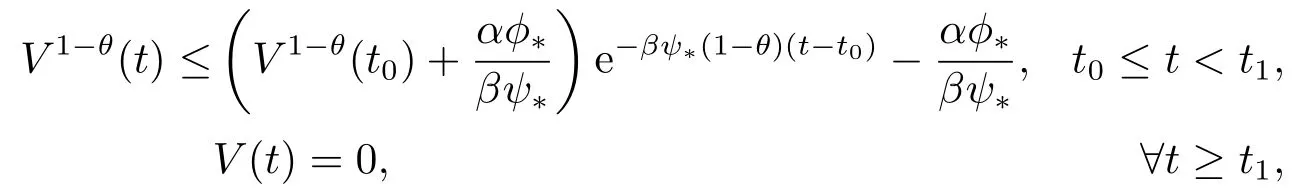
其中t1满足这里的d*由如下式子给出

证如果对(2.13)中第二个式子进行如下两种估计.

第一种方式保留上式右边V(t)项，则有

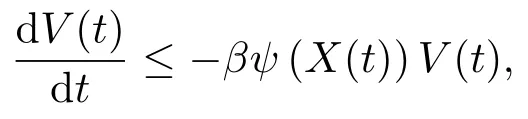
由引理2.4证明可知当

成立时，存在l*，使得对任意的t＞t0，有X(t)≤l*.

第二种方式保留上式右边V θ(t)项，则有

成立，由引理2.5证明可知当

成立时，存在s*，使得对任意的t＞t0，有X(t)≤s*.

综上，当满足条件(2.15)或者条件(2.16)时，对任意的t＞0，都存在d*，使得X(t)≤d*成立.令φ*:=根据φ(r)，ψ(r)的单调递减性可得φ(X(t))≥φ*，ψ(X(t))≥ψ*，因此X(t)，V(t)满足如下不等式组

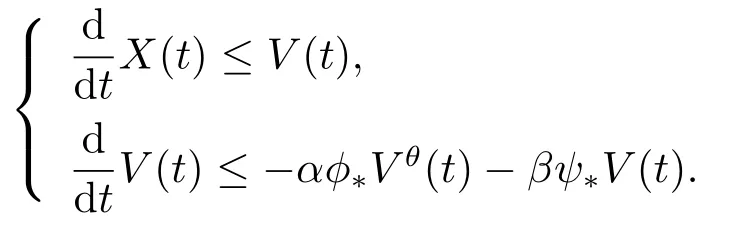
即

上式两边从t0到t积分可得

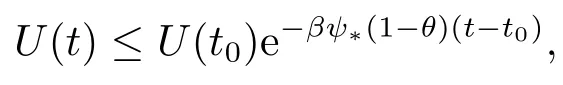
即

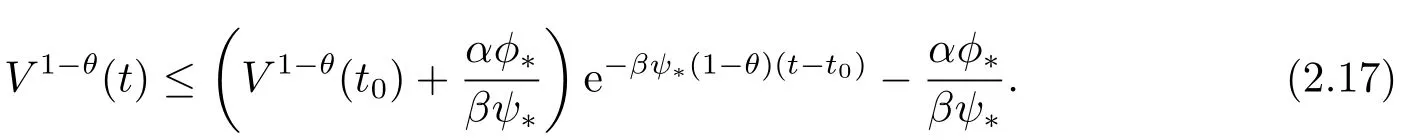
由于V1－θ(t)≥0，且(2.17)式右边单调递减，因此当t0增加到t1时，有V(t1)=0，解得

再根据V(t)的连续性可知，当t≥t1时，恒有V(t)=0(此时V(t)满足(2.17)式).

3.主要结果

本节主要研究由(1.2)刻画的多粒子群的动力学行为，并探讨其形成有限时间集群的充分条件.

为了获得本文的主要结果，下面对系统(1.2)中的位移和速度进行中心化.由aij(x)，bij(x)的对称性可得

令

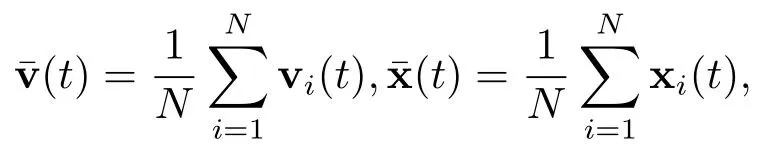
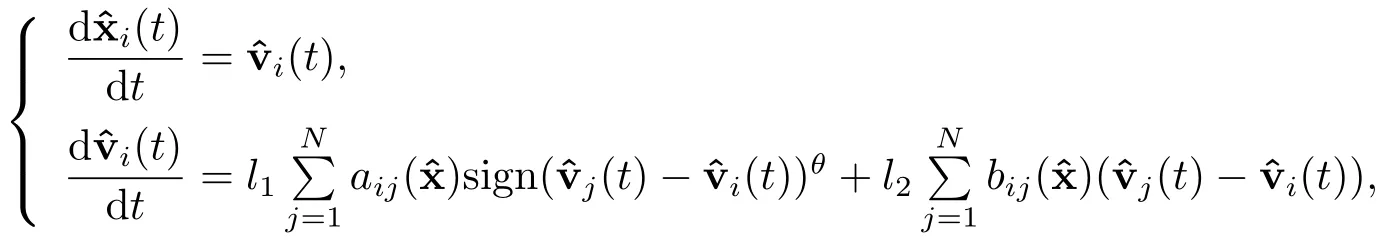
初始条件为:

且满足

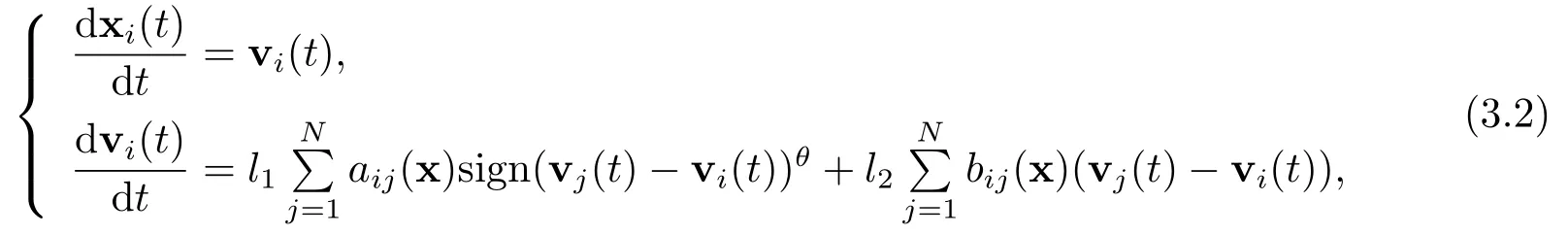
初始条件为:

并满足

设x=(x1，x2，...，xN)T∈RN×d，v=(v1，v2，...，vN)T∈RN×d为系统(3.2)的解，令

则有

同理可证

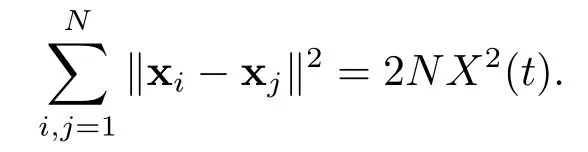
为了研究系统(1.2)的集群性，则只需研究系统(3.2)的集群性，由X(t)，V(t)的定义可知，即证X(t)，V(t)满足条件(2.2)或者(2.3).

下面通过给出系统(3.2)有限时间集群的充分条件，从而得到系统(1.3)有限时间集群的充分条件.

定理3.1考虑系统(1.2)-(1.3)，设为系统(3.2)在给定初始条件(3.3)下的解，则有

1)若l1=0，l2＞0，ψ(r)为[0，+∞)上单调递减的连续正函数，且满足

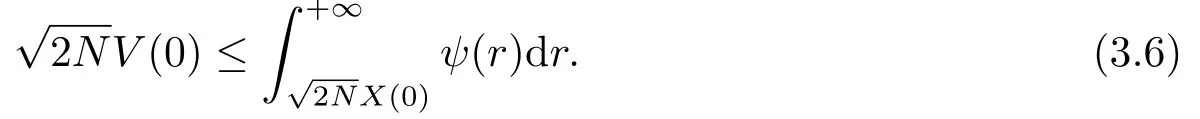
则系统(1.2)条件渐近集群.

特别地，若

则系统(1.2)无条件渐近集群;

2)若l2=0，l1＞0，φ(r)为[0，+∞)上单调递减的连续正函数，且满足

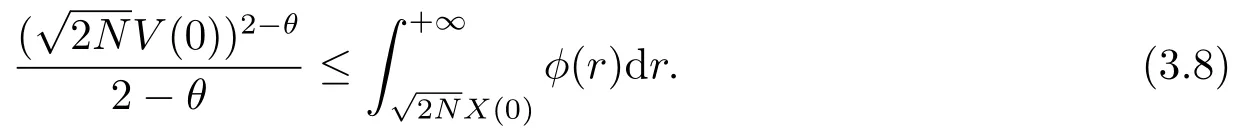
则系统(1.2)有限时间集群.有限时间集群时间为

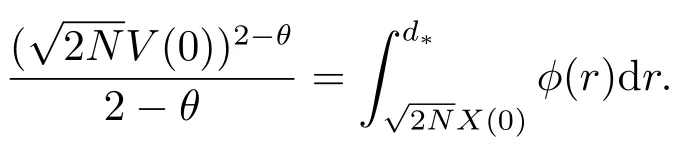
特别地，若

则系统(1.2)无条件有限时间集群;

3)若l1＞0，l2＞0，ψ(r)，φ(r)为[0，+∞)上单调递减的连续正函数，且满足

则系统(1.2)有条件有限时间集群.有限时间集群时间为

特别地，若

系统(1.2)无条件有限时间集群.

这里及本文中出现X(t)和V(t)如(3.5)式所示.

证对V2(t)求导可知

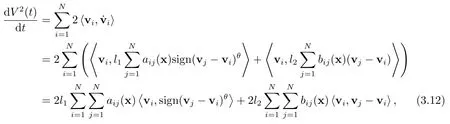
而

同理

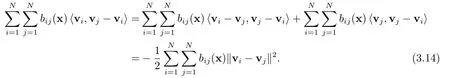
由(3.12)，(3.13)，(3.14)可得

由引理2.2可知

故有

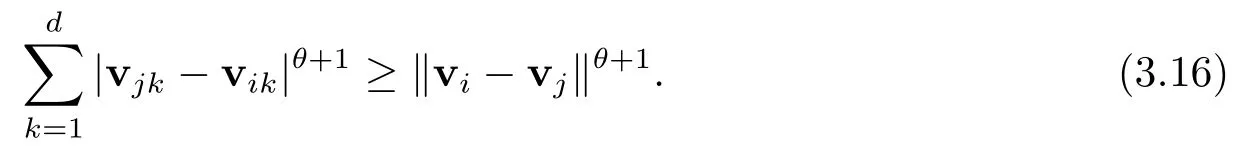
由引理2.3可知

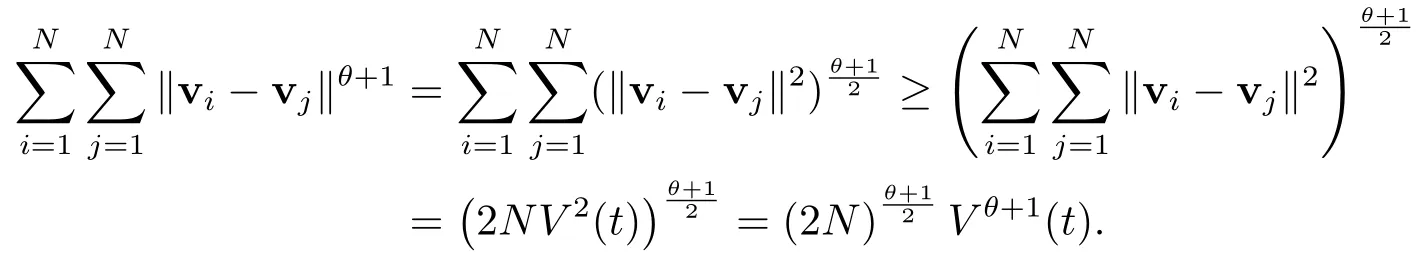
根据(3.15)和(3.16)可得

而

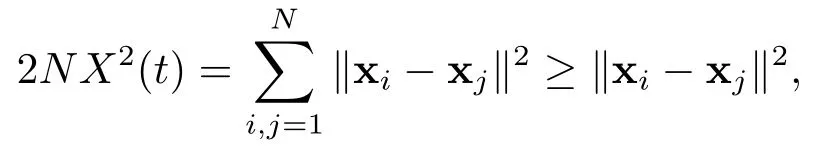
即

由假设φ(·)，ψ(·)为单调递减的连续非负函数，则有

因此有

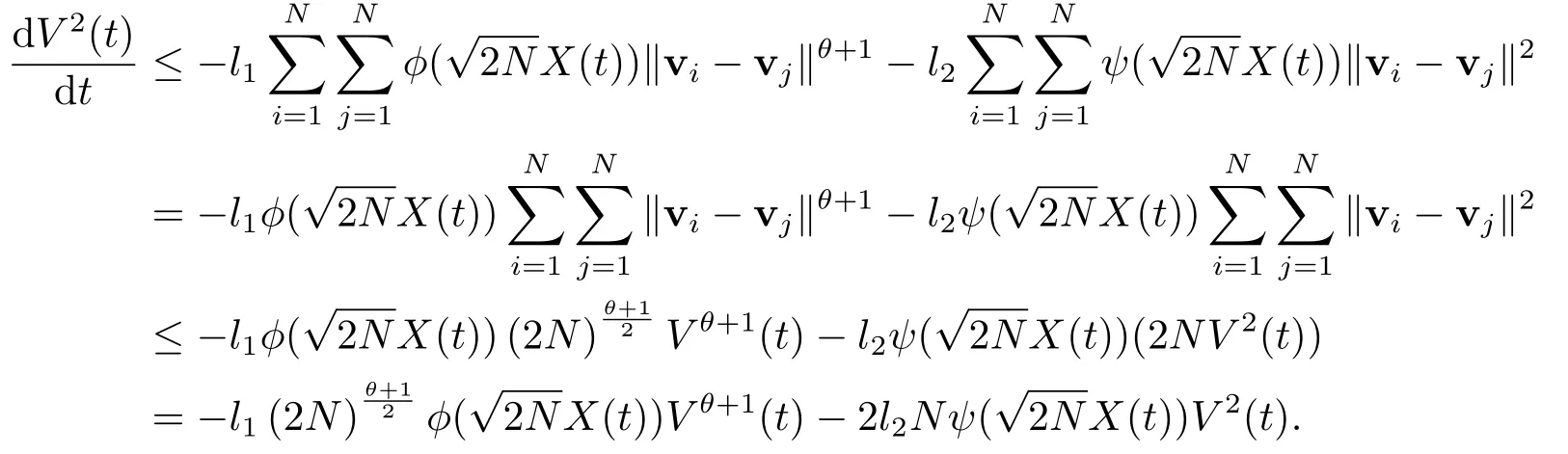
即

又

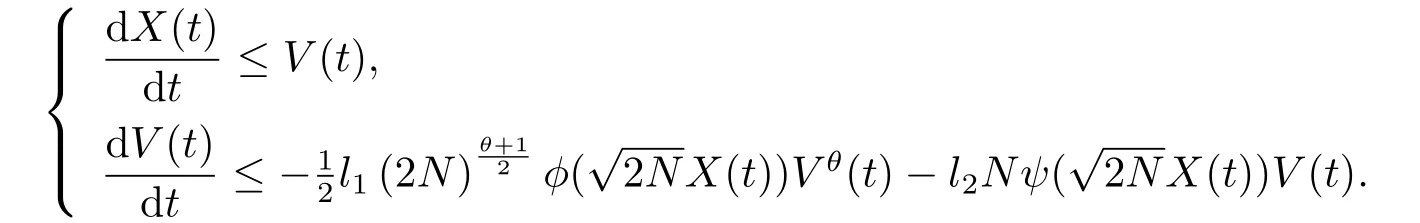
1)当l1=0，l2＞0时，即为文[2]中经典Cucker-Smale模型，则满足如下微分不等式组

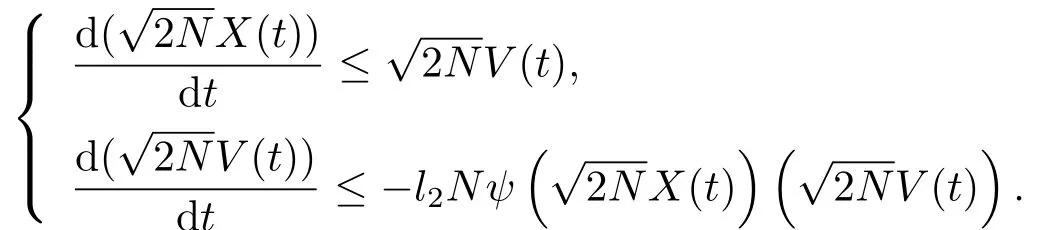
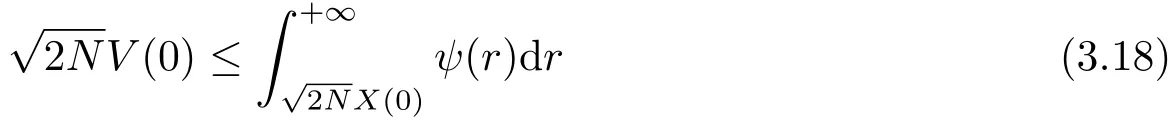
时，则有

故系统(3.2)形成集群，从而系统(1.2)形成集群.

2)当l2=0，l1＞0时，即为文[4]中模型，则满足如下微分不等式组

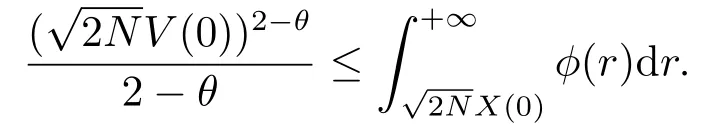
则有

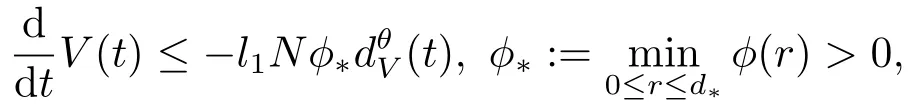
其中d*由如下式子给出

由引理2.3可知当t≥t1时，V(t)=0，其中t1满足

注意到当t≥t1时，V(t)=0，由(3.17)可知V(t)≤V(0)，因此

故系统(3.2)有限时间集群，从而系统(1.2)有限时间集群.

3)当l1＞0，l2＞0时，有

如果对(3.20)中第二个式子进行如下两种估计，第一种方式保留上式右边V(t)项，有

成立，即化成第一种情况，则系统形成集群.

第二种方式保留上式右边V θ(t)项，有

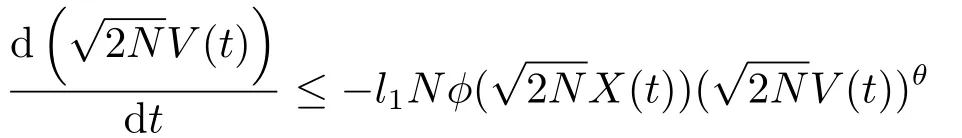
成立，即化成第二种情况，则系统有限时间集群.

综上两种估计，系统将有限时间集群.从上述证明可以看出，V(t)项对系统有限时间集群没有影响，下面我们讨论Lipschitz连续项对系统形成有限集群的时间大小的影响.

由引理2.6可知，若

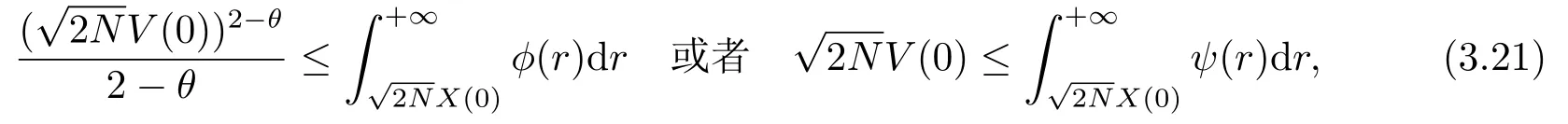
则当t≥t1时，有V(t)=0，这里

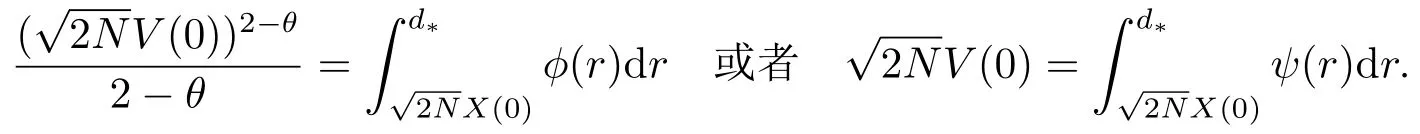
注意到当t≥t1时，V(t)=0，由(3.17)可知V(t)≤V(0)，因此有

故系统(3.2)有限时间集群，从而系统(1.2)有限时间集群.

注3.1在文[4]中，假设交流函数φ(·)有一个正的下界，在本文中我们运用Lyapunov函数方法改进文[4]中的结果，当φ(·)为单调递减的正连续函数时(不需要交流函数有正的下界)，系统将实现有限时间集群.

注3.2由上述第三种情况可知无论ψ(r)取何种函数时，不会影响系统实现有限时间集群，但会影响系统有限时间集群的时间大小，下面我们讨论这种影响，并给出时间大小的比较，在后面的仿真中可以验证其正确性.

为了给出Lipschitz连续项对系统有限时间集群时间的影响，则需要比较上述第二种和第三种情况有限时间集群时间的大小，即只需比较如下大小

这里的d*由第二种情况给出.由于

令

注3.3本文所讨论的模型与文[4]中模型比较:增加经典CS模型Lipschitz连续项，可以缩短系统实现有限时间集群的时间.经典的CS模型项不影响系统的有限时间集群，但影响着系统实现有限时间集群的时间大小.

注3.4对于系统(1.2)，取影响函数为φ(r)=ψ(r)=H，β＞0，当l1=0，l2＞0，即为文[1-2]中经典Cucker-Smale模型，系统渐进集群;当l1＞0，l2=0，即为文[4]中模型，系统有限时间集群.

4.数值仿真

在本节中，使用Matlab对如下系统进行了数值模拟.

其中aij(x)=φ(‖xi-xj‖)，bij(x)=ψ(‖xi-xj‖)，φ(·)，ψ(·)为单调递减的非负连续函数，l1，l2为非负数，且不能同时为0.

取粒子数N=40;空间维数d=2;系统中参数设置l1=l2=1，初值速度和位移分别为区间[-20，20]×[-30，20]和[-40，30]×[-40，10]上的随机数.下面分别对取不同的θ，影响函数φ(·)，ψ(·)进行数值模拟.

取θ=影响函数为φ(r)=(1+r2)－β1，ψ(r)=(1+r2)－β2;在初始条件相同的情况下，取不同的β1，β2进行仿真(如图4.1、4.2、4.3).

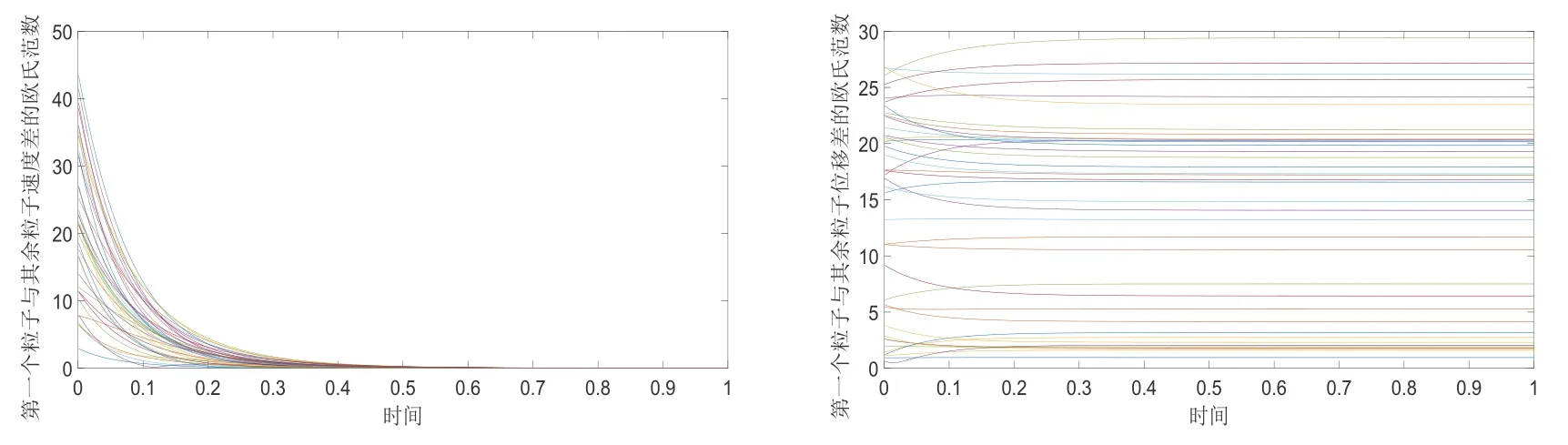
图4.2 取β1=2，β2=当0＜β2≤时，无论β1取何值，系统无条件渐近集群.左图为第一个粒子与其余粒子速度差的欧氏范数在1s内分布图，各粒子间速度差将趋于一致.右图为第一个粒子与其余粒子位移差的欧氏范数在1s内分布图，各粒子间位移差将保持有界.

图4.1 取系统无条件有限时间集群.左图为第一个粒子与其余粒子速度差的欧氏范数在1s内分布图，各粒子间速度差在有限时间内趋于一致.右图为第一个粒子与其余粒子位移差的欧氏范数在1s内分布图，各粒子间位移差在有限时间内将保持有界.

注4.1由上述三种不同形式(如图4.1，4.2，4.3)的仿真结果可以看出，β2对系统集群时间的影响更明显一些(如图4.1和图4.3).

图4.3 取β1=，β2=2，当0＜β1≤时，无论β2取何值，系统无条件有限时间集群.左图为第一个粒子与其余粒子速度差的欧氏范数在3s内分布图，各粒子间速度差在有限时间内趋于一致.右图为第一个粒子与其余粒子位移差的欧氏范数在3s内分布图，各粒子间位移差在有限时间内将保持有界.

上面对给定的θ，对不同的影响函数进行了数值仿真.由前面的第三种情况的证明可知，系统的Lipschitz连续项对系统的有限时间集群没有影响，只对系统实现有限时间集群的时间产生影响.下面对给定的交流函数，对不同的θ进行仿真.

选取交流函数为φ(r)=(1+r2)－β1，ψ(r)=(1+r2)－β2;当取初值相同，β1，β2固定时，分别对θ=0.3，0.4，0.5，0.6，0.7进行仿真，比较不同的θ对系统集群的影响.

图4.4 当时，在θ取不同参数下，左图为各粒子最大速度差在0.5s内分布图，右图为各粒子最大位移差在0.5s内分布图.

图4.5 当β2=2时，在θ取不同参数下，左图为各粒子最大速度差在6s内分布图，右图为各粒子最大位移差在6s内分布图.

5.结束语

本文主要讨论了一类带有非Lipschitz连续项与Lipschitz连续项混合型的Cucker-Smale模型有限时间集群的问题.研究结果表明，由(1.2)刻画的多粒子群，系统的集群性由非Lipschitz项决定，Lipschitz连续项不影响系统的有限时间集群，但影响系统有限时间集群的时间，在一定条件下，系统实现有限时间集群，当系统中取特定的参数时，包含了文[1-2，4]中的结果.