基于遗传优化径向基函数的梁板固有特性分析

荆栋，胡帅钊，邵明玉，马驰骋

(山东理工大学 交通与车辆工程学院,山东 淄博 255049)

板梁结构在机械制造、船舶重工和航空航天等工业领域广泛使用，因此开展薄壁结构的固有特性分析、获得结构的模态和固有频率对于工程结构设计具有重要的指导意义。目前，板梁自由振动分析中使用最广泛的数值方法是有限元法，然而有限元方法求解效率较低，通常需要大量计算网格才能满足计算精度要求。为了避免耗时繁琐的网格生成过程，最近发展起来的无网格方法在板梁结构的静态和瞬态分析中得到了越来越广泛的应用，如无单元Galerkin法、边界元法、径向基函数法(RBF)等[1]。

径向基函数法编程简单，在数据插值方面准确性高而且易于实现[2]。1990年，Kansa[3]全面深入地介绍了径向基函数法的相关概念，该方法有别于有限单元法，属于无网格数值方法，立足于通过数据插值建立偏微分方程数值解的对应关系。为了提高径向基函数法的准确性，Fasshauer等[4-5]使用具有平滑功能的多级方法来提高RBF方法的准确性，而Fedoseyev等[6]通过增加内部节点也达到了改善RBF方法准确性的目的。在薄壁板梁的振动分析方面:Chen等[7]通过在虚部基本解中引入RBF研究了圆形和矩形板的自由振动；Ferreira等[8-9]克服了RBF方法中的奇异解问题，使用预处理方法开展了复合材料层合板的自由振动分析，结合非对称径向基函数(RBF)配置方法对Timoshenko横梁和Mindlin板进行了自由振动分析；Misra[10]采用多二次径向基函数分析了各向同性板的自由振动，基于最小二乘误差范数的多元线性回归分析获得了固定和简单支撑矩形板的固有振动特性。

虽然国内关于径向基函数的研究开展的较晚，但是近年来在这一领域也取得了很多成果。王辉等[11]结合径向基函数法和梁的一般解提出了一种无网格配点解法，通过数值仿真算例验证了该算法的有效性和数值精度。项松等[12]研究了对称复合材料层合板的自由振动特性，发现逆复合二次径向基函数在对称复合材料层合板自由振动分析方面具有收敛性好及精度高等优点。王莉华等[13]采用径向基函数配点法研究了考虑剪切效应的梁板弯曲问题，联立径向基函数和最小二乘配点法离散方程，获得了较好的拟合结果。类似地，行凯歌[14]采用Hermite径向基函数配点法和最小二乘配点法分析层合板的弯曲问题，该方法计算稳定性高，适用于层合板大挠度弯曲问题的控制方程。李森[15]利用构造的单位分解径向基函数方法研究了2D弹性力学问题和压电问题。基于高阶剪切变形理论和逆复合二次径向基函数无网格配点法，祖福兴等[16]以强非线性梁为研究对象，提出了一种联合径向基函数-加权余量配点求解方法，针对具体边值条件，确定了相应的径向基函数插值表达式。崔攀等[17]在实验模态分析的基础上，构造径向基模型，并根据均方根误差准则提高模型预测精度，对比研究表明该模型在实际使用中具有较好的优势。

从文献回顾中可以发现，径向基函数的精度是限制该方法大范围应用的一个重要因素，近年来研究人员的工作重心主要集中在优化配点提高计算精度，但是效果并不明显。鉴于此，在前人工作的基础上，本文引入遗传优化算法，改进径向基函数以建立更加准确的力学模型。

1 数学模型

根据薄壁结构的弹性理论，在区间Ω上的静态板梁弯曲问题可以通过控制方程和边界条件方程来表示，即

(1)

式中：w是位移函数；L为线性微分算子；Ω和∂Ω分别表示结构的几何区域和边界；B和u分别表示边界方程的运算符和边界上的位移条件。与依赖于单元函数有限元方法相比，径向基函数法属于无网格算法，是一种基于节点的计算方法。基于径向基函数，位移函数w的径向基表达为

(2)

式中：c为形状函数；φ代表选定的径向基函数；r为坐标函数；N为网格点数量。函数近似处理中，选用合适的基函数可以有效提高近似效果。径向基函数具有多种选择，如表1所示。

表1 径向基函数

实践中发现，选择固定的形状参数c(均匀网格)可能是造成误差的主要原因，特别是在边界处理方面，引起的计算误差更加显著。因此，本文拟采用遗传算法优化径向基函数的形状参数c。

遗传算法尤其适合求解多目标组合优化问题，其求解速度快、计算精度高，而且程序开发成熟。在数学表达上，利用计算机仿真运算，将优化问题过程分解为生物进化中的染色体基因的交叉、变异等过程。实施过程中，首先需要将问题的解编码为一个二进制序列(也可以直接采用十进制编码)，所有的二进制序列在遗传算法中称为一个种群，然后计算目标函数、选择、交叉以及变异，模仿优胜劣汰的生物进化过程，经过多次迭代最终获得最优基因，也就是最优解。

2 板的固有特性分析

以板的固有特性分析为例，首先通过结构的静态分析和遗传优化分析，确定最佳的形状函数c，然后开展结构的固有特性分析。在实际工程中，可以设计简单的静态测量实验获取实际变形，然后通过遗传优化分析获取最优的c值，最后再利用c值进行结构的固有特性分析。

2.1 遗传优化分析

对于均质材料和恒定横截面的板，无量纲形式的均匀薄板的自由挠曲振动的控制方程如下：

(3)

(4)

考虑一个四面简支板，已知挠度具有如下解析形式：

(5)

其中系数Amn的具体形式为

(6)

采用径向基函数近似表示板的位移，即

(7)

结合公式(6)和公式(7)，定义目标函数

(8)

式中：‖·‖2表示L2范数(最小二乘数据拟合)；WRBF和Wexact分别代表板弯曲变形的径向基函数表达和精确解析表达。在实际问题中，结构边界的处理往往是比较复杂的，为了更好地解决边界处的微分条件，可以尝试Chebyshev网格。在本节的数值仿真中，同时考虑了均匀网格和Chebyshev网格两种网格模式，如图1所示。

(a)均匀网络 (b)Chebyshev网格

在研究中，我们只对形状参数c开展遗传优化分析，遗传迭代结果如图2所示。从图2可以看出，使用遗传算法可以迅速得到最优的形状函数值。仿真中以迭代次数作为程序运行截止条件，通过MATLAB软件编写了遗传优化算法，迭代截止次数设置为100。

图2 遗传迭代优化过程(11＊11)

采用均匀网格和Chebyshev网格计算得到的系统第一阶振型如图3所示，使用遗传优化径向基函数法得到的模态和解析解对比一致，说明了该优化方法的有效性。

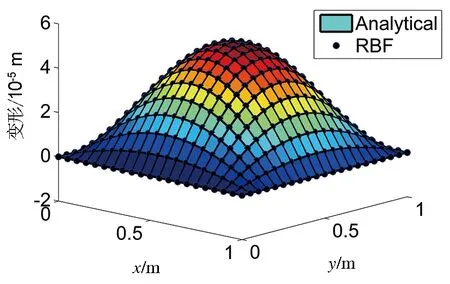
(a)均匀网格

2.2 固有特性分析

无量纲化薄板振动特征方程可以表示为[10]

λ4w(x,y)，

(9)

式中：a为板的长度；R为板长度a和板宽度b的比值。此时特征值λ和结构的固有频率ω满足

(10)

将公式(7)带入方程(9)得到

(11)

将公式(11)改写成矩阵形式，并且考虑四面简支处位移为零，得到如下公式：

(12)

其中A和B的表达式分别为

式中φij(x,y)=φ((xj-xi)2+(yj-yi)2+r2)，进一步我们可以将公式(13)写为矩阵形式

(14)

在求解特征方程(14)时，可以使用如下的替换公式：

A*w=λw，

(15)

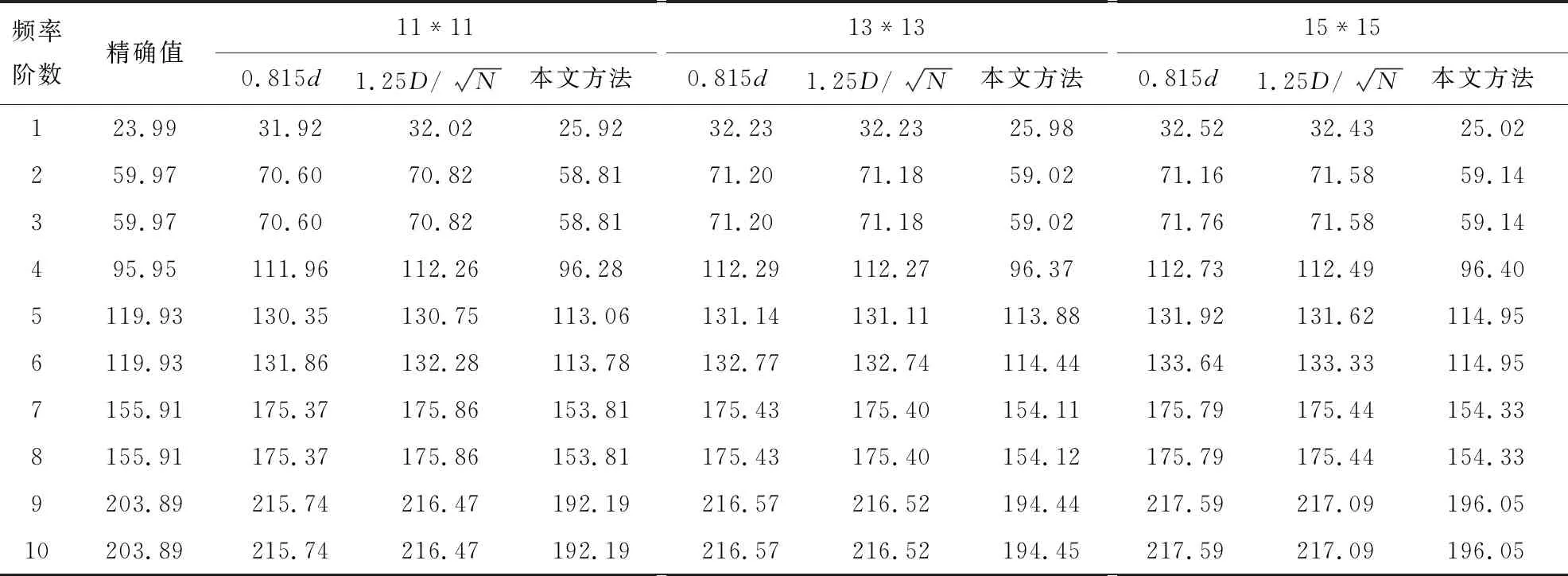
表2 四面简支板的固有频率

采用Chebyshev网格可以有效改善边界处导数精度，因而显著提高计算精度。表3和表4给出了使用均匀网格和Chebyshev网格时，四面简支板的前十阶固有频率值。对比两种网格方法可以发现，使用Chebyshev网格时，计算精度更高，第一阶频率的计算误差最大是3.5%，第十阶频率的计算误差为2.8%。图4给出了四边简支板的前九阶振型，与解析模态解是完全一致的。

图4 四面简支板的前九阶模态

表3 四面简支板的固有频率(均匀网格)

表4 四面简支板的固有频率(Chebyshev网格)

3 梁的固有特性分析

3.1 梁的模态分析

与板的固有特性分析类似，首先通过静态分析和遗传优化径向基函数法得到优化后的形状参数，然后进行两端简支梁的固有特性分析。对于受均布载荷作用的梁结构，其运动微分方程为

(16)

式中：EI为抗弯刚度；ρ和A分别表示密度和梁的横截面面积。对于准静态分析，忽略惯性项，可以得到梁结构的变形方程为

(17)

根据材料力学知识可知，受均布载荷作用的两端简支梁的变形为

(18)

图5 梁及Chebyshev网格图

利用径向基函数表达和解析解(18)设计目标函数，用于遗传优化分析，即

(19)

式中WRBF和Wexact分别代表梁弯曲变形的径向基函数表达和精确解析表达。仿真中通过MATLAB软件编写了遗传优化算法，迭代截止次数设置为100。针对N=21和N=31两种网格数目进行了遗传优化分析，遗传迭代结果如图6所示。可以看出，使用遗传算法可以迅速得到最优的形状函数值。

(a)N=21适应度

利用基于GA的最佳形状参数的径向基函数说明了简单支撑梁的模态形状，最佳形状参数使径向基函数更加精确。将优化后的形状参数c带入弯曲变形的挠度表达式，解析结果和RBF求解结果如图7所示。对比这两种情况可以发现，即使采用较为稀疏的网格，径向基函数近似表达和解析表达也几乎一致，说明了优化的有效性。

图7 两端简支梁的变形

3.2 梁的模态分析

利用优化结果和径向基函数表达，进一步开展了梁结构的固有特性分析。将计算得到的形状函数带入到梁的特征方程中，便可以求得固有频率值和对应的振型。前五阶模态如图8所示。从图8中可以看出，网格数目越多，径向函数近似表达越精确，因此得到的模态曲线越光滑。

图8 两端简支梁的前五阶模态

表5—表7列出了采用不同径向基函数时，两端简支梁结构的固有频率值。从列出的频率中可以发现，使用具有最佳形状参数的径向基函数，可以获得比较精确的固有频率值，从而显示了遗传优化径向基函数的有效性。可以看出，网格数量对于结果的影响比较小，也就是说采用遗传优化径向基函数法，使用较少的网格点即可以满足计算精度要求。对比表5—表7也可以发现，对于梁结构来说，使用IMQ函数比高斯分布函数可以取得更加准确的结果，因此在梁结构的固有特性分析中，建议采用IMQ径向基函数。

表5 两端简支梁的前五阶固有频率 (MQ函数)

表6 两端简支梁的前五阶固有频率 (IMQ函数)

表7 四面简支板的前五阶固有频率 (高斯函数)

4 结论

对薄壁梁和板的固有特性进行了分析，基于遗传算法和径向基函数法求解薄壁板梁结构的固有频率和模态,采用遗传算法对RBF的形状参数进行了优化。使用优化的形状参数后，可获得更好的结果，且本文结果可以推广到悬臂梁、两端简支板等结构的固有特性分析，也可以用于复合材料薄壁结构的动力学设计。具体结论如下：

(1)使用遗传算法可以快速获得优化的形状参数，提高径向基函数的精度。通过比较多二次、逆多二次和高斯插值径向基函数法得到的数值结果，显示出形状参数c的良好值。

(2)当网格数量远大于模态求解阶数时，增加网格数量对结果的影响比较小。

(3)使用Chebyshev网格计算的结果要好于使用均匀网格计算的结果，对于板梁结构来说，采用逆多二项式径向基函数可以得到较好的结果。