随机交叉-自学策略改进的教与学优化算法

黎延海，雍龙泉,2，拓守恒

（1. 陕西理工大学 数学与计算机科学学院，陕西 汉中 723001; 2. 陕西省工业自动化重点实验室，陕西 汉中723001; 3. 西安邮电大学 计算机学院，陕西 西安 710121）

教与学优化算法(teaching-learning-based optimization，TLBO) 是Rao等[1]于2011年提出的一种模拟教师教学和学生相互学习的群体智能优化算法。该算法因参数设置少、容易实现、寻优性能好，受到了众多研究者的关注，在函数优化[2]、工程参数优化[3]、投资组合优化[4]和多目标优化[5-6]等问题上得到了广泛的应用。

TLBO算法作为一种群智能优化算法，在求解高维多模态复杂优化问题时也容易陷入局部最优，算法的收敛速度和精度都不够理想，为此，许多研究者在近几年相继提出了一些改进的TLBO算法。Ouyang等[7]为平衡全局与局部搜索效率，在“学阶段”增加了全局交叉策略，提出了全局交叉的TLBO算法(teaching-learning-based optimizatio with global crossover,TLBO-GC)；Chen等[8]设计了局部学习和自学习方法来提高TLBO的搜索能力，提出了一种改进的TLBO算法(improved teaching-learning-based optimization,ITLBO)；Zou等[9]利用其他同学的学习经验，使用两种随机概率来确定学习者在不同阶段的学习方法，提出了一种改进的TLBO算法(improved teaching-learning-based optimization with learning experience, LETLBO)；王培崇等[10]采用小世界网络作为种群的空间结构关系，提出了具有小世界领域结构的TLBO算法(small world neighborhood TLBO, S-TLBO)；毕晓君等[11]在“学阶段”融合差分进化算法变异策略，提出了基于混合学习策略的教与学优化算法(TLBO based on hybrid learning strategies and disturbance, DSTLBO)；Ji等[12]受历史种群概念的启发，在标准TLBO算法中引入了自反馈学习阶段和变异交叉阶段，提出了一种TLBO算法的变体(improved version of TLBO, ITLBO)；Yu等[13]将精英学习策略和多样性学习方法引入到教师阶段和学习者阶段，学习者可以根据自身的特点自适应地选择不同的学习阶段，提出了一种自适应的TLBO算法(self-adaptive TLBO, SATLBO)；Niu等[14]对种群中每个个体采用不同的更新机制，提出了一种修正的TLBO算法(actual teaching learning situation TLBO, ATLS)；SHUKLA等[15]在标准TLBO算法中引入邻近学习和差分突变策略，提出了邻近学习策略的TLBO算法(neighbor based TLBO, NTLBO)；柳缔西子等[16]利用权重学习得到的个体来指引种群的进化，使用Logistics 混沌搜索策略来提高其全局搜索能力，提出了基于混沌搜索和权重学习的教与学优化算法(TLBO based on chaotic search and weighted learning,TLBO-CSWL)；何杰光等[17]在原有的个体更新公式上加入更新个体局部维度的操作，提出了基于个体局部维度改进的教与学优化算法(local-dimension-improved TLBO, LdimTLBO)；Tsai[18]将交叉频率引入TLBO中，以防止算法过早收敛，提出了受限的教与学优化算法(confined TLBO with variable search strategies, CTLBO)。这些TLBO的改进算法在一定程度上提高了算法的优化性能，降低了算法陷入局部最优的可能，但文献[19]揭示标准TLBO算法在“教”阶段存在固有的起源偏倚，对原点最优问题(以坐标原点为最优解的问题)有着原始的偏好，但对非原点最优问题(最优解不在坐标原点的问题)的优化效果则不太理想，现有的改进TLBO算法也没能很好地解决这类问题。

为此，本文在对标准TLBO算法的“教阶段”和“学阶段”的空间扰动进行几何分析解释的基础上，提出了一种基于随机交叉-自学策略的教与学优化算法(teaching and learning optimization al-gorithm based on random crossover-self-studystrategy, CSTLBO)。算法使用各分量取值 [-1,1]的随机向量替换了标准TLBO算法中各分量取值[0,1] 的随机向量，通过引入随机交叉策略和“自学”策略，增加种群的多样性，提高算法的全局搜索能力。使用了20个Benchmark测试函数进行仿真实验，并与6种TLBO的改进算法(TLBO-GC[7]、ITLBO[8]、DSTLBO[11]、ATLS[14]、NTLBO[15]、TLBO-C SWL[16])进行了比较，检验了所提算法的性能。

1 教与学优化算法

1.1 优化问题的模型

本文研究的优化问题的具体模型为：

式中：X 为决策向量；S 表示搜索空间；xiL和 xiU分别表示第 i 个决策变量 xi在搜索空间的上界和下界 ；D 是搜索空间的维数；f 为目标函数。

1.2 标准的教与学优化算法

标准TLBO算法是一种模仿整个课堂教学过程的高效优化方法，通过模拟老师给班级学生的教学过程及班级中学员之间的交流学习过程，来提高整个班级的成绩。主要包括两个阶段：“教阶段”和“学阶段”，其基本步骤如下：

1)初始化。随机初始化 NP 位学员(即个体) Xj=(x1j,x2j,···,xDj)，j=1,2,···,NP 。其中， N P 表示班级中的学员数(即种群的规模)，D 表示学习的科目数(即待优化问题的维数)。

2)“教阶段”。选取班级中成绩最优(即适应度值最小)的学员作为老师，记做 Xteacher，每个学员根据教师和全体学员平均水平的差异性(difference)来进行学习，具体如下：

式中：Xjold、Xjnew分别表示第 j 位学员 Xj在教学前、后的知识水平；r=(r1,r2,···,rD) 表示学习步长，ri为 [0,1] 间的随机数；符号 ⊗ 表示直积运算；TF=round[1+rand(0,1)] 表示教学因子，取值为表示班级全体学员的平均知识水平。

“教阶段”完成后，评估学员Xj的学习成绩(即适应度值f(Xj) )，如果，则进行更新，即否则不更新。

3)“学阶段”。学员之间进行相互交流，通过向其他同学学习，来提升自身的水平。从班级中随机抽取一个学员Kk，k是[1,NP]中的一个随机整数，k≠j，学员Xj(与其进行)交流学(习，)具体(如)下：

4)如果满足终止条件(达到最大评估次数或最大迭代次数)，则优化结束并输出最优个体Xbest，否则转至2)继续。

2.1 标准TLBO算法的几何解释

为了更好地理解TLBO的工作原理，以二维空间为例，采用几何分析的方法来解释算法在“教阶段”和“学阶段”的空间扰动状况。

文献[19]指出式(2)和(3)中的r本质上是一个各分量都取值于[0,1]的D维随机向量，考虑到由随机参数所引起的扰动的极限情形，容易观察出“教阶段”和“学阶段”的空间扰动情形。由于r中的每个元素都是取值于[0,1]的随机数，所以r对difference的影响实际是一个尺度上的缩放，即difference可以为图1(b)、(c)方框内的任意向量。图1(a)给出了TF(取1或2)的两种情况下difference的向量表示；图1(b)描述了“教阶段”，应用于Xj的两个可能的扰动框，从概率角度描述了应用于Xj每一个可能的扰动；图1(c)描述了“学阶段”，应用于Xj的两种可能的扰动框。

图 1 扰动分析的几何解释Fig. 1 Geometric interpretation of disturbance analysis

2.2 随机向量的扰动分析

类似于2.1节的分析，如果将式(2)和式(3)中各分量取值于[0,1]的随机向量替换为各分量取值于[-1,1]的随机向量，则应用于Xj的扰动范围将会扩大，“教阶段”的搜索扰动范围会变为原来的4倍，而“学阶段”的扰动范围将变为原来的两倍，这样能增大算法跳出局部最优的概率，在一定程度上改善算法“早熟”收敛的状况，提高全局搜索能力。

图2(a)、(b)分别描述了在“教阶段”和“学阶段”，使用各分量取值于[-1,1]的随机向量后，应用于Xj的可能的扰动范围。

图 2 扰动分析的几何解释(ri∈[-1,1])Fig. 2 Geometric interpretation of disturbance analysis(ri∈[-1,1])

2.3 随机扰动的实验分析

为检验上述对使用不同取值范围的随机数所产生的扰动状况的分析，将标准TLBO算法和TLBO1(r为各分量取值于 [-1,1] 的随机向量)在6 个标准测试函数上进行仿真测试，其中f1～f3是典型的原点最优的多峰问题，f4～f6是对它们进行了Shift操作(非原点最优)。设置维度D=30，种群大小 N P=10，评价次数为150 000次。表1统计了30次独立运行得到的最优目标值的平均值、标准差及运行时间，图3给出6个函数的收敛曲线。

表 1 30次实验统计结果Table 1 Thirty times optimization statistical results

图 3 测试函数f1～f6的收敛曲线图Fig. 3 Convergence plot of benchmark function f1～f6

从表1和图3可以看出，对原点最优问题，标准TLBO算法所得解的精度更高，时间更短，但对非原点最优问题，TLBO1算法的求解精度和时间则更优。由于标准TLBO算法的“教”阶段存在固有的原点偏倚，允许收敛的种群继续沿着原点的方向搜索更好的解决方案，从而对原点最优问题能取得更好的优化效果。对非原点最优问题，标准TLBO算法在种群收敛到局部最优时，要么继续利用局部最优信息，要么沿着原点方向继续探索，由于最优解在原点以外的点上，沿原点方向的搜索几乎毫无意义，所以无法进一步获得高精度的解；而采用各分量取值于 [-1,1]的随机向量，使得搜索范围成倍扩大，算法跳出局部最优的能力得到提高，获得最优解的概率变大，随着迭代的 进行，能取得更好的优化效果。

3 基于随机交叉-自学策略的教与学优化算法

标准TLBO算法中，由于教师和学习对象都属于现有种群，所以无论是“教阶段”还是“学阶段”的操作都是在当前位置的有限范围内进行搜索，学习者都依据现有种群的经验来提高自己的成绩，使得算法具有良好的开发性能，而跳出局部最优的能力不足。为增强算法的全局搜索能力，使迭代过程中算法的探索与开发过程得到平衡，对“教”和“学”阶段进行改进，并使用随机交叉策略和“自学”策略，来提高算法对复杂多模态问题的优化性能。

3.1 “教阶段”的改进

当班级中学生成绩差异较大时，最差成绩往往会拉低班级的平均水平，如果教学过程中重点加强对最差生的关注，使其成绩得到大幅度提高，缩小与班级其他同学间的差距，则可以加快班级整体水平的提升。故用班级中的成绩最差者Xworst替 换班级平均水平 Xmean，即

式 中r1为各分量取值于 [- 1,1] 的随机向量。

3.2 “学阶段”的改进

其中，r2为各分量取值于 [-1,1] 的随机向量，k 是[1,NP] 中的一个随机整数，k≠j，t 为当前迭代次数，Tmax为最大迭代次数。在迭代初期，t 较小，(1-t/Tmax) 的值较大，学生间的相互讨论更多，算法更加注重随机性学习，能够维持种群多样性，增大有效搜索范围；随着迭代的进行，t 逐渐增大，(t/Tmax) 越来越大，学生会更多地向老师求教，逐渐侧 重于有向性学习，使算法的局部搜索能力增强。

3 .3 随机交叉-自学策略

3.3.1 随机交叉策略

学生经过“教”阶段后，各自的成绩会得到一定程度的提升，但彼此间的差距也会缩小，即种群的多样性降低，而通过集体讨论交流，每位学生都可以在不同科目上随机地向班级中不同的同学求教，并达到该同学在此科目上的水平，这实际上就是种群间的一种随机交叉过程，具体为

i=1,2,···,D,j=1,2,···,NP，k 是 [1,NP] 中的一个不同于 j 的随机整数，r and 为 [0,1] 间的随机数。这里使用一种随机概率来确定学习者与不同学习对象间的交流程度，通过进行种群间的随机交叉，能够维 持种群的多样性，提高算法跳出局部最优的能力。

3.3.2 “自学”策略

实际学习过程中，部分学生在学习之余，也会根据自己当前的学习状况，挑选部分课程进行“自学”，发掘新的知识，从而提升自己的学业水平。具体如下：对第 i 门课程，产生一个 [0,1] 间的随机数 r and，来用于选择不同的“自学”方式。

i=1,2,···,D,j=1,2,···,NP 。其中， S DR(selfdevelopment rate, SDR)为自我拓展率，λ 表示自学步长，λmax、λmin分别为最大、最小步长。

磁性纤维素对亚甲基蓝的吸附过程受吸附反应温度、溶液pH值和吸附时间的影响，吸附的最佳实验条件是反应温度293 K；溶液pH值为7；吸附时间120 min。磁性纤维素对亚甲基蓝的吸附动力学特征用准二级动力学模型拟合较好；等温吸附以Langmuir拟合最佳，由此可得磁性纤维素对亚甲基蓝最大理论吸附容量为123.15 mg·g-1。

对每一科目，学生会根据自己当前的知识水平随机进行自我调整，提高学习效率，自学步长随迭代的进行由 λmax逐步动态缩小为 λmin。搜索前期，步长值较大，算法具有强的空间扰动能力，有助于探索新的未知区域；随着迭代的进行，步长值逐渐缩小，使得对当前解的扰动幅度变小，有利于提高解的精度，这样一种动态调整过程能有效平衡算法在搜索过程中的空间扰动能力和局部寻优能力。同时，以概率 S DR 在搜索空间进行随机搜寻，进行自我拓展学习，可以增加算法的全局搜索能力。大量数值实验测试表明，自我拓展率取值不宜过大，当SD R∈[0.01,0.1] 时，算法会有较好的性能。

3.4 CSTLBO算法的流程

CSTLBO算法的具体流程如图4所示。

图 4 CSTLBO算法流程Fig. 4 Flow chart of CSTLBO algorithm

每次迭代过程中，对每位学生而言，依据选择概率 SP来选择“学”和“自学”两种学习方式中的一种执行，具体如下：

随迭代的进行，SP 的值从 S Pmax逐渐减小到SPmin，表明在迭代初期，同学之间的信息交流比较多，随着学习的深入，当学生的水平都得到较大提 升后，会更多地倾向于进行自我探索学习。

4 实验仿真测试

4.1 测试函数与参数设置

为检验CSTLBO算法在连续优化问题中的性能，将其与6种TLBO的改进算法(ATLS、

NTLBO、TLBO-GC、ITLBO、TLBO-CSWL、DSTLBO)在20个复杂Benchmark函数上进行测试比较。将函数F1，F3～F4称为原点最优问题(它们在原点处得到了最优值)，其余的函数称为非原点最优问题，其中一些是通过对原点最优问题进行移位和旋转得到的，移位函数取自CEC 2008，移位和旋转函数取自CEC 2017。

F1为Ackley Function；F2为Michalewics Function；F3为Rastrigin Function；F4为Griewank Function；F5为Schwefel 2.26 Function；F6为Weierstrass Function；F7为FastFractal ‘DoubleDip’ Function；F8为Sphere Shift Function；F9为Ackley Shift Function；F10为Griewank Shift Function；F11为Rastrigin Shift Function；F12为Rosebrock shift Function；F13为Schaffer Shift Function；F14为Bohachevsky Shift Function；F15为Shifted and Rotated Rastrigin’s Function；F16为Shifted and Rotated Expanded Scaffer’sF6Function；F17为Shifted and Rotated Lunacek Bi_Rastrigin Function；F18为Shifted and Rotated Non-Continuous Rastrigin’s Function；F19为Shifted and Rotated Levy Function；F20为Shifted and Rotated Schwefel’s Function.

本文测试的环境为：戴尔PC机Intel Core(TM)i7-4790 3.6 GHz CPU，8 GB内存；Window10操作系统；MATLAB R2014b软件。为保证测试的公平，各种算法采用相同的适应度函数评价次数：对F1～F14，评价次数MaxFEs=5 000×D；对F15～F20，MaxFEs=10 000×D，其中D为维数。比较算法的参数设置均参考于原文献，本文算法的参数设置为： N P=20， S Pmax=0.6， S Pmin=0.2，S DR=0.02，λmax=(xU-xL)/10，λmin=(xU-xL)/(1015)。

4.2 实验结果与分析

为避免偶然因素的影响，所有算法在D=100时都独立运行了30次，表2记录了各种算法在20个测试函数上30次独立实验的统计结果，对F1～F14，记录了最优目标值的平均值和标准差，对F15～F20，记录了最优误差的平均值和标准差。为检验本文算法与比较算法之间的差异性，进行了显著性水平为0.05的Wilcoxon秩和检验，“+”、“-”、“≈”分别表示比较算法与本文算法的成绩相比是好、差和相当。

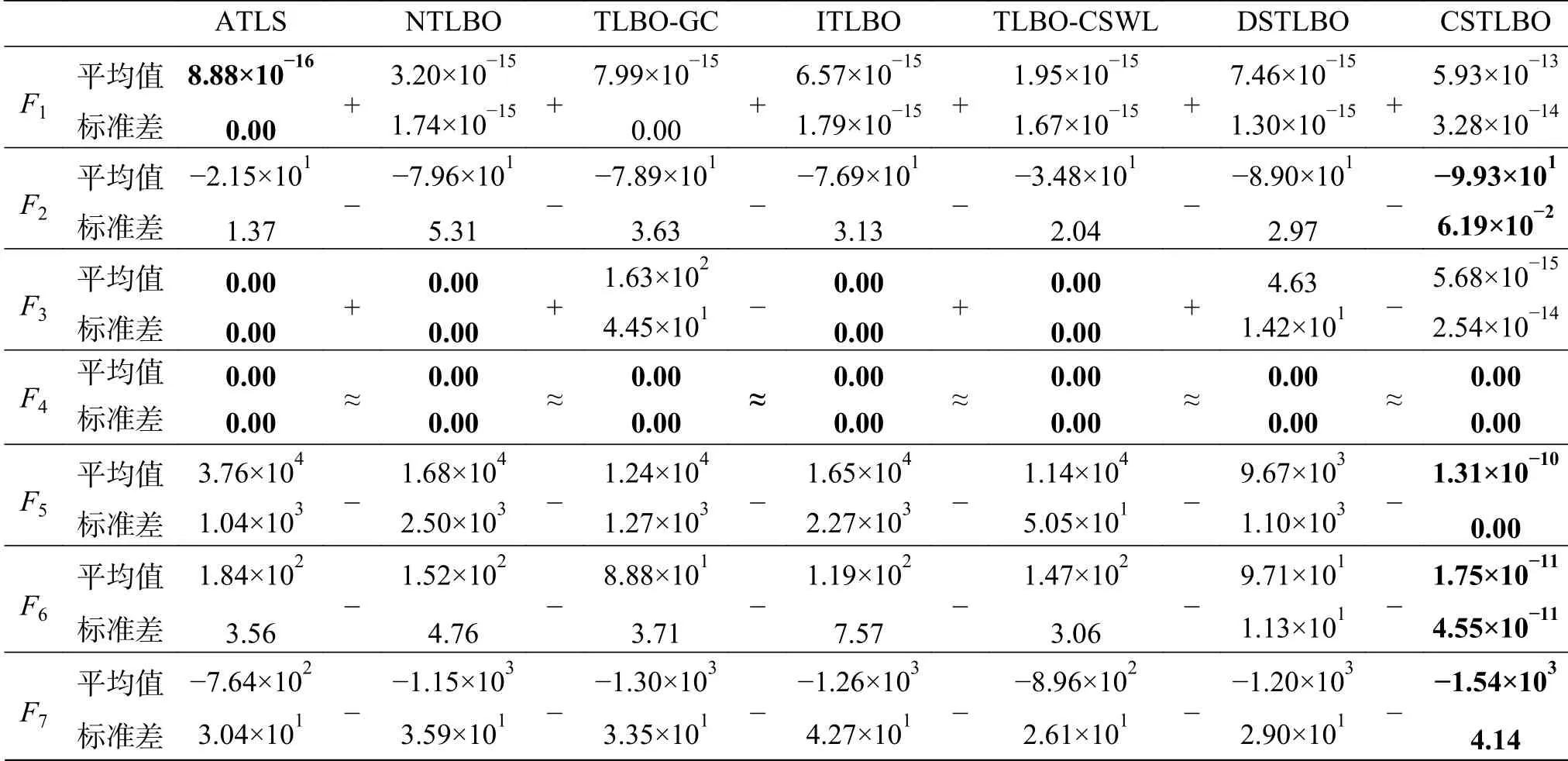
表 2 算法30次独立测试结果(D=100)Table 2 Thirty times optimization results of the algorithm(D=100)

续表 2

从表2可以看出，所有比较算法在F1这个原点最优问题上的收敛精度优于本文算法，在F4上所有算法都能达到理论最优值，除F20外，本文算法在余下的17个测试函数上的平均值和方差都优于比较算法，说明所提算法对非原点最优问题的优化能力较强，效果良好。从Wilcoxon符号秩检验的结果来看，比较算法最多在4个问题上优于或相当于本文算法，而在其余测试问题上都明显差于本文算法。

为进一步分析实验结果，图5～6给出了30次独立运行的平均最优目标值收敛曲线(D=100维)，图7～8给出了30次独立运行的最优目标值分布盒图(D=100维)。

图 5 测试函数F11的收敛性曲线Fig. 5 Convergence plot of benchmark function F11

图 6 测试函数F19的收敛性曲线Fig. 6 Convergence plot of benchmark function F19

图 7 测试函数F11的最优目标值分布盒图Fig. 7 Boxplot of the optimal value distribution of benchmark function F11

图 8 测试函数F19的最优目标值分布盒图Fig. 8 Boxplot of the optimal value distribution of benchmark function F19

从收敛曲线图不难看出，本文算法对两个复杂优化函数(Rastrigin Shift Function、Shifted and Rotated Levy Function)的收敛曲线呈逐渐下降趋势，收敛效果明显优于其他比较算法，说明本文算法的全局搜索能力较强，不易陷入局部最优。

从统计盒图可以看出，本文算法30次独立实验所得的最优值的分布基本呈一条直线，差距很小，说明本文算法具有良好的稳定性。

4.3 随机交叉策略的有效性分析

为检验本文所使用的随机交叉策略的有效性，选取了复杂的非原点最优问题Weierstrass Function进行了测试，函数Weierstrass Function具有多个极小值点，算法很容易陷入局部最优的状况。设置维数D=30 , 种群大小 N P=20, 最大评价次数MaxFEs=150 000，对搜索过程中产生的所有搜索点和每代的最优搜索点进行了跟踪记录，用于观察算法的搜索过程。图9描绘了搜索点(取30维中的2维绘制)的分布图。

图 9 搜索点分布Fig. 9 Search point distribution

从图9可以看出，未使用随机交叉策略的搜索过程中，种群在多个局部极值处都有聚集，使得在相同评价次数下，无法进行有效的开发，所得解的精度不高；而使用了随机交叉策略的搜索种群的分布很均匀，没有发生陷入局部最优的现象，大多数搜索点都聚集于最优解附近，更多地来进行局部开发，说明随机交叉策略能使算法有效 地跳出局部最优，增强算法的全局搜索能力。

4.4 CSTLBO算法的种群多样性分析

为进一步研究CSTLBO算法的收敛过程，以4个复杂非原点最优测试函数(Schwefel 2.26 Function、Ackley Shift Function、Griewank Shift Function、Rastrigin Shift Function)为例进行实验(取维数D=100)，在搜索过程中跟踪记录了算法种群多样性的变化，如图10所示。种群多样性[20]定义如下：

图 10 4个复杂非原点最优测试函数的种群多样性曲线Fig. 10 Population diversity curves of four complex non- origin optimal benchmark function

从图10可以看出，标准TLBO 算法在搜索初期多样性明显快速下降，然后在小范围内波动，前后期变化不是特别明显，使得种群个体难以聚集到全局最优解，因此求解精度不高；CSTLBO 算法在迭代初期，具有较高的种群多样性，有利于进行全局探索，随着迭代的进行，种群多样性保持着持续下降的趋势，种群逐渐向全局最优解聚集，有利于进行局部开发，从而能获得高精度的全局解。

5 结束语

为提高对非原点最优问题的优化能力，本文提出了一种基于随机交叉-自学策略的教与学优化算法—CSTLBO。算法使用几何方法分析了标准TLBO算法在“教”和“学”阶段的扰动状况，改进了 “教”和“学”阶段，并引入了随机交叉策略和“自学”策略来提高算法的全局搜索能力。仿真测试的统计结果表明，所提算法求解精度高，稳定性好，能对较多的非原点最优问题取得良好的优化效果，尤其是对进行了移位操作的复杂问题。但对同时进行了移位和旋转操作的问题，优化结果虽优于比较算法，但在求解精度上仍有提升空间，在后续研究中，可以进一步研究改进，同时也可以将该算法应用到实际的工程优化问题，检验其具体实用性。