基于张量链分解的低秩张量补全研究

豆 蔻，吴云韬*，黄龙庭，陈 里

1.武汉工程大学计算机科学与工程学院，湖北 武汉430205；2.武汉理工大学信息学院，湖北 武汉430070；3.武汉工程大学邮电与信息工程学院，湖北 武汉430074

张量作为向量和矩阵的高阶扩展，同时能够保留数据的高维结构，适合用来表示自然中具有多维特征的数据。张量已经在许多领域得到了广泛的应用，包括信号处理［1-2］、计算机视觉［3-4］、神经科学［5］和机器学习［6］。然而实际采集到的高维数据通常是遭到破坏或有部分缺失的，对于这种情况，可以根据已观测到的部分数据来恢复其缺失部分，这就是张量补全研究。本文研究的低秩张量补全问题是通过张量分解获得的潜在低秩表达与数据低秩的特性，利用数据空间中数据的低秩关联结构更有效地预测缺失部分。

CANDECOMP/PARAFAC分解［7］和Tucker分解［8］是经典的张量分解方法，已经有许多基于它们的张量补全算法，例如CP分解加权法（CP-weighted optimization，CP-WOPT）［9］，完全贝叶斯处理（fully Bayesian CP factorization，FBCP）［10］以及张量同时分解和补全方法（simultaneous tensor decomposition and completion，STDC）［11］。但是，由于经典张量分解模型的局限性，仅在低维张量补全时才能达到较高的精度，并且容易因为维度太大参数过多而遭受“维度诅咒”。近来，已经提出了一种基于矩阵乘积状态（matrix product state，MPS）模型的张量链分解［12］，张量链分解能够将高阶张量分解成一组三阶张量，具有很高的数据压缩能力和计算效率，本文将基于张量链分解研究低秩张量补全问题。

目前广泛应用的低秩张量框架是将张量每个模展开矩阵的秩作为优化目标，通过求解秩加权和最小化问题来低秩近似原始张量。由于张量低n-秩最小化模型是一个多项式的非确定性问题（non-deterministic polynomial，NP），需要对秩 函数进行凸松弛，通常的做法是转换成独立的模展开矩阵的核范数求解，这样每次迭代都需要进行大量的奇异值分解（singular value decomposition，SVD）计算。尽管最近已经提出了许多基于张量链分解的张量补全方法，但是与它们对原始数据施加低秩约束不同，受Tucker分解核心张量核范数［13］的启发，本文在张量链核心张量上引入最小化约束，这可以将大规模张量核范数问题转换为小型核心张量核范数问题来解决，基于张量链分解的核心张量来解决低秩张量补全问题，并且给出了具体算法流程，最后运用交替方向乘子法（alternating direction of method of multipliers，ADMM）［14］求解，使其在迭代过程中具有稳定性能并且计算高效。

1 张量链分解

采用通用的张量表示方法［15］，标量用大小写字母表示，例如x，X，矢量和向量用加粗的小写字母表示，例如x，矩阵由加粗的大写字母表示，例如X，张量用手写体表示，例如X。设I1,I2,...,IN表示各维度大小，张量X∈ ℝI1×I2×…×IN表示一个大小为I1×I2×…×IN的N阶张量。X(1),X(2),…,X(N)表示张量序列，其中X(n)表示序列中的第n个张量。张量个元 素 可 以 表 示 为xi1i2…iN或 者 X(i1,i2,…,iN)。表示张量X的模式-n矩阵展开，其反向操作是fold(n)(X)，表示将[X](n)恢复成张量X。

另外给出张量内积和Frobenius范数定义，两个相同大小张量X，Y的内积定义如下：

张量X的Frobenius范数定义如下：

张量链分解［12］将高阶张量分解为一组三阶张量，这有助于从原始的高阶张量获得低阶核心张量。张量X∈ℝI1×I2×…×IN的张量链分解形式可以表示为：

核心张量G(n)是大小为Rn−1×In×Rn的三阶张量，中间阶大小In为原始张量对应阶的维数，剩余两阶的维数称为张量链分解秩。序列(R0,R1,…,RN)定义为张量链分解表达的秩，为了最终乘积是一个标量，还需要秩约束为R0=RN=1的边界条件。此外对张量中每个元素还有如下分解表达式：

其中G(n)(in)∈ℝRn−1×Rn是核心张量的模-2切片矩阵，也可以定义为G(n)(:,in,:)。本文中用运算符Ψ表示核心张量生成近似张量的的过程，即X=Ψ[G(n)]。

2 张量链核心张量核范数最小化方法

根据核心张量与原始张量之间的维度大小对应关系，可以得出张量的秩受到其核心张量的秩的约束，意味着如果对核心张量施加低秩约束的同时也对张量自身进行了低秩约束，考虑到核心张量较之原始张量有更低的维度，本算法选择直接把核心张量的秩函数作为优化目标，因此提出基于张量链核心张量的低秩张量补全问题，表达式为：

其中X表示经过补全算法得到低秩张量，Ω表示所有已知元素的集合，T表示张量中可以观测到的部分，Ψ[G(n)]表示核心张量生成近似张量的运算。

然而上述秩函数问题是一个NP难问题，需要用核心张量的核范数代替秩正则化进行凸松弛。根据张量核范数的定义，又考虑到每个三阶的核心张量分别有3种模展开方式，结合这3种模展开矩阵，可以得到核心张量的核范数定义如下：

其中||·||∗表示核范数计算，即矩阵所有奇异值 的 和并且αn＞0表示各模式矩阵核范数的加权。结合核心张量核范数的定义以及式（5）的补全模型，将条件中的等式约束转换为用来约束恢复的张量X与核心张量生成的张量Ψ[G(n)]的近似性，λ是一个用来平衡低秩约束项与近似约束项的参数，由此得到式（5）的松弛模型，如式（7）所示：

式（7）称为基于张量链分解的核心张量核范数的低秩张量补全模型（low-rank tensor-train core tensor nuclear norm minimization，LTTCTNNm），接下来展示算法的具体求解方法。

由于优化问题中的变量是相互依赖的，引入辅助张量Mn,i,n=1,…,N,i=1,2,3来使变量分离，从而转化为如式（8）的问题：

通过将等式约束合并到拉格朗日函数中，得到式（8）的增广拉格朗日函数为：

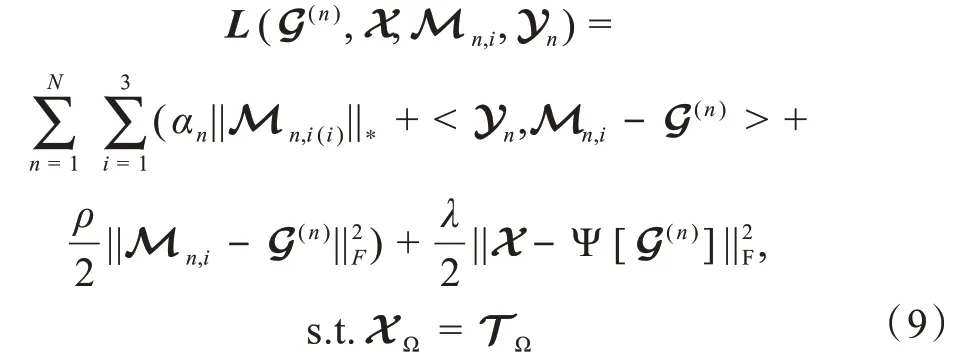
其中Yn是拉格朗日乘子张量，运用交替方向乘子法［14］，按以下方法迭代更新G(n)，Mn,i，X，Yn：

对于每个G(n),k+1,n=1,…,N，只保留有关的项之后，有如下优化子问题，如式（10）所示：

对式（10）求导，取倒数为零的极值点可得式（11）：

上述形式是一个经典矩阵核范数最小化问题，可以直接通过奇异值阈值（singular value thresholding，SVT）得到闭式解［16］，如式（13）所示：

更新恢复的张量X：

得到如下解：

张量X包括已经观测到的部分以及由迭代更新的核心张量生成的缺失部分张量表示。

同时随着迭代过程自动更新ρ，设置步长t，ρ=max{tρ,ρmax}。

3 实验部分

通过进行仿真实验来验证提出算法的性能与并于另外3种算法进行对比，对比算法包括高精度低秩张量补全算法（high accuracy low rank tensor completion，HaLRTC）［17］，以及另外两种同样基于张量链分解进行的张量补全算法：张量链分解加权 优 化 法（tensor train weighted optimization，TTWOPT）［18］，张 量 链 分 解 随 机 梯 度 下 降 法（tensor train stochastic gradientdescent，TTSGD）［19］。本文算法以及对比算法的参数设置如下：权重参数αn均 为10−1，ρ=max{tρ,ρmax}，ρmax=100，t∈[1.1,1.2]寻最优，对比算法的参数设置为程序默认值。另外设置了两个终止条件，停止误差设置为||Xk+1−Xk||/||Xk+1||＜10−6，最大迭代次数maxiter=500。但是根据TTSGD算法的特点以及其算法默认参数设置，可以了解到TTSGD至少迭代105次才能达到与其他算法相近的精确度，为了使实验看上去具有可对比性，所以将TTSGD迭代次数设置为105。实验主要分为两个部分：实际图像恢复效果和合成数据仿真实验。

3.1 实际图像数据

主要进行自然彩色图像的丢失数据估计的应用，并将实际图像用于提出算法与对比算法进行收敛性与运行时间的对比。对图像估计恢复效果的评估主要依据两个评估标准：相对平方误差（relative squared error，RSE）和峰值信噪比（peak signal to noise ratio，PSNR），分别用E和P表示。E=||T−X||F/||T||，X是恢复后的张量，T是原始张量，RSE越小证明恢复效果越好。P=10log10(2552/S)，其 中S=||Treal−X||2F/u(Treal)，u(Treal)表示张量中所有元素的数量，PSNR越大证明实验恢复效果越好。图1为实验测试的RGB图像，均为三阶张量数据。第1个实验在这4个图像数据上进行，设定缺失率为80%，比较4个算法的实际图像恢复效果，图2每行是不同的图像，由左到右每列分别是图像80%缺失效果和本文算法、HaLRTC、TTSGD、TTWOPT算法补全结果，可以直观的看到各个算法在实际图像中补全效果上的差异，可以看出在缺失率较高的时候，肉眼已经很难看出原图的样子，几种算法基本都能恢复出大致的轮廓，但是本文算法与TTWOPT算法明显视觉效果强于另外两种算法。从Lena图中脸部细节和House图中烟囱细节来看，本文算法比TTWOPT局部更加清晰。

图1 实验RGB图像Fig.1 Experimental RGB images

图2 每行的不同图像在80%缺失率时各算法的补全结果Fig.2 Completion results of each algorithm in case of 80%missing rate of different images

第二个实验选取实验大小为256×256×3图像Lena作为对象，进行了多个对比实验，包括不同算法的相对平方误差以及峰值信噪比随采样率从低到高变化的情况（图3），不同算法达到相同误差精度10−6需要的迭代次数以及整个算法运行需要的时间随采样率变化的情况［图4（a，b）］。

图3 算法的RSE和PSNR随采样率变化的对比：（a）RSE，（b）PSNRFig.3 Comparison of RSE and PSNR of algorithms with different sampling rates：（a）RSE，（b）PSNR

由图3可以看出，提出的算法除了在采样率极低（低于20%）的情况下评估标准RSE和PSNR结果都是优于其余3种算法。接下来为了保证迭代次数实验和运行时间实验的准确性，根据TTSGD算法的已知参数设置，可以明显确认该算法的在相同的误差停止条件下，在运行时间和迭代次数两方面都是远远超过其他3种算法的，无需再进行这两方面的对比，因此排除对比算法TTSGD，仅对比本文算法与HaLRTC和TTWOPT3种算法。

图4（a）显示了本文算法与对比算法在收敛性方面的性能对比，在实验结果中，横坐标为各种算法的迭代次数，纵坐标显示每步迭代结果的相对变化值。由此可以看出本文算法迭代速度很快，一般在50次以内就收敛了，但是相同条件下也是基于张量链分解的TTWOPT算法收敛迭代次数将近300次。图4（b）对比了3种算法在不同采样率下的运行时间，从运行效率的角度看，整体上是采样率越高耗时越短，计算相对简单的HaLRTC需要的时间并不长，采样率较高时本文算法略快于HaLRTC，整体说来差距并不明显。但是对比运算同样较复杂的TTWOPT算法，本文算法在运行时间实验上表现的性能明显优于TTWOPT算法。

图4 （a）图像缺失率50%时各算法收敛性分析对比，（b）算法运行时间随采样率变化的对比Fig.4（a）Convergence analysiscomparison of algorithms at 50%missing rate，（b）comparison of algorithms running time with different sampling rates

3.2 合成数据

考虑用人工合成数据验证该算法的有效性，首先通过张量链分解的方式分别生成四阶和三阶的2个实验张量 X∈ℝ50×50×50×50和 Y∈ℝ80×80×80，其中核心张量都独立服从标准正态高斯分布，通过对核心张量的运算Ψ[G(n)]得到实验张量，对合成数据采用RSE作为性能评估标准。考虑到实验的随机性，每个实验数据的结果都是取10次实验的平均结果。由图5（a）和（b）分别给出了算法在四阶和三阶张量情况下的对比实验结果，结果表明，本文算法除了在采样率极低的情况（20%以下）性能一般，除此以外表现稳定，恢复精度明显高于其他3种算法。而较其他3种算法需要千倍以上迭代次数的TTSGD，由于在本次对比实验中需要的迭代次数太多而被提前终止，表现得极其不稳定并且精度较差。

图5 合成张量数据上各算法的RSE随采样率变化的对比：（a）四阶张量，（b）三阶张量Fig.5 Comparison of RSE of each algorithm on synthetic tensors with different sampling rates：（a）fourth-order tensor，（b）third-order tensor

4 结 论

以上对基于张量链分解对缺失张量进行了低秩张量补全的研究，该算法在张量链分解的核心张量上采用了低秩约束方法，并通过凸松弛转换为核心张量核范数最小化求解，这样能够有效降低高阶张量的计算规模。实验表明，本文方法运行时间更短，迭代收敛更快，补全结果也比较好，综合各方面性能均优于对比算法。