一类Klein-Gordan方程的精确解*
张 娟,杨吉英
(①昆明理工大学津桥学院理工学院,650106,昆明市;②保山学院数学学院, 678000,云南省保山市)
0 引 言
Klein-Gordan方程是由瑞典理论物理学家奥斯卡·克莱因和德国人沃尔特·戈登于1927年分别独立推导得出的.Klein-Gordan方程是相对论量子力学和量子场论中最重要的数学模型之一.有许多积分变换方法可以求解常微分方程、偏微分方程和积分方程[1-8].同时,许多学者提出了不同的方法来处理各种类型的Klein-Gordan方程,如约化微分变换法(RDTM)[9]、变分迭代法(VIM)[10-11]、Adomian分解法(ADM)[12]、改进的Adomian分解法(MADM)[13]和自然分解法(NDM)[14,15].
Adomian分解法是由美国数学物理学家George.Adomian提出的,自提出以来已被应用于求解各种数学物理问题.用该方法得到的解一般为级数形式,具有很好的收敛性且便于计算.自然变换(Natural transform)[6]是一种类似于Laplace变换和Sumudu变换的新的积分变换,这种积分变换的特点是其收敛于Laplace变换和Sumudu变换.自然分解法是自然变换法和传统的Adomian分解法的结合.本文通过两个例子来说明这种方法的有效性和准确性,并与已有的结果进行了比较.
1 自然变换
定义1.1[6-8]设f(t) 当t≥0时有定义. 称
为函数f(t)的自然变换,其中f(t)∈A,而
A={f(t)|∃M,τ1,τ2,使得|f(t)| 若R(s,u)是f(t)的自然变换,则称f(t)为R(s,u)的逆变换. 下面,给出自然变换的一些基本性质. 定理1.2[6-8]若R(s,u),F(S)分别是f(t)∈A的自然变换和Laplace变换,则 定理1.3[6-8]若R(s,u),G(u)分别是f(t)∈A的自然变换和Sumudu变换,则 定理1.6[6-8]若a,b是非零常数,f(t) 与g(t) 是A上的函数,则 N+[af(t)±bg(t)]=aN+[f(t)]±bN+[g(t)]. 下面介绍自然分解法[14,15].考虑下面的非线性非齐次Klein-Gordan方程 vtt(x,t)-vxx(x,t)+cv(x,t)+Fv(x,t)=h(x,t), (1) v(x,0)=f(x),vt(x,0)=g(x), (2) 这里,t是时间变量,s是空间变量,c是常数,F代表一般的非线性微分算子,h(x,t),f(x),g(x)是源项. 方程(1)式两边同时取自然变换,有 (3) 将方程(2)代入方程(3),得 (4) 方程(4)两边同时取逆变换,有 (5) 其中H(x,t)来自源项. 设 (6) 引入Adomian多项式来表示非线性项 (7) 其中 (8) 将(6),(7)式代入方程(5),得 (9) 比较方程(9)两边,得 以此类推, 下面将自然分解法应用于求解线性及非线性Klein-Gordan方程. 例1 考虑下面的非齐次线性Klein-Gordan方程[12] vtt(x,t)-vxx(x,t)+v(x,t)=2cosx, (10) 其初始条件为 v(x,0)=cosx,vt(x,0)=1. (11) 首先,方程(10)两边取自然变换,得 (12) 将式(11)代入方程(12),有 (13) 方程(13)两边同时取逆变换,得 (14) 设 (15) 结合(14),(15)式得 (16) 比较(16)式两边,有 v0(x,t)=cosx+sint+cosx(1-cost), 以此类推, (17) 由(17)式,计算得 以此类推,可以得到以下级数形式的解 v(x,t)=v0(x,t)+v1(x,t)+v2(x,t)+…. 另外,通过消去v0(x,t)和v1(x,t)之间的噪声项,发现v0(x,t)的剩余部分仍然是原方程的解.于是得到原方程的精确解v(x,t)=cosx+sint.这与文献[13]中通过改进的Adomian分解法(MADM)得到的结果是一致的. 例2 考虑下面的非齐次非线性Klein-Gordan方程[12] vtt(x,t)-vxx(x,t)+v2=1+2xt+x2t2, (18) 其初始条件为 v(x,0)=1,vt(x,0)=x. (19) 首先,方程(18)两边取自然变换,得 (20) 将式(19)代入方程(20),有 (21) 方程(21)两边同时取逆变换,得 (22) 设 (23) 结合(22),(23)式得 (24) 其中An是表示非线性项v2的Adomian多项式. 比较(24)式两边,有 于是 (25) 由式(25),计算得 以此类推,可以得到以下级数形式的解v(x,t)=v0(x,t)+v1(x,t)+v2(x,t)+…. 另外,通过消去v0(x,t)和v1(x,t)之间的噪声项,发现v0(x,t)的剩余部分仍然是原方程的解.于是得到原方程的精确解v(x,t)=1+xt.这与文献[13]中通过改进的Adomian分解法(MADM)得到的结果是一致的. 本文利用自然分解法,研究了一类Klein-Gordan方程的精确解.通过两个例子验证了该方法的有效性和准确性.我们将致力于更一般化的模型,以供将来的研究,并将此方法应用于其他非线性偏微分方程的求解.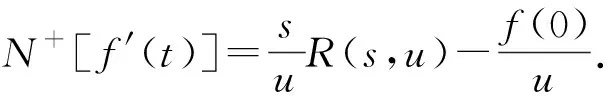
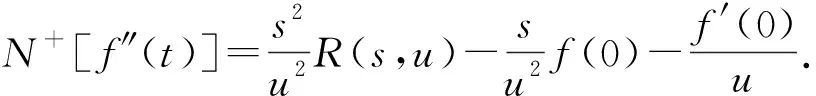
2 自然分解法
3 应用举例
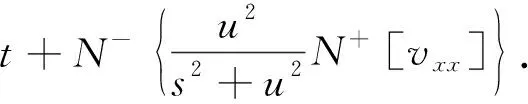

4 结 论

