多导体传输线串扰概率分布计算方法
高 乐, 于全毅, 魏庆丽, 刁 庶
(吉林大学仪器科学与电气工程学院,长春130061)
0 引 言
实验设备中存在大量可视为多导体传输线(multiconductor transmission lines,MTLs)的平行多导线、微带线等,随着实验设备的大量使用,近年来实验设备中传输线的电磁兼容问题越来越受到研究人员的重视,其中串扰是多导体传输线之间由于电磁相互作用而产生的电磁干扰,严重时会影响设备的正常工作。针对多导体传输线的电磁兼容问题,Antonini等[1]、Paul[2]在多导体传输线理论的创建和完善方面做出了杰出的贡献。Tesche等[3]基于电磁结构分析提出了Beam-Liu-Tesche(BLT)方程,实现了对传输线的终端响应分析。针对多导体传输线串扰的不确定性问题,传统的蒙特卡洛法[4-6]已经实现了对传输线串扰的概率分布预测,但是蒙特卡洛法(Monte Carlo,MC)的计算成本十分昂贵。为了解决这一问题,Larbi等[7]采用可靠度法对多导体传输线的失效概率与灵敏度进行了分析。Fei等[8]结合随机降阶法对多导体传输线串扰的不确定性进行了量化分析。另外还有最大熵法[9]、随机配置法[10]和干涉式混沌多项式法[11]等其他统计学方法成功应用于传输线电磁耦合的不确定性问题分析。
本文提出采用非干涉式的广义混沌多项式展开法计算实验设备中传输线串扰响应的概率密度函数,广义混沌多项式展开法能够有效地建立代理模型,基于代理模型对多导体传输线串扰的相关统计参数进行计算,并高效准确地得到多导体传输线串扰概率分布函数。
1 广义混沌多项式展开法(Generalized Polynomial Chaos Expansions Method,gPCE)
Wiener[12]最早提出了混沌多项式理论,并基于Hermite正交多项式构建了混沌多项式,最初的混沌多项式中的变量均服从于正态分布,当输入变量不服从正态分布时,Wiener混沌多项式的计算速度较慢,且计算得到的结果也不够准确。Xiu等[13-14]通过Askey方案将输入变量的分布类型推广至更多传统的分布类型,相较于最初的混沌多项式,该方法能够有效地应用于其他分布类型,得到了应用范围更加广泛的广义混沌多项式。非干涉式的广义混沌多项式能够将模型视为黑箱,仅需关注输入变量与输出变量间的映射关系,不需要对黑箱内部的函数关系进行改动,因此得到了广泛的应用。
令原始模型Y=y()ξ,采用gPCE对该模型进行展开:
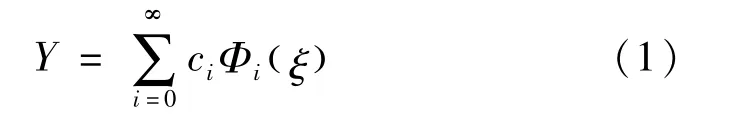
式中:Φi()ξ为各个随机变量所对应的一维标准正交多项式基函数的乘积;ci为各个展开项Φi()ξ的系数。
当采用广义混沌多项式法对模型进行展开计算时,混沌多项式的项数是无穷的,为保证计算准确度与计算效率,应当人为的设定一个适当的截断阶数,将展开式中多项式的最高阶数设置为P,减少混沌多项式展开项的项数。因此令截断阶数为P,截断后的gPCE模型为:
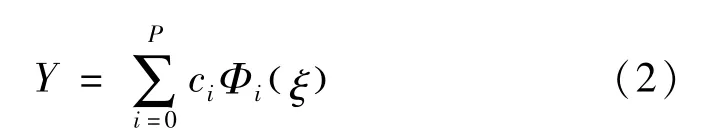
令P阶截断后的混沌多项式的项数为Q,Q随着截断阶数P与输入变量维度d的增加而增长:
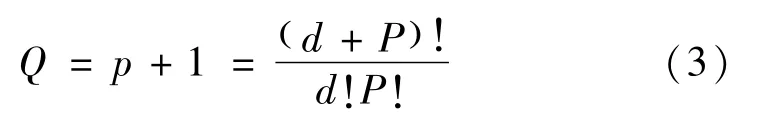
当构建好混沌多项式展开模型后,可以采用不同的计算方法对展开后的多项式的系数进行计算,在计算非干涉式混沌多项式时比较常用的方法为回归法。本文采用回归法中的随机响应面法对展开项的系数进行计算。
随机响应面法首先需要在标准随机空间中选取有效的N个样本点,式中S为被标记的量为样本点。常用的采样方案为Sobol采样与拉丁超立方采样以及蒙特卡洛采样,Hosder等[15]认为采用两倍于多项式项数的过采样方案即可达到满意的计算准确度。本文采用拉丁超立方采样方案。
进行采样后将标准随机变量空间ξ中转换至原随机空间X,得到原随机变量空间中的样本点:XS=,在X空间中调用原函数的响应模型g()
X,计算得到样本空间X中的函数响应值为
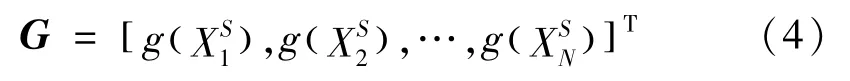
采用最小二次回归法对多项式的系数进行估算。令多项式系数向量为将样本空间ξ与相应的函数响应值G分别代入式(2),可以得到

式中:
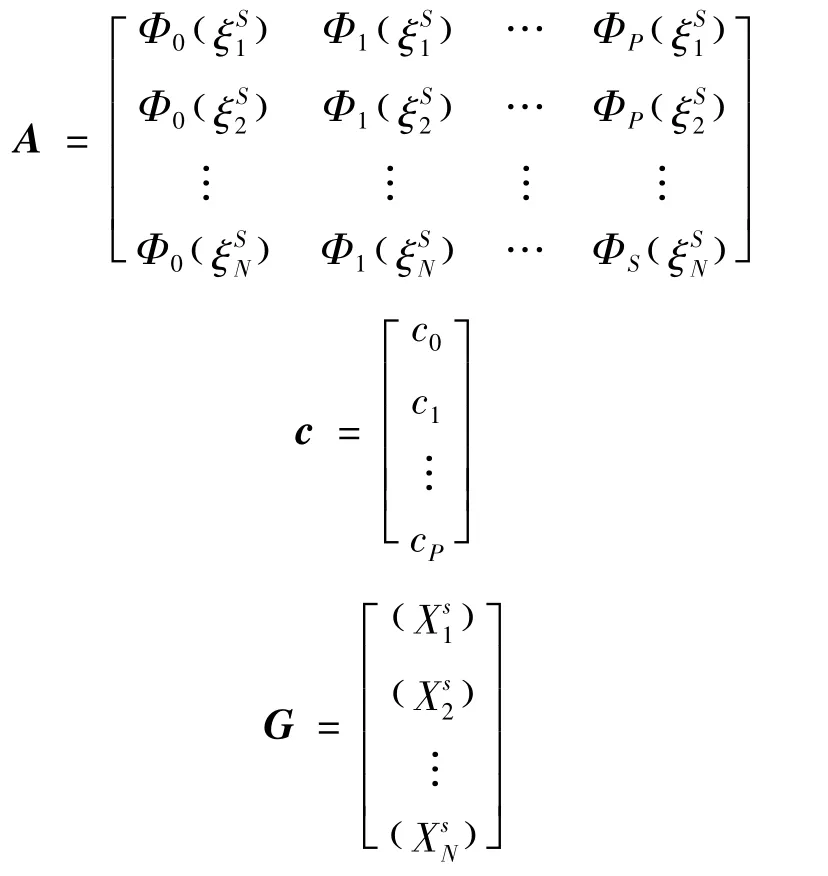
根据线性最小二次回归法对多项式的系数进行求解,可以得到:
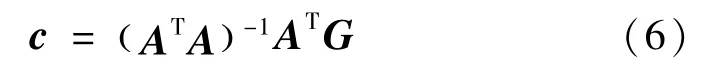
计算得到多项式系数后,即可通过蒙特卡洛法对广义混沌多项式代理模型的相关统计参数进行计算,其中模型响应的平均值μ与标准差σ为:
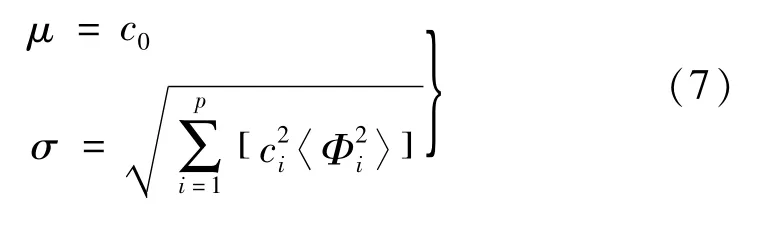
2 数值算例
结合上一节中介绍的非干涉gPCE对多导体传输线串扰的数值算例进行计算,多导体传输线串扰模型如图1(a)、(b)所示。
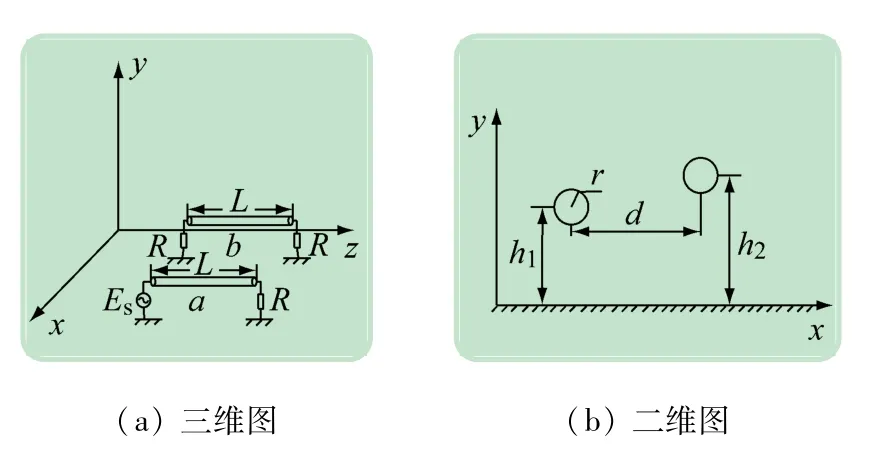
图1 以地面为参考导体的传输线结构
该模型是典型的多导体传输线模型,由参考导体与传输线组成,其中参考导体为无限大的地面,传输线均为无耗均匀传输线,其中传输线a上带有激励源Es,且Es=1 V。图中:d为两根传输线之间的横向距离;h1、h2分别为两根传输线距离地面的高度;R为传输线两端的负载阻抗;r为传输线的半径。为了方便进行仿真计算,令2根传输线的半径相等,并且传输线的远端与近端的端接阻抗也相同,均为50 Ω。
在实验设备的生产与加工中,设备中的传输线的捆扎与布置具有一定的随机性,导致上述的传输线对地高度h1、h2、传输线之间的横向距离d以及传输线的半径r具有不确定性,可能导致系统的电磁兼容性出现严重的问题,结合第1节中介绍的非干涉gPCE建立多导体传输线串扰的代理模型并对相关的统计参数进行计算。针对实验设备中传输线可能存在的不确定性,本文将上述的传输线对地高度h1、h2、传输线之间的横向距离d以及传输线的半径r 4个变量设为随机输入变量,即变量维度n=4,并令不同的变量服从对应的随机分布:h1、h2服从服从服从N(0.4 mm,0.1 mm)。
以传输线b的远端感应电流i2为例,采用非干涉gPCE建立图中多导体传输线串扰的代理模型,对i2的相关统计参数进行计算。本文采用采样点数为400的拉丁超立方采样法。在采用gPCE进行计算时,模型的计算准确度与计算成本也会随着截断阶数P的增加而增加。为了平衡计算准确度与计算效率之间的关系,需要选取合适的混沌多项式的截断阶数P,因此本文将选取部分截断阶数与MC的计算结果进行对比。接下来分别令截断阶数P为2、4以及6,对多导体传输线串扰的均值与标准差进行计算。将传输线所处的入射场的频率范围设置为10 MHz~1 GHz,将不同截断阶数P情况下gPCE的计算结果与传统的MC法进行对比,MC的仿真次数为20 000次。对比结果如图2(a)、(b)所示。
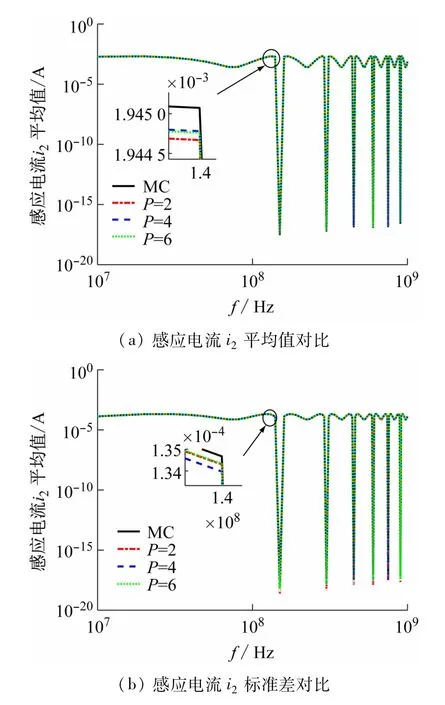
图2 感应电流i2平均值与标准差对比
由图2可见,对于传输线b的远端感应电流i2的平均值与标准差计算结果来说,当多项式的截断阶数P=2时,gPCE的计算结果与20 000次蒙特卡洛法的计算结果基本一致,并且随着截断阶数P的增加,两种方法之间的计算结果并没有明显的差异,说明当截断阶数P=2时,gPCE的计算结果便达到了传统的MC法的计算准确度,在接下来的计算分析中,将截断阶数P设置为2。
在计算得到10 MHz~1 GHz频段中i2的平均值与标准差之后,针对该频段中50、200以及800 MHz 3个频点处i2的概率密度函数进行计算,同上文中一样,将计算结果与传统的MC法进行对比,对比结果如图3所示。由图3可见,利用gPCE计算得到的不同频点处的概率密度函数与MC的计算结果基本一致,并且同时对比不同频点处的计算时间,见表1。
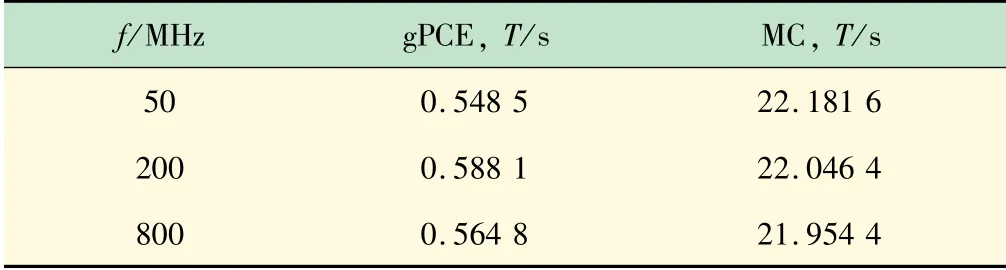
表1 不同频点处2种方法计算时间对比
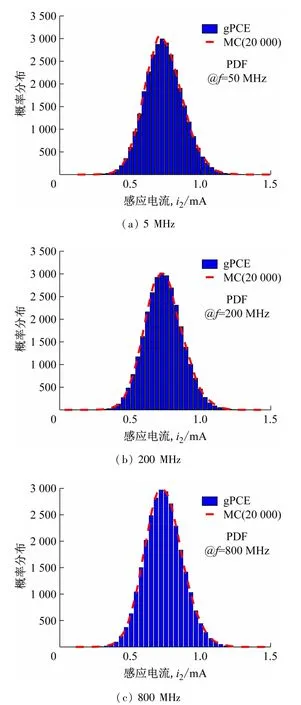
图3 不同频点处感应电流i2概率分布函数对比
由此可见,gPCE不仅能够有效地计算得到多导体传输线串扰的概率密度函数,并且相较于20 000次MC,gPCE所需要的计算时间更少,大幅提高了计算效率。同理,多导体传输线串扰各个频点上的概率分布都可以通过上述的方法得到,并且在10 MHz~1 GHz区间,[μ+3σ,μ-3σ]也可以作为串扰响应值的上下限,如图4中的红色曲线所示。
由图4可见,MC法仿真得到的曲线大部分都包含在[μ+3σ,μ-3σ]中,证明[μ+3σ,μ-3σ]能够有效地作为串扰响应值的上下限。通过上述计算分析,证明本文所采用的非干涉gPCE能够准确、高效地计算多导体传输线串扰不确定性问题中涉及到的相关统计参数,如串扰感应电流(感应电压)的平均值、标准差与概率分布函数,在工程应用中,可以结合本文所用方法,对实验设备中的传输线位置进行合理的设计或调整,尽量减少实验设备中传输线发生的电磁兼容现象。
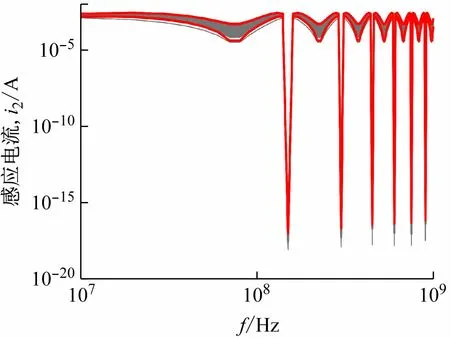
图4 感应电流i2变化范围
3 结 语
本文采用非干涉gPCE法对多导体传输线串扰的不确定性进行了研究,并得到了准确的串扰的相关统计特征参数,验证了非干涉gPCE的有效性。针对传输线对地高度h1、h2,传输线间的横向距离d以及传输线半径r等随机输入变量,建立传输线串扰的代理模型,并利用代理模型计算得到频段10 MHz~1 GHz中感应电流的均值与标准差等统计参数,同时也计算得到不同频点处的串扰概率分布情况。通过与传统的MC对比可知,本文采用的方法能够达到MC的计算准确度,并且明显缩短了计算时间,证明本文提出方法在多导体传输线串扰概率分布计算方面是正确、高效的。

