用变换思想引领几何问题解决的思考过程

段春炳 王红权

摘  要：“图形的变化”是“图形与几何”领域的三大模块之一，内容贯穿初中三年的几何教学. 图形的性质反映为在某种变换下保持不变的性质，从变换的视角考察图形的形成、结构和性质更能抓住问题的本质. 在教学中，教师可以从单元整体视角设计系列探究活动，促进学生从整体上理解图形的变化的概念和性质，建立动态几何观念，灵活解决几何问题.

关键词：图形的变化;变换思想;问题解决

在《义务教育数学课程标准（2011年版）》（以下简称《标准》）中，“图形的变化”是“图形与几何”领域的三大模块之一，内容包含图形的轴对称、旋转、平移、相似和投影. 浙教版《义务教育教科书·数学》（以下统称“教材”）中，将平移安排在七年级下册、轴对称安排在八年级上册、中心对称安排在八年级下册、旋转和相似安排在九年级上册、投影安排在九年级下册，整体安排呈螺旋式上升. 由于时间跨度大，不同图形变化有不同的载体，因此，新课教学中不能很好地引导学生从整体性上对图形进行认识. 作为中考复习，一方面，图形的变化复习重点要基于单元的整体性，提升学生对于图形的变化内容的理解和应用能力;另一方面，图形的变化贯穿了几何教学的全部内容，图形的性质一般是变换性质的反映，因此，可以用变换的思想去引领几何复习教学和几何问题的解决.

一、图形的变化及对变换思想的理解

1. 对图形的变化内容的本质理解

就平面几何而言，按照德国数学家F.克莱因于1872年提出的观点，平面几何是研究平面图形在运动、变化过程中的不变性质和不变量的科学. 在轴对称、旋转和平移变换下保持任意两点之间的距离不变，这样的变换称为等距变换，等距变换也保持角的大小不变. 在等距变换下，不改变图形的大小、形状和相对位置等，这些不变性正是我们所要研究的.

在初中阶段，轴对称、平移和旋转是作为研究图形性质、关系的有力工具. 正如《标准》中指出的要“探索等腰三角形、矩形、菱形、正多边形和圆的轴对称性质”“探索线段、平行四边形、正多边形和圆的中心对称性质”. 通过这些图形对称性的探索能使学生更好地理解这些图形的性质.

《标准》中还指出，要“认识并欣赏自然界和现实生活中的轴对称图形和中心对称图形”“认识并欣赏平移在自然界和现实生活中的应用”“运用图形的轴对称、旋转、平移进行图案设计”. 事实上，图形的变化在计算机图形学、计算机辅助设计、机械工程、航空制造等领域都有广泛的应用.

2. 图形的变化中蕴涵的思想方法和育人价值

轴对称、旋转、平移、相似和投影都是对图形运动变化下不变的量和不变的关系的研究.“变中不变”是图形变换的基本思想之一，这里的“变”通常是指图形的位置有规则的发生变化，“不变”是指图形经过变换后不变的关系和量，也称为不变量思想.

通过图形的变化实现图形位置的转化，可以把一般情形转化为特殊情形，使分散的条件集中到一个三角形（或四边形等）中，使问题化难为易，体现了转化思想.

轴对称图形、中心对称图形、旋转对称图形等由图形的一半（或部分）就能确定图形的另一半（或部分），利用一半（或部分）图形的信息解决问题就是对称思想，对称思想在图形的变化中体现的非常明显和直接.

不同的图形变换，从定义到性质，再到应用，都有共通性，能很好地体现类比思想.

图形的变化的内容有利于培养学生的“运动变化”“变中不变”等思想. 在图形的变化的学习过程中积累的相关直观感知经验是培养学生空间想象、几何直观和动态几何观念的重要途径. 在图形的变化内容的学习中，让学生感受图形的对称和数学的对称美，进而提升学生的数学审美能力. 应用图形的变化的知识解决具体问题往往需要学生综合而灵活地应用所学知识，这对于培养学生的创新意识具有很好的作用.

二、复习教学目标及整体设计

“图形的变化”内容包括軸对称、旋转、平移、相似和投影，前三种都是全等变换. 本文仅考虑轴对称、旋转和平移的综合复习.

根据《标准》的要求，结合上述图形的变化的作用和地位，以及图形的变化中蕴涵的数学思想方法和育人价值，基于单元的教学设计，从宏观到中观，再走向微观，使抽象观念变为具体可操作的行为，确定图形的变化综合复习的教学目标如下.

（1）从整体视角理解平移、旋转（中心对称）、轴对称的概念和性质，理解在这几种图形的变化下图形保持形状和大小不变的本质.

（2）从图形的变化的视角理解图形的结构和性质. 例如，等腰三角形有轴对称结构，也有旋转的结构（共端点，等线段）;等边三角形有轴对称结构，也有旋转对称结构;平行四边形有平移的结构，也有中心对称的结构，等等.

（3）探索平移、旋转和轴对称三种变换之间的关系，进一步从整体上理解图形的变化的性质.

（4）能灵活、综合应用图形的变化的性质解决具体问题，并从中感受应用图形的变化解决问题带来的简便和优美.

（5）通过经历相关的探究活动，提高学生发现问题、提出问题、分析问题和解决问题的能力.

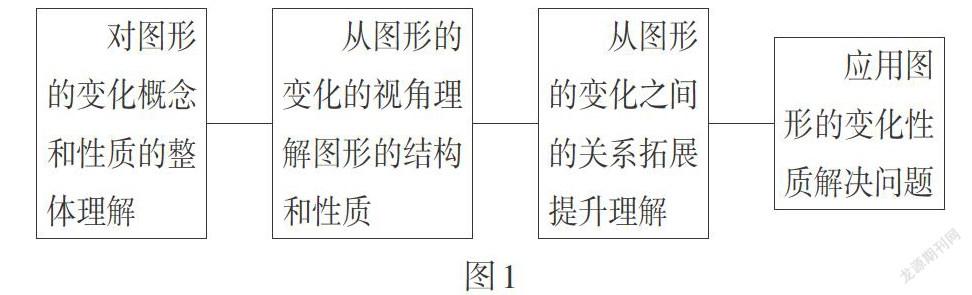
“图形的变化”内容的复习教学在整体上设计为如图1所示的四个板块.

三、探究性活动的设计和实施

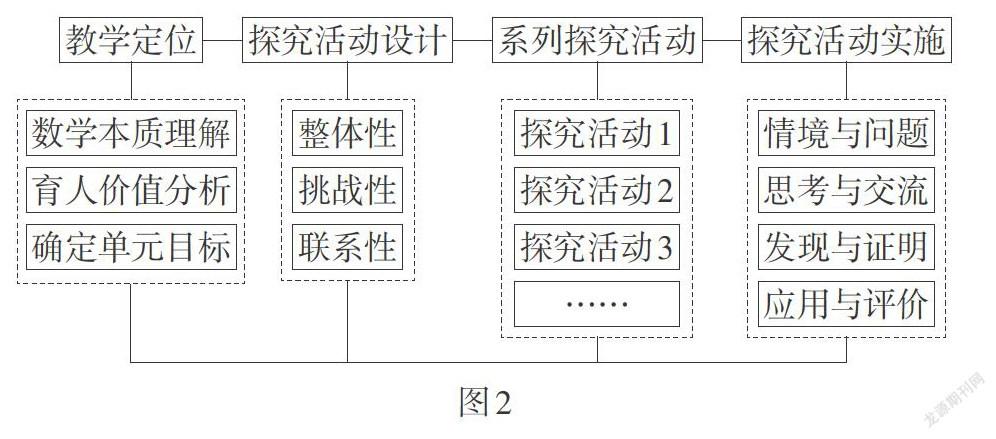
1. 基于单元整体的探究活动设计

单元教学设计的特点要求从整体上构建反映数学本质的、有联系的和具有挑战性的系列探究活动，其设计框架如图2所示.

2. 探究性活动的实施

活动1： 图形的变化性质的再探究.

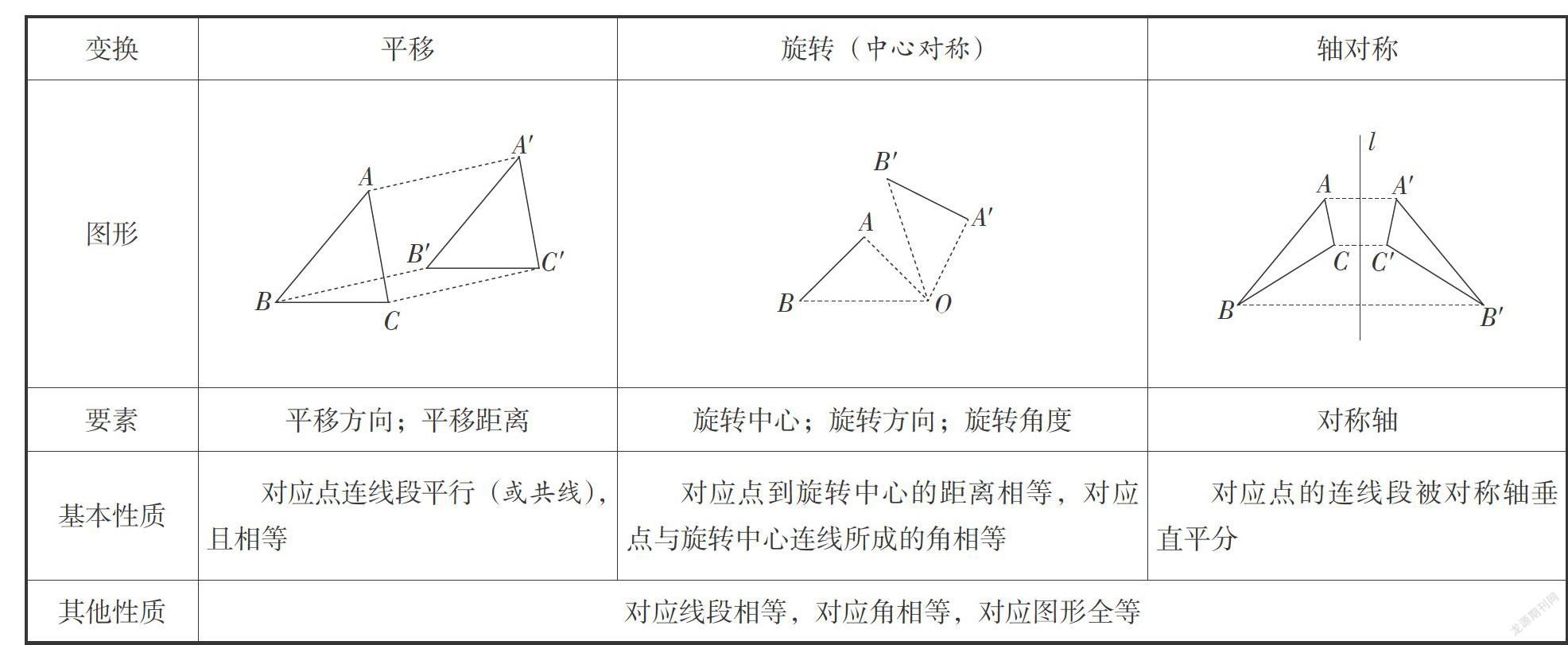
情境与问题：比较平移、旋转和轴对称这三种变换的性质，找出它们的相同点和不同点. 在比较的过程中，你还有什么发现？

思考与交流：学生通过独立思考和相互交流，得到这三种变换性质的相同点和不同点. 具体如下表所示.

从上表中可以看出，三种变换的相同点如下.

（1）对应线段相等，对应角相等，对应图形全等.

（2）所研究的对象是相同的，都是关于对应点、对应线（或线段）、对应角和对应图形.

（3）基本性质都是关于对应点的，且是关于对应点与变换要素之间的关系.

在平移变换中容易得到对应线段不仅相等，而且平行（或共线），那么在旋转和轴对称中，对应线段除了相等，是否还有其他的性质？

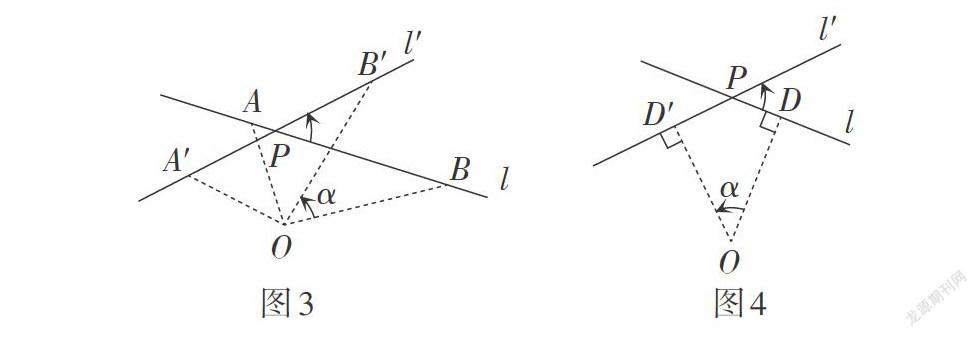
发现与证明：在轴对称变换中，对应线段与对称轴平行（或共线），或对应线段的交点（对应线段延长线的交点）在对称轴上（即对称轴平分对应线段所夹的角）. 在旋转中，对应线段（直线）的夹角等于旋转角.

旋转的这个性质应用较为广泛，要求学生给出证明. 学生从旋转作图方法的不同，给出了如图3和图4所示的两种情况的证明，证明过程略.

应用与评价：你能应用旋转的这个性质解决一些问题吗？试举例说明.

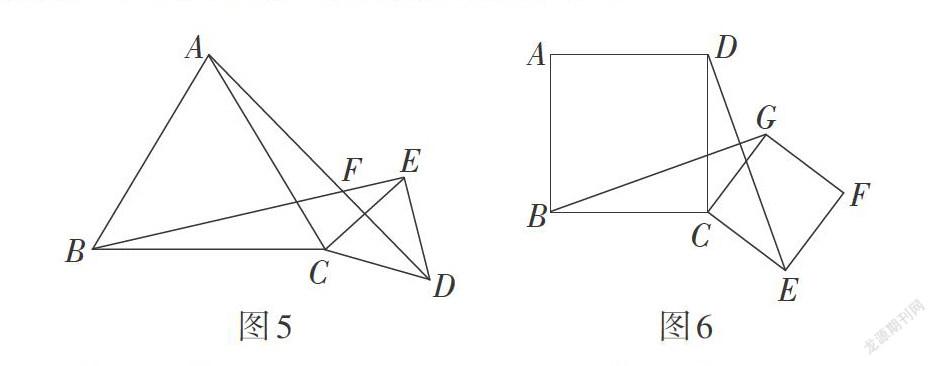
如下面两道经典例题.

例1  如图5，△ABC和△CDE都是等边三角形，则AD = BE，且AD与BE的夹角为60°.

例2  如图6，在正方形ABCD和正方形CEFG中，则DE = BG，且DE ⊥ BG.

虽然这两道例题都可以用全等的知识来证明，但是用旋转解释则非常直观.

通过这个活动，学生进一步探究了图形的变化的性质及其应用，并且对图形的变化的认识更加整体和深入. 平移、旋转和轴对称的共同性质反映了这三种变换的本质，这样全等和变换这两个知识模块就成为一个整体. 在比较中，学生清楚地感受到研究图形的变化在方法上的一致性. 例如，研究对象相同——都是研究对应点、对应线、对应角和对应图形;基本性质研究的角度相同——都是研究对应点与變换要素的关系，都是研究要素及相关要素（对应线、对应角）的数量关系和位置关系. 这样获得的知识具有整体性和系统性，能更好地迁移到新的问题情境中去解决问题.

【设计意图】通过类比引导学生发现问题、提出问题、分析问题和解决问题，并能应用在具体问题的解决中. 这个探究过程进一步从整体上加深了学生对图形的变化性质的理解.

活动2：从图形的变化的视角理解图形的结构和性质.

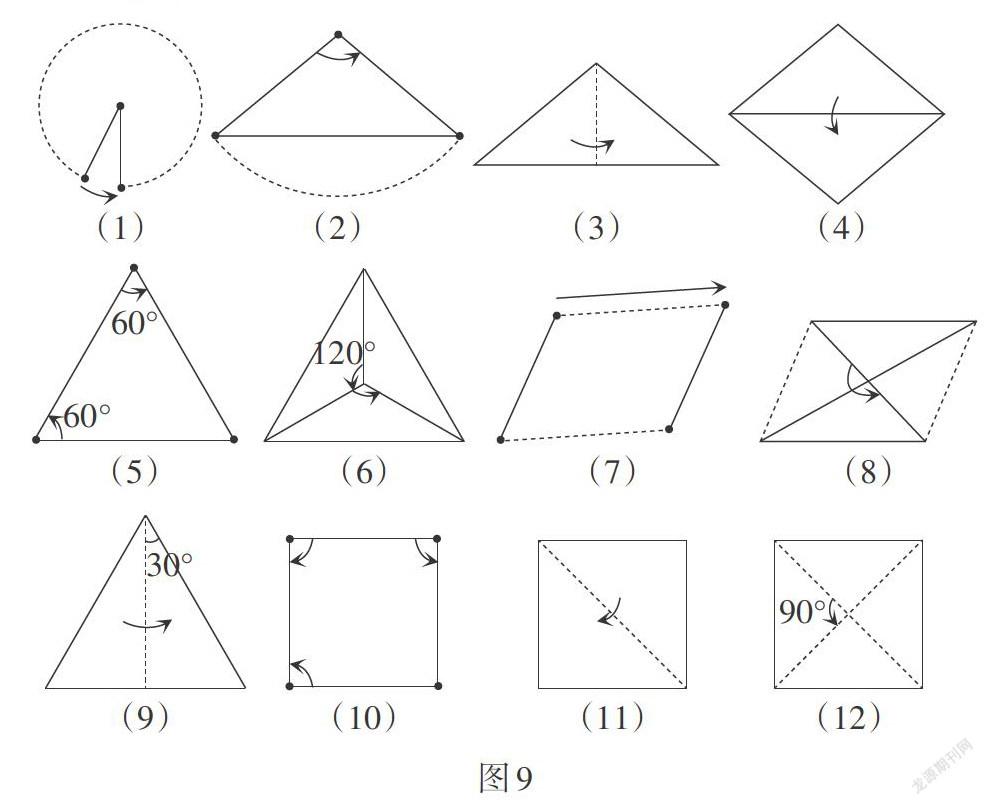
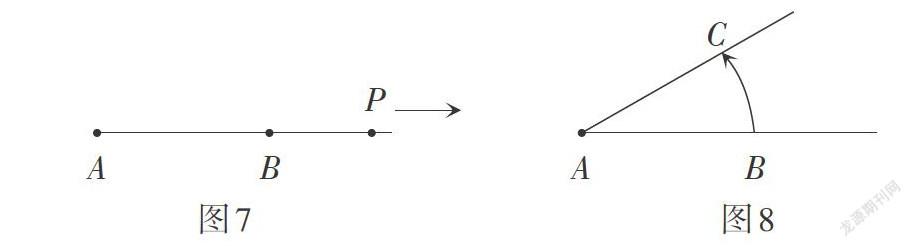
情境与问题：观察几何画板软件的动画演示（如图7，图8），点沿着一个方向平移一定的距离得到一条线段，继续平移且不停止则得到一条射线;射线绕着端点逆时针旋转一定的角度得到一个角. 试从一条线段出发，通过平移、旋转和轴对称中的一种或几种变换形成我们所熟悉的图形.

思考与交流：学生边思考边在纸上尝试画图. 然后交流展示. 对于常见图形，学生能够从变换的视角理解它的形成与结构. 例如，图9（1）为线段绕一个端点旋转一周形成圆;图9（2）为线段绕一个端点旋转一个角度形成等腰三角形;图9（3）为等腰三角形关于底边上的中线翻折产生直角三角形;图9（4）为等腰三角形关于底边翻折生成菱形;图9（5）为等边三角形其可以由一条线段连续两次旋转60°得到;图9（6）表示等边三角形也可以由顶角为120°的等腰三角形绕顶点连续两次旋转120°得到;图9（7）表示由线段平移得到平行四边形;图9（8）表示的平行四边形也可以是三角形绕一个顶点旋转180°（中心对称）得到，等等.

发现与证明：在这个探究过程中，发现等边三角形绕中心旋转120°后能与原三角形重合，正方形绕中心旋转90°后能与原正方形重合. 这样我们就清楚了等边三角形不仅具有轴对称性，还有旋转对称性. 容易推广到正多边形都具有旋转对称性. 证明是显而易见的.

应用与评价：你能应用正多边形的旋转对称性解决问题吗？试举例说明.

比较上述两种证法，前者是静态的，后者是动态的. 前者用的知识有等边三角形的边角关系、全等、三角形内角和外角的关系等，后者用的是等边三角形的旋转对称性和旋转的性质. 我们可以看出后者把握了图形的基本结构（旋转对称性），能够从整体上处理图形中相关元素之间的关系，所以能更直接的获得相关元素之间的关系.

学生经历了探究活动后，能利用所学使静态的图形动起来，更好地认识和把握住图形的本质结构，从而容易发现图形中元素之间的相互关系.

【设计意图】从图形的变化的角度重新审视图形的形成和结构，从而使学生从动态的、变化的角度理解图形，提升学生的几何直观和空间想象能力.

活动3：探究图形各种变化之间的联系.

情境与问题：在活动2中，我们已经发现平行四边形可以由线段平移得到，也可以由三角形中心对称得到，那平移和中心对称有怎样的关系？不同的变换之间是否会有一些关系？

思考与交流：学生分组进行探究，分别探究平移与旋转（中心对称）、平移与轴对称、轴对称与旋转的关系. 先进行小组内交流，再进行全班交流，最终获得如下成果.

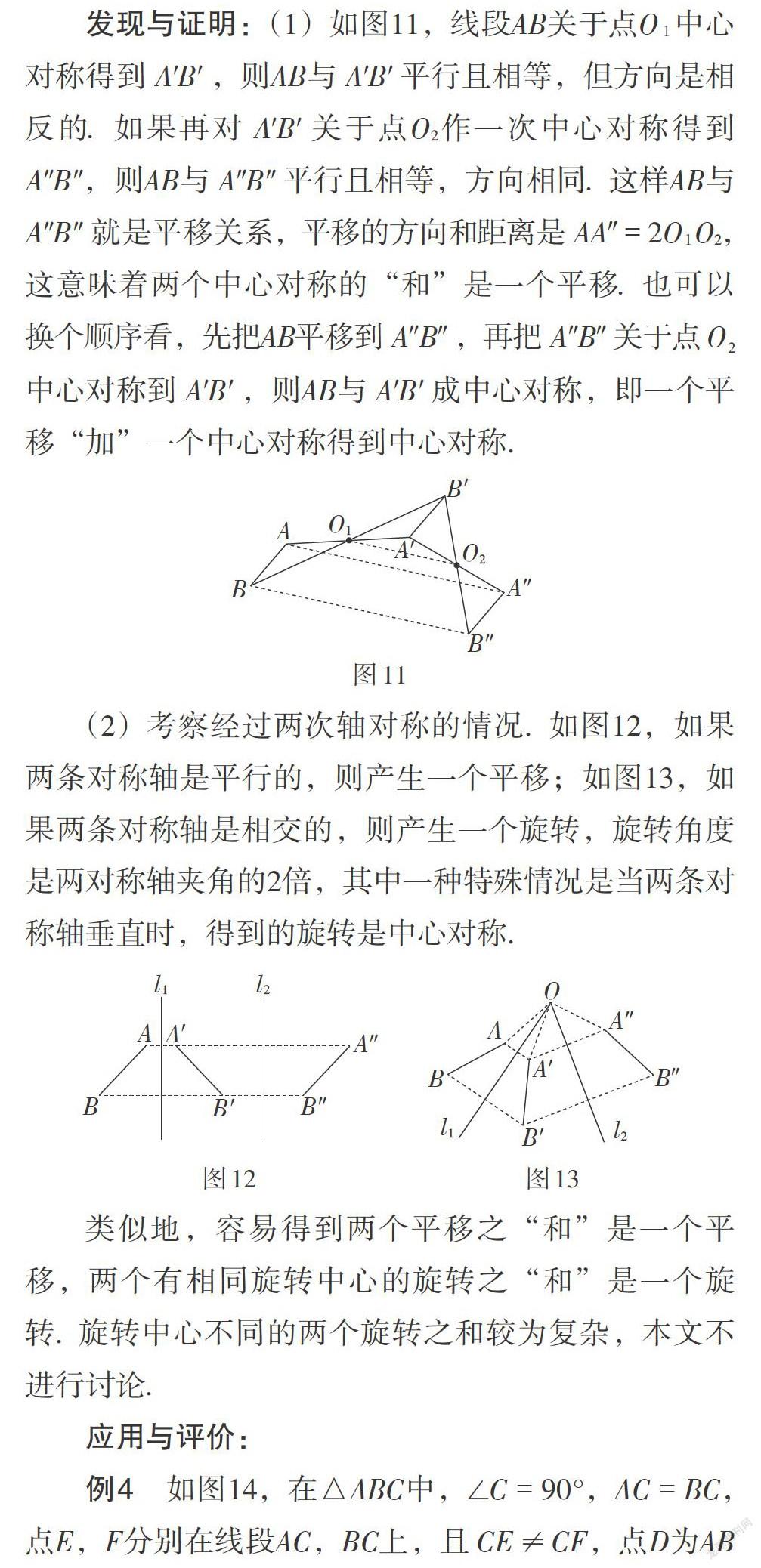
发现与证明：（1）如图11，线段AB关于点O1中心对称得到[AB]，则AB与[AB]平行且相等，但方向是相反的. 如果再对[AB]关于点O2作一次中心对称得到[AB，] 则AB与[AB]平行且相等，方向相同. 这样AB与[AB]就是平移关系，平移的方向和距离是[AA″]= 2O1O2，这意味着两个中心对称的“和”是一个平移. 也可以换个顺序看，先把AB平移到[A″B″]，再把[A″B″]关于点[O2]中心对称到[AB]，则AB与[AB]成中心对称，即一个平移“加”一个中心对称得到中心对称.

（2）考察经过两次轴对称的情况. 如图12，如果两条对称轴是平行的，则产生一个平移;如图13，如果两条对称轴是相交的，则产生一个旋转，旋转角度是两对称轴夹角的2倍，其中一种特殊情况是当两条对称轴垂直时，得到的旋转是中心对称.

类似地，容易得到两个平移之“和”是一个平移，两个有相同旋转中心的旋转之“和”是一个旋转. 旋转中心不同的两个旋转之和较为复杂，本文不进行讨论.

【设计意图】探究平移、旋转、轴对称等不同变换之间的联系，进一步深入理解图形变化的性质和图形的性质.

活动4：灵活应用“图形的变化”解决问题.

例6  如图23，点D，E，F分别是△ABC三边AB，BC，CA的中点，O1，O2，O3分别是△ADF，△BDE，△CEF的外心，I1，I2，I3分别是这三个三角形的内心. 求证：△O1O2O3 ≌ △I1I2I3.

例6的探究过程的要点阐述如下.

学生看到此题的第一感觉是这道题目很难，平时遇到一个外心（或内心）都会感到不熟悉，更何况此题中出现了三个外心和三个内心. 有些学生会被这些“假象”吓住，不敢进一步思考. 有少数学生会从外心或内心的概念出发，通过构造全等三角形得到O1O2平行且等于[12]AB，从而进行证明. 但图形和说理过程会有些杂乱. 当然，O1O2平行且等于[12]AB是解题的关键，如果学生想不到这一点，可以作为铺垫让学生观察和说理. 在这个基础上引导学生发现图形中平移的结构——△ADF以AD（[12AB]）为方向和距离平移得到△DBE，则这两个三角形的外心O1，O2为对应点，所以O1O2 =[12]AB. 同理，I1I2 =[12]AB. 所以O1O2 = I1I2. 同理，O1O3 = I1I3，O2O3 = I2I3. 所以△O1O2O3 ≌ △I1I2I3. 解答此题的关键是发现△ADF，△DBE，△FEC之间的平移关系，注意到了这一点，此题就可以非常简捷的得到解决. 此题可以让学生感受到图形结构分析的重要性和从图形的变化的视角解决问题的优越性.

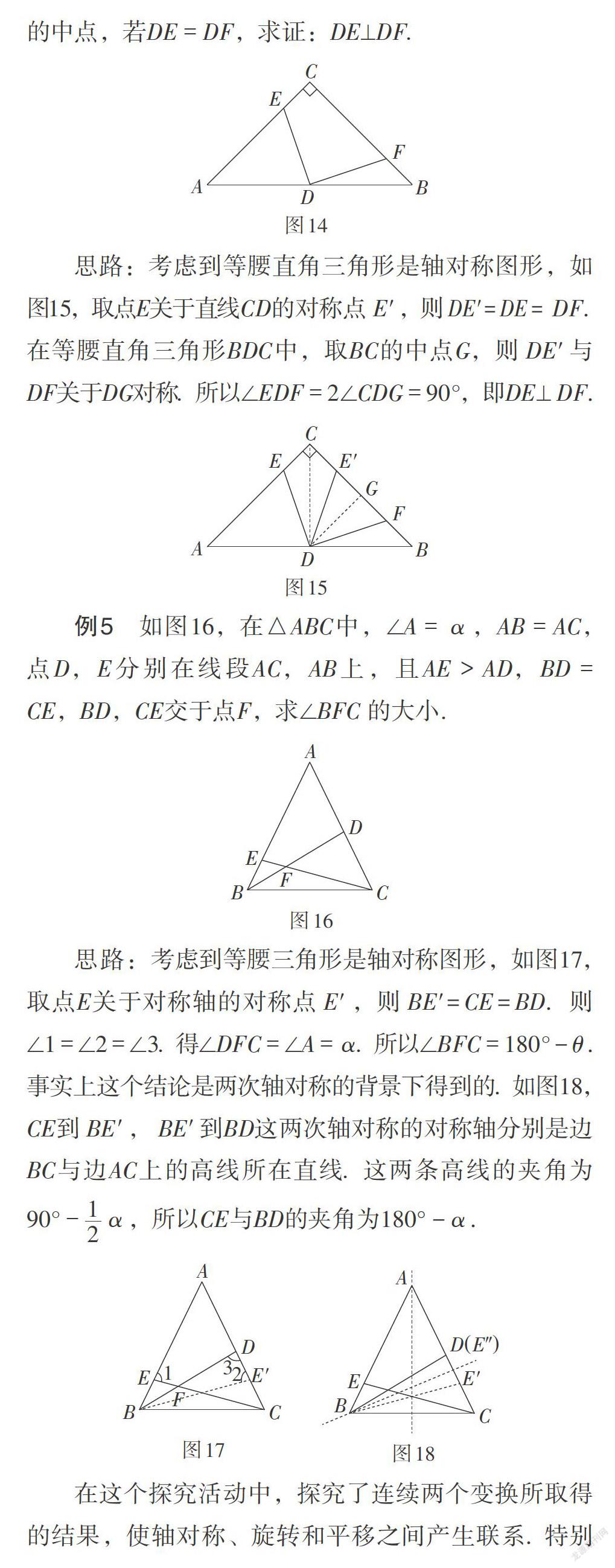
例7  如图24，已知点A到直线l的距离AD =[43]，点B在直线l上，以AB为边作等边三角形ABC. 当点B在直线l上运动时，求DC的最小值.

例7的探究过程的要点阐述如下.

学生开始会有一些猜测. 例如，BC与直线l重合时，DC取得最小值;点B与点D重合时，DC取得最小值，等等. 通过几何画板软件演示验证发现这些都不正確. 学生遇到了困难，教师可以引导学生思考，由于点D是定点，点C是动点，求DC的最小值，关键是弄清楚点C的运动轨迹. 在这样的启发下，学生开始关注点C的运动轨迹，通过描点发现点C的运动轨迹是一条直线，学生会想不通，为什么点C的运动轨迹是一条直线？有学生猜测，点C的运动是由点B的运动引发的，而点B的运动轨迹为直线导致了点C的运动轨迹也是直线. 教师可以再从另一方面来验证这种猜测，利用几何画板软件演示如果点B在圆上运动，发现点C的运动轨迹也是一个圆. 学生就陷入了深思，为什么点C的运动轨迹是由点B的运动轨迹决定的？至此，教师再引导学生观察点C和点B的关系，题目中给出的条件“△ABC是等边三角形”，即点B绕点A旋转60°得到点C，这是在旋转变换下的一对对应点.

为了更好地理解它们运动轨迹的关系，可以回到平移、旋转和轴对称的基本图形进行研究. 如图25，在一个平移下，对应点A和[A]的运动轨迹相同（图中虚线），它们的轨迹也有相同的平移关系;如图26，在一个旋转下，对应点B和[B]的运动轨迹相同（图中虚线），它们的轨迹也有相同的旋转关系. 再回到例7中，则例7变得简单，点C的轨迹是直线l绕点A旋转60°得到的直线[l]，DC的最小值即点D到直线[l]的距离[23].

在此题的探究过程中，让学生进一步理解了等边三角形的结构——旋转，更深入的理解了图形变化的性质——在平移、旋转和轴对称这样的变换下，对应点的轨迹是一样的.

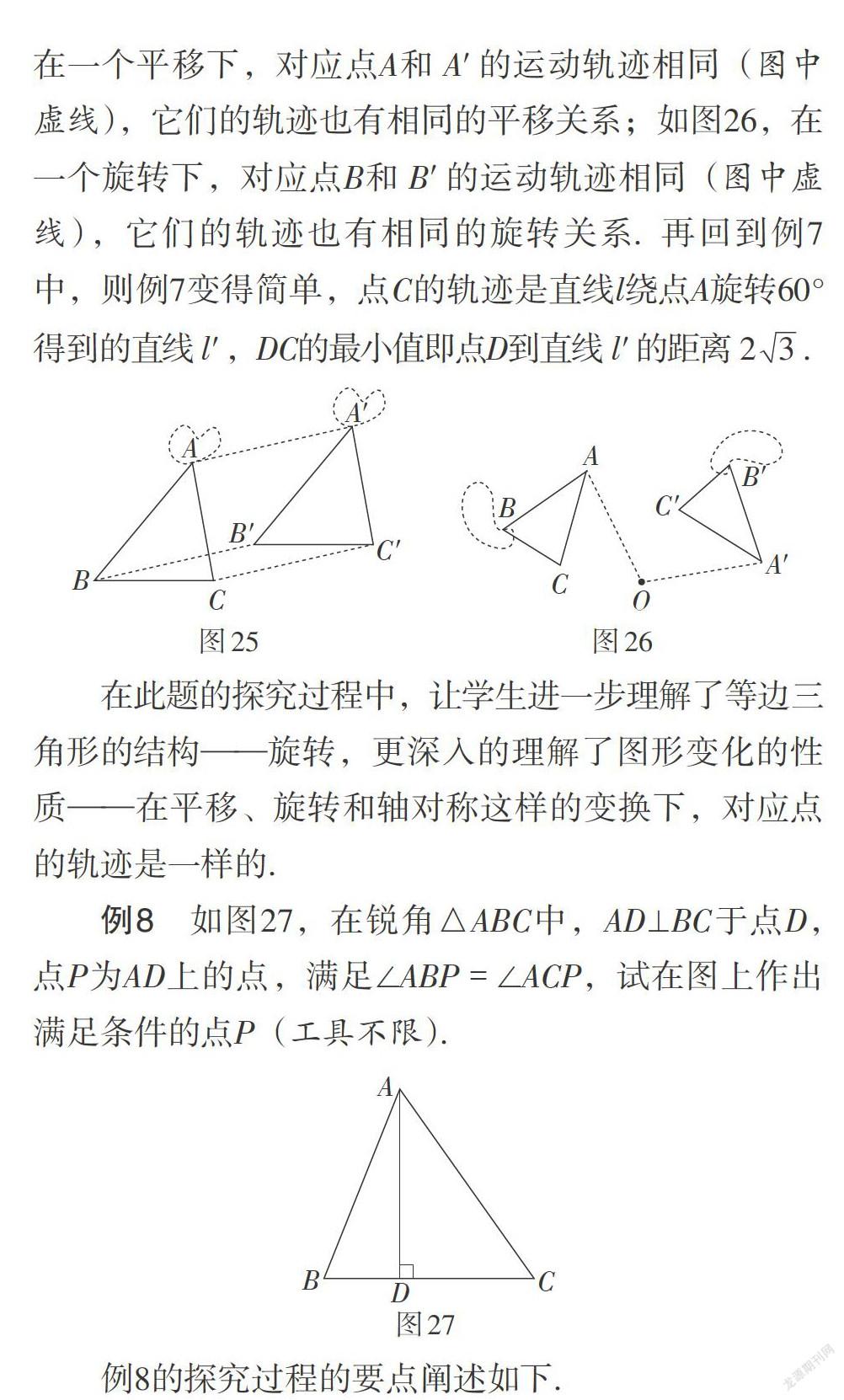
例8  如图27，在锐角△ABC中，AD⊥BC于点D，点P为AD上的点，满足∠ABP = ∠ACP，试在图上作出满足条件的点P（工具不限）.

例8的探究过程的要点阐述如下.

在这个题目的探究中，学生容易想到用轴对称变换，将AD左边的[∠ABD]轴对称到AD右边. 取点B关于AD的对称点[B]，则∠ABP = [∠ABP] = ∠ACP. 则点P在[△ABC]的外接圆上. 所以只要作[△ABC]的外接圆与AD的交点就是所求作的点P. 此时，例8看似解决得很完美，但前面的考虑要在BD[≠]CD的情况下. 当BD = CD时，AD上任意一点都符合题意. 另外，当BD [≠] CD时，由A，C，[B，] P四点共圆. 得[∠ACB =][∠DPB =]∠DPB.由[AD⊥BC，] 得[BP⊥AC.] 这样找点P不需要作[△ABC]的外接圆，只要作边AC上的高线，两条高线的交点就是所求作的点P. 此题需要分类讨论，轴对称变换，最后还能惊奇地发现，当BD[≠] CD时，所求作的点P就是[△ABC]垂心. 在这个过程中，还能发现过三角形的垂心及其任意两个顶点所作的三个圆相等. 整个探究活动不仅解决了问题，而且还发现了新的结论，将探究活动引向创新.

【设计意图】提供若干新情境的问题，引导学生从图形变化的角度解决，增强学生以图形的变化视角解决问题的意识，感受以图形的变化的视角解决问题带来的简便和对问题的本质理解，能在分析图形结构的基础上来选择相应的变换解决问题.

四、教学反思

在教学中，要让学生体验变换思想在几何问题解决中发挥的神奇作用，以简驭繁、揭示本质. 教学实践中，发现学生缺乏对变换思想运用的意识，这需要教师在教学中逐步渗透，需要引导学生从变换的视角观察图形的形成过程、图形的结构和图形的性质，也需要对图形变化的概念和性质从整体上进行更深入的理解.

在教学中，教师要规划单元整体设计，数学单元教学设计正是从整体功能出发，从更高观点对数学教学中的各要素进行系统的综合考量，使其产生整体效益. 系列探究活动的设计是单元整体性教学设计的核心，其实施为学生构建了前后一致和逻辑连贯的学习过程;系列探究活动的设计是基于对知识的系统理解，强调知识的关联和整合，使分散、零碎的学习内容变为一个有机的整体，从而能够使学生认识到学习内容的本质. 系列探究活动的实施强调学生主动参与，在活动中类比发现和形成知识结构，并能将探究过程中积累的经验迁移到新的问题情境，解决有挑战性的问题，实现深度学习. 学生经历上述系列探究活动，不仅能获得相关活动经验，而且能提升数学学科核心素养.

参考文献：

[1]萧振纲. 几何变换与几何证题[M]. 哈尔滨：哈尔滨工业大学出版社，2010.

[2]章建跃. 数学教学目标再思考[J]. 中国数学教育（高中版），2012（9）：2-4，7.

[3]吕世虎，杨婷，吴振英. 数学单元教学设计的内涵、特征以及基本操作步骤[J]. 当代教育与文化，2016，8（4）：41-46.