受环境扰动的随机SIRS 传染病模型的动力学分析

何雪晴，韦煜明

（广西师范大学 数学与统计学院，广西 桂林 541000）

很多学者不断建立数学模型来探究传染病的传播动力学行为[1-2]。1927 年，Kermack 等[3]首次提出并研究了SIR 模型，但这种模型只可用于具有永久性免疫力的传染病，而对于那些只具有暂时性免疫力的传染病通常用SIRS 模型来模拟[4-6]。

1 预备知识

如果在这些模型的基础上再考虑疾病的传播受到环境随机因素的影响，将更具有现实意义。例如，讨论受环境扰动的随机SIRS 模型[7-11]，研究传染病中的死亡率被环境扰动的影响[12]。本文基于文献[13-14]的研究，考虑了环境扰动对疾病接触率的影响，由此建立如下随机SIRS 传染病模型

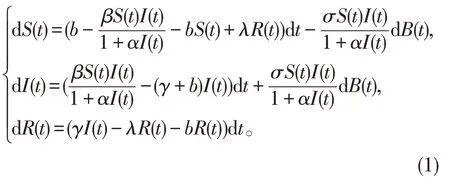
其中：S(t)表示t时刻的易感者；I(t)表示感染者，R(t)表示恢复者；b是S(t)的输入速率，令它等于人口的自然死亡率；λ为免疫丧失率；β为S(t)与I(t)间的接触率；γ为恢复率。(1)的确定性形式为

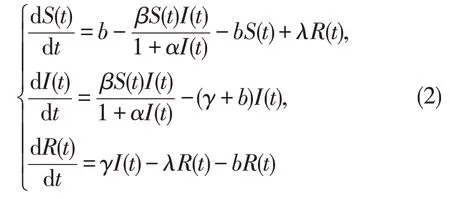
根据文献[15-17]中的计算方法可得模型(2)的基本再生数为R0=。若R0＜1，模型(2)唯一的无病平衡点E0=(S0,0,0)=(1,0,0)全局渐近稳定；若R0＞1，模型(2)唯一的地方病平衡点E*=(S*,I*,R*)也是全局渐近稳定的，其中

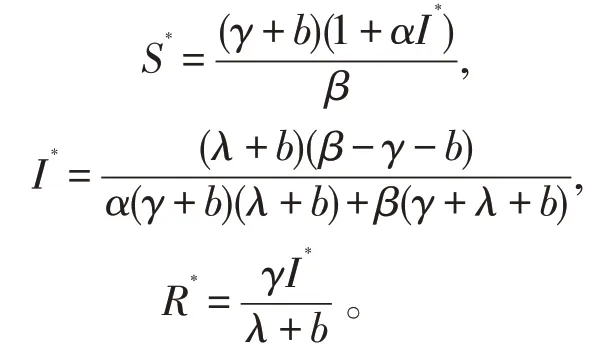
设(Ω,F,{Ft}t≥0,P) 是完备的概率空间，其中{Ft}t≥0是F上的滤子，它是右连续的且包含所有的P零测集，B(t) 被定义在该空间上，设∈Rn:xi＞0,1 ≤i≤n}。对n维随机微分等式

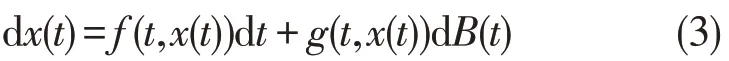
其中：f(t,x(t))是定义在Rn上的一个函数；g(t,x(t))是n×m的矩阵，f和g满足局部Lipschitz 条件；B(t)是m维的标准Brown 运动。(3)式的微分算子被定义为如下形式[18]

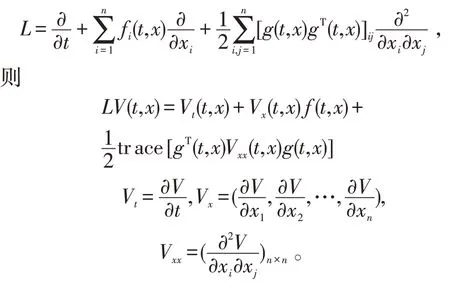
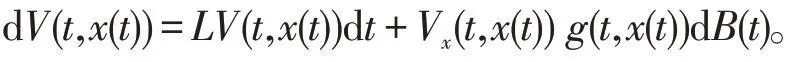
2 全局正解的存在唯一性

定理1对∀(S(0),I(0),R(0))∈，模型(1)在t∈[0,+∞)内存在唯一的正解(S(t),I(t),R(t))，且此正解依概率1 停留在，即 当t∈[0,+∞)时，(S(t),I(t),R(t))∈a.s.（几乎必然成立）。

证明由于模型(1)的系数满足局部Lipschitz条件，故对∀(S(0),I(0),R(0))∈，当t∈[)0,τe时，有唯一的正局部解，τe是爆破时间，下证此解是全局的，只需证τe=+∞a.s.即可。令k0≥1 充分大，使得S(0),I(0),R(0)∈对∀k≥k0，定义停时

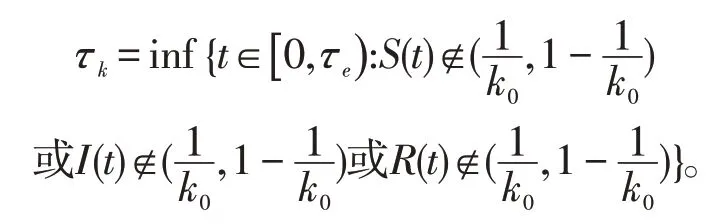
由(1)，对t∈[0,τk)有dR(t)＞-(λ+b)R(t)dt，

从而R(t)＞R(0)e-(λ+b)t＞0,∀t∈[0,τk)。

由于N(t)=S(t)+I(t)+R(t)满足等式dN(t)=0，则可令N(t)=1，所以对∀t∈[0,τk)，有

当k→+∞时，τk递增。令τ∞=，则τ∞≤τea.s.。若τ∞=+∞a.s.成立，则τe=+∞a.s.，且t≥0,(S(t),I(t),R(t))∈a.s.，故要证全局正解的存在唯一性，需证τ∞=+∞a.s.。利用反证法，假设不成立，则存在一对常数T≥0 和ε∈(0,1)，使得ε≤P{τ∞≤T}，所以存在整数k1≥k0，使得

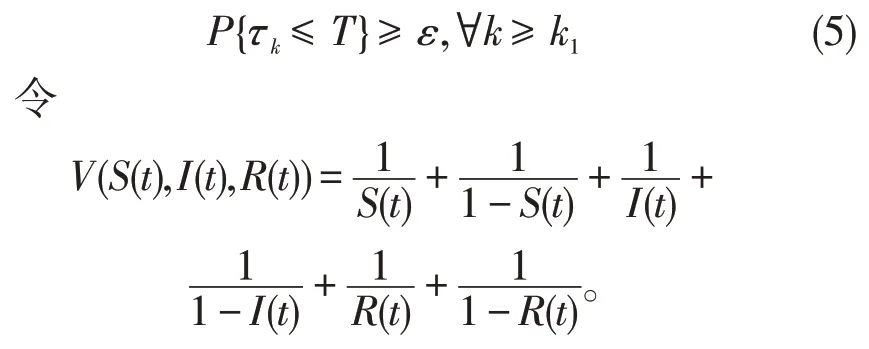
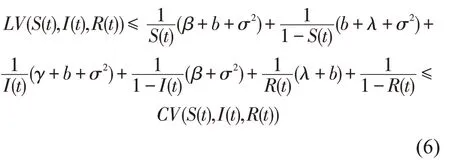
其中C=β+b+λ+γ+σ2。又因为

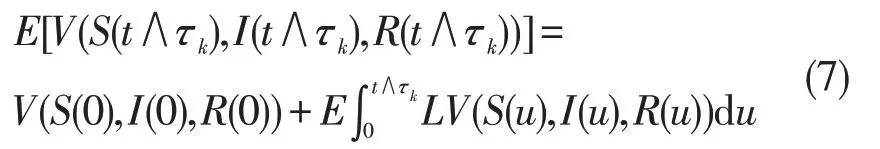
将(6)式代入(7)式有

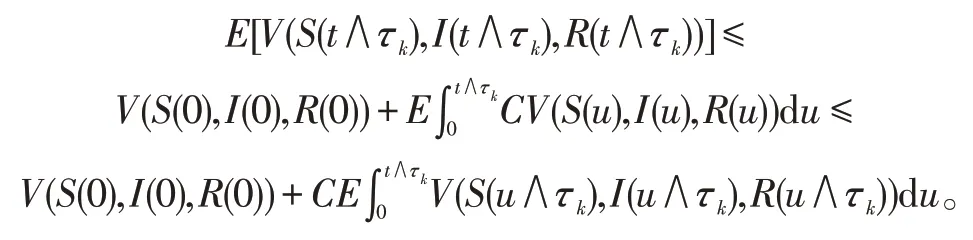
由Gronwall 不等式，令t=T，则

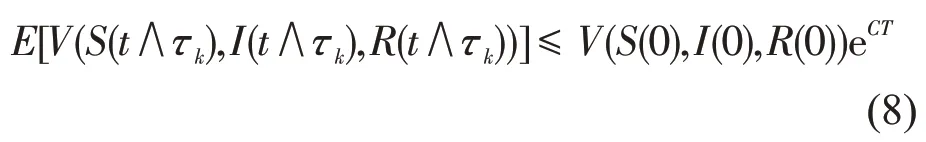
令Ωk={τk≤T}，由(5) 知，对 ∀k≥k1,P(Ωk)≥ε，再由(4)知

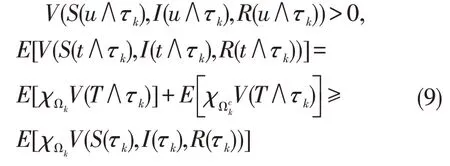
其中：χΩk是Ωk的示性函数。由停时定义，∀ω∈Ωk,S(τk,ω),I(τk,ω),R(τk,ω)至少有一个等于或，故

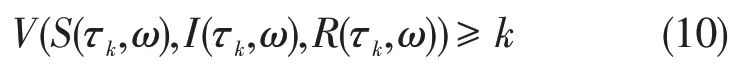
由(8)～(10)知

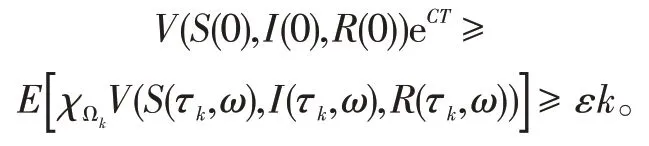
令k→∞，则有∞＞V(S(0),I(0),R(0))eCT=∞。

显然矛盾。故定理得证。

3 疾病的灭绝性

定理2设S(t),I(t),R(t) 是系统(1)初始值为(S(0),I(0),R(0))∈的解，有

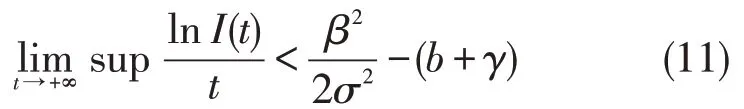
引理1[19]设M(t):t≥0 是局部连续鞅，M(0)=0，令δ＞1，γn和τn为正项序列，则对几乎所有ω∈Ω，∃n0=n0(ω)为正整数，当对∀n≥n0有

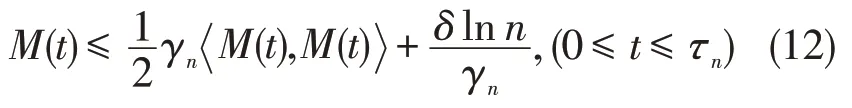
证明由公式以及(1)式知

对∀n-1 ≥t≥n，对(15)式两边除以t得

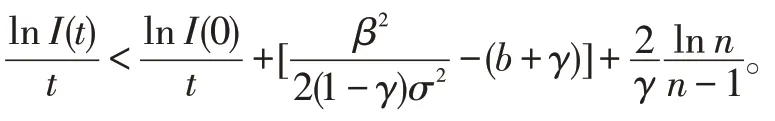
令n→+∞，则t→+∞,再令γ→0，则

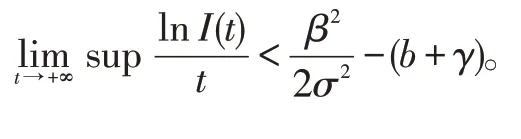
4 疾病在均值意义下的持久性

定义1若，则疾病在均值意义下是持久的[19]。

由定义1 易知疾病在均值意义下是持久的。

5 数值模拟

下面给出不同的参数值，进行数值模拟来说明本文定理结论的正确性。首先利用Milstein 方法[20]将模型(1)离散化

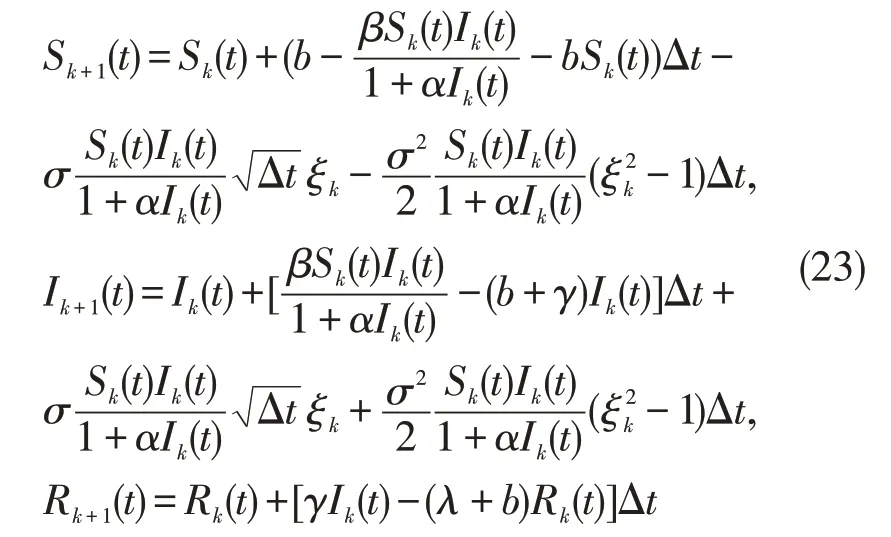
其中ξk,k=1,2,…,n是独立的高斯随机变量，给定初始值(S(0),I(0),R(0))=(0.7,0.2,0.1)。

(1)当σ=0 时，系统(23)变为

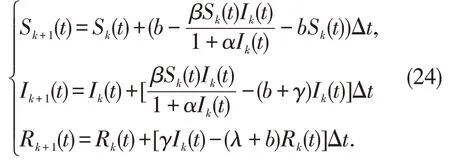
此时传染病不受外界环境干扰，若取β=0.4,b=0.15,λ=0.012,α=0.2,γ=0.35，则R0=0.8 ＜1，无病平衡点E0=(1,0,0)是全局渐进稳定的，传染病随时间的流逝慢慢就会消失，如图1；若取β=0.4,b=0.15,λ=0.012,α=0.2,γ=0.05，则R0==2 ＞1，地方病平衡点E*=(S*,I*,R*)是全局渐近稳定的，也就是说传染病会传播并持续存在，如图2。(2)σ≠0 时，传染病将会受外界环境干扰，如政府或者医疗部门干预、媒体报道等，若β=0.4,b=0.15,λ=0.012,α=0.2,γ=0.35,σ=0.25，则满足＜(b+γ)。模型(1)解的轨迹会在无病平衡点E0=(1,0,0)周围波动，且t不断增大时，疾病将以概率1灭绝，如图3。若β=0.4,b=0.1,λ=0.012,α=0.2,γ=0.05,σ=0.2，则～R≈5.067 ＞1，模型(1)解的轨迹如图4 所示，当t的不断增大，疾病I(t)在均值意义下是持久的，并且它会围绕地方病平衡点E*=(S*,I*,R*)上下波动。

图1 σ=0 时模型(2)的无病平衡点全局渐进稳定

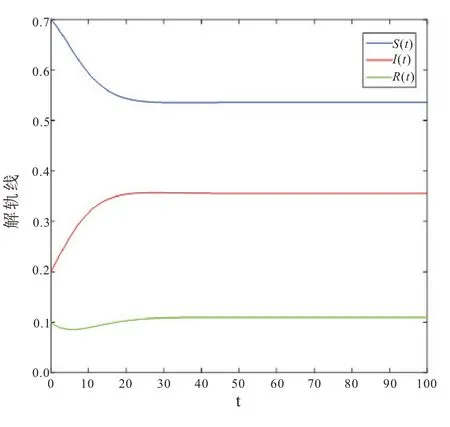
图2 σ=0 时模型(2)的地方病平衡点全局渐进稳定

图3 σ ≠0 时模型(1)疾病以概率1 灭绝

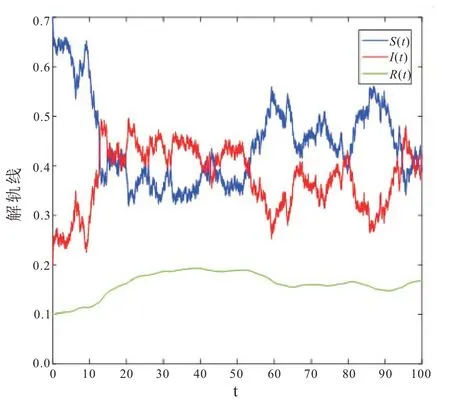
图4 σ ≠0 时模型(1)疾病在均值意义下的持久性

可以发现，受到环境扰动的随机模型(1)与不受到任何环境扰动的确定性模型(2)相比，模型(1)传染病的灭绝条件要比模型(2)传染病灭绝的条件弱，由于现实生活中的传染病会难以避免的受到环境的随机干扰，所以本文考虑环境对接触率的扰动具有实际意义。

6 小结

首先证明随机模型全局正解的存在唯一性，然后讨论疾病的灭绝与持久性，如果满足＜(b+γ)，则疾病是依概率1 以指数形式趋于灭绝的，如果＞1,则疾病在均值意义下是持久的，所以据此能够更好的预测和防控疾病的流行和灭绝。另外，根据R0的表达式可以看出，研发高效的传染病疫苗对患者进行接种，使得恢复率提高，患者减少，所以接下来研究具有接种的传染病模型也具有重要的现实意义。