基于结构?整体着力


[摘要] 以喻平教授CPFS结构为理论依据,整体设计一元一次不等式(组)的复习,在目标引领下,“唤醒—应用—综合—引申—小结”等五环节环环相扣,零散的知识在聚合中整体发力,在不等式域完善中应用,在应用中转知成识,让复习更富有价值。
[关键词] 一元一次不等式(组);复习设计;CPFS结构;整体教学
一元一次不等式(组)是在七年级下册(人教版)学过的内容,学生已经经历了新授课的学习,在后续函数、二次根式、一元二次方程等知识中也得到过初步的应用,但总体而言还是零散的、粗浅的,没有形成前后知识的内在关联,没有构建学生良好的CPFS结构。对初三的中考复习来说,有了两年多的数学学习经历,学生已具备了一定的学习能力与探索意识,不论是面对中考,还是面对自己的进一步发展,对初中数学的总体把握也有了较为迫切的需要,这样外力与内在的共同作用力,加上喻平教授的CPFS结构的宏观引领,为课堂的成功奠定了理论基础和心理基础。
一、设计说明
(一)本复习课的理论支撑
喻平教授等提出:一个数学概念C的所有等价定义的图式,叫作概念C的概念域。一组具有数学抽象关系的概念网络的图式叫作概念系。与命题A等价的命题集的图式叫作命题A的命题域。在一个命题集中,其中任意一个命题都至少与其他某一个命题有“推出”关系,就称这个命题集的图式为一个命题系。概念域、概念系、命题域、命题系(记为CPFS结构)是对数学认知结构的精确描述,它反映了数学学习特有的心理现象和规律。CPFS结构理论准确地刻画了数学知识在个体头脑中的组织形式,它是一种优良的数学认知结构,而奥苏伯尔认为优良的认知结构有助于迁移。故此可推知,学生的CPFS结构的形成是学生深度理解数学的表征,是学生学力、思维力强的一种体现,它为复习教学结构化、系统化思维路径提供了理论上的依据。
(二)整体教学构想
“任何知识总处于联系之中,时间上处于历史的联系中,空间上处于结构的联系中。……如果教师把所传授的知识置入过程和联系之中,课堂里的知识空间就自然形成了。”基于这样的认识,本复习课以一个母题为基,以题唤知,通过题目的串并联、优化组合,把题目的潜能挖掘出来,充分发挥题目的唤醒与贯通作用,题尽所能,整个设计充分利用了母题资源,既减低了重复计算所带来的外部认知负荷,又贯通了知识的内在联系,凸显出数学之本质。依次通过数学活动,引导学生领悟知识的纵向联系和横向联系、直接联系(显性联系)和间接联系(隐性联系),让学生既见树木又见森林,意在促进对知识的整体建构。这种立足CPFS结构下的系统统摄力的复习,将使得知識更具张力,更具应用性和迁移力,在应用中见证价值,在实践中深化理论,进一步感知不等式(组)复习的必要性、不可或缺性。
基于以上整体构想和理论支撑,设计了本节复习课。
二、复习目标
《义务教育数学课程标准(2011年版)》对“不等式与不等式组”目标提出要求:结合具体问题,了解不等式的意义,探索不等式的基本性质;能解数字系数的一元一次不等式并能在数轴上表示出解集,会用数轴确定由两个一元一次不等式组成的不等式组的解集;能根据具体问题中的数量关系,列出一元一次不等式,解决简单的问题。基于此,立足知识前后关联的整体观,基于课标的定位,结合近年来全国各地中考试卷中关于不等式(组)题目的特点,确定如下复习目标:(1)通过题组的唤醒与再现,梳理出本章的知识结构,进一步掌握不等式的性质,会运用它熟练地解一元一次不等式(组),并能通过数轴表示其解集;(2)基于CPFS结构理论,通过应用题组展现不等式的广泛应用性,完善不等式的应用域,增进对不等式的积极体验,加深对其复习必要性的认识;(3)认识不等式与方程、函数等领域的关联,通过这种关联加深对建模思想、数形结合思想、分类讨论思想的认识,进一步落实化归。
三、复习流程
环节1 唤醒中再现
(1)下列5个式子:①-3<0;②2x+5y>0;③x-2=0;④2(x+2)>3x;⑤≤-1;属于
一元一次不等式的是______.(填序号)
若a>b,则:①a-2______ b-2;②2a ______ 2b;
③ ;④ ac2 ______ bc2.(填不等号)
(2)解不等式⑤,并把解集表示在数轴上。
(3)解④、⑤组成的不等式组,并确定其整数解。
跟进思考:同学们以(3)中的两个不等式为基,还能改编出不同于(3)中的不等式组并求其解集吗?
路径预设:改换不等号方向即可改编为新题,进而求其解集。
[设计意图]设置具有内在关联性的三个小题目是不等式知识体系中最基础、最本质的内容,也是最重要、最核心的内容,以此构成了本专题复习的认知起点。其中,不等式的基本性质是不等式解法的基础和依据,是不等式与不等式组的重要支撑。另外,在中考中相关不等式性质本身的考查也时有出现,而不等式(组)的解法是本部分最基本、最核心的方法,是进一步用之解答问题的基本保障。通过设计这三个简单的小题,唤醒知识、梳理知识,通过学生的解答情况来落实以学定教,为后续学习提供先手材料。
基于三个问题的顺序性、关联性,具体教学时,利用PPT,要把所设计的三个小问题依次呈现,而不可一次性直接呈现出来(若一次性呈现体现不出问题的生成性和递进性)。问题1是为了回顾一元一次不等式的概念及不等式性质;问题2是为了回顾解不等式的基本技能及解集的数形结合表达;问题3指向不等式组的解法技能及其整数解问题,且问题2、3均选材于问题1这一母题,从经济、智能两个角度充分利用了母题资源,使其具有内在的关联性。然后通过跟进思考这一环节,使得不等式组解集的四种情形(取大、取小、取中间、无处取)全程展现,形成知识的整体缩影。如此处理,既减少了重复解不等式,节省了复习时间(经济),又通过这种优化的变式,调节学生的复习兴趣与热情(智能)。可以看到,这些题目均基础题,但基础中孕育着创新,践行了张奠宙教授“让基础富有灵性”的观点。
环节2 应用见关联
(1)三角形三边长分别为4,1-2a,7,则a的取值范围是______ .
(2)二次根式在实数内的取值范围是______ .
(3)已知:在钝角三角形中,一个锐角是另一个锐角的2倍,则较小的锐角的度数范围是 ______ .
(4)点A(m,m-3)在第4象限,则m的取值范围是______ .
(5)一次函數y=(m+2)x+1,若y随x的增大而增大,则m的取值范围是______ .
(6)若关于x的方程x2-4x+m=0没有实数根,则实数m的取值范围是______ .
(7)若抛物线y=(3-m)x2-4x+m的开口向下,则m的取值范围是______.
(8)若直线y=(m-2)x+1与双曲线 没有公共点,则m的取值范围是 ______ .
(9)若抛物线y=ax2+2x+3与x轴有两个公共点,则a的取值范围是 ______ .
[设计意图]基于三角形的三边关系、分式或根式的取值范围、三角形三个角的制约关系、平面直角坐标系内点的象限符号特征、一次函数的增减性、一元二次方程根的存在情况、抛物线的开口方向、图像的公共点问题、抛物线与坐标轴的公共点等问题设计了9道计算量相对较小的小题目,基本上把初中学段相关不等式(组)应用的知识点来了个盘点,彰显了不等式(组)的应用价值,打通了不等式的纵横关联,将知识的学有所用、学有所值凸现出来,有利于不等式(组)“应用域”的集成与完善。这类基于数学内部单项关联的题组,既体现了不等式在数学内部的广泛应用,又唤醒了邻近知识,加固了知识的整体化体系。
教学时可以利用PPT一次性呈现出来,以中等生完成为节点进行不等式应用范畴的梳理,安排学优生在提前完成填空的基础上帮扶学困生;通过先行梳理这一数学认知结构,让学生想一想,初中学段还有哪些领域会用到不等式(组)。如此兼顾多个层级,力争实现每个人在各自基础上的不同提高。
环节3 综合中联通
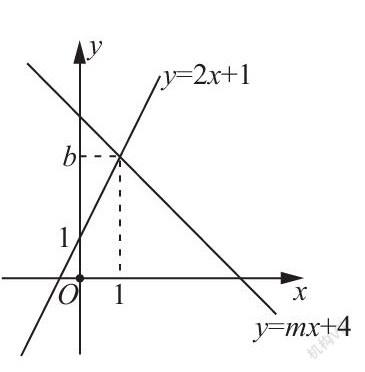
如右图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值.
(2)写出不等式2x+1 (3)垂直于x轴的直线x=a与直线l1、l2分别相交于C、D,若线段CD长为2,求a的值. [设计意图]这是一道把方程、不等式、函数链接在一起,打通其内在关联的小综合题目,它以数形结合的形态,系列呈现,有机地融合在一起,见证了不等式在代数领域内的结构体系,是对环节2的一种综合性体现,也是基于复习的整体性、关联性开发而设计的。其中的(1)是在函数图像的背景下,以公共点为依托,连通共同点的坐标与方程的解,通过解一次方程确定出两个待定字母;问题2是借助几何直观,直接观察出不等式的解集,是数形结合思想的展现,当然也可以通过解不等式组去完成,但如此就走了个弯路;问题3是以函数为载体,通过特殊状态下两点之间的距离构造出绝对值方程,进而转化为两个一元一次方程而获解。 教学时,可以先行展示图片,让学生观察并提问:能得出什么结论?以此图像能具体确定什么?题目的问题会怎样设计?然后再呈现题干条件,依次把三个问题摆出来。这样学生会在比对自己设定的问题中获得自信或形成新的认识,感觉中考题无非如此。接下来让学生先尝试解答,再通过同位交流、小组交流、全班交流等不同形式完成这一题目的教学,让学生进一步体悟到方程、不等式、函数的联系,促进大整体观的形成。 环节4 引申中拓展 (1)用三个不等式a>b,ab>0,<中的两个 不等式作为题设,余下的一个不等式作为结论组成一个命题,组成真命题的个数为( ). (A)0(B)1 (C)2(D)3 教学说明:本题取自2019年北京市中考题,是对不等式性质2的改造。根据不等式性质2:若a>b,c> 0,则ac>bc(或>)。以上试题把其中的“c”替换成了“ab”,那么不等式>自然变成了>, 简化得 > ,即<。这样,题设中的三个不等式 显现出来。但本题并未如此进行直接考查,而是把两个条件和一个结论的三个不等式平行给出,然后以两个不等式作为题设,余下的不等式作结论重组命题,并判断命题的真伪,这就增大了题目的挑战性和可变性,成为一道根植教材的创新题。通过本题能够进一步提升对不等式性质的理解,以及多视角、辟蹊径的联想意识。当然,不管用什么方法解题,首先要构造命题: ①若a>b,ab>0,则<; ②若ab>0,<,则a>b; ③若a>b,<,则ab>0. 预设法一:用不等式性质,这应该是最容易想到的思路。 预设法二:作差比较法。这也是解不等式问题常用的方法。 预设法三:构造函数。借助外观特征<,若有 构造函数的意识,其实不难联想到反比例函数y=,当 自变量的值分别a、b时,对应的函数值即为、。如此, 它们的大小自然和函数的增减变化趋势挂起钩来。 (2)若关于x的不等式组有解,求a 的取值范围;若无解呢?若只有两个整数解呢? [设计意图]本题反其道而行之,不是给出具体不等式组去求解(集),而是知道有解、无解、有怎样的解,欲反求待定字母的取值或取值范围。这种逆向问题,挑战的是学生的逆向思维,指向的是深度学习、深度思维。本题从构成上,仍然充分利用了母题中的不等式④和⑤,把④中不等式左端的x变为待定字母a,不等式⑤不变,两个不等式结合而成含待定字母的不等式组,然后就可以递次设计出三个问题,其中“有解”与“无解”是互补的,有解解决了,无解随之而定;而“只有两个整数解”对学生颇有冲击力,是个难点,在此集中体现意在循阶而上,处理起来相对顺畅,能充分利用已经启动起来的思维和解题资源,体现了有关不等式求解的整体性。 具体教学时,首先鼓励学生尝试解答,在发现共性问题时再组织交流,其中可以借力于数轴工具去探索,以感知数形结合的魅力。本拓展环节的两个问题,从深度学习的定调出发,把不等式性质的应用及不等式解集问题引向深入,一个发散思维、一个逆向思维,均是创新思维的践行,核心素养嵌于其中。“引领学生思维生成、思辨、归纳、延伸,开拓思维角度,提升思维高度,挖掘思维深度,开拓思维宽度,优化思维品质,让教学实践成为思维活动的再现,让知识成为思维活动的结果”,整个环节注重基本知识的理解、基本思想本质的挖掘、变式应用的把握,呈现出深度思维的复习课样态。 环节5 小结筑结构 通过前面四个教学环节,渐次生长形成以上内在知识结构,帮助学生构筑各自的认知结构,逐步完善其不等式应用域的CPFS结构体系,以增强知识整体化所产生的“造血功能”。 四、结语 借力喻平教授的CPFS结构,设计了“再现—应用—综合—引申—小结”五个教学环节,意在形成不等式(组)应用域体系。这样复习,使得原本零散的知识聚合在了一起,变“惰性知识”为活性知识,成为具有良好迁移力的知识。实践见证了笔者的认识,收获了优质的复习效果。需要说明的是,为了突出不等式在数学内部应用的本体结构,本设计没有涉及不等式在现实生活中的应用,建议把它与方程、函数在现实生活中的应用结合起来,更能体现常量模型和变量模型的关联性。 [本文系山东省教育教学研究重点课题“基于初中数学课程整合的单元教学案例研究”(项目编号:2020JXZ026)阶段性研究成果] [参考文献] [1]喻平,单墫.数学学习心理的CPFS结构理论[J].数学教育学报,2003,12(1):13-16. [2]刘庆昌.课堂里的精神空间[J].当代教育与文化,2011,3(6):22-28. [3]程华.数学课堂思维教学若干问题的思考[J].数学通报,2018,57(3):26-29. 邢成云 山东省滨州市北镇中学初中部,正高级教师,山东省特级教师。“万人计划”全国教学名师,全国首期名师领航工程人选,山东省优秀教师,山东省有突出贡献的中青年专家。

