Hilbert空间中强半压缩算子迭代序列的误差估计及稳定性分析
范红磊, 王朝
(南京信息工程大学数学与统计学院,江苏 南京 210044)
1.引言及预备知识
设(H,〈.,.〉)是一实Hilbert空间, 具有诱导范数‖.‖,C为H的一个非空闭凸子集,T:C →C是一非线性算子,x0∈C是给定的初始点, 定义序列{xn}:
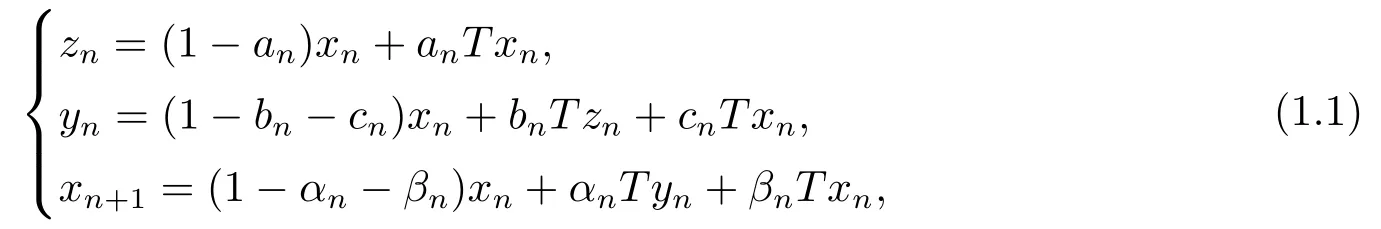
其中{an},{bn},{cn},{αn},{βn},{bn+cn},{αn+βn}⊂[0,1],n ≥0.若在(1.1)中取βn=cn=0,则(1.1)式被称为Noor迭代[1].若取βn=cn=an= 0, 则(1.1)式被称为Ishikawa迭代[2].若取βn=cn=an=bn= 0, 则(1.1)式被称为Mann迭代[3].2015年, Maruster和Maruster[4]根据半压缩算子的定义提出了强半压缩算子(SDC)的概念: 如果对于任意的x ∈C, 有
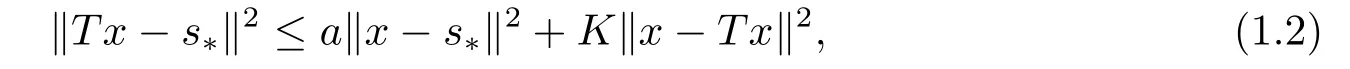
其中s∗∈Fix(T) ={x ∈C:Tx=∅(s∗称为T的不动点),a ∈(0,1),K ≥0, 则算子T被称为强半压缩算子(注意到若T是一强半压缩算子, 则其不动点是唯一的).在此基础上,文[4]研究了在强半压缩算子下的Mann迭代的误差估计和T-稳定性.WANG[5]改进了文[4]的结论, 得到了Mann迭代误差估计的一个新的公式, 与文[4]中误差估计式相比有更快的收敛速度, 并且根据所得误差估计式得到了迭代序列强收敛的一个充分条件.在文[6]中, WANG等对[4-5]进行了推广, 建立了Ishikawa迭代的两个误差估计式和强半压缩算子的强收敛定理, 并讨论了Ishikawa 迭代及Mann迭代的收敛速度和误差估计, 最后证明了Ishikawa迭代的T-稳定性.Grsoy等[7]在不同的条件下, 提出了Mann迭代的稳定性定理.与此同时, 文[7]中考虑了强半压缩算子下的Mann迭代的弱ω2-稳定性, 并讨论了强半压缩算子的数据依赖性.文[8-9]研究了Jungck-Khan迭代的强收敛性和T-稳定性, 并给出了Jungck-type迭代的数据依赖定理.
本文将讨论在强半压缩算子下的迭代序列(1.1)的误差估计及稳定性.首先, 给出在Lipschitz条件下该迭代序列的误差估计及强收敛的充分性条件, 并举例与文[6]中所得Ishikawa迭代的误差估计式进行对比.其次, 在非Lipschitz条件下, 我们也讨论了该迭代序列的误差估计式及强收敛的充分性条件.最后, 分析了该迭代序列的T-稳定性.所得结果推广了文[4-9]的相关结论.
为了证明本文的主要结果, 我们需要以下定义和结论.
定义1.1[10]设X是一实Banach空间,C为X的一个非空闭凸子集,T是C上的自映射,x0∈C为任意给定的点, 若由

生成的序列{xn}强收敛到T的不动点s∗∈Fix(T), 则称迭代序列(1.3)是T-稳定的(或关于T是稳定的)当且仅当对任意的序列{yn}⊂C, 有
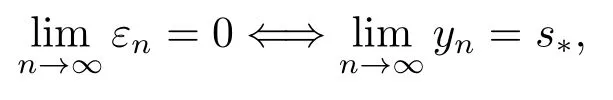
其中εn=‖yn+1−f(T,yn)‖.
引理1.1[10]设(H,‖.‖)是一实Hilbert空间, 对∀x,y ∈H, 有
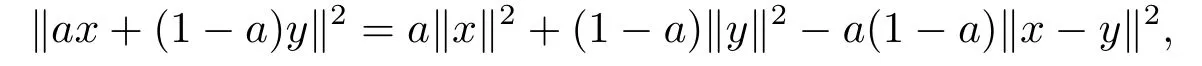
其中a是一实数.
引理1.2[11]设(H,‖.‖)是一实Hilbert空间, 则对于∀x,y,z ∈H, 有
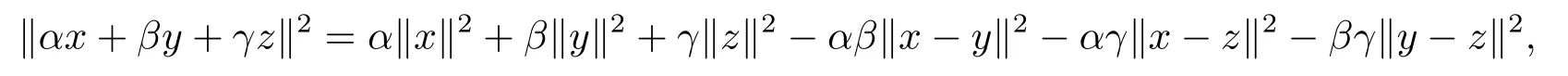
其中α,β,γ ∈[0,1],α+β+γ=1.
引理1.3[10]设{dn},{εn}是两个非负实数列, 满足
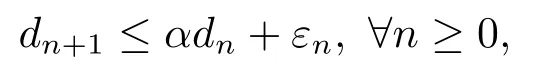
其中0≤α<1.若则
?
引理1.4[5]设{dn}是一非负实数列, 满足
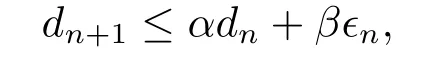
其中0<α<1,β >0.若{ϵn}是一非负实数列, 且满足


2.强半压缩算子的迭代序列(1.1)的误差估计
本节我们将给出强半压缩算子下的迭代序列(1.1)的两个误差估计式及相应的强收敛的充分性条件, 并举例与已有的误差估计式进行对比.
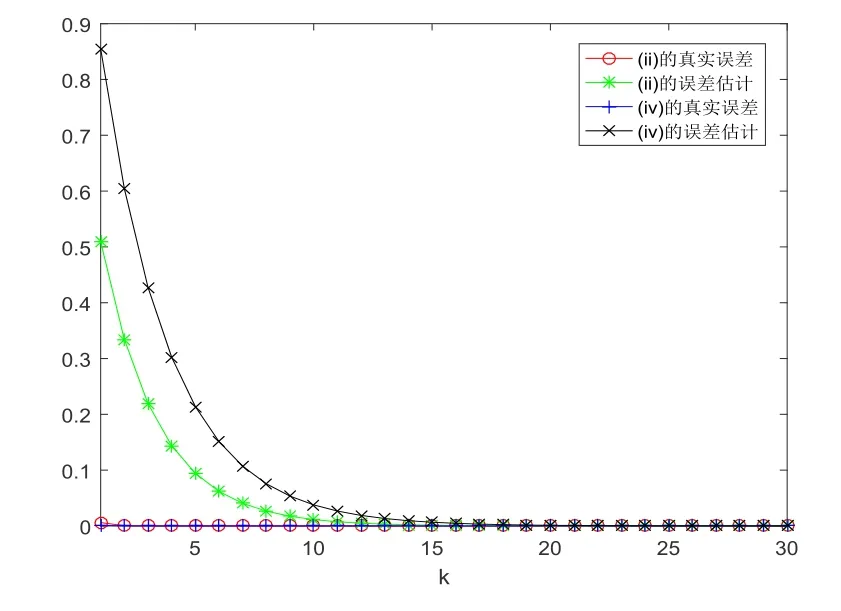
定理2.1设T是L-Lipschitz的(即对于∀x,y ∈C, 存在L, 使得‖Tx −Ty‖ ≤L‖x −y‖),且T是一强半压缩算子, 其中0 其中Tαn,βn,bn,cn,an:=(1−αn−βn)I+αnTbn,cn,an+βnT,Tbn,cn,an:=(1−bn−cn)I+bnTan+cnT,Tan:=(1−an)I+anT.设{xn}⊂C是由(1.1)产生的序列, 且满足 则有如下估计式: 证由引理1.2可得 因为T是一强半压缩算子, 故由(1.2)及引理1.1, 我们有 因为T是L-Lipschitz的, 所以 从而 将(2.3)-(2.6)代入到(2.2)中得 其中 此时(2.7)可转化为 与文[6]中定理2.2的证明过程相似, 我们有 注2.1上述定理推广了文[6]中定理2.2的相关结果. 注2.2与文[6]中类似, 当T为可微映射时, 条件(∗)是容易实现的.事实上, 若T是可微、Lipschitz的强半压缩算子, 且由迭代过程(1.1)产生的序列{xn}满足 则有 其中ξ=x+η(t2+t1t4+t1t3t5)(Tx −x),0<η <1.若T的导数T′满足 则 由定理2.1可知,{xn}强收敛于不动点s∗, 且满足误差估计式(2.1). 下面我们考虑文[6]中的例子, 将(1.1)和(2.1)与文[6]中Ishikawa迭代序列及误差估计式进行对比. 例2.1[6]设C=[0.5,1.5], 定义T:C →C: T是1-Lipschitz的且是强半压缩的(a=0.15,K=0.42), 其不动点s∗=1. 1)对于Ishikawa迭代.根据文[6]中定理2.2,因为0<θ1<θ2 我们有 因此 即满足文[6]中定理2.2的所有条件. 故 即满足定理2.1的所有条件. 下面我们比较Ishikawa迭代和迭代序列(1.1)的收敛速度和误差估计.分别取Ishikawa迭代序列中t1=0.8, t2=0.5和t1=0.9, t2=0.5.迭代序列(1.1)中t1=0.78, t2=0.19, t3=t4=t5= 0.4 和t1= 0.8, t2= 0.13, t3= 0.3, t4= 0.4, t5= 0.5.设终止参数为‖xn −s∗‖ ≤10−5.经过计算, 迭代次数和误差估计的结果分别在表2.1和图2.1中给出. 图2.1 初始值x0 =0.5的迭代序列(ii)、(iv)的真实误差‖xk −s∗‖(1 ≤k ≤30) 和误差估计 表2.1 Ishikawa迭代和迭代序列(1.1)收敛于s∗=1所需的迭代次数 注2.3从表2.1我们可以看出:1) (iii)和(iv)的收敛速度是稳定的; 2) (iv)比其他三个迭代收敛得更快.从图2.1可以看出(ii)的误差估计比(iv)的误差估计更有效.但当迭代次数k=30时, (ii)和(iv)的误差估计都达到了10−5, 此时我们认为误差估计的有效性是一致的. 定理2.2设T是一强半压缩算子, 其中0< a <1,K ∈[0,1),s∗∈Fix(T).假设存在0≤q,s<1 及正数θ1,θ2, 0<θ1<θ2 证由文[4]中定理2知 由条件M <1及引理1.2知 此时 从而 与定理2.1的证明过程相似, 我们有 注2.4上述定理推广了文[5]中定理2.1的相关结果. 注2.5与注2.2相似, 若T是可微的强半压缩算子, 且由迭代过程(1.1)产生的序列{xn}满足 时, 条件(∗)成立.由定理2.2知, 序列{xn}强收敛于不动点s∗, 且满足误差估计式(2.8). 我们考虑如下例子. 例2.2设C=[−1,1], 定义T:C →C如下 其不动点s∗= 0.此时T是一强半压缩算子(a= 0.008, K= 0.07).令q= 0.58,s= 0.25, 因此a+q <1.由0<θ1<θ2 故t1∈[0.6801,0.8859],t2∈[0,0.25](需要注意的是t1+t2≤1),t3+t4∈[0,0.58],t5∈[0,1].若t1∈[0.877,0.8859],t2∈[0.1119,0.1141],t3=0.28,t4=0.3,t5∈[0.59,0.6], 则有 即满足定理2.2的所有条件.我们可取t1=0.877, t2=0.114, t3=0.28, t4=0.3, t5=0.59, 所得迭代程序(1.1)的真实误差和误差估计(取迭代次数k= 60, 初始值x0= 0.6)可达到10−6, 故我们认为真实误差和误差估计的有效性是一致的. 则 将(3.2)及(3.3)代入到(3.1)中得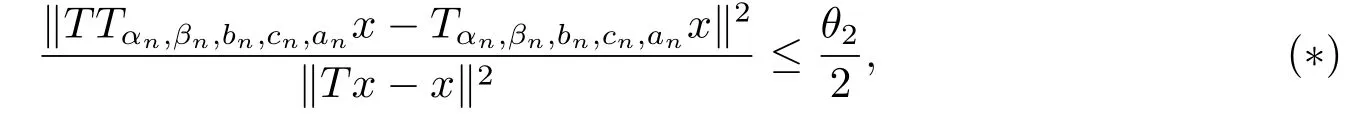
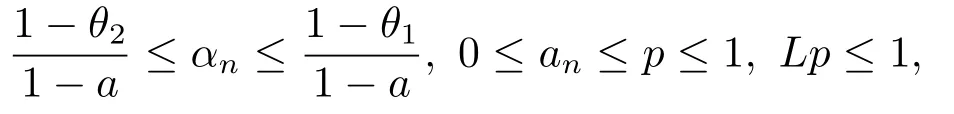
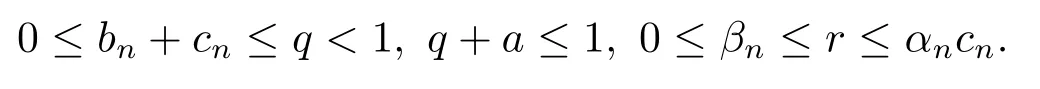
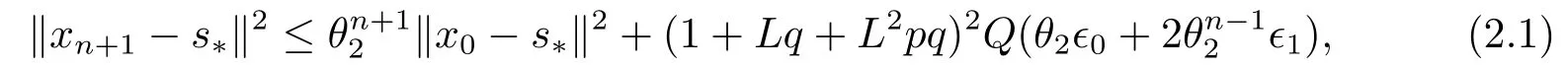
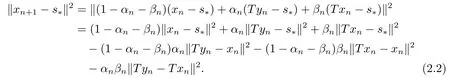
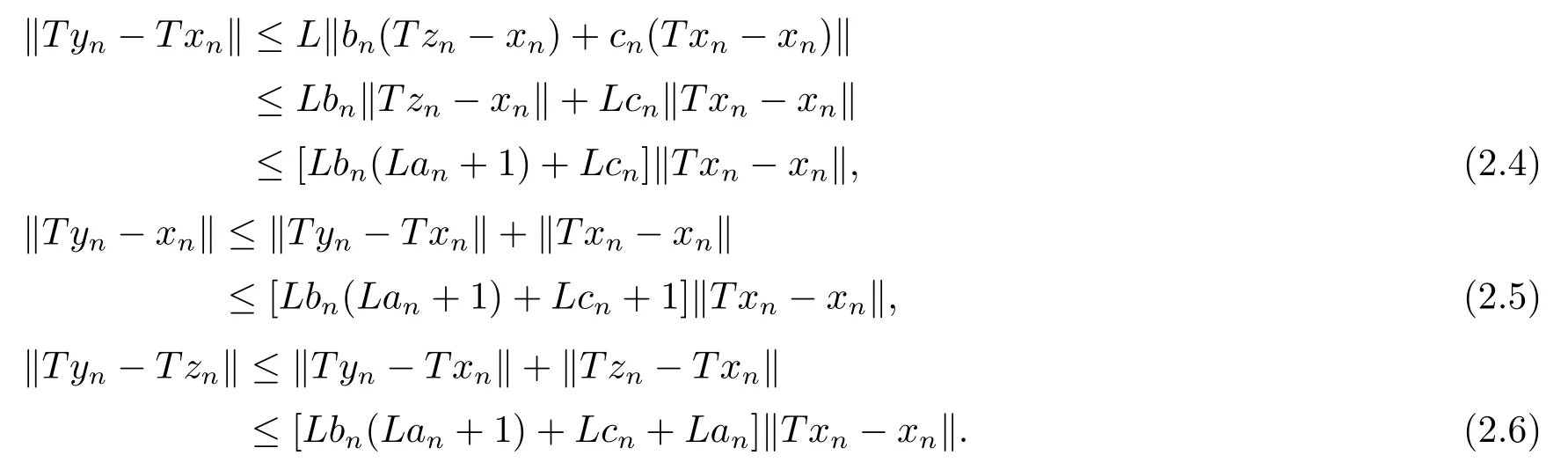
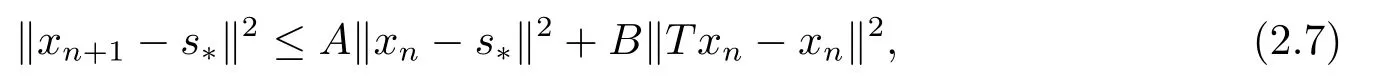
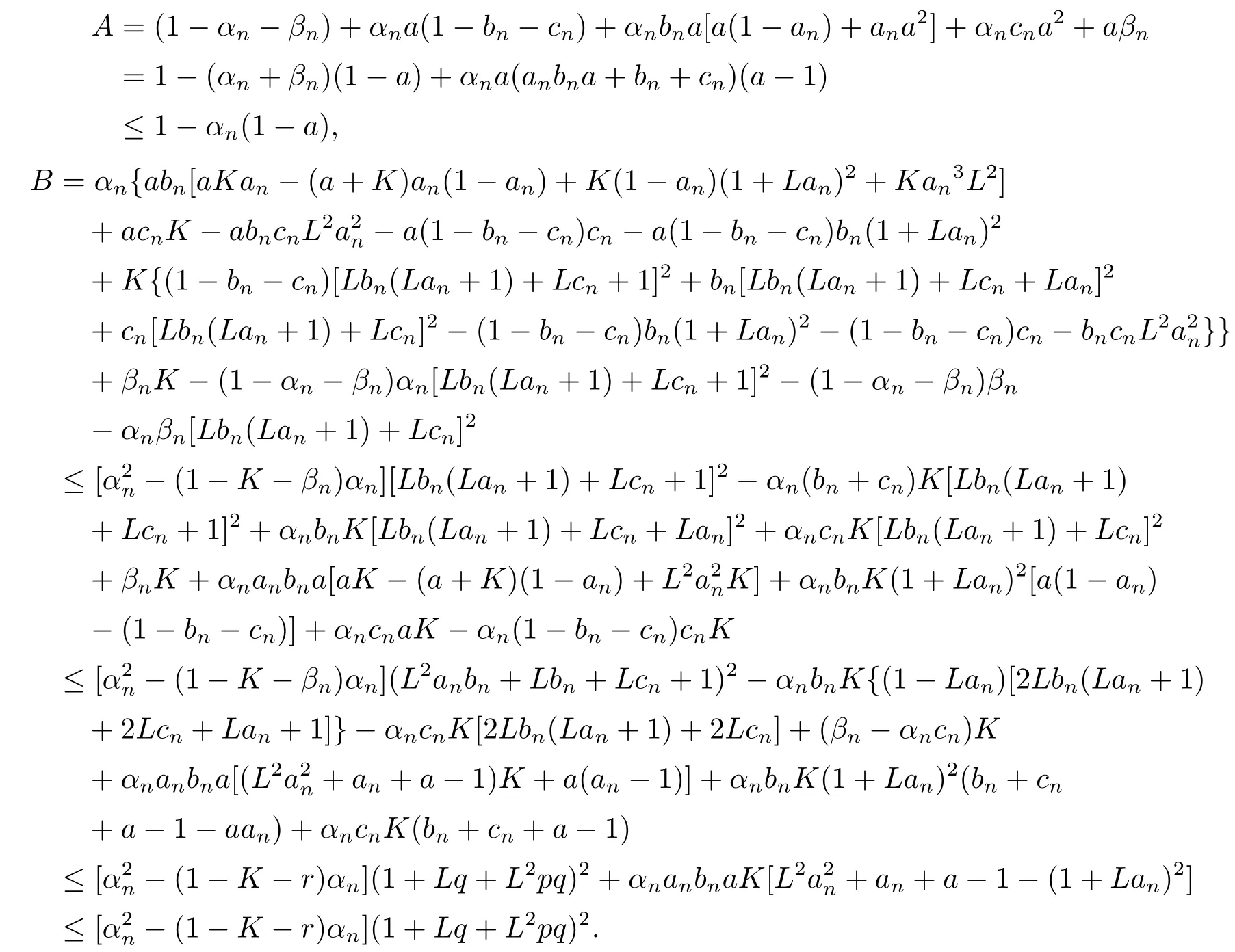
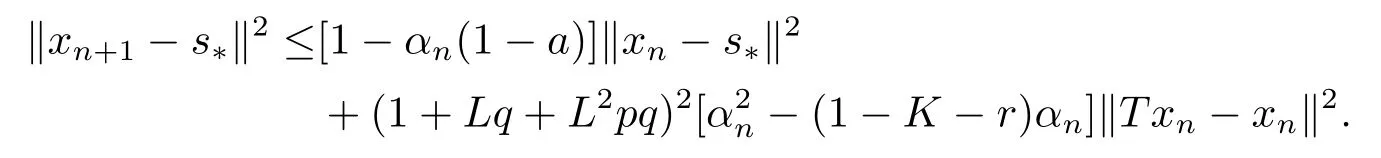
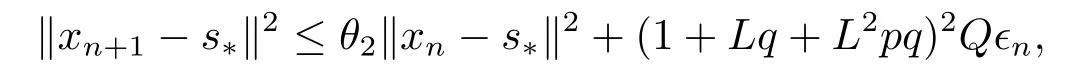

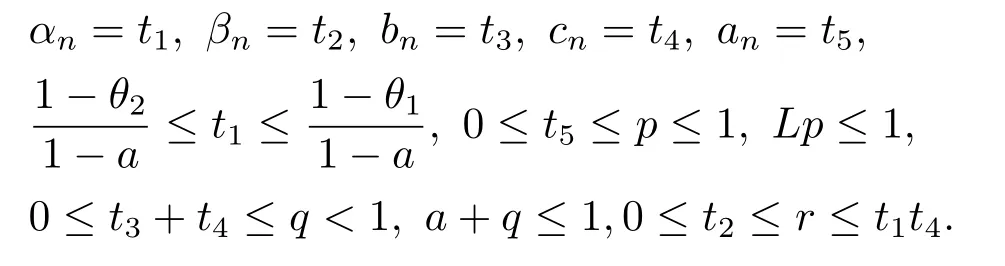
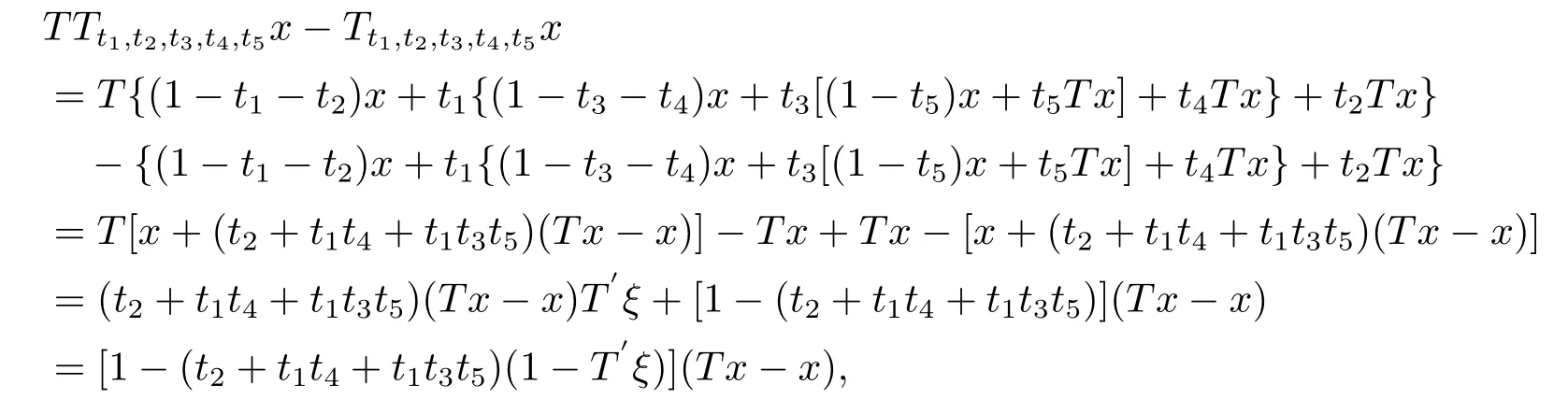
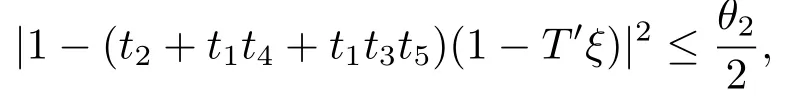
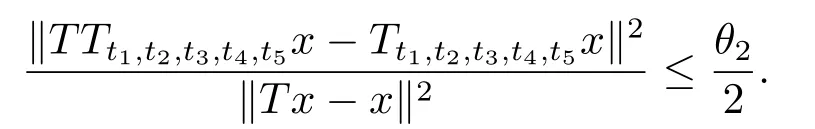
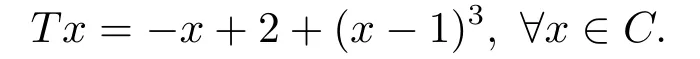


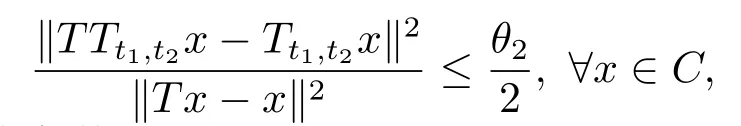



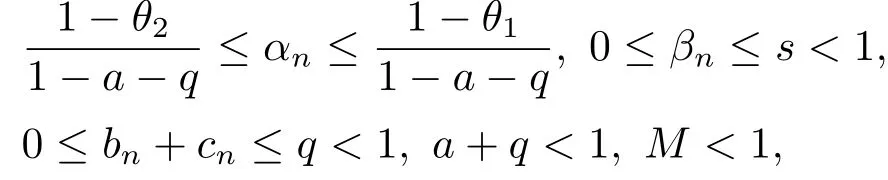

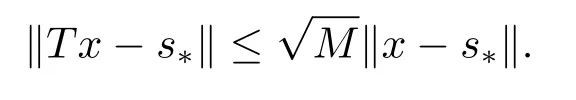
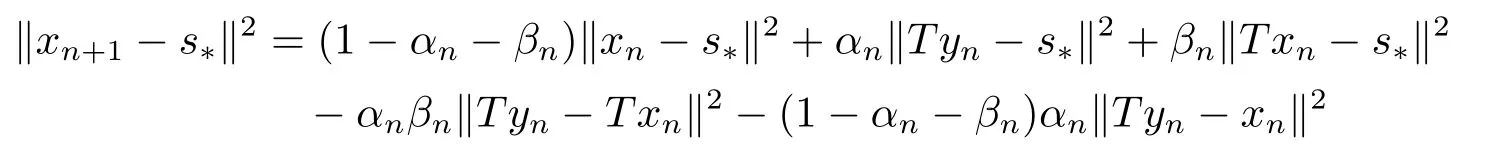
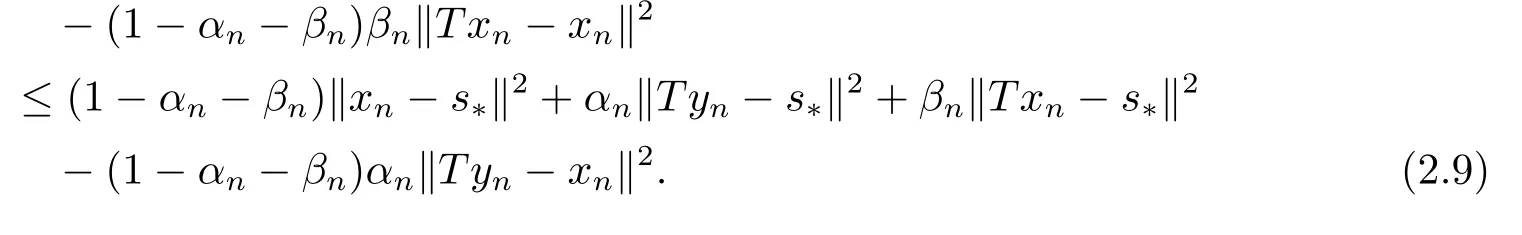

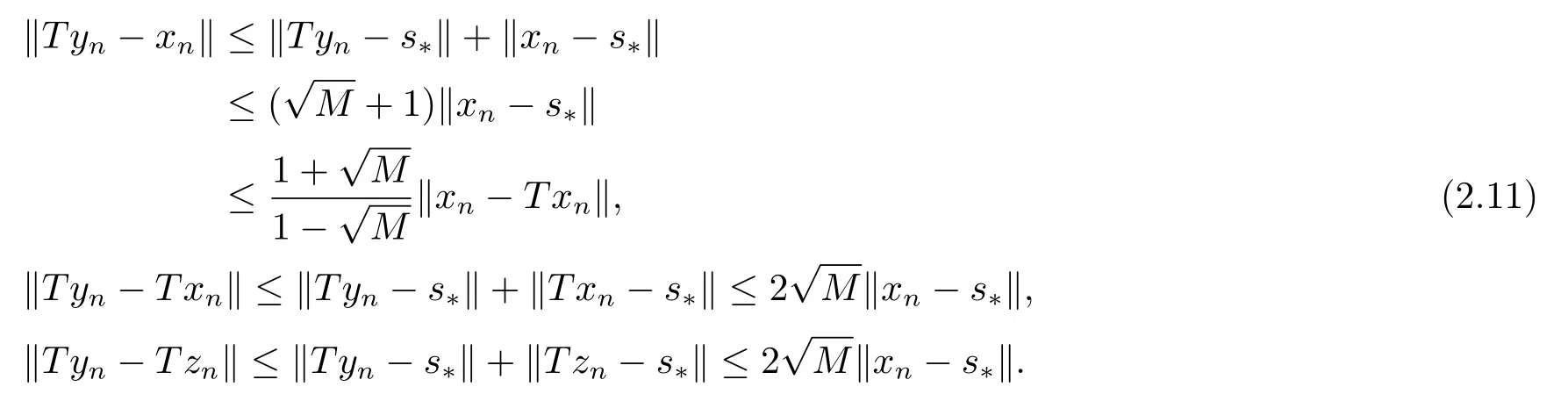
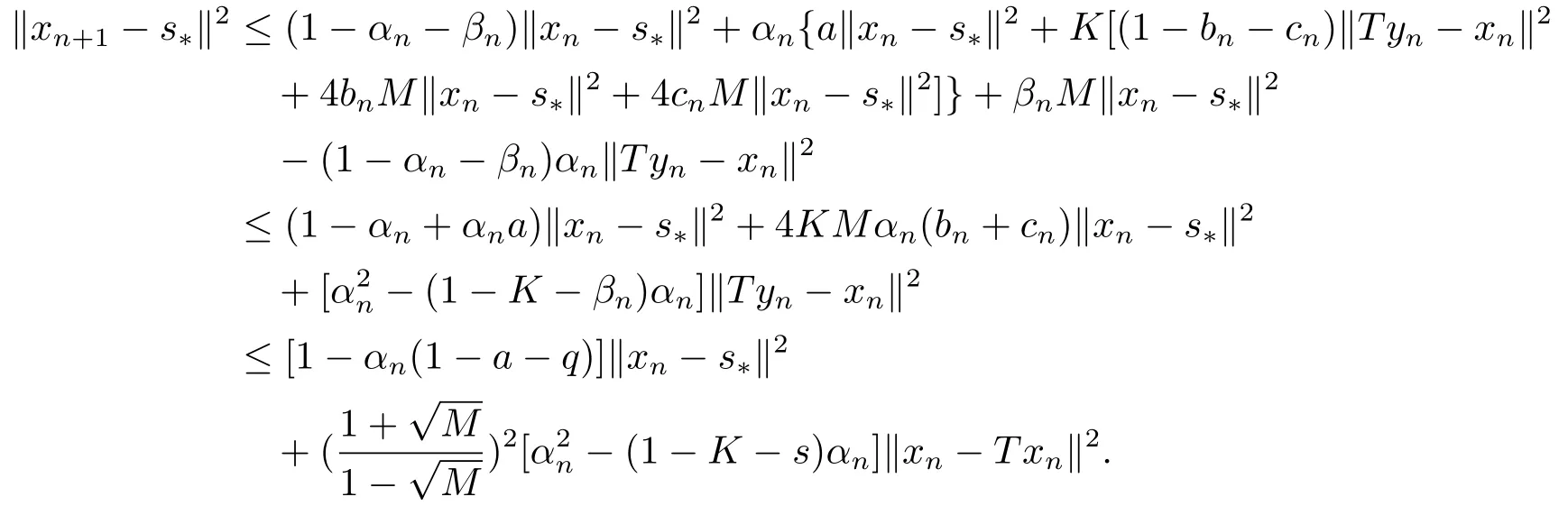
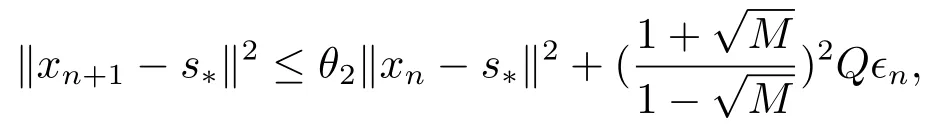
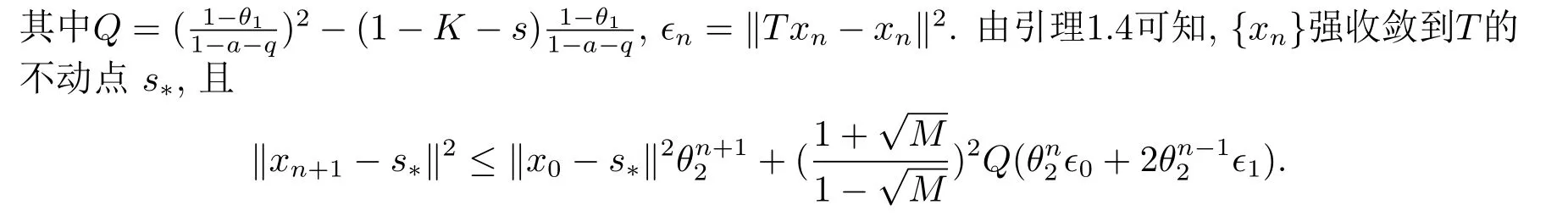
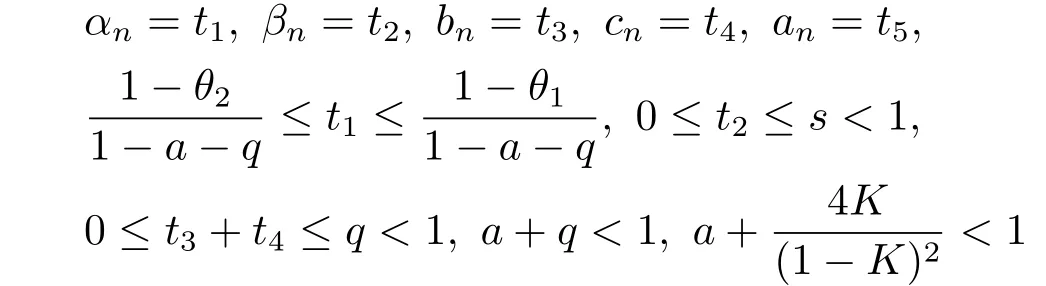

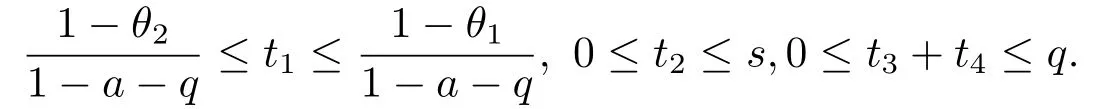
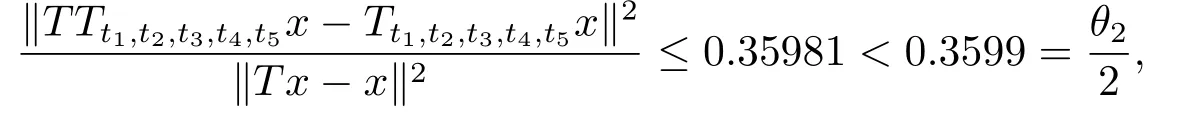
3.迭代序列(1.1)的T-稳定性