有关乘积群线性表示的若干结果及其应用
陈 智, 肖多晨
(合肥工业大学 数学学院,合肥 230601)
1 引 言
研究乘积群一直是研究群的重要手段之一,并且乘积群的线性表示已经成为进一步学习数学和其他诸多自然科学领域的知识的必备工具.这是因为一些乘积群的线性表示的结果已经不仅仅出现在数学领域,它还在其它理科中有着广泛的应用.目前,有限群表示的乘积理论已经被人所熟知了,如文献[2]与文献[3];但是无限群表示的张量积的相关结果的文章还很少.文中的证明加上一个自然的条件,就可以得到两个无限群作直积后的不可约表示是两个无限群的不可约表示的张量积.在此,感谢在论文写作过程中汪永杰教授提出的宝贵意见.
2 主要定理
本文仅考虑群的复线性表示.
定理1[1]设G是有限群,它包含有限群G1和G2作为子群,G=G1×G2,且ρ1∶G1→GL(V1)和ρ2∶G2→GL(V2)分别是G1和G2的线性表示,若ρ1和ρ2都是不可约的,则ρ1⊗ρ2是G1×G2的不可约表示.
下面对这一定理进行推广,当G=G1×G2,其中G,G1,G2均为可数无限群且V是可数无限维,再加上一个自然的条件,那么就能保证结论仍成立.

证先证充分性.若V≅V1⊗V2,其中V1,V2分别为G1和G2的不可约表示,为了后面叙述方便令此同构映射为τ.现在任取v2∈V2,则有V1⊗v2⊂V1⊗V2,即V1⊗v2是V1⊗V2的子表示.又因为τ∶V→V1⊗V2是同构映射,故τ-1(V1⊗v2)就是V的一个子表示.
任取g1∈G1,由于
g1·(τ-1(V1⊗v2))=τ-1((g1·V1)⊗v2)=τ-1(V1⊗v2),
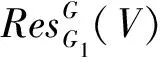


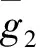

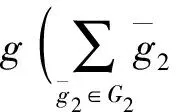
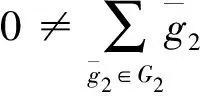

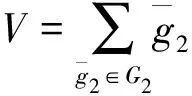

{uj⊗ws|j∈J,s=1,2,3,…};
作映射
φ∶V→W′⊗W,gj·wsuj⊗ws,
则φ是一个线性同构映射,于是可以利用映射φ从G=G1×G2在V上的作用得到一个G=G1×G2在W′⊗W上的作用.

将上述G1在W上的作用记为ρ1,即ρ1∶G1→End(W),此时上述作用可改写为



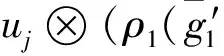

下面介绍舒尔引理:
引理2(舒尔引理) 若F为代数闭域,V是群G的不可约F表示,f∶V→V是同态映射,则存在常数λ∈F,使得f=λ·idv.


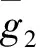
此时要分两种情况讨论:
① 若k∈J,则λh·gk·w∈V;
② 若k∉J,先定义:在I={i1,i2,i3,…,in,…}中,对于任意的is,it∈I,若is排在it的前面,则称is (*) ψiα∶W→W,wwiα, 故ψiα是G1同态映射.由舒尔引理可知wiα=λiα·w,λiα为常数.综上,可得到 因此可类似定义G2在W⊗W′上作用 将上述G2在W′上的作用记为ρ2,即ρ2∶G2→End(W′);此时G2在W⊗W′上作用可以写成 故 因此ρ2是G2的一个表示. 于是得到了G1×G2在W⊗W′上的表示,记为ρ1⊗ρ2. 下证映射 φ∶V→W⊗W′,gj·ww⊗uj, 又因为φ显然是既单又满,因此φ是G模同构映射,即V≅W⊗W′. 此时容易看出,以下引理成立: 引理3设G是无限群,它包含可数无限群G1和G2作为子群,G=G1×G2,(ρ,V)是G的可数无限维不可约表示,且V≅W⊗W′,其中(ρ1,W)是G1的表示,(ρ2,W′)是G2的表示.则ρ1、ρ2均为不可约表示. 根据上述引理可知,(ρ1,W)是G1的不可约表示,(ρ2,W′)是G2的不可约表示,又因为G=G1×G2,V≅W′⊗W可得:ρ=ρ1⊗ρ2,必要性得证.故定理得证. 根据上述定理,还可以得到一个推论: v1⊗V2⊂V1⊗V2, 即v1⊗V2是V1⊗V2的子表示.又τ∶V→V1⊗V2是同构映射,故τ-1(v1⊗V2)就是V的一个子表示.任取g2∈G2,由于 g2·(τ-1(v1⊗V2))=τ-1(v1⊗(g2·V2))=τ-1(v1⊗V2), 本文把有限群不可约表示张量积的定理通过加上一个自然条件推广到了任意可数无限群和无限维表示情形.本证明依赖于列举出一组表示的基,以及列举出陪集,所以不适用于不可数无限群和不可数无限维表示情形.这些更复杂的情形可作为进一步考虑的问题.此外,与有限群相比关于无限群的表示结论较少,还没有一套完整的理论.希望本文主要定理及推论有助于理解可数无限群表示这一前沿课题. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.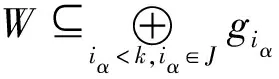
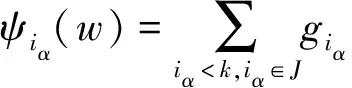

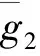
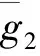
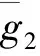

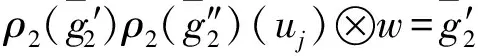
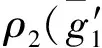

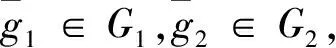
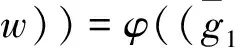



3 结 论

