Multi-temperature modeling of femtosecond laser pulse on metallic nanoparticles accounting for the temperature dependences of the parameters

Victor K.Pustovalov

ABSTRACT This review considers the fundamental dynamical processes of metal nanoparticles during and after the impact of a femtosecond laser pulse on a nanoparticle,including the absorption of photons.Understanding the sequence of events after photon absorption and their timescales is important for many applications of nanoparticles.Various processes are discussed,starting with optical absorption by electrons,proceeding through the relaxation of the electrons due to electron–electron scattering and electron–phonon coupling,and ending with the dissipation of the nanoparticle energy into the environment.The goal is to consider the timescales,values,and temperature dependences of the electron heat capacity and the electron–phonon coupling parameter that describe these processes and how these dependences affect the electron energy relaxation.Two-and four-temperature models for describing electron–phonon relaxation are discussed.Significan emphasis is paid to the proposed analytical approach to modeling processes during the action of a femtosecond laser pulse on a metal nanoparticle.These consider the temperature dependences of the electron heat capacity and the electron–phonon coupling factor of the metal.The entire process is divided into four stages:(1)the heating of the electron system by a pulse,(2)electron thermalization,(3)electron–phonon energy exchange and the equalization of the temperature of the electrons with the lattice,and(4)cooling of the nanoparticle.There is an appropriate analytical description of each stage.The four-temperature model can estimate the parameters of the laser and nanoparticles needed for applications of femtosecond laser pulses and nanoparticles.

KEYWORDS Femtosecond pulse,Nanoparticle,Metallic,Model,Thermal processes,Analytical solution

I.INTRODUCTION

The widespread use of femto-and picosecond lasers for metal processing,characterizing nanomaterials,laser nanomedicine,etc.depends on various processes that occur during laser–matter interactions.1–6The impact of femtosecond laser pulses,which have a characteristic duration of about 10–100 fs,on metals leads to the absorption of laser energy by free electrons.The electron gas oscillates due to an electric field and a nonthermal distribution of hot electrons is created.Electron–electron scattering and electron collisions with the metal surface result in the thermalization of the electron system at an elevated electron temperature,which can reach tens of thousands of kelvins.The electron temperature decreases after energy is exchanged between the electrons and phonons,and the system eventually relaxes back to the lattice temperature.The lattice temperature increases and can reach hundreds or thousands of kelvins after this exchange.Subsequently,the temperatures relax back to the ambient temperature due to thermal diffusion.

Theoretical and experimental studies of the interaction of picoand femtosecond laser pulses with metals began more than 30 years ago.7–14The heating of a metal sample by ultrashort laser pulses and its cooling after the termination of the laser beam are usually nonlinear.Characteristics of metals such as the electron–phonon coupling parameter and electron and lattice heat capacities depend on the electron temperature.Various results of recent studies and applications of the effect of ultrashort(femto-and picosecond)laser pulses on bulk metals and thin film can be found in the literature.4–6,15–18

The firs studies of pico-and femtosecond laser pulses incident on metallic nanoparticles(NPs)were presented in Refs.19–25.The particle temperature can reach or even exceed the melting or critical temperatures of the metal,which leads to thermal melting of the NP,its evaporation or fragmentation,and the formation of bubbles in a liquid medium,if the laser fluenc is sufficientl high.The latest results and applications of femtosecond-NP interaction processes have been presented in recent publications and reviews.26–30

The unique plasmonic properties of metallic NPs combined with recent advances in the development of ultrashort laser systems make such NPs particularly suitable for various applications of nanotechnology.A constantly growing number of modern laser/NP applications relies on the interaction of femtosecond laser pulses with metallic NPs.These include processing of the NPs,size reduction,melting and spheroidization,formation of NP ensembles,and the formation of nanobubbles around the NPs.Over the past decade,metallic NPs have found numerous applications in laser nanotechnology,1–6,31chemistry and medicine32–36(especially the application of NPs in laser nanomedicine for cancer treatment34–36),and other fields

Hot carriers generated by light can be used to drive a wide range of physical and chemical processes.The laser-induced production of hot electrons has attracted a great deal of research interest due to its potential for applications in photonics,electronics,photocatalysis,photoelectronics,and energy harvesting.37–39

The electron system of an NP can be excited by laser pulses.The resulting hot electrons determine the dynamics and subsequent processes during the irradiation.The time evolution of the electron energy distribution strongly depends on the total amount of energy absorbed,which,in turn,is determined by the particle size,pulse fluence photon energy,etc.The femtosecond interactions of a laser with a particle cause a significan increase in the temperature of both the particle and its surroundings,triggering several key processes.It is very important to account for the temperature dependences of the electron–phonon coupling parameter and the electron heat capacities of a metallic NP when irradiated by a femtosecond laser pulse,as these have significan effects on what occurs.

The temperature dependences of various processes involving hot electrons in bulk metals(films and metallic nanostructures(NPs)are general,and accordingly,the results for these metals objects will be discussed in this review.The review presents experimental and theoretical results describing the main features of the interaction of femtosecond laser pulses with the NP electron system and the NP lattice system.

II.TWO-TEMPERATURE MODEL OF ELECTRON–PHONON RELAXATION IN METAL

Research into the interaction of ultrashort laser pulses with metals began after the creation and development of picosecond and then femtosecond lasers.Compared with nanosecond pulses,it is more difficul to study the heating of the metal due to the absorption of laser energy by the electrons in the metal and the subsequent transfer of the energy absorbed by the electrons to the lattice.These processes were firs studied theoretically by Anisimov et al.,7based on the results in Ref.40.The phenomenological two-temperature model(TTM)was proposed7and adopted to study the energy relaxation under excited nonequilibrium conditions in metals.After that research,there were many further studies of the interaction of ultrashort laser pulses with electrons.

The TTM equations describe the electron–phonon coupling immediately after the establishment of thermal equilibrium separately in the electron and phonon subsystems and after the irradiation of the laser pulse on the metal:7

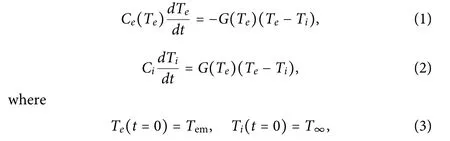
and where Ceand Ciare the heat capacities of the electron and lattice subsystems,respectively.Teand Tiare the temperatures of the electrons and lattice(ions),respectively.G is the electron–phonon coupling factor,Temis the maximum electron temperature at the end of the pulse,and T∞is the initial ambient temperature.Thermal equilibrium is assumed to be established in the electron and lattice subsystems,so that Teand Tiare well defined The heat capacity Ciof the lattice depends weakly on the temperature Ti,so it is usually assumed that Ciis a constant.41It is assumed that the electron conductivity and diffusion are negligible in femto-to picosecond time intervals.12The two-coupled kinetic Eqs.(1)and(2)describe the time evolution of the electron temperature Teand the lattice temperature Ti.The firs equation describes the thermal transfer of the energy of the electron gas to the lattice,and the second describes the heating of the lattice.In this model,the evolution of the energy flu and the electron–lattice relaxation kinetics are controlled by the electron–phonon coupling factor G.

On timescales of less than a hundred femtoseconds after the end of a femtosecond pulse,the electrons may not be in equilibrium,so that TTMfails to predict some of the main physical features of the ultrafast relaxation dynamics of metallic systems.Electrons,driven out of thermodynamic equilibrium by the ultrafast excitation,are thermalized on a characteristic timescaleτeeand establish a new equilibrium state due to electron–electron collisions.The simple and appealing TTMapproach has been applied to study the energy relaxation under the excited but equilibrium conditions in metal NPs,films or bulk metal and to study the ultrafast electron–lattice dynamics in a metal.7–12

To get a correct description of the various processes,it is very important to understand the temperature dependences of Ce(Te)and G(Te).Despite the widespread use of TTM,these key dependences remain the least known over wide temperature ranges.A key challenge in the quantitative application of TTMis the determination of these temperature-dependent parameters Ceand G.This review presents data from a first-principle theoretical approach and experimental results for the temperature-dependent Ce(Te)and G(Te).

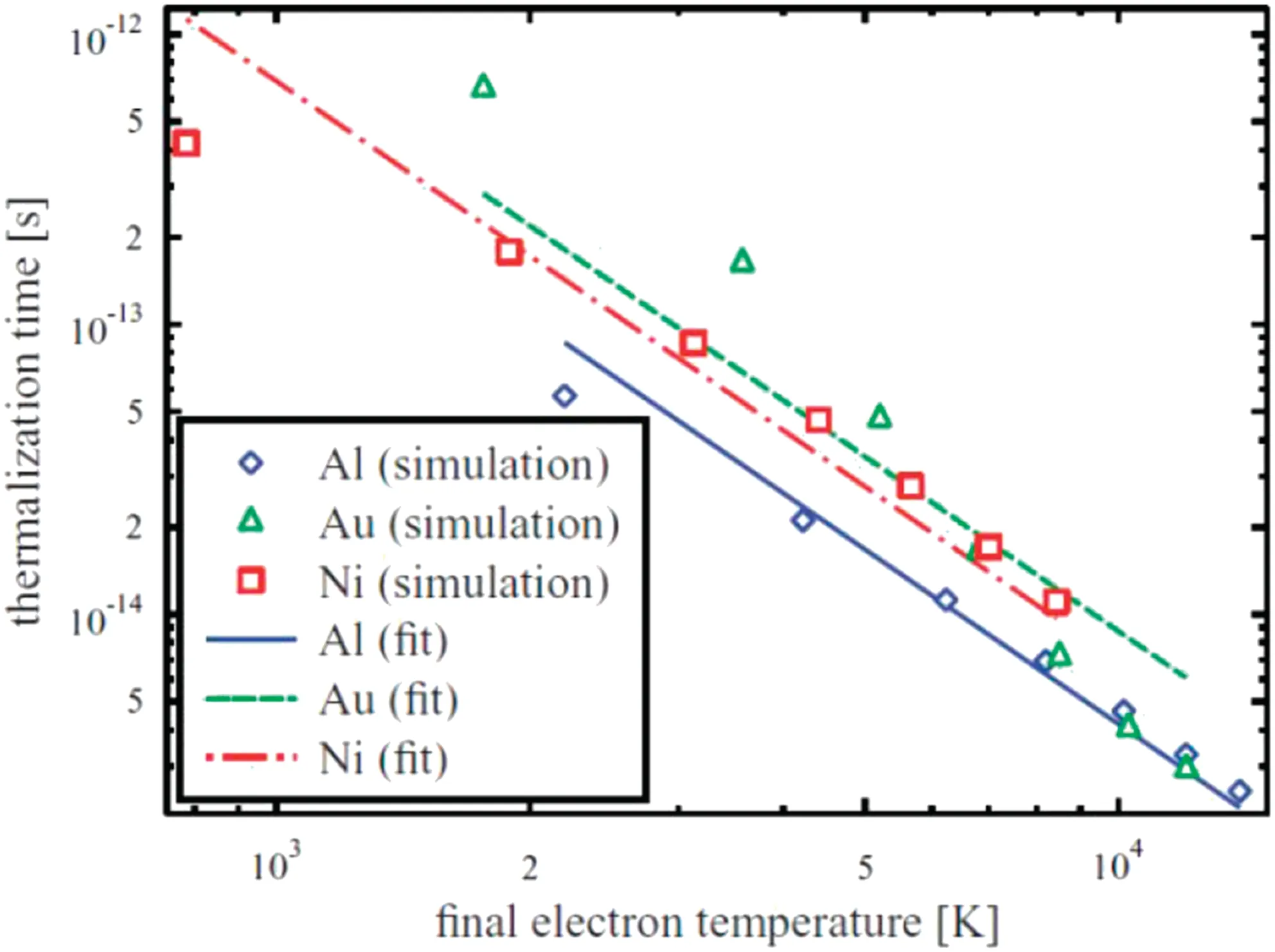
FIG.1.Thermalization timesτee plotted againstthe finalelectron temperatures after thermalization.Adapted from Ref.44 with permission from APS.

III.ELECTRON THERMALIZATION IN METALS

When an ultrashort laser pulse of duration tPirradiates a metal,the energy is absorbed by the electron system,which is driven out of thermal equilibrium on a femtosecond timescale.A state of thermodynamic equilibrium inside the electronic system is established within the time interval tP≤t≤τeedue to electron–electron collisions and electron collisions with the metal surface,whereτeeis the characteristic thermalization time.The energy absorbed by the electrons is transferred to the phononic system.The energy relaxation of electrons and their thermalization in metals have been studied by many researchers.Electron energy relaxation times τee＜1.5 ps were experimentally detected by time-resolved electrontemperature measurement in a highly excited gold target using femtosecond thermionic emission.10

Reference 11 assumed the existence of two thermalized electron subsystems with different temperatures.Thermalization in metals was studied using transient thermo-modulation transmissivity and reflectivit using a tunable multiple-wavelength femtosecond pump–probe in optically thin gold films11A phenomenological description of the electron gas was obtained by dividing the electron distribution into a high-density thermalized distribution and a very-low-density nonthermalized distribution with a characteristic electron-thermalization time of the order of 500 fs.These results are consistent with a model based on calculations of the electron-thermalization dynamics using numerical solutions of the Boltzmann equation.The evolution of an electron–phonon coupled system can be modeled by extending the TTM using three coupled differential equations with two electron temperatures.Nonstationary density functional theory has been used to analyze the nonequilibrium dynamics of laser-excited electrons in transition metals(Ni,Cr,and Cu).42Excited by a 7-fs laser pulse,d-block transition metals have two subsystems of electrons,each with its own temperature.Due to the higher localization,electrons from the d block remain cold,while excited delocalized sp electrons quickly reach a high temperature.The electrons of each energy band are mutually thermalized during the duration of the laser pulse.However,it takes much longer for the entire electronic system to reach equilibrium.

Electron–electron interactions have been investigated using a 25-fs Ti:sapphire oscillator and pump–probe measurements in optically thin silver and gold polycrystalline films43After internal thermalization,the electron distribution,its total energy,and dynamics can be completely characterized by the temperature Te.The internal thermalization of the nonequilibrium electron distribution created by the intraband absorption of the pump pulse occurs with a characteristic time of～350 fs.

The complete Boltzmann collision integrals have been used to describe the transient electron distribution due to excitation,thermalization,and relaxation.44Thermalization returns the electron system to a new equilibrium state with a distinct temperature.Thermalization has been analyzed for three metals after irradiation with the laser described above(wavelength of 800 nm and duration of 10 fs)and an absorbed fluenc of 0.12 mJ/cm2to verify the TTM assumptions.The electron-thermalization times for aluminum,gold,and nickel are plotted in Fig.1 as functions of the fina electron temperatures in the range Te=2×103–1.4×104K after thermalization.The curves agree well with an exponential fit The characteristic times are identifie with the thermalization timesτeefor aluminum,gold,and nickel asτee=11,47,and 86 fs,respectively.It was assumed that the density of states is such that it produces a free-electron-like system,so that screening is not explicitly accounted for and only electrons at the Fermi edge are considered.An approximate expression was proposed:τee=1/ATe2.For Au,the prefactor A=1.14×106K−2s−1.This temperature dependence saturates at high electron temperatures.Thus,the electron subsystem is thermalized in a characteristic time in the range of tens of femtoseconds for Te＞104K.

The ultrafast response of a bismuth surface was investigated using time-resolved photoemission spectroscopy.45It was found that electron thermalization depends on the fluenc and can take up to several hundreds of femtoseconds at low fluences Apparently,the observed changes of the optical properties are related to the nonequilibrium electron dynamics and not to the established effective electron temperature.The nonequilibrium electron dynamics,which have a sufficientl long electron-thermalization time,becomes important and limits the applicability of TTM.Experimental and theoretical results on the inelastic decay of optically excited electrons in different types of metals,including simple metals(Al),noble metals(Au,Ag,and Cu),transition metals(Ta,Mo,Rh,Co,Fe,and Ni),and rare earth metals(Gd,Tb,Yb,and La),have been reported.46The electron-thermalization time of about～20–200 fs in gold films depending on excitation energy,was determined by time-resolved two-photon photoemission.Using photoelectron spectroscopy with a time of 13 fs and sufficien angular resolution,various stages of the formation of a Fermi–Dirac distributed electron gas in graphite were traced after the absorption of an intense 7-fs laser pulse within the intervalτee≈50 fs after excitation.47The complicated relaxation of the excited electrons was theoretically studied with the Hubbard–Holstein model,which includes the three most important relaxation processes:(i)impurity scattering,(ii)Coulomb scattering,and(iii)electron–phonon scattering.48Experimentally,a nonequilibrium electron population is thermalized due to e–e scattering at Te≫Tbathin a few hundreds of femtoseconds.49A value τee≈600 fs has been determined,50which is consistent with the thermalization times previously measured in bulk gold.

In conclusion,note that the characteristic electronthermalization time in an optically excited metal depends on various experimental parameters,such as the type of metal,the form of the sample(bulk,film or NPs),impurities,laser wavelength,fluence and pulse duration,as well as on the theoretical approach and its limitations and accuracy.In any case,the data presented show that the characteristic range of electron-thermalization times in the approximate limit is of the order of aboutτee≈10–500 fs.Obviously,at a pulse duration of more than 100 fs,electron thermalization starts during the pulse irradiation.TTMis applicable after the completion of the electron-thermalization stage.

FIG.2.Comparison oftheoreticaland experimentalresults for the electron heat capacity Ce plotted against electron temperature T e for Au.The dotted line is for the linear factorγfrom the free-electron gas model,and the dashed line is for the linear factorγ=67.6 J m−3 K−2 from experiments.53 The theoreticalresults are from Refs.51,52,and 54.Adapted from Ref.52 with permission from Elsevier.

FIG.3.Evolution of the electronic heat capacity with T e for(a)Al,(b)Ni,(c)Cu,and(d)Au using differentLDA and GGA exchange and correlation functionals.GGAsc and LDAsc indicate that the effectof semicore electrons is accounted for.The dotted black curves are data from Ref.51.Adapted from Ref.56 with permission from Elsevier.

IV.DEPENDENCE OF ELECTRON HEAT CAPACITY ON TEMPERATURE

The temperature-dependent electronic heat capacity Ce(Te)is the most significan parameter,as it determines all subsequent processes due to the irradiation of metals(NPs)by femtosecond laser pulses.One of the firs theoretical investigations of the dependence of the electron heat capacity on the electron temperature was carried out for eight metals:Al,Cu,Ag,Au,Ni,Pt,W,and Ti.51A computational analysis based on first-principle calculations of the electronic structure of the electron density predicted large deviations of up to an order of magnitude from the commonly used approximations of the linear temperature dependence of the electron heat capacity Figs.2 and 3.

The calculated electron heat capacity plotted against the electron temperature is shown in Figs.2 and 3.Figure 2 shows values for gold in the temperature range up to 2×104K from various sources.The main influenc on the evolution of the electron heat capacity is mainly the density of electronic states and the Fermi–Dirac distribution.52The linear relation Ce(Te)=γTe,whereγis some parameter,is observed for Tebelow 3×103K for Au,as shown in Fig.2.The results show excellent agreement with the linear approximation withγfrom the free-electron gas model51and with experiment values withγ=67.6 J m−3K−2.53However,at high Te,there are significan deviations between the linear approximation and the calculated result,so that Ce(Te)for Au almost coincides with that given in Ref.54.

The electronic behavior of various metals(Al,Ni,Cu,Au,Ti,and W)under ultrashort laser irradiation has been theoretically studied using density functional theory.55The optical coupling and transport characteristics are usually modelled with the classical theory of free electrons.The number of free electrons depends on the electron temperature and has been evaluated for a number of metals for electron temperatures up to 105K within a cold lattice.The number of free electrons and the electronic heat capacities depend on the relation between the electron temperature and the density of nonequilibrium states.The local density approximation(LDA)and the generalized gradient approximation(GGA)have been used to calculate the electronic heat capacity as a function of electron temperature Ce(Te)for transition and noble metals.55,56Figure 3 shows the curves for gold,aluminum,nickel,and copper in the temperature range up to 105K from various sources.The validity of the free-electron approach,which varies the number of free electrons per atom,has been tested.This approach is suitable for simple metals only.For transition metals,the presence of localized d electrons leads to a strong deviation of the heat capacities at high energies,which means that more energy is required for thermal excitation than for free sp electrons.This is due to the effects of collective excitation,which are strengthened by the change in electronic screening at high temperature.

Measurements of transient absorption in thin gold film have been interpreted in accordance with several theoretical approaches with varying degrees of complexity,starting from a simple semiclassical TTM.57The expression Ce(Te)=γTe,withγ=65 J m3K−2for Ag and Au,is valid for noble metals as long as only quasi-free electrons in the conduction band participate in electron heating,i.e.,the excitation satisfieΔTe＜3000 K.At higher temperatures,thermal excitation of d-band electrons can lead to a modifica tion of the density of electronic states involved in electron–lattice interactions.

Approximating Cebased on temperature Tehas been widely used in theory and experiments in a limited interval of electron temperature Te＜(1–3)×103K for gold and other noble metals:

The calculations mentioned above give a nonlinear relation between Ceand the electron temperature Te,which tends to lead to saturation in the limit at high Te.One approximation is to use a power law:

whereα≈0.5–0.75 is some exponent.This is adequately fitte to Ce(Te)in Figs.2 and 3.Note that the lattice capacity has only a slight dependence on Teso a constant value of Cican be used.41

V.TEMPERATURE DEPENDENCES OF THE ELECTRON–PHONON COUPLING IN METALS

The energy exchanged between electrons and phonons in metals is important for describing the relevant processes,for understanding experimental results,for laser micro-and nanomanufacturing,and for applications in nanotechnology.Electron–phonon coupling is one of the most important phenomena governing the intensity of energy exchange after ultrafast energy deposition at the nanoscale,since nonequilibrium effects are significant In the standard approach,the energy transferred between electrons and ions can be modeled by the electron–phonon coupling parameter and the temperature difference.

In experiments,a laser pulse with a duration of 50–300 fs created a nonequilibrium electron distribution,leaving the lattice temperature Ti=300 K practically unchanged.Then,within a few hundred femtoseconds,the electrons returned to a local equilibrium at some elevated temperature,after which electron–phonon interactions caused energy to be exchanged between the electronic and lattice subsystems.Finally,a slower relaxation process dominated by heat diffusion returned the entire system to the ambient temperature.Accurate electron–phonon coupling factors for a wide variety of elements and over a wide temperature range are in high demand.

The microscopic foundation of TTM is based on the standard Bloch–Boltzmann–Peierls formulas.8The TTM equations provide a microscopic,theoretical description of the energy transferred in a system of electrons and phonons.A simple expression for the electron–phonon coupling parameter(or energy exchange rate)describes this process with adequate accuracy.

The development of ultrafast laser pulses has opened up a new fiel of time-resolved spectroscopy for experimental investigations of the thermal relaxation of hot electrons in metallic films One of the firs femtosecond pump–probe measurements of the electron–phonon coupling constant in thin metallic film of Cu,Au,Cr,Ti,W,Nb,V,and Pb is described in Ref.9.This method has a number of advantages over other methods,as it is a direct measurement of the interaction parameters at room temperature and is not affected by extraneous effects.The results of the TTM with constant G have been compared with experimental data.The agreement between the measured coupling constants and those obtained by other methods was good,which confirm the theoretical predictions.8

Direct measurements of hot-electron temperatures and relaxation dynamics found peak electron temperatures of between 3400 and 11 000 K for intensities～1.5×1011W/cm2using two-pulsecorrelation femtosecond thermionic emission.10The experiments were performed with laser pulses with a duration of 120 fs and a wavelength of 630 nm.Thin gold film prepared by evaporation onto a clean Si wafer were irradiated.The peak electron temperatures were measured for various time delays at the overall intensities and the results were compared with theoretical results.TTM was used with constant low-temperature values for Ceand G,but it was clear that these are poor approximations for Au in this high-temperature regime.

The dynamics of electrons and a lattice after the optical excitation of metals was experimentally studied using measurements of the linear and second-harmonic reflectivit with time resolution.12The pump–probe technique was used to study the relaxation of hot electrons by measuring the reflectivit when the electrons and lattice were in thermal equilibrium.For noble metals,the reflec tivity of the probe is related to the electron temperature using an appropriate model for the dielectric function.Electron–phonon coupling constants were presented for gold film with a thickness of 10–100 nm.These were obtained by fittin TTMresults to the transition coefficient for reflectio and transmission.Acomparison of the experimental and theoretical results showed that TTMis well suited for describing the thermal dynamics of hot electrons in metals and extracting electron–phonon coupling constants from experimental data.

Electron–electron and electron–lattice interactions were studied using a 25-fs Ti:sapphire oscillator and pump–probe measurements of optically thin silver and gold nanometer polycrystalline films43After internal thermalization,the distribution of electrons was completely characterized by their temperature Te.Further,the dynamics could be described by calculating the energy change in the lattice using the well-known system of TTM rate equations.These results were in quantitative agreement with numerical simulations of the electron relaxation dynamics using a reduced static screening of the electron–electron Coulomb interactions and including the screening of bound electrons.Experimental investigations8–12,43for the firs time provided data for the experimental determination of the coupling parameter for metal film(bulk metal).

One of the firs experimental studies of the energy exchanged between the electrons and the lattice in NPs was the investigation of the femtosecond response of electron–lattice interactions in single-metal NPs.58,59The energy exchanged was also studied in an ensemble of silver NPs with an average diameter of～9 nm and in a single 30-nm particle using a femtosecond pump–probe.58An analytical solution of the TTM equations with a constant value of G was compared with the experimental results.The measured transient changes in the transmission and kinetics of the electron energy loss,which depends on the excitation amplitude,were compared with the results of numerical simulations of nonequilibrium electron relaxation.Experiments59were performed on 20-and 30-nm silver nanospheres.The ultrafast nonlinear optical response of a single-metal NP was investigated by combining a highly sensitive femtosecond pump–probe with a spatially modulative microscope.The electron–phonon energy-transfer timeτeph≈850 fs was measured in an ensemble of silver NPs with an average diameter of 25 nm.Its experimental dependence on the electron temperature was quantitatively interpreted using TTM.These firs femtosecond studies of the transient absorption of a single-metal NP have opened up possibilities for a precise analysis of the ultrafast properties,electron kinetics,and electron–phonon energy-transfer time of a single-metal NP.

Investigations of electron–lattice energy transfer in small copper nanospheres,3.2–23 nm in diameter and embedded in glass or dispersed in a solvent,were presented using time-resolved ultrafast pump–probe spectroscopy.60TTM results with constant G were compared with experimental values.The rate of electron scattering in the lattice increased with decreasing size of the nanospheres.In the weak perturbation regime,the electron–phonon energy-transfer timeτeph=(0.97±0.10)ps was somewhat shorter than in bulk gold(～1.15 ps)and agreed with the values expected for gold NPs 17 nm in size.This confirm that the thermalization of the electron–lattice system in gold NPs accelerates with decreasing size of the NPs due to the decrease in the efficienc of screening near the NP surface.A theoretical analysis of the TTM predictions and a complete simulation of the extinction transition of the NP cross section by solving the Boltzmann equation in the presence of hot electrons were performed.

Note that estimating the temperatures Teand Ti,which are the main parameters in theoretical models,from experimental data is always indirect as a rule.An attempt has been made to solve this problem.61The dynamic optical response of plasmonic Au NP ensembles after excitation with an ultrashort pulse was measured and compared with the corresponding static optical response as a function of the increasing temperature of the thermodynamic bath.The ultrafast optical response following pulsed-laser irradiation was recorded with pump–probe transient absorbance spectroscopy.The static optical response was measured as a function of the thermodynamic bath temperature Tbathin the range 298–673 K.An evaluation of these two datasets made it possible to extract the experimental ultrafast temperature evolution of the plasmonic particles as a function of time.The energy exchanged between the population of excited electrons and the NP lattice via electron–phonon coupling led to thermalization on the timescale τeph≈10–30 ps.

FIG.4.Experimentalphotoemission spectra in the Fermi-edge region.Stationary data are from bulk Au(red symbols)and Au NPs(green symbols).The pump–probe spectrum of Au NPs atnegative delay(τ=−10 ps)is shown with blue symbols.The solid lines are the respective fitting curves.Adapted from Ref.65 with permission from Wiley.

The ultrafast relaxation and the subsequent release of energy to a low-energy distribution of thermalized hot electrons were studied with femtosecond transient-absorption spectroscopy(FTAS).62FTAS measurements with a pump–probe scheme were made using laser pulses with wavelengths of 405 and 810 nm,which irradiated a sample with an energy density of 20μJ cm−2.The sample consisted of a 2D array of Au NPs deposited onto a crystal surface.A combined approach was introduced that was based on post-processing of FTAS measurements guided by a version of TTM extended to the pump–probe experimental map recorded for a 2D array of isolated gold nanoellipsoids.An extended version of 2TM11was also used to provide a more accurate description of the dynamics of fast relaxation of a photoexcited nanostructure with constant G.

The femtosecond evolution of the electron temperature of laser-excited gold NPs was measured using ultrafast time-resolved photoemission spectroscopy induced by extreme-ultraviolet radiation pulses.63The temperature of the electron gas was determined by recording and fittin high-resolution photoemission spectra around the Fermi edge of gold NPs,which provided a direct picture of the ultrafast electron–gas dynamics.

Figure 4 shows three photoemission spectra measured in the Au Fermi-edge region as functions of the binding energy EF−E,where EFis the Fermi energy and E is the electron energy.The red symbols are reference measurements for a thick Au foil recorded using extreme ultraviolet only.The green symbols indicate the stationary spectrum of Au-NPs/AZO/MgO with a bare substrate,which consisted of a 150-nm-thick Al-doped ZnO(AZO)fil deposited onto a MgO substrate.The blue symbols are the spectrum of the Au NPs deposited onto the substrate.The blue open symbols are the pump–probe spectrum.There was a fast rise of Tewithin the firs few hundred femtoseconds,followed by a slow decrease over the following picoseconds,which is consistent with the general picture of the ultrafast electrodynamics in metallic NPs.The 3TMwas used to describe the experimental results.

The application of anti-Stokes photoluminescence of metal NPs has been extended to pulsed illumination and pump–probe anti-Stokes spectroscopy,which can measure the effective electron temperature in a gold NP(～103K under our conditions),as well as the ultrafast dynamics of an excited electron population with subpicosecond time resolution.50A train of pump pulses with a center wavelength of 785 nm and width of about 350 fs with a pulse energy of～2 pJ were used to irradiate a sample consisting of 100-nm gold nanospheres spin-coated onto a glass coverslip.Heating of up to Te=2×103K and the subsequent cooling of the electrons were measured with picosecond resolution.The TTMmodel was used to describe the experimental results.

The results of pump–probe measurements of plasmonic NPs have been presented along with a theoretical description based on first-principle calculations of the carrier dynamics and optical response.64The time-resolved differential extinction spectra were collected using a commercial Helios absorption spectrometer.The pump pulses were centered at 800 nm with a 1-kHz repetition rate.The duration of an amplifie pulse was～50 fs,and the fluenc was up to 110μJ/cm2.The sample was a solution of Au colloids with a diameter of 60 nm in water.The concentration was 2.6×1010particles cm−3.The evolution of the carrier distributions in time was described using the nonlinear Boltzmann equation.The temporal evolution of the measured and predicted differential extinction spectra of Au colloids for a probe wavelength of 530 nm are shown in Fig.5.64

Increasing the pump power generates more initial carriers.These equilibrate faster to a higher electron temperature,which subsequently relaxes more slowly due to the increase of the electron heat capacity.The theoretical results in an evaluation of the effects of the electronic structure on the density of states,the distribution of excited carriers,and electron–phonon coupling were in quantitative agreement with the spectral and temporal features found in transient-absorption measurements,without any of the fittin parameters that were typical in previous analyses.

FIG.5.Comparison ofmeasured and predicted differentialextinction spectra of Au colloids with a probe wavelength of530 nm and pump excitation at560 nm with intensities of 21,34,68,and 110μJ/cm2 as a function of time.(a)Comparison of absolute measurements(circles)and calculated values(solid lines)of the differentialcross section.Measurements(b)and predictions(c)normalized by the peak value over fulltime.Adapted from Ref.64 with permission from Wiley.

The temperature and lifetime of hot electrons in gold and copper nanostructures have been measured under stationary illumination by a continuous-wave Nd:YAG laser with a wavelength of 532 nm and by continuous-wave anti-Stokes Raman spectroscopy.65The nanostructure consisted of nanopillars with a diameter of 250 nm and a height of 100 nm.Using a modifie version of TTM,we calculated the coupling constant G≈1015to 1016W/m3K.This constant characterizes the rate of energy transfer from the hot electron population in these metals.This result is consistent with previous results.Very long lifetimes of up to 10 ns were recorded for the hot electrons in both metals with a stationary Raman signal,unlike the picosecond lifetimes commonly measured in ultrafast transient-absorption experiments.57–64However,it has been hypothesized that the long lifetimes may indicate that multiple photon absorption events excite the hot electrons,effectively extending their lifetime,before they are thermalized along with the lattice.

The ultrafast laser excitation of metals leads to nonequilibrium states in which the solid–liquid phase transition has complex dynamics.Electron diffraction at mega-electron-volt energies has been used to visualize the ultrafast melting of 35-nm-thick singlecrystal and 30-nm-thick polycrystalline gold foils,which were excited by 130-fs 400-nm laser pulses.66Three melting regimes were identifie from the measurements:homogeneous,heterogeneous,and incomplete melting.There was evidence for the heterogeneous coexistence of solid and liquid phases,the evolution of the ion and electron temperatures,and an overheated state.The entire data set for the three melting regimes was based on only a single assumption that the electron–ion coupling parameter G weakly depends on the energy density.It increased modestly from 2.2×1016Wm−3K−1at the lowest energy density to 4.9×1016Wm−3K−1for the maximum energy density.Data from single-crystal samples was in functional agreement with a combined TTM and molecular dynamics simulation results for single-crystal gold.These results for G(Te)are shown in Fig.6.

TTMhas been used to describe electron–phonon processes in film9–12and in NPs.43,50,58–60,62–64The measured changes in the transient transmission and the kinetics of electron energy losses have been compared with the results from numerical simulations of nonequilibrium electron relaxation.The comparison showed that TTM is well suited for describing the diffusion of hot electrons in metals and extracting electron–phonon coupling constants from experimental data.The experimental evolution of the electron temperature over time has usually been interpreted quantitatively using TTM.The electron and phonon parameters have been determined using a constant value of the electron–phonon coupling parameter G and the linear dependence of the electron heat capacity on temperature Ce=γTe.

An extended 3TM has been proposed11and used to describe the results of experiments.62,633TMis a thermodynamic model that describes the dynamics of an energy flo after the photoexcitation of noble-metal structures in terms of the three energetic degrees of freedom:the excess energy density of the nonthermal electrons,the temperature of thermal electrons,and the lattice temperature.This model probably provides a more accurate description of the fast relaxation dynamics of a photoexcited nanostructure,since it not only accounts for the temperatures of the electron bath and the lattice but also the initial nonthermal distribution of electrons with constant G.62,63,65However,the main problems with 3TM are that it is unable to describe nonthermal electrons without the correct temperature and that it cannot determine the initial numbers of nonthermal and thermal electrons immediately after the end of the pulse.The results of a combined TTM and molecular dynamics simulation showed functional agreement with the data for crystalline gold samples.63

Many theoretical investigations of the electron–phonon coupling parameter G have been based on calculations from so-called firs principles.Theoretical studies of the dependence of the strength of the electron–phonon coupling on the electron temperature have been carried out for eight representative metals(Al,Cu,Ag,Au,Ni,Pt,W,and Ti)where there is a strong electron–phonon nonequilibrium of metal targets subjected to short pulses of laser irradiation.51Acomputational analysis based on first-principle calculations of the electronic structure of the electron density of states predicted large deviations,up to an order of magnitude,from the commonly used electron–phonon coupling constant.With increasing electron temperature,the strength of the electron–phonon coupling can increase for Al,Au,Ag,Cu,and W,decrease for Ni,Pt,and change nonmonotonically for Ti.The large variations in the thermophysical properties,as found in research on electron temperatures up to 2×104K,are typically realized in applications of femtosecond laser processing of metals and are of great importance for the quantitative analysis of the ultrafast processes associated with the laser irradiation of metals.

FIG.6.(a)Electron–phonon coupling parameter G(T e)(1017 W m−3 K−1)in gold calculated with XTANT-3 compared with various theoreticaland experimentaldata.The experimentaldata are from Refs.9,12,66,and 76–81.Theoreticalresults are from Ref.51(and the same data rescaled by a factor of 1/4)and Refs.10,68,69,82,and 83.There are two curves from Ref.67.(b)Plotof G(T e)(1017 W m−3 K−1)in platinum calculated with XTANT-3 compared with various theoreticaland experimentaldata.The experimentaldata are from Refs.12 and 84–86..The theoreticalestimates are from Ref.51(and the same data rescaled by 1/4)and Ref.83.Adapted from Ref.82 with permission from APS.

Using a kinetic equation,the thermal conductivity and the electron–ion heat transfer coefficient in condensed media have been calculated in the temperature range 1–50 K for noble and transition metals using a strongly excited electron subsystem,a matrix element for the scattering probability,and a screened Coulomb potential that describes the interactions between charged particles.67Electron–phonon relaxation and the melting of thin film of copper,gold,and platinum during nonequilibrium heating by femtosecond laser pulses have been theoretically investigated with first-principle calculations.68There have been ab initio first principles calculations and experimental investigations of phonon coupling,the optical response of hot electrons in plasmonic metals,and the ultrafast carrier dynamics in plasmonic NPs.69The electronic heat capacity and the electron–phonon coupling strength have been simulated for electron temperatures of up to 8×103K for Al,Ag,Au,and Cu.Substantial differences from free-electron and semiempirical estimations were found,especially in noble metals above the transient electron temperature of 2000 K.

Some investigations of nonequilibrium effects in electron–phonon interactions use the Boltzmann transport equations with collision integrals.37,44,70,71The full Boltzmann equations and implementations of the density of states of real materials have been applied to describe transient electron distributions due to excitation,thermalization,and relaxation without the need to assume thermalized electrons.44A theoretical study of the temporal evolution of optically excited conduction electrons in small plasmon-supporting gold and silver NPs was carried out.The electron distribution was obtained,and its thermalization takes 10 fs.37The dynamics of electrons has been described in terms of a master equation involving transition rates for optical excitations and electron–electron collisions.It strongly depended on the total absorbed energy,which in turn was determined by particle size,pulse fluence and photon energy.Electron and phonon thermalization in simple metals excited by a laser pulse has been numerically studied by solving the Boltzmann equation and accounting for electron–electron,electron–phonon,phonon–electron,and phonon–phonon scattering.70Electron–phonon coupling has been identifie under nonequilibrium conditions for aluminum,gold,and nickel.An electron–phonon coupling model was proposed by transforming the full scattering terms into approximate forms of the relaxation time in the coupled electron and phonon Boltzmann transport equations.The model was verifie by femtosecond pump–probe experiments on a metal surface.71The coupling constant was very much lower both,because of the temporal nonequilibrium between the different phonon branches and because of the spatial nonequilibrium of the electrons.

There has been a direct comparison of the theoretical results obtained from firs principles and from TTM.44,70,72,73For low excitations,TTM does not apply immediately after the laser irradiation due to the slow thermalization.However,it is applicable for high irradiation intensities and free-electron-like metals.44Electron–phonon coupling and the corresponding energy exchange have been investigated by ab initio theory for nonequilibrium states of aluminum.73The electron–phonon coupling strength has been derived for a range of electronic and lattice temperatures from density functional theory through molecular dynamics simulations.The results are in excellent agreement with time-resolved experimental diffraction data.The electron–phonon coupling parameter,extracted from experimental data using TTM,was～2 times smaller than the values from an ab initio nonthermal lattice model that describes nonthermal phonon distributions.This discrepancy is small enough that the approach can be used with sufficien accuracy.The relaxation dynamics in simple metals excited by a laser pulse has been studied with TTM.Note that TTM underestimated the electron–phonon coupling constant in metals,70which is consistent with previous results.73A theoretical study was done of the nonequilibrium electron and phonon dynamics in metals after femtosecond laser excitation.72A parameter-free microscopic nonequilibrium model has been applied to describe the ultrafast laser-induced phonon and electron temperature dynamics of various metallic systems,such as gold,aluminum,iron,nickel,and cobalt.Deviations from TTMon a picosecond timescale were recorded for all the materials studied,even for gold.The rate of energy transfer between electrons and phonons has been investigated in aluminum and copper from firs principles for electron temperatures up to Te=5×104K.The lattice was considered to be in the ground state.74These data for the coupling electron–phonon parameter G(Te)51,67–69are plotted in Fig.6.

The dynamical coupling approach for calculating the energy exchanged between electrons and ions in nonequilibrium metals has been implemented in the tight-binding molecular dynamics code XTANT-3,which has been used to study electron–phonon coupling in various elemental metals.75The XTANT-3 code is a universal scheme applicable to electron temperatures up to 2×104K and to arbitrary atomic configuration and dynamics.The calculated electron–ion and electron–phonon coupling parameters are in good agreement with the available experimental data in the regime of a determined electron temperature,which confirm the correctness of the model.The following materials are studied here:face-centered cubic metals(Al,Ca,Ni,Cu,Sr,Y,Zr,Rh,Pd,Ag,Ir,Pt,Au,and Pb),hexagonal close-packed metals(Mg,Sc,Ti,Co,Zn,Tc,Ru,Cd,Hf,Re,and Os),and body-centered cubic metals(V,Cr,Fe,Nb,Mo,Ba,Ta,and W).An estimate of the electron–phonon coupling at elevated electron temperatures is given,which can be used in various models simulating the ultrafast deposition of energy into matter.

The results of the XTANT-3 simulation for gold(Fig.6)are consistent with the experimental points at high electron temperatures,66whereas the values from other approaches typically tend to be overestimates.However,the results in Ref.51 rescaled by 1/4 agree with the experimental data.The data in Refs.68 and 69 were calculated for a slower increase in coupling,and only the results in Ref.82 are in good agreement with XTANT-3 and experimental points.The coupling parameter increased by up to two times over the entire temperature range,as determined by the value reached at the maximum electron temperature.66These experimental data are best reproduced by TTM,which agrees with the calculations.75There was a slow increase of the coupling parameter with an increase of the electron temperature,along with a similar weak dependence for gold.54On the other hand,the theoretical coupling parameters51,67,68significantl increased by up to 5–10 times with an increase of the electron temperature.

The electron–phonon coupling parameter for platinum is shown in Fig.6(b).The calculated values51for platinum were adjusted to experimental data points at room temperature.86The data from Refs.12 and 84 are close to the XTANT-3 predictions.There was a characteristic decrease in the coupling strength due to an increase in Teover the entire temperature range up to 2×104K.51,67,68

Such discrepancies in the temperature dependences are open questions due to a lack of experimental data for the electron–phonon coupling strength in the high-electron-temperature regime for various materials,as this is the most important value in the analysis.The approach described has been used to study the partial contributions of inter-and intraband electron scattering events to the overall electron–phonon coupling in Al,Au,and Cu.87,88

Based on the presented experimental and theoretical results,we summarize that TTM can give a fairly correct description of electron–phonon coupling after electron thermalization,as it uses appropriate temperature dependences for the electron capacity Ceand parameter G.

VI.FOUR-TEMPERATURE MODEL FOR IRRADIATION OF AN NP BY FEMTOSECOND LASER PULSES

The theoretical four-temperature model(FTM)can be applied to describe laser-induced thermal processes in electron and lattice subsystems and in spherical metallic NPs when irradiated by femtosecond or picosecond pulses.The system of equations describing the thermal processes in electron and lattice subsystems and the NP as a whole,including thermal processes due to the irradiation of metal NPs by femtosecond laser pulses and also incorporating the results in Refs.7,8,12,and 89–91,has the form:

with the initial conditions:

V0and T0are the volume of the NP and the uniform temperature of the NP metal over its volume,respectively.c0andρ0are the heat capacity and density of the metal.N0is the NP concentration.qabsis the laser power density absorbed by the electron subsystem of the metal NP.qCis the heat power transferred from the metal NP.Cmand Tmare the heat capacity and temperature of the surrounding medium.The other terms have been define previously.

Equations(8)and(9)are used after the electron and lattice temperatures have become equal.Equations(6)and(7)describe the energy exchanged between electrons and phonons.They incorporate the heating of electrons by the laser pulse but not the energy lost from the NP.Equation(8)describes the cooling of the NP,whereas Eq.(9)describes the heating of the surrounding medium except for thermal losses.Equation(8)should include any possible thermal exchange between the NP and its surroundings by conduction,90melting,13,27,66or evaporation(ablation)17,18,20,27,92,93to correct the NP temperature in some threshold conditions.Equation(9)should include possible heating of the medium by a hot system of NPs,90bubble formation,24,25,29or other thermal processes.

The interaction of a femtosecond pulse with metal NPs reveals a number of nonlinearities associated with the strong nonequilibrium excitation of the electron gas followed by lattice excitation.The nonlinearities are affected by the dependences of the electron heat capacity Ceand the electron–phonon coupling factor G on the electron temperature.The characteristic parameters in the irradiation of metallic NPs by ultrashort laser pulses,such as the characteristic time of electron thermalizationτee,the electron heat capacity Ce(Te),and electron–phonon coupling G(Te),must be determined experimentally or theoretically independently of this approach.The time dependences of temperatures Te,Ti,T0,and Tmare determined by solving Eqs.(6)–(9).These temperatures can be used to describe the effect of a femtosecond laser pulse on a metal NP.Note that solutions of Eqs.(8)and(9)for T0and Tm,including expressions for qC,are presented in Ref.90.

Several approaches have been used in formulating FTM.The temperatures Te,Ti,and T0are assumed to be uniform inside the NP volume and are based on the homogeneous absorption of laser energy.If the NPs are sufficientl small compared to the wavelength and focal size of the heating laser beam,then the heating of the particle will be approximately uniform.94This has been confirme by computer modeling of an approximately homogeneous internal distribution of laser intensity inside gold and silver NPs with radii in the range 5–25 nm for widely used wavelengths such as 400,532,and 800 nm.95,96Thus,the electron and lattice temperatures can be considered uniform over the entire volume of the particle.Additionally,the characteristic time tTrequired for the formation of a quasi-uniform temperature profil inside the NP is estimated as tT≈r02/4χe,whereχeis the coefficien of electron thermal diffusivity for a metal.26This assumption if fulfille at t＞tT.For example,for a gold NP with r0≈30 nm andχe≈1.27 cm2s−197then tT≈1.4×10−12s,which means that the electron temperature in the volume V0is uniform over the pulse duration tP≥tT.Note that if there is strong heating of the electron subsystem Te≫Ti,the coefficien of electron diffusivity is much larger and the time tTwill be smaller.The speeds up the establishment of a uniform temperature inside the NP.For NPs with a larger radius,the intensity distribution inside them can be inhomogeneous,which should be accounted for in the time intervalτee≥t≥tP.On the other hand,thermal conduction inside the NP volume was neglected under the action of a femtosecond pulse.12,43,44,57

Several characteristic times determine the intervals during which various processes occur(or time when they end)after the irradiation of a metal NP by a femtosecond laser pulse:

(a) The heating of the electron subsystem by the laser femtosecond pulse with duration tP≈10−14to 10−13s.

(b) The thermalization of the hot electron subsystem occurs untilτee≈10−13s.The electron temperature is equilibrated by electron–electron scattering and electron–NP surface collisions.42–50

(c) Electron–phonon coupling occurs until characteristic timeτeph≈10−11to 10−12s.51–64

(d) The NP eventually relaxes back to the ambient temperature due to thermal conductivity.The characteristic time for NP cooling to occurτ0≈10−10to 10−9s depends on the NP radius r0and the surrounding medium.90

These times satisfy the following inequalities:

After the irradiation of an NP by an ultrashort laser pulse,these processes occur sequentially.Since they do not overlap,they can be studied separately.The large differences between these characteristic times allow different approaches to be used to simplify the system of Eqs.(6)–(9).The fina temperature at the end of one process can be used as the initial value for the subsequent process.

The excitation of plasmonic NPs by ultrashort laser pulses triggers a complex ultrafast relaxation process,which includes a gradual re-equilibration of the electron gas,lattice,and environment.One of the maim problems in studying these processes is the lack of direct experimental measurements of the evolution of the dynamic temperature of subsystems during and immediately after the pulse.Analytical solutions of Eqs.(6)–(9)have been produced to overcome this problem,and these are very convenient for analyzing and comparing analytical values with experimental results.

A.Heating of electrons in metallic NPs by an ultrashort pulse during the time intervaltP≥t≥0

Electrons in a metallic NP absorb the laser energy during the time interval tP≥t≥0 and are heated to their maximum temperature Tem.It is assumed that Tecan be used to characterize the electrons during the heating,although the electrons are in a nonequilibrium state during the irradiation.The duration of the femtosecond laser pulses tP≈10−14to 10−13s is shorter than the timeτeph≈10−12s of the electron–phonon coupling.51–64Thus,electron–phonon coupling can be neglected.During the femtosecond pulse,only the absorption of laser energy by electrons and partial electron–electron thermalization are considered.The temperature of the electrons can reach up to tens of thousands of kelvins,while the lattice remains cold.Other processes commence only after the end of the laser exposure.The heating is described by the following equation,which was derived by simplifying Eq.(6)without accounting for electron–phonon coupling:

and I is the laser intensity.S0and r0are the surface area and radius of a spherical NP.Kabsis the absorption efficienc for radiation with wavelengthλby an NP with radius r0.94In principle,the factor Kabscan depend on Teas Kabs(Te)=K∞Tne.A similar power law for Kabsand the temperature T0of a metal NP was used in Ref.98.The value of Temdoes not depend on the temporal form of I(t)due to the absence of heat losses during the time tP.Thus,a constant value of I can be used to solve Eq.(12).Solving Eq.(12)using Ce(Te)=γTαe,Kabs(Te)=K∞Tne,and a constant value of I gives the maximum value of Temat t=tP:

T∞is the initial temperature of the NP electrons and medium and E=∫0tpI(t)dt is the laser fluence The dependence of the electron capacity on temperature Ce(Te)=γTe(α=1)is most applicable for relatively low electron heating of up to 3×103K.

For a sample consisting of gold nanospheres 100 nm in size,the electrons were heated up to Te≈2×103K under pump pulses with a central wavelength of 785 nm and a duration of about 350 fs with a pulse energy up to～2 pJ.50The nonlinear relation between Teand the pulse energy,shown in Fig.7 by the dotted line,is close to Eq.(13b),so that it can be used in this temperature interval.

The duration of the femtosecond and picosecond laser pulses is tP≈10−12to 10−11s,which is long compared with the characteristic times for electron–phonon couplingτeph≈10−12to 10−11s and electron thermalizationτee≈10−12s.For a picosecond pulse irradiating a metal NP,absorption by electrons,electron thermalization,and electron–phonon energy coupling occur simultaneously during and after the pulse asτeph≥τee≥tP＞t＞0.For powerful heating,the condition Te≫Timay be fulfille and Tican be neglected compared to Te.Thus,the system of Eqs.(6)and(7)with G(Te)=G1Tethen has the form:

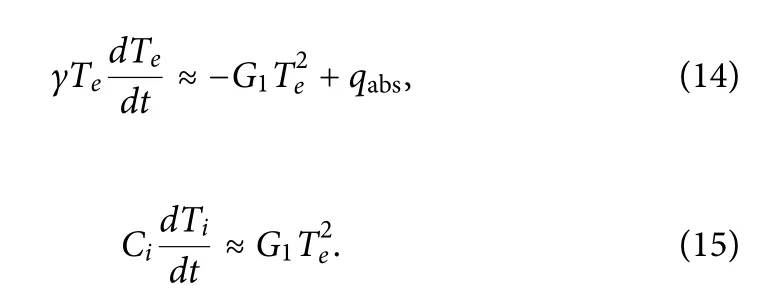
FIG.7.Electron temperature plotted againstpulse energy.The dotted gray line has a slope of 1.Adapted from Ref.50 with permission from ACS.

It is possible to get solutions to Eqs.(14)and(15)for constant I during a picosecond pulse:

which can be used to describe the increase of Teand Tidue to irradiation of a picosecond pulse on an NP and accounts for the energy exchanged between electrons and phonons.

B.Electron thermal equilibration in the time intervalτee≥t＞t P

Obviously,electron thermal equilibration begins after the end of the pulse and completes during the time intervalτee≥t＞tP.It is assumed that at the moment t≈tP+τee,the electron and lattice subsystems are in thermal equilibrium at temperatures Temand T∞,respectively,and that no energy is transferred from the electron subsystem to the lattice during this interval.

C.Electron–phonon coupling in the time intervalτeph≥t＞t P+τee

Electron–phonon coupling and the dynamics of Teand Tistart when the electrons are in thermal equilibrium.The electron temperature is then a maximum Tem,and the lattice temperature is equal to the initial temperature T∞.The hot electrons cool down by transferring their energy to the lattice via electron–phonon coupling.The equalization of Teand Tithrough electron–phonon coupling occurs roughly during the intervalτeph≥t＞tP+τee.By t≥tP+τee+τeph,then Te=Ti=Teq,so that the total equalized temperature T0=Teqcan be used for the entire NP volume as the initial condition for the following process.

Temperature relaxation and electron–phonon coupling have been investigated with the two-coupled kinetics of Eqs.(6)and(7)but without considering the absorption of energy qabs,which by this stage is complete:

The initial conditions for Eq.(17)at a formally define moment t=0 are as follows:

The equalized temperature Teqof the electron–lattice system after the termination of the energy exchange between electrons and lattice is

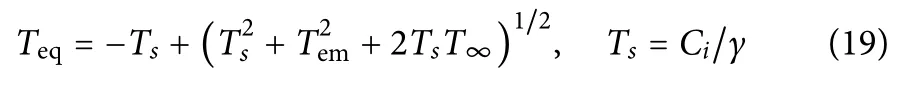
The value of Teqis determined from the law of conservation of energy applied to the electron–phonon coupling.The lattice temperature can,thus,be determined:

A significan increase of the calculated values of G(Te)and Ce(Te)for gold,silver,copper,and tungsten,based on first principles calculations and accounting for the thermal excitation of the electrons,has been found for temperatures up to 2×104K51,67–69,75,82and also above.The theoretical values of Ce(Te)and G(Te)for gold(silver,copper,and tungsten)51can be approximated by linear relations:89

with G1≈1.2×107W/cm3K2andγ1≈1.65×10−4J/cm3K2for gold.89As noted earlier,the approximation in Eq.(4),Ce(Te)≈γ1Te,can be used for temperatures up to～3×103K.Moreover,the approximations in Eq.(21)can be used for a wider temperature range of up to(1–2)×104K with appropriate accuracy,ifγ1and G1can be determined from the linear approximations of the theoretical Ce(Te)and G(Te).51,67–69,75,82The analytical solution of Tein Eq.(19)has the following form,89which incorporates Eq.(21):

Equation(20)is the solution for Ti(t).The values of Tsand Teqin Eq.(22)can be determined from Eq.(19)using the given value of γ1.Note that the temporal evolution of the electron temperature in Eq.(22)is not a direct exponential decay Te(t)≈exp(−t).However,a combination of terms in Eq.(22)are exponential decays with a characteristic time for electron–phonon coupling:

The analytical solution in Eq.(22),which incorporates the temperature dependences of the parameters G(Te)and Ce(Te),can be used to describe the interaction between an ultrashort pulse and metal NPs(gold and the above metals)over a wide temperature interval for the hot electrons.

A linear relation for Ce(Te)and a constant value for the coupling parameter G:

have been applied to fin a solution to Eqs.(6)and(7),which has the form:58,89

Here,G2=2.1×1010Wcm−3K−1andγ2=6.79×10−5J cm−3K−2for gold.89The values of Tsand Teqin Eq.(24)can be determined from Eq.(19)using the given value ofγ2.In this case,some complex combination of terms,which includes Te,decays exponentially with the characteristic electron–phonon coupling time:

The relation Ce=γTeand constant G have been used in numerical calculations of the electron–phonon coupling in NPs.60,99–101

The relations for G(Te)and Ce(Te)for nickel and platinum51,68have been approximated as being inversely or directly proportional to the temperature,respectively:

These simple approximations have relative deviations of the order of 10%–20%51,75for the temperature interval 3×103to 2×104K.Solutions of Eqs.(11)and(12)using Eq.(25)have the form:

The values of Tsand Teqin Eq.(26)can be determined from Eq.(19)using the given value ofγ3.The electron temperature then decays nonexponentially.

A significan increase in the electron–phonon coupling and electron heat capacity can lead to different sequences in the processes affecting the electron temperature.This usually occurs via femtosecond or subpicosecond laser–metal interactions.An increase or decrease in the rate of energy transfer from hot electrons to the lattice can lead to a change in the timescales of and relations for laser-induced transformations.

It is interesting to compare the influenc of Eq.(22),which has G1andγ1,and Eq.(24),which has G2andγ2,12,53on the maximum electron temperature Temfor gold.The characteristic times of the electron–phonon coupling and the equalized temperatures for these cases are,respectively,

with T1eqand T1sdetermined from Eq.(19)withγ1and

with T2eqand T2sdetermined from Eq.(19)withγ2.

FIG.8.(a)T1eq(red line,1)and T2eq(blue line,2)vs T em determined using Eq.(21)withγ1 andγ2.(b)Characteristic timesτ1eph vs T em determined using Eq.(22)with γ1 and G1(red line,1)andτ2eph vs T em determined using Eq.(24)withγ2 and G2(blue line,2).Values are for a gold NP.Adapted from Ref.91.

FIG.9.T e(solid lines)and T i(dashed lines)vs t determined using Eq.(22)withγ1 and G1(red lines,1)or Eq.(24)withγ2 and G2(blue lines,2)for T em=1×104 K.Adapted from Ref.91.

The equilibrium temperatures of an electron–lattice system T1eqand T2eqare much lower than the maximum temperature of the electron subsystem Tem[Fig.8(a)].This difference is due to the corresponding difference in the heat capacities of the electron gas Ceand the lattice Ci.Consequently,the energy stored in the electronic subsystem at Temis sufficien to heat the lattice only to temperatures lower than Tem.On the other hand,the difference between T1eqand T2eqfor a given value of Temis due to the difference between the values ofγ1andγ2used,especially as Temincreases.According to Fig.8,the temperature of an ionic subsystem when Tem＞1×104K can be higher than the melting temperature.However,the effect of the latent heat of NP melting and the dependence of this heat on the ionic temperature are not accounted for.It is possible that accounting for the melting would decrease the temperature of the ionic subsystem.

The timesτ1ephandτ2ephdepend on Teqand Temin opposite ways.Thus,τ1ephdecreases andτ2ephincreases with increasing Teqor Tem.These times are approximately equal to each other at Tem≈2×104K.Note that it is difficul to extract a value forτephonly from experimental data.The experimental method described in Ref.61 was used to extract the experimental ultrafast temperature evolution of plasmonic Au NPs with an average size of 20–25 nm as a function of time.The energy exchanged between the population of excited electrons and the NP lattice via electron–phonon coupling led to thermalization in the timescaleτeph≈10–30 ps,61which is consistent with line 1 in Fig.8(b).

The temperature Tedecreases and temperature Tiincreases over time due to the heat exchanged between the hot electrons and the cold lattice(Fig.9).The temporal evolutions of Teand Tihave a complex form determined by the nonexponential solutions of Eqs.(22)and(24).Energy transfer between electrons and phonons terminates when the temperatures are equal:Te=Ti=Teq2=1.5×103K and Teq1=3.1×103K,respectively,for Tem=1×104K.

The electron–phonon coupling and the corresponding energy exchange have been studied experimentally and using ab initio theory for nonequilibrium states of the free-electron metal aluminum.73Pump pulses centered at 800 nm with a duration of about 50 fs were used to photoexcite freestanding 30-nm-thick film of polycrystalline aluminum.The strength of the electron–phonon coupling was obtained for a range of electron and lattice temperatures from a molecular dynamics simulation based on density functional theory.The electron–phonon coupling parameter,extracted from the experimental data using TTM,deviated significantl from the ab initio values.

For all excitation densities,TTMcan reproduce the time dependence excellently using the fitte coupling parameters,as shown in Fig.10(a).The increase of Gepwith uEsuggests that there is a significan dependence of Gepon Te,as introduced in Ref.51.The dependence of the coupling parameter Gepon Tewas incorporatedinto TTM,as shown in Fig.10(a).This experiment confirme the need to consider the dependence of G on Teif the theory is to agree with the experimental evolution of Teand Tiover time.

FIG.10.(a)Measured lattice temperatures(circles)and lattice temperatures simulated with TTM with optimized parameters for three different absorbed energy densities uE.The lower part ofthe panelshows the residuals for the highest excitation density.(b)Electron–phonon coupling parameter G ep vs the absorbed fluence uE.(c)Electron–phonon coupling parameter vs electron temperature obtained by measurements.The green line shows G ep(T e)obtained from density functionaltheory.The dashed light green line is from Ref.51.Adapted from Ref.73 with permission from APS.

D.CoolingoftheNPsandheating ofthesurroundingmediuminthetimeintervalt≥τ0

At the moment t＊when the temperatures are equal Te=Ti=Teq,the temperature of the NPs and the medium are,respectively,T0＊=Teqand Tm=T∞.The cooling of the NPs and the heating of the surrounding medium due to energy exchange with the NPs for t＞t＊are described by Eqs.(8)and(9)with solutions:90

where c andρare the heat capacity and density of the surrounding medium,respectively.Tmis the temperature of the medium in an infinitel small volume containing one NP.

VII.ANALYTICALDESCRIPTIONOFTHEEFFECT OFAFEMTOSECONDPULSEONAMETALNP

Using the theory presented,the effect of a femtosecond pulse on a metal NP is described analytically from the start of the laser pulse to the completion of the cooling of the NP down to the initial ambient temperature.Equation(12)makes it possible to calculate the maximum electron temperature Temfor specifi laser and NP parameters and to estimate the electron-thermalization time.This temperature can be used as the initial value for the electron–phonon coupling in the solutions in Eqs.(17)and(18)up to the time t＊,which is consistent with the equalization of the electron and lattice temperatures Te=Ti=T0＊.Subsequently,the NP temperature T0is used.Temperatures T0＊and T∞are used as initial values when calculating the cooling of the NP and the heating of the medium with Eq.(27).Possible convection and overheating of the surrounding liquid were not accounted for since the time interval is short and because the liquid temperature does not exceed the critical water temperature.

FIG.11.Analytically calculated time evolution of the electron temperature T e(solid red lime),NP lattice temperature T i(dashed red line),NP temperature T0(dotted red line),and water T m(blue dashed-dotted line)for a gold NP with a radius of 20 nm after irradiation by a femtosecond pulse with a duration of 150 fs,wavelength of 400 nm,and laser fluence of 14.5 mJ/cm2.

The time evolution of the temperatures of the electrons,lattice,and water for a gold NP with a radius of 20 nm under the action of a femtosecond pulse with a duration of 150 fs,a wavelength of 400 nm,and a laser fluenc of 14.5 mJ/cm2were calculated analytically,as shown in Fig.11.The maximum electron temperature Tem=1×104K from Eq.(17).The melting of the NP was accountedfor when the melting temperature of gold was achieved,as indicated by a small step in the curve for Ti(t)in the time interval 0–25 ps.The evolution over time of the electron temperature,the lattice temperature(NP temperature for t＞t＊),and the water temperature(Fig.8)qualitatively agree well with the results of computer calculations,60,98which confirm the validity of the presented analytical model.

The sequence of actions due to irradiation by an ultrashort laser pulse on a metal NP is presented in Table I along with the characteristic start and end times of the corresponding processes.Note the time intervals for thermal confinemen in the electron and lattice subsystems.The confinemen of thermal energy in a hot electron gas with a temperature～Temoccurs for a timeτee≈1×10−13s＜t＜τeph≈1×10−11s.During this time,the hot electrons could be used for various applications.In the time intervalτeph≈1×10−11s＜t＜τ0≈1×10−9s,the NP energy is confined Approximately all of the NP thermal energy is inside the NP and there are only small heat losses due to thermal conduction.This energy could be used to initiate processes inside the NP and in the surrounding medium.

TABLE I.Action of an ultrashort laser pulse on a metalNP.

VIII.CONCLUSIONS AND APPLICATIONS

The interaction of femtosecond pulses with metals and metallic NPs has been widely investigated.There have been recent applications in photonics,photochemistry,laser processing of metallic nanostructures,etc.After the ultrafast deposition of high-density energy,the metal enters a nonequilibrium high-temperature state,which induces an equilibrium in the of temperature of the electrons,an exchange of electron energy with the lattice(ions),and the evolution of material properties,phase transitions,and subsequent processes.

TTM was proposed by Anisimov et al.7to provide a theoretical description and understanding of experimental processes and results.TTM is still widely used.The exchange of electron energy with the lattice is commonly described by TTM based on the assumption that the population of electron and phonon states can be separately described by the electron temperature Teand the lattice temperature Tiand by two coupled differential equations for the heat exchanged between electrons and phonons.A detailed understanding of the energy transfer between hot electrons and the lattice at high temperatures provides insights into the relations between the optical response and the temperature of the nanosystem.TTM is suitable for describing metals excited by a laser on timescales from a few hundreds of femtoseconds to tens of picoseconds with adequate accuracy,as demonstrated by various experiments.TTMhas been widely applied in studying laser–matter interactions and in describing laser material processing.Today,it remains one of the most commonly used computational tools in the community due to its simplicity.However,the results from pump–probe and other experiments need to be converted to electron and ion temperatures,and this process usually depends on the model(TTM).New experimental techniques are needed such that the results can be directly compared with theoretical data.Experimental and theoretical results for the relations between and the values of the main parameters in the interaction of a femtosecond pulse with a metal,such as the electron-thermalization timeτee,the electron heat capacity Ce,and the electron–phonon parameter G,for various conditions and metals,were used to formulate the model.In TTM,a linear relation between Ceand Teand a constant value of G are usually used for the narrow temperature range Te≈300 to 3×103K.

Recently,high-temperature laser and photonic nanotechniques have been actively developed for applications in laser metal processing,laser photocatalysis,optoelectronics,photodetection,devices for hot electron generation and injection,etc.These applications require experimental and theoretical investigations of the temperature dependences of Ce(Te),G(Te)and other thermooptical parameters for electron temperatures up to Te≈2×104K or higher.Experimental investigations in these temperature ranges are especially significant since practically no such experiments have been done.Theoretical studies based on firs principles and the density of electron states have determined the nonlinear dependencies of Ce(Te)and G(Te)on temperature.One of the goals of our review was to present the temperature dependences of Ce(Te)and G(Te)based on the available theoretical and experimental data and to explain and describe electron–lattice thermal processes.So far,Ce(Te)and G(Te)have been calculated at elevated electron temperatures only for a few metals,but the values for each parameter differ for each metal and are urgently needed for a variety of metals.

Recently,studies of the effect of femtosecond laser pulses on metal NPs have been carried out with FTM(Te,Ti,the NP temperature T0,and the temperature Tmof the surrounding medium),an overview of which is presented here.The entire femtosecond heating of an NP and subsequent thermal processes can be divided into four stages:(1)heating of the electron system by the femtosecond pulse,(2)electron thermalization,(3)energy exchange between electrons and phonons and the equalization of the temperatures of the electrons and the lattice to the NP temperature,and(4)energy exchange between the NP and the surrounding medium,the cooling of the NP,and subsequent processes.FTM assumes that,for an ultrashort laser excitation,the above processes are separate in time and can,therefore,be studied separately(Table I).The fina temperature at each stage is used as the initial condition for the next stage.Thus,the main difference between TTMand FTMis that FTM can describe the entire process,beginning with the absorption of laser energy by electrons and all subsequent processes.For various metals,linear relations for Ce(Te)and G(Te)with temperature and an inversely linear relation for Geph(Te)with temperature were used.All these assumptions lead to an appropriate simplificatio of the general system of equations so that we can obtain analytical solutions for each time stage and for the overall process.Some of our analytical results are presented in this review.Analytical solutions of the equations were used to describe satisfactorily the action of a femtosecond pulse on an NP and to estimate the main parameters in the process.Our analysis of the results clearly demonstrates the influenc of the dependences on temperature of Ce(Te)and G(Te)on the quantitative values of the interaction parameters and the temperature and time dependences.A qualitative and quantitative comparison with computer results for femtosecond pulses showed satisfactory agreement and validated the analytical approach used.Moreover,these results can partially be used for picosecond laser pulses.The advantage of FTMin comparison with other models and computer calculations lie in its simplicity.FTMcan be used to obtain analytical solutions with universality,clarity,and sufficien accuracy for a theoretical description of the action of ultrashort laser pulses on metal NPs and to determine the dynamics of Teand Tineeded to understand the results of experiments.

A description and analysis of the results of such interactions are very important for successful applications of femtosecond lasers used to irradiate NPs.These applications utilize the generation,emission,and transfer of hot electrons from plasmonic metal NPs to surface adsorbates and adjacent semiconductors,in photodetectors,photocatalysts,biosensors,and chemical sensors.

Recently,ultrashort laser processing of metals and metallic nanostructures has been intensively developed.The processes that occur after the irradiation of an ultrafast laser on metals(NPs)include the absorption of light by the electrons in the skin layer,energy transfer from the skin layer to the target interior by nonlinear electronic heat conduction,the relaxation of the electron and ion temperatures,ultrafast melting,the formation of metastable states,and the hydrodynamic expansion of the heated matter.Innovative laser nanofabrication and processing techniques can produce spherical NPs,nanorods,and nanoprisms.In such processes,controlling the morphology of the heated and melted gold nanosphere aggregates is very important.Measurements of the dynamics of silver melting after excitation with a femtosecond laser revealed a two-stage process,due to the extreme electron temperatures attained.Within a few picoseconds,the electron and phonon systems begin to equilibrate and the thin surface layer melts.During this period,the thermal conductivity is strongly suppressed.102Carefully choosing the laser fluenc and wavelength of a femtosecond laser makes it possible to selectively excite different aggregate substructures,resulting in the spatial extension of NP ensembles.This allows us to control the morphology of the nanostructures formed after melting.103It has been experimentally established that,at low energy densities,a low ion heating rate allows a solid–liquid phase transition to occur in the form of heterogeneous melting initiated at the sites of liquid nucleation on the surface,grain boundaries,or defects.66However,higher energy densities can cause extremely high heating rates in excess of 1014K/s,creating an overheated state in which homogeneous nucleation occurs throughout the sample.

After ablation by an ultrashort laser pulse,various types of phase transitions occur:melting,vaporization,transition to warm dense matter,and nonthermal phase transitions.These are directly caused by the electronic excitation until the lattice becomes significantl hot.104Laser ablation through a liquid is an important process for applications that use laser ablation and shock peening.Molecular dynamics simulations show that NPs form as a result of vapor condensation in a cold liquid and in an atomic mixture of metal and liquid.105The fina removal of material occurs due to the expansion of heated metal,which can be described by two-temperature electron–ion hydrodynamics,by analyzing the dynamics of the excited electrons and the structural dynamics,as well as by molecular dynamics simulations.The melting,evaporation,and ablation of NPs by ultrashort laser pulses are being actively developed and widely applied in laser nanotechnology.Such innovative techniques have considerable promise.

The generation of nonequilibrium hot carriers has attracted intensive research attention in the last decade,both because of the fundamental aspects of extreme light–matter interactions and because of the potential practical applications.The generation,survival,and extraction of hot electrons from the surface of metallic materials and plasmonic nanostructures with energies well above the Fermi level present a variety of new challenges and opportunities,including energy harvesting and conversion,photocatalysis,optoelectronics,photodetection,photochemistry,and chemical sensors.106–109Plasmonic metal nanostructures can absorb laser light(or light in an extended spectral range)and transfer the absorbed light energy to adjacent molecules or semiconductors,enhancing the charge separation and migration in the semiconductor as a“plasmonic photosensitizer.”The mechanisms of hot electron transfer from the plasmonic metal to surface adsorbates or to adjacent semiconductors have been described.The plasmon enhances photoconversion in a metal–semiconductor heterojunction via light scattering or trapping,plasmon-induced resonance energy transfer,and hot electron injection.To achieve effective utilization of the hot carriers,three conditions must be fulfilled (1)the incident light must efficientl excite the hot carriers in a metal nanostructure,(2)the plasmonic hot carriers must be efficientl separated and extracted before they cool to an equilibrium state,and(3)recombination,including thermal relaxation and charge back transfer,must be suppressed.For example,Au NPs,which have optimal sizes in the range 10–20 nm for efficien photon-to-electron conversion and generation of hot carriers,were embedded at a hole conductor/semiconductor interface,110where they served as photosensitizers.The hot electrons were injected into TiO2,and the hot holes were transferred to the hole conductor.The behavior of hot electrons determines the properties of optically excited materials at very short timescales,such as between femtoseconds and picoseconds,which opens up the possibility of their use in devices with a short response time.The time interval between τephandτeedetermines the possibility of confinin the electron energy.The electron energy stored up to that moment can be used to emit electrons from the rear hemisphere of an NP when its front hemisphere is irradiated.The inhomogeneous distribution of the laser energy absorbed by electrons and their heating inside the rear hemisphere of the NP volume95,96can be used to inject hot electrons from the rear surface of the NPs after irradiation by a femtosecond laser.A detailed understanding of the generation of plasmonic hot carriers and,in particular,the transfer that occurs at metal–semiconductor interfaces was presented in Ref.111.

Chemical reactions can be directly photocatalyzed on the surface of a plasmonic metal nanostructure by excited hot carriers.Such a plasmonic metal nanostructure with excited hot carriers can also serve as a photosensitizer with a semiconductor to enhance the photocatalysis.112–114Hot-carrier injection induces various physicochemical processes,such as molecular dissociation,desorption,and chemical reactions.113Plasmon-generated hot carriers can be used to drive chemical reactions,which makes it possible to control the selectivity of a reaction,in contrast to temperature-driven catalysis.Photocatalysis based on the plasmon-induced transfer of hot electrons has been widely developed.The architecture of a plasmonic nanoelectrode has been proposed.This electrode can inject bunches of hot electrons into an aqueous environment due to multiphoton absorption,acceleration by ponderomotive forces,and electron–water interactions through random elastic and inelastic scattering.109In this approach,electrons are accelerated in water by the ponderomotive forces to energies capable of exciting or ionizing water molecules,which has been confirme by observing the bubbles generated for a laser power exceeding the corresponding threshold.Molecular dynamics and two-temperature hydrodynamics codes are used to describe ablation into a liquid and,in combination with thermodynamic information(such as the equation of state of matter),allows one to estimate the mass and composition of NPs formed under laser exposure.115Due to their high kinetic energy and large reduction potential,wet hot electrons could open up new opportunities in photocatalysis,electrochemical processes,and hot-electron driven chemistry.Various possible applications of hot electrons of practical interest have also been investigated.116–118In general,the results presented in this review can be applied to the design of both purely solid-state opto-electronic devices and photocatalysis and energy conversion systems.

ACKNOWLEDGMENTS

This work is supported by the Belarusian state program for scientifi investigations“Convergence”(Grant No.N 2.2.02).

AUTHOR DECLARATIONS

Conflict of Interest

The author has no conflict of interest to disclose.

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.