路矩阵的谱及两类组合图的路谱

卢鹏丽， 栾睿， 郭育红， 陈娅红

(1.兰州理工大学 计算机与通信学院，甘肃 兰州 730050； 2.河西学院 数学与统计学院，甘肃 张掖 734034； 3.丽水学院 数学系，浙江 丽水 323000)

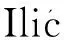
1 基本概念和主要引理

本文中只讨论简单连通图，设图G=(V(G),E(G))，其中顶点集和边集分别为V(G)={v1,v2, …,vn}，E(G)={e1,e2,…,em}。图G的路矩阵记为P(G)=[pij]n×n，其中pij=pG(vi,vj)表示顶点vi和vj之间的顶点不相交(即不重复)路径的最大数目。因为路矩阵为实对称矩阵，因此其特征值均为实数，记为ρ1(G)≥ρ2(G)≥…≥ρn(G)，路特征值的集合称为图G的路谱，ρ1(G)为图G的路谱半径。ρ1(A)表示为矩阵A的最大特征值。图G的路谱能量[2]定义为：

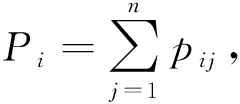
图G1和图G2的联图G1∨G2是指将图G1中的每个顶点与图G2中的每个顶点相连而得到的图。图G1和图G2的冠图G1∘G2是将图G2复制|V(G1)|次，然后把G1中第i个顶点与第i个G2的所有顶点相连接而得到的。

引理1[12]Perron-Frobenius定理：设A为n×n阶非负不可约矩阵且n≥2，则

1)A的谱半径μ(A)是正数；

2)A的谱半径μ(A)是代数单重特征值；

3)存在唯一的实(列)向量x=[x1x2…xn]T使得Ax=μ(A)x且x1+x2+…+xn=1，这个向量的所有分量元素为正的；

4)存在唯一的实(列)向量y=(y1,y2,…,yn)T使得yTA=μ(A)yT且x1y1+x2y2+…+xnyn=1，这个向量的所有分量元素为正的。

引理2[13]令π：V(G)=V1∪V2∪…∪Vk为连通图G的路等价划分，Qπ和P(G)分别为图G的路商矩阵和路矩阵。如果α是Qπ的特征值，则α也是P(G)的特征值。

2 路谱半径和路谱能量

引理3n个顶点的连通图G只有2个不同的路特征值当且仅当G是k-连通且k-正则图，2≤k≤n-1。

证明：令连通图G的路矩阵为P(G)，假设G恰有2个不同的路特征值：λ1，λ2，且令λ1>λ2。因为G为连通图，则P(G)为不可约矩阵，由引理1可知，λ1为P(G)的最大单特征值，因此λ1的重数为1，λ2的重数为n-1。现在证明P(G)=k(J-I)。

设与λ1对应的特征向量为p1，与λ2对应的n-1个线性无关的特征向量为p2,p3,…,pn，将p1,p2，…,pn正交化单位化得到向量ξ1,ξ2,…,ξn，记C=(ξ1,ξ2,…,ξn)，C为正交矩阵，且

因此

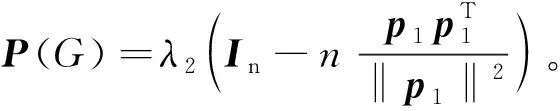
令p1=(x1,x2,…,xn)T，则

因为P(G)的对角线全为0，因此：

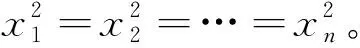
由上面讨论可知λ2<0，又因为路矩阵的定义，其中的元素代表两顶点间不相交路径数目最大值，所以-λ2为正整数，由此可证G为k-连通且k-正则图。

反之，假设G为n阶k-连通且k-正则图，则P(G)=k(J-I)，则该矩阵恰有2个不同的路特征值：k(n-1)和-k，分别对应的重数为：1和(n-1)。该定理得证。

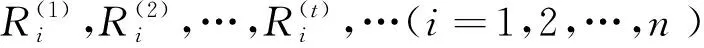
(1)

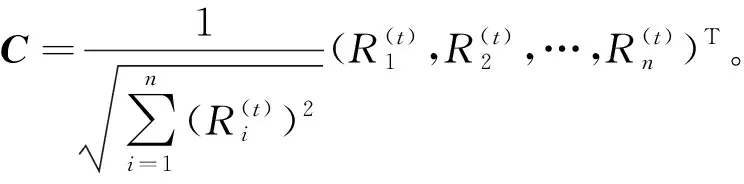
因为C是单位向量且分量元素都为正数，因此有：

因为PC=

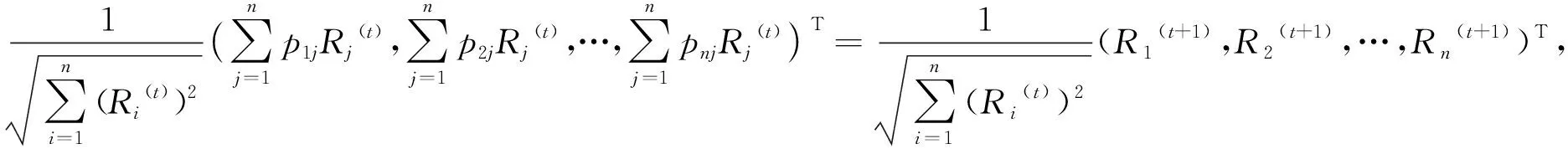
(2)

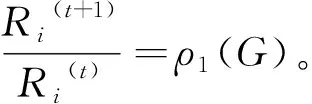
例1图1所示为a+b+c个顶点的双圈图B(a,b,c)，其路矩阵可以表示为：

图1 双圈图Β(a,b,c)Fig.1 Bicycle graph Β(a,b,c)

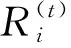
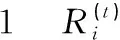
表的值

由表中数据和定理1可知，当t=1时，ρ1(Β(3,4,2))≥10.132 023 230 176 790，当t=2时，ρ1(Β(3,4,2))≥10.132 531 267 946 458，当t=3时，ρ1(Β(3,4,2))≥10.132 543 826 615 851，当t=4时，ρ1(Β(3,4,2))≥10.132 544 092 795 836，当t=5时，ρ1(Β(3,4,2))≥10.132 544 098 202 750，当t=6时，ρ1(Β(3,4,2))≥10.132 544 098 310 817，当t=7时，ρ1(Β(3,4,2))≥10.132 544 098 312 961，当t=8时，ρ1(Β(3,4,2))≥10.132 544 098 313 003。

当t变大时，双圈图Β(3,4,2)对应路矩阵的谱半径的下界会越来越精确。

推论1令G为n个顶点的连通图，其对应的路度序列为{P1,P2,…,Pn}，第二路度序列为{T1P,T2P,…,TnP}，则

当且仅当G为伪路正则图时等号成立。

证明：由定理1可知，在式(1)中，当α=1，t=1时得证。

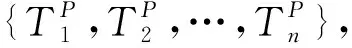
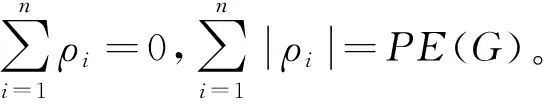
(PE(G)-ρ1)2≤(n-1)(S-ρ12)

(3)

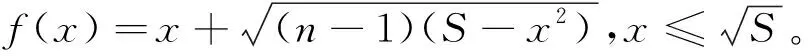
|ρ2|=|ρ3|=…=|ρn|⟹

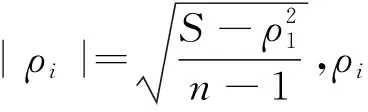
2)G恰有2个完全不同的路特征值，则由引理3，G为k-连通且k-正则图。

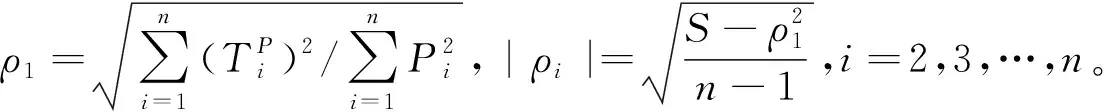
下面证明k-连通且k-正则图的两类组合图的路谱，采用2种方式求解其对应路矩阵的特征值，一种是求解路矩阵对应商矩阵的特征值，另一种是构造路矩阵特征向量的方式求解路矩阵的特征值。由于采用第1种方法求解联图G1∨G2时路商矩阵的阶数为二阶，求解其特征值时较为简单，因此在求解上述组合图的路谱时采用路商矩阵的方式。但在求解冠图的路谱时，当冠图中的顶点较多时，其对应的路商矩阵阶数较大，对于求解其路商矩阵的特征值较困难，因此采用构造特征向量的方式。

3 联图G1∨G2的路谱

定理3设图Gi为ni个顶点的ki-连通且ki-正则图，i=1,2。

1)若n1+k2>n2+k1，则图G1∨G2的路谱为：-(k1+n2)，重数为n1-1；-(k2+n1)，重数为n2-1；矩阵

的特征值。

2)若n1+k2≤n2+k1，则图G1∨G2的路谱为：-(k1+n2)，重数为n1-1；-(k2+n1)，重数为n2-1；矩阵

的特征值。

证明：1)由联图G1∨G2的定义可知，图G1∨G2的路矩阵可以表示为：

其中J是全1矩阵。由矩阵P(G1∨G2)可以很容易得到其n1+n2-2个特征值：-(k1+n2)，重数为n1-1；-(k2+n1)，重数为n2-1。矩阵P(G1∨G2)的商矩阵Q1为：

计算det(xI-Q1)=0，可得到Q1的特征值，由引理2可知，此特征值为矩阵P(G1G2)的剩余2个特征值，由此可证。

2)对联图G1∨G2的顶点进行适当编号，G1∨G2的路矩阵可以表示为：

证明方法同定理3中1)。

推论2设图G1是n个顶点的k-连通且k-正则图(1≤k≤n-1)，图G2是n-1个顶点的(k-1)-连通且(k-1)-正则图，则图G1∨G2是路整谱图，PE(G1∨G2)=4(n-1)(n+k-1)。

证明：由定理3中2)可得，n1=n，k1=k，n2=n-1，k2=k-1，则G1∨G2的路谱为：-(n+k-1)，重数为2n-2；2(n+k-1)(n-1)，显然，G1∨G2是路整谱图。由路谱能量的定义可得PE(G1∨G2)=4(n-1)(n+k-1)。

推论3完全二部图Kn1,n2(n1≤n2)的路谱为：-n2，重数为n1-1；-n1，重数为n2-1；矩阵

的特征值。

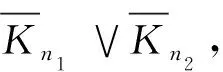
4 冠图G1∘G2的路谱

定理4设图Gi为ni个顶点的ki-连通且ki-正则图，i=1,2，ki≠0，则冠图G1∘G2的路谱为

1)-(k2+1)，重数为n1(n2-1)；

证明：由冠图的定义可知，图G1∘G2的路矩阵可表示为：

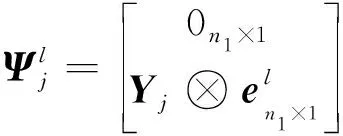
因此，-(k2+1)是矩阵P(G1∘G2)的特征值，重数为n1(n2-1)，定理4中的1)得证。

设Xi，i=2,3,…,n1是矩阵Jn1的特征值0所对应的特征向量，则Xi和全一向量正交。设μir，r=1,2是方程

x2-Ax+B=0

(4)

由Matlab求解上述方程组可得方程(4)，定理4中的2)得证。

到目前为止，共求得n1(n2-1)+2(n1-1)=n1(n2+1)-2个特征值，剩余2个。

因为矩阵Jn1的特征值n1所对应的特征向量为Jn1×1，其他所有的特征向量都和全一向量正交，所以剩余2个特征向量构造：

其中(α,β)≠(0,0)。设υ是矩阵P(G1∘G2)的特征向量Ω所对应的特征值，则由P(G1∘G2)·Ω=υ·Ω可得

设α≠0，否则求解上述方程组可得β=0，矛盾。因此，不失一般性，设α=1，用Matlab求解上述方程组可得定理4中的3)，证毕。

5 结论

1)本文得到了任意图的路矩阵的谱半径的下界，通过迭代次数的增加，其谱半径的下界越来越接近其真实谱半径的值；而利用路谱能量的上界可得到特定图的路谱能量的范围。

2)得到了k-连通且k-正则图的两类组合图(联图G1∨G2和冠图G1∘G2)的路谱。

3)得到了一类特殊路整谱图及其路谱能量公式，拓宽了路谱的研究范围。