CT数据一致性条件及其应用综述

汤少杰， 俞恒永， 牟轩沁

(1.西安邮电大学 自动化学院， 西安 710121; 2.西安机器人智能系统国际科技合作基地， 西安 710121; 3.马萨诸塞大学 洛厄尔分校电气与计算机工程系， 马萨 01854; 4. 西安交通大学 电子与信息工程学院， 西安 710121)

0 引言

当今计算机断层扫描(Computed Tomography, CT)技术在医疗、工业、安检等众多领域有着不可替代的作用。X射线CT技术的发展经历了长期的过程。1901年，第一个诺贝尔物理学奖因发现X射线被授予德国物理学家Röntgen(图1)。这是X射线CT技术的重要物理前提。

图1 (a)德国物理学家Röntgen;(b)其夫人左手X光照片

1917年,奥地利数学家Radon提出二维Radon变换及其逆变换[1]，成为现代CT重建理论的基础。1979年,诺贝尔生理学或医学奖因CT研发做出贡献被授予英国工程师Hounsfield[2]和美籍南非裔物理学家Cormack(图2)。

图2 (a)英国工程师Hounsfield；(b)美籍南非裔物理学家Cormack

在应用推动下，二维CT之后出现了多排CT，投影几何从二维平行束发展到等角扇束、等距扇束，扫描轨迹也从直线轨迹、圆形轨迹发展到一般轨迹。适应于多排CT的FDK近似重建算法在1984年由Feldkamp、Davis 、Kress 三人提出[3]。随着探测器工业的进步，多排CT之后又出现了锥束CT，同时，锥束重建理论也飞速发展。基于三维Radon变换及其逆变换，Tuy和Smith提出了作为锥束CT重建充要条件的Tuy-Smith完备理论及相应重建算法[4-5]。随后，基于三维Radon变换导函数，Grangeat提出了算法流程更为适用的锥束CT重建算法[6]。1993年，Wang等提出螺旋锥束CT成像方式及相应的近似重建算法[7]，2000年，Kachelrieß等提出了ASSR近似重建算法算法[8]。进入21世纪后，锥束CT重建理论研究迎来了关键时期。在此期间，三维FBP类型的Katsevich算法[9]以及三维BPF类型算法[10-12]相继被提出并实现，从而攻克了长久以来的难题——螺旋(甚至更为复杂扫描轨迹)锥束CT精确重建。

众所周知，CT成像包含了众多软硬件技术，任一部分的不完善都会导致CT重建图像中表现出伪影[13]，影响CT图像质量与后续诊断。对上述CT重建算法与伪影校正感兴趣的读者推荐深入研究本文相关参考文献[19-21]。

CT理论中还包含数据一致性条件方面的研究[22]。数据一致性条件有着非常多样的表现形式和性质。其中，局部形式包括原函数(如共轭一致性)与微分等式；而全局形式包括积分等式、不变量和不变式。局部形式比较适合于部分数据补全等，而全局形式比较适合于全局参数估计或伪影校正等。这些不同的表现形式，能在一定程度上影响数据一致性条件的利用难度，以及对特定CT应用的适应性。本文重点综述CT数据一致性条件形式和性质及其在CT成像中的应用。

1 映射算子及成像几何

CT理论中的各种映射算子[如Radon变换、X-ray变换、发散束(扇束、锥束)变换等]将物体函数映射为非物体函数。由于映射算子固有性质显示出了一些独立于物体函数的独特性质(例如，对于二维平行束正弦图中，每个投影的积分都是常数)，将这些特性统称为数据一致性条件[22]。本文映射算子所涉及的CT成像投影几何如图3所示。

图3 各种CT成像投影几何(a)圆形轨迹平行束；(b)圆形轨迹等角扇束；(c)圆形轨迹等距扇束；(d)圆形轨迹等角锥束；(e)圆形轨迹等距锥束

2 数据一致性条件及其应用

2.1 共轭一致性条件

共轭一致性条件(Conjugate Consistency Condition，CCC)[23～26]一般应用于二维投影几何中，也可以近似推广到三维投影几何。

2.1.1 共轭一致性条件

在二维投影几何中，共轭一致性条件特指[23-26]：

<圆形轨迹平行束>

p2(s,θ)=p2(-s,θ+π)

(1)

<圆形轨迹等角扇束>

(2)

<圆形轨迹等距扇束>

(3)

式中，θ为圆形轨迹平行束投影角度；β为圆形轨迹扇束投影角度；γ为圆形轨迹等角扇束扇角；s为圆形轨迹平行束的探测器像素在探测器坐标系上的空间位置；u为圆形轨迹等距扇束的探测器像素在探测器坐标系上的空间位置；D为源点到探测器中心点距离。

2.1.2 特点

共轭一致性条件的物理意义：颠倒任意一条投影路径两端的X射线源点与探测器像素点位置，理想情况下所得到投影数据严格相等。

共轭一致性条件的特点：① 原理简单易掌握；② 在投影域具有局部性；③ 投影原函数形式，不需要积分或微分；④ 可方便地从二维扩展到三维。

2.1.3 应用

Tang等基于二维共轭一致性条件，构造并证明“共轭投影误差加权和等于零”，并可将其应用于运动校正[23]。2005年与2006年，Tang等将三维共轭一致性条件分别用于圆形锥束与螺旋锥束CT重建算法设计中，通过三维加权方案来有效实现锥束伪影校正[24-25]。2018年，Li等尝试将三维加权方案应用到锥束CT重建迭代算法设计中，取得了一定效果[26]。

图4 基于共轭一致性条件的锥束伪影校正[24](a)校正前图像；(b) 校正后图像(经原作者同意)

2.2 微分限制条件

微分限制条件(Differential Constraint Condition，DCC)[24]应用于二维平行束投影几何中。

2.2.1 微分限制条件

在二维平行束投影几何中，微分限制条件特指[27]：

<圆形轨迹平行束>

(4)

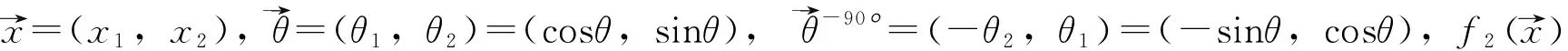
2.2.2 特点

2.2.3 应用

2011年Tang等基于二维平行束微分关系[31]：

<平行束>

(5)

得到了微分限制条件[式(4)]，并基于两步Hilbert变换[28]将其应用于二维梯度图像重建[27]。

图5 基于两步Hilbert变换与微分限制条件的二维梯度图像重建[27](a)(b)无截断；(c)(d)有截断(经原作者同意)

2.3 Helgason-Ludwig一致性条件

Helgason-Ludwig一致性条件(Helgason-Ludwig Consistency Condition，HLCC)[29-31]应用于二维平行束投影几何中。

2.3.1 Helgason-Ludwig一致性条件

在二维平行束投影几何中，Helgason-Ludwig一致性条件特指[31]：

<圆形轨迹平行束>

(6)

式中，左侧为二维平行束投影矩，右侧为二维图像矩作为系数的cosθ与sinθ的m阶多项式。

2.3.2 特点

Helgason-Ludwig一致性条件的物理意义：反映了二维平行束投影矩与二维图像矩之间的等式关系。

Helgason-Ludwig一致性条件的特点：① 投影矩为cosθ与sinθ的m阶多项式；② 在投影域具有全局性；③ 投影积分形式；④ 速降函数空间的充要条件。

2.3.3 应用

2000年，Basu等基于Helgason-Ludwig一致性条件构造并证明了一个确定投影数据的所对应变量(s,θ)的条件[32]，该方法可用于MRI与三维电镜动态成像。Helgason-Ludwig一致性条件还可用于CT投影数据截断补全或FOV扩大[33-36]，任一角度投影数据估计[37-38]，投影数据任意损失补全[39]，以及基于运动估计的动态成像[40-43]、射束硬化伪影校正[44-47]、散射校正[48]。

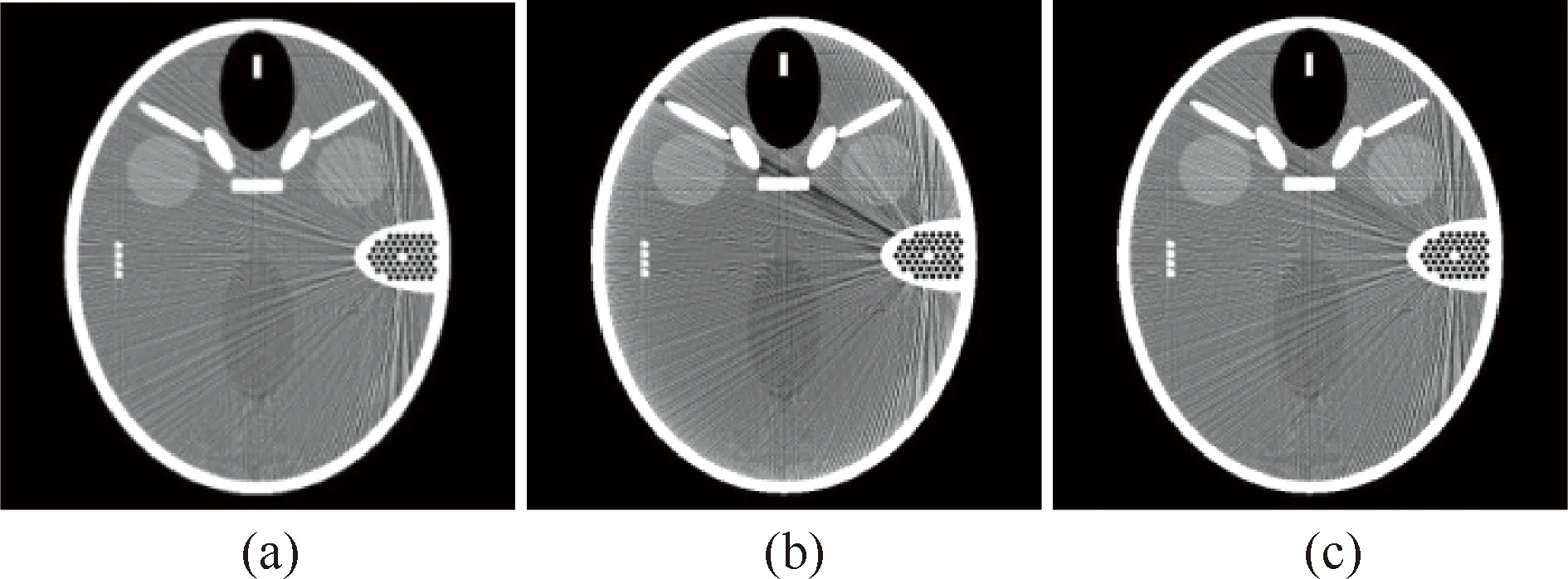
图6 基于Helgason-Ludwig一致性条件的射束硬化伪影校正[47](a)单能谱重建图像；(b)宽能谱重建图像；(c)校正后图像(经原作者同意)

2.4 扇束数据一致性条件

扇束数据一致性条件(Fan-beam Data Consistency Condition，FDCC)[47]应用于二维扇束投影几何中。

2.4.1 扇束数据一致性条件

在二维等角扇束投影几何中，2005年，Chen等证明的扇束数据一致性条件特指[49]：

<圆形轨迹等角扇束>

(7)

该式本质上是投影域一维有限Hilbert逆变换[50-51]，其中

(8)

(9)

β′=π+β+γ+sin-1(p′/R)

(10)

(11)

2.4.2 特点

扇束数据一致性条件的物理意义：投影数据可由共轭侧投影数据的一维有限Hilbert逆变换得到。

扇束数据一致性条件的特点：① 比共轭一致性条件更复杂，可看作不同的插值方法；② 投影积分形式；③ 存在奇异积分。

2.4.3 应用

扇束数据一致性条件可用于缺失数据修补恢复[49]，也可用于运动伪影校正[52]。

2.5 扇束数据充要条件

扇束数据充要条件[53]应用于直线轨迹二维扇束投影几何中。

2.5.1 扇束数据充要条件

在二维等角扇束投影几何中，2013年Clackdoyle证明的扇束数据充要条件特指[53]：

<直线轨迹等角扇束>

(12)

式中，τ对应于源点在直线轨迹上的位置。该充要条件也有等距扇束形式，此处不再赘述。

2.5.2 特点

扇束数据充要条件的特点：① 投影积分形式；② 不存在奇异积分；③ 相比通过变量代换推导的扇束投影数据Helgason-Ludwig一致性条件，扇束数据充要条件形式上更类似于平行束Helgason-Ludwig一致性条件，因此使用将更方便。

2.5.3 应用

扇束数据充要条件可能应用于丢失数据补全。

2.6 截断数据一致性条件

截断数据一致性条件(Truncated Data Consistency Condition)[54-55]可应用于一般轨迹二维平行束或扇束投影几何中。

2.6.1 截断数据一致性条件

在二维平行束或扇束投影几何中，2015年Clackdoyle等证明的圆形轨迹截断数据一致性条件特指[54]：

<圆形轨迹等角扇束>

(13)

(14)

(15)

(16)

2.6.2 特点

截断数据一致性条件的物理意义：Bn(x1)为x1的n阶多项式，直线轨迹扇束数据一致性条件在圆形轨迹上的应用。

截断数据一致性条件的特点：① 适用于特定截断数据情形；② 投影积分形式；③ 避免了奇异积分。

2.6.3 应用

截断数据一致性条件可用于运动伪影校正[54-55]。

2.7 积分不变量

积分不变量(Integral Invariants)[56]可应用于发散束(扇束、锥束)投影几何中。

2.7.1 积分不变量

在发散束几何中，2006年Wei证明了大量的积分不变量[56]，因为篇幅原因仅列举如下直线轨迹等角扇束与等角锥束各一例：

<直线轨迹等角扇束>

(17)

式中，τ对应于源点在垂直坐标轴上的位置；b为任意实数，但要求投影不发生截断。

<直线轨迹等角锥束>

(18)

2.7.2 特点

积分不变量的物理意义：I2与IIV分别为源点在垂直坐标轴上的位置τ不变量。

积分不变量的特点：① 与运动对称群理论相关；② 投影积分形式；③ 特定形式的积分不变量需奇异积分。

图7 积分不变量的奇异性[58](a)非奇异情形;(b)奇异积分情形(经原作者同意)

2.7.3 应用

积分不变量可用于运动伪影校正[56]，成像系统几何校正[57]，也可用于稀疏角度投影的射束硬化校正[58]。根据运动的相对性，当源点不动物体沿着垂直方向运动时，I2与IIV积分不变量无法感知到物体运动。因此，对运动伪影进行校正时，需要清晰理解所采用的积分不变量对不同运动的感知能力。

图8 基于积分不变量的射束硬化伪影校正[58](a)校正前图像；(b)校正后图像注：稀疏角度投影数为64，采用环形模式不导致奇异积分(经原作者同意)

2.8 锥束数据一致性条件

锥束数据一致性条件[59]顾名思义可应用于锥束投影几何中。

2.8.1 锥束数据一致性条件

在三维锥束投影几何中，2016年Clackdoyle等[59]证明了一族锥束数据一致性条件：

<圆形轨迹等距锥束>

(19)

(20)

(21)

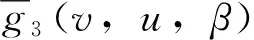
2.8.2 特点

锥束数据一致性条件的物理意义：Mn(β)为cosβ与sinβ的n阶多项式[59]。

锥束数据一致性条件的特点：① 投影积分形式；② 存在奇异积分；③ 相比通过变量代换推导的扇束投影数据Helgason-Ludwig一致性条件，锥束数据一致性条件形式上更类似于平行束Helgason-Ludwig一致性条件，因此使用将更方便。

2.8.3 应用

锥束数据一致性条件可应用于丢失数据补全，也可用于投影非线性或全局伪影等整体缺陷因素的校正，例如，射束硬化和散射校正或全局运动参数估计等。

2.9 约翰方程

约翰方程(John’s Equations)[60]可应用于三维锥束投影几何中。

2.9.1 约翰方程

在三维锥束投影几何中，1938年John[60]证明了一组有四个独立变量的超双曲方程：

<三维锥束>

i,j=1,2,3

(22)

2.9.2 特点

约翰方程的物理意义：三维锥束投影必须满足四个独立变量的超双曲方程组。

约翰方程的特点：① 投影微分形式；② 可用傅里叶变换也可用PDE进行数值计算；③ 推导到不同投影几何与扫描轨迹较困难易发生错误。

2.9.3 应用

约翰方程可应用于三维PET投影数据重排[61]、基于三维傅里叶变换的锥束投影数据补全[62]、基于PDE的投影数据补全[63]、心脏运动伪影校正[64]、螺旋锥束CT投影数据重排[65]、变螺距锥束CT重建[66]、散射校正[67-68]。另外，2005年Sidky等针对X射线源点位于二维圆柱面上的三鞍线情形，提出一个不同的锥束投影数据一致性条件[69]。与约翰方程稍有不同，并猜想可用于缺失锥束投影数据补全，并推断如猜想成立，则三鞍线X射线源轨迹下整个三维ROI中的图像函数可重建。

图9 基于约翰方程的散射校正[67](即PC-VI算法)的原理性示意图(经原作者同意)

图10 基于约翰方程的散射校正[68]其中Uncorrected为未校正结果，SI为空域插值结果，PC-VI为[67]结果，JECC为[68]结果(经原作者同意)

2.10 频域双楔形零能量区域性质

频域双楔形零能量性质[22]可应用于平行束、扇束投影几何中。

2.10.1 频域双楔形零能量性质

2010年Mazin等将二维平行束投影几何的频域双楔形零能量性质推广到二维扇束投影几何，该性质作为二维投影数据必须满足的必要条件也可看作一种独特的数据一致性条件[22]。

2.10.2 特点

频域双楔形零能量性质的物理意义：ROI内的图像函数能量落在频域双楔形零能量区域外，ROI外的图像函数能量落在全频域。

频域双楔形零能量性质的特点：① 在频域工作可利用FFT高效率性质；② 可用于数据压缩；③ 可用于投影噪声能量估计。

2.10.3 应用

2010年Mazin等将频域双楔形零能量性质应用于提高迭代重建算法效率的工作中[22]。2013年Bai等将频域双楔形零能量性质应用于投影噪声能量估计，并将其用于统计迭代重建的正则化参数选择[70]。

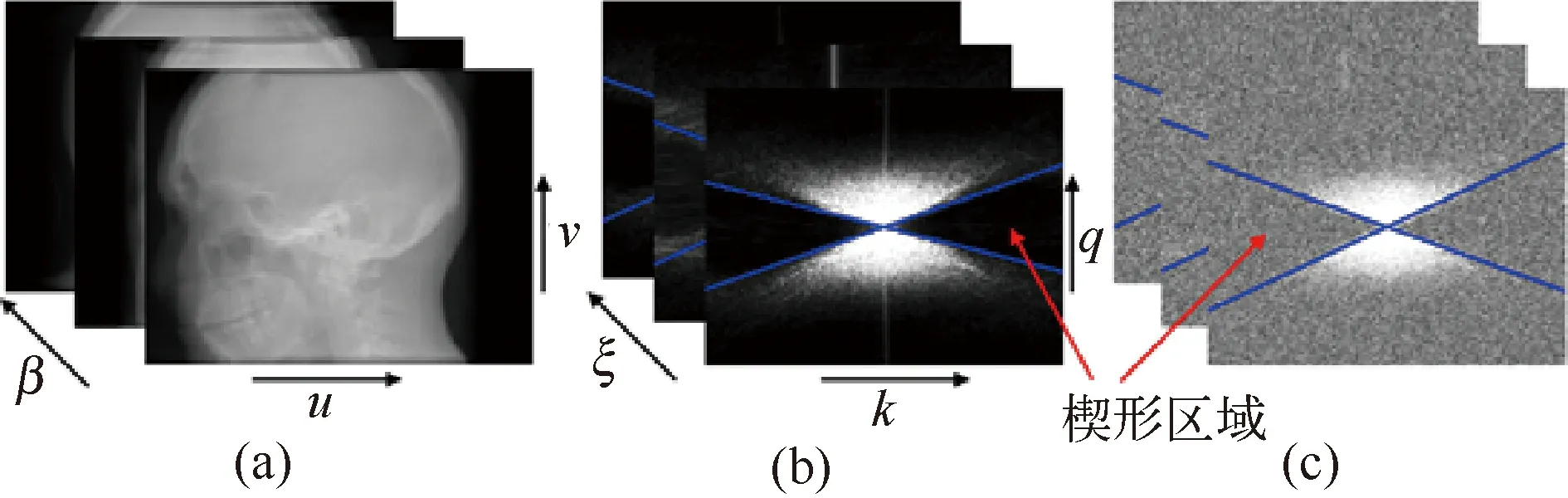
图11 基于频域双楔形零能量性质的投影噪声能量估计[70](a)锥束投影数据；(b)无噪数据傅里叶空间；(c)含噪数据傅里叶空间(经原作者同意)

3 讨论

数据一致性条件有着非常多样的表现形式，如：

(1)平行束扇束锥束投影几何；

(2)直线圆形螺旋一般扫描轨迹；

(3)局部全局运算形式；

(4)原函数微分积分运算形式；

(5)积分运算为奇异非奇异；

(6)不变量多项式频域特定性质。

局部形式包括原函数(如共轭一致性)与微分运算形式；而全局形式包括积分运算形式。局部形式允许投影域截断，而全局形式不允许投影域截断。非奇异形式一般数值计算稳定，而奇异形式一般数值计算不稳定。这些不同的表现形式，能在一定程度上影响数据一致性条件的利用难度，以及对特定CT应用的适应性。

在Gowers主编的《普林斯顿数学指南(第一卷)》[71]的I.4数学研究的一般目的(第82页)这篇文章中，作者对“不变式”的性质进行了很好的论述：对于一个不变式，时常寻求它的两种主要性质，而这两种性质又时常是向两个相反方向起作用的。其一是要它尽可能的细，意思是只要两个对象不等价，不变式就不同。其二是要能够实际确定何时不变式不同。一个不变式哪怕是很细，如果无法算出来，那就没有多大用处。所以，最强有力的不变式大概是哪些既能够计算出来，又不太容易计算出来的不变式。然而，有时证明对象不等价是很困难的，以至于不变式尽管能部分时间有用，也认为是有用而且有趣的。以上论述也完全适用于本文讨论的数据一致性条件，因此，应用时也理应同样谨慎。

CT成像过程中由于被成像物体、系统几何或扫描过程缺陷[22]，会导致CT重建图像中表现出伪影[13,15]，进而影响CT图像质量与后续诊断，因此，需要进行相应伪影校正。CT图像伪影多种多样，如部分体积伪影、射束硬化伪影[44-47,58]、运动伪影[23,40-43,52,54-56,64]、采样伪影[37-39,62-63,69]、电子伪影、探测器余晖伪影、金属伪影[45-46]、截断伪影[33-36,49,70]、散射伪影[48,67-68]、风车伪影[14-18]、锥束伪影[24-26]、阶梯伪影等。有必要对CT成像伪影产生机制开展深入研究，评估各种数据一致性条件对伪影校正的适应性。数据一致性条件也被用来改进重建算法的计算效率[22,61,65-66]。基于数据一致性条件的方法可广泛应用于CT、PET、SPECT和MRI等多种成像模态。

另外，2012年Tang等对发散束CT各种数据一致性条件之间的逻辑关系采用易被科研人员理解的数学语言进行了梳理[72]，结合本文，相信对从事相关研究工作的科研人员会有一定帮助。2011年Wei 等对发散束投影与Radon变换之间提出了一系列的关系[73]，可涵盖以前相当多的研究成果。都有着很好的参考价值。

4 结论

本文综述了各种CT数据一致性条件，及其不同表现形式与应用场合。对数据一致性条件的综合研究有助于从不同侧面理解现代CT成像理论的内涵。基于数据一致性条件设计新伪影校正或图像重建方法并评估其应用性能，将成为现代CT成像理论与应用研究的重要组成部分，值得业界对其进一步开展深入研究。