导数中的不等式证明策略研究

吴艳丽

(黑龙江省大庆市第二中学)

导数中不等式的证明问题,历来出现在高考命题的压轴题中,由于不等式证明方法灵活性很强,因此这类问题具有很高的研究价值.基于此,本文结合具体问题,阐述几种常见的解题方法,以期抛砖引玉.

1 构造函数法

将不等式的证明问题转化为函数单调性的应用问题进行求解,这是这类问题最常用的方法,这种方法体现了函数、方程、不等式三者之间的内在联系.运用这种方法一般分为三个步骤:1)合理构造函数;2)利用导数证明函数的单调性;3)利用函数的单调性证明不等式.

例1若函数f(x)＝1－,点A(1,1)是曲线y＝f(x)与y＝g(x)的公共点,且它们在点A处的两条切线互相垂直.

(1)求a,b的值;

(2)证明:当x≥1时,f(x)＋g(x)≥

(1)a＝b＝－1(具体求解过程略).

当需要证明的不等式两边都含有同一个变量时,我们通常可以直接构造“左减右”的函数,再应用它的导函数来探究它的单调性.

2 放缩法

当所证不等式的不等号中不含等号时,可考虑用放缩法证明,在证明过程中将某部分函数式用另一个函数值比较大(或者比较小)的函数替换,从而构造新的函数,再利用函数的单调性加以证明.

例2已知函数f(x)＝

(1)求函数f(x)的单调区间;

(2)证明:当x＞0时,都有

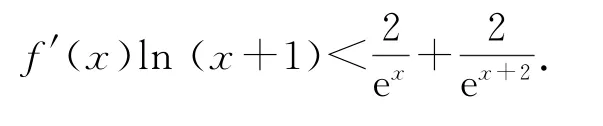
(1)函数f(x)在(0,1)上单调递增,在(1,＋∞)上单调递减(求解过程略).

易证lnx≤x－1,当且仅当x＝1时等号成立(证明过程略),所以0＜ln(x＋1)＜x(x＞0).

综上,当x＞0时,f′(x)ln(x＋1)＜

含有lnx或ex的函数是超越函数,在解决具体问题时应根据这两类函数的特点及结构特征,对不等式实施灵活变形,并注意重要不等式lnx≤x－1⇔ex≥x＋1的合理代换.

3 切线法

所谓切线法,就是证明某曲线的图像恒位于某一点切线处的上方或下方,本质上看就是利用导数研究函数图像的分布,这种方法体现了数形结合思想.

例3已知函数f(x)＝ex－x2.

(1)求曲线f(x)在x＝1处的切线方程;

(1)曲线f(x)在x＝1处的切线方程为y＝(e－2)x＋1(具体求解过程略).

(2)令g(x)＝f′(x),则g′(x)＝ex－2,当x＜ln2时,g′(x)＜0,当x＞ln2时,g′(x)＞0,故函数f′(x)在(－∞,ln2)上单调递减,在(ln2,＋∞)上单调递增.又gmin(x)＝g(ln2)＝f′(ln2)＝2－2ln2＞0,故函数f(x)在(0,＋∞)上单调递增.由(1)知曲线f(x)在x＝1处的切线是y＝(e－2)x＋1.

又f(1)＝e－1,于是可以猜想函数f(x)的图像位于切线y＝(e－2)x＋1的上方.

我们先来证明当x＞0时,f(x)≥(e－2)x＋1.

设h(x)＝f(x)－(e－2)x－1(x＞0),则

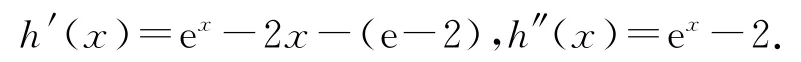
当0＜x＜ln2时,h″(x)＜0,当x＞ln2时,h″(x)＞0,故h′(x)在(0,ln2)上单调递减,在(ln2,＋∞)上单调递增.由h′(0)＝3－e＞0,h′(1)＝0,0＜ln2＜1,则h′(ln2)＜0,故存在x0∈(0,ln2),使得h′(x0)＝0,故当x∈(0,x0)∪(1,＋∞)时,h′(x)＞0,当x∈(x0,1)时,h′(x)＜0,故h(x)在(0,x0)和(1,＋∞)上单调递增,在(x0,1)上单调递减.

又因为h(0)＝h(1)＝0,故h(x)≥0,即f(x)≥(e－2)x＋1,当且仅当x＝1时等号成立,故当x＞0时,ex－x2≥(e－2)x＋1,即≥x,又因为x≥lnx＋1,当且仅当x＝1时等号成立(证明过程略),所以≥lnx＋1,当且仅当x＝1时等号成立.

利用切线法证明这类不等式时,往往还要用到放缩法,这种方法灵活性强.当然这种方法的出现往往不是凭空产生的,当问题的第(1)问要求我们求曲线在某一点处的切线方程时,我们往往要考虑能否运用切线放缩法来证明不等式.

4 应用函数的凹凸性

在不等式恒成立问题中,有些试题往往以曲线与切线静态或者动态的位置关系为几何背景,这时我们可以着眼于曲线的凹凸性,从而获得清晰自然的思路.

例4已知函数f(x)＝(x＋1)lnx,曲线y＝f(x)在x＝1处的切线方程为y＝ax＋b.

(1)求证:x＞1时,f(x)＞ax＋b;

(1)当x＞1 时,f(x)＞2(x－1)(证明过程略).

(2)由(1)知当x＞1时,有(x＋1)lnx＞2(x－1).令x＝n2－2＞1(n≥2,n∈N*),则

本题中f(x)的一阶导函数为f′(x)＝lnx＋二阶导函数为f″(x)＝＞0,这说明原函数f(x)是凹函数,故不等式(x＋1)lnx＞2(x－1)恒成立.

导数中不等式的证明问题是一个永恒的话题,也是一个永远值得研究的课题,这类问题的解决没有相对固定的思路与方法,面对具体问题,我们必须从问题的实际情况出发制订解题方案.因此解答这类问题不可故步自封,不可按部就班,应大开脑洞,打破常规,不断探索,善于从数学的基本思想与方法的角度去分析问题,才有可能找到解决这类不等式证明问题的最佳思路与方法.

(完)