隧道爆破振动信号畸变校正与混沌多重分形特征研究

付晓强， 俞 缙， 刘纪峰， 杨仁树， 戴良玉

(1. 三明学院 建筑工程学院，福建 三明 365004；2. 华侨大学 福建省隧道与城市地下空间工程技术研究中心，福建 厦门 361021；3. 三明科飞产气新材料股份有限公司，福建 三明 365500； 4. 北京科技大学 土木与资源工程学院，北京 100083)

隧道钻爆法过程中，不可避免会对周围环境产生负面影响，爆破振动监测作为爆破损伤评估、孔网参数调整优化的重要依据，对指导工程施工具有积极的现实意义[1-2]。目前，隧道开挖仍普遍采用毫秒雷管进行振动控制，鉴于普通雷管起爆精度的不确定性和爆破振动控制的不稳定性，通过定性和直观分析无法准确对爆破效果进行科学评价，信号的深入分析成为必然趋势。由于测试环境复杂性和仪器本身的原因，监测信号中均不同程度含有干扰成分，如噪声、趋势项等，上述不相干分量在信号预处理过程中必须准确辨识并有效分离，才能消除其对信号真实信息的干扰，这也是现阶段信号处理的关键问题。如王海龙等[3]对隧道爆破信号中的噪声特征进行了分析，提出了适合隧道爆破信号去噪组合方法；贾贝等[4]针对经典模态分解方法的缺陷，采用变分模态分解方法对隧道爆破信号趋势项进行了消除，并对相关影响因素进行了分析；张胜等[5]通过构造自适应小波基有效去除了奇异信号中包含的趋势项，后续能量分析过程也验证了算法的精度；Liu等[6]采用小波阈值方法对不同装药结构爆破信号进行了分析，提取得到不同结构下的信号特征。上述算法在爆破信号处理方面均显现出独特的优势，但对于噪声和趋势项同步联合处理分析还未见广泛报道。

近年来，爆破信号非线性特征亦为研究分析的热点。非线性特征蕴含着反映爆破本质和破岩机理的重要信息，如时频域、能量熵、分形和混沌特性等，如Zhao等[7]采用时频分析方法分析了爆心距对信号频谱特征的影响，细化了爆心距对信号特征的关键作用；赵明生等[8]采用二次型平滑伪魏格纳-维尔分布算法对不同微差间隔下的单段叠加信号的振速峰值和主频特征进行分析，提出了将能量作为建(构)筑物损伤影响的量化参数；单仁亮等[9-10]采用小波包方法对隧道和立井模型试验监测信号进行了能量特征提取，总结得到了爆破能量衰减规律，为类似工程爆破安全评估提供依据；钟明寿等[11]基于多重分形理论对碳酸盐岩爆破地震波的分形行为进行了研究，精确描述了爆破信号的局部奇异性和分形特征；付晓强等[12]运用混沌理论揭示了冻结立井爆破信号不同频带子信号的混沌吸引子形态特征，研究结果表明混沌吸引子形态变化可作为信号主频判别和能量表征的指标。

本文依托青岛地铁3#线隧道掘进工程，对隧道掘进爆破振动进行了有效监测。采用稀疏化基线估计与去噪(baseline estimation and denoising with sparsity，BEADS)算法实现了信号趋势项、噪声和真实信号的分离，利用多重分形去趋势波动分析(multi-fractal detrended fluctuation analysis，MF-DFA)方法分析了信号不同分量的多重分形和混沌特征，并基于交叉小波变换对不同成分信号的时频相关性进行了分析，深刻揭示了爆破信号的非线性行为特征，为信号不同成分的有效辨识和特征分类提供了探索性思路。

1 基本算法

1.1 BEADS算法

将复杂信号分解为简单分量的线性组合是信号分析的重要途径。稀疏分解理论认为，信号分解结果越稀疏则越接近信号的本征或内在结构，信号稀疏表示可有效揭示非平稳信号的时频结构[13]。对于任意稀疏化信号s(t)，若其中含有N点随机成分，则该信号可表示为本征分量与缓变漂移信号的组合，即

s(t)=x(t)+f(t)，s(t)∈RN

(1)

式中：x(t)为包含无数峰值的稀疏可微本征信号成分；f(t)为信号中含有的缓变基线偏移成分，其为低通分量。受外界环境影响，测试信号中通常亦会含有一定的随机噪声。因此，可将受基线偏移和噪声影响的信号y(t)进一步表示为

y(t)=s(t)+w(t)=x(t)+f(t)+w(t)，y(t)∈RN

(2)

式中，w(t)为奇异信号中含有的随机干扰噪声。上述分量信号的有效分离依赖于相关参数的精确选取，如截止频率fc，其决定了基线分量与剩余分量信号之间的界限；不对称系数r，用于补偿运算过程中产生的频谱负值；正则化参数λ(λ0～λ2)，可控制分解信号x(t)的稀疏性。另外一个重要的参数为幅值A，其乘以正则化参数(A×λi)便可使得λi选取与信号幅值无关。

基线成分为信号中缓慢变化的趋势分量，为信号漂移、仪器漂零或测试环境引起的偏差，通过建立低通滤波器提取；白噪声为信号中包含的高频噪声，通过建立高通滤波器获取；将上述两个分量从初始信号中剔除，便得到了能够反映信号信息特征的真实信号。

1.2 MF-DFA算法

多重分形去趋势波动分析方法是在传统波动去趋势项分析(detrended fluctuation analysis，DFA)方法的基础上改进而提出的，其能够有效揭示爆破振动等这类非线性、非平稳信号的动力学行为[14-15]。相较与传统的多重分形算法，其核心优势主要有：①充分利用信号序列数据长度，正反双向对信号序列进行等时间长度划分；②通过最小二乘法对各个分段进行多项式拟合，消除数据序列中非平稳趋势的影响；③利用不同阶次波动函数分析时间序列在不同层次上的标度行为，精细刻画数据序列的分形特征，揭示隐藏在非平稳时间序列的多重分形特征。

对于长度为N的爆破振动信号时间序列{x(k),k=1,2,…,N}，MF-DFA求解过程如下。

计算{x(k)}偏离均值的累计离差y(i)

(3)

将y(i)划分为Ns个等长度s的小区间序列，即

Ns=int(N/s)

(4)

由于在划分过程中N未必恰好是s的整数倍，则必定会存在除不尽的余值。为了保证数据序列不丢失信息，将这部分余值保留并从y(i)尾部开始，逆向重复上述划分过程，便会得到2Ns个子序列。

利用最小二乘法拟合各个子序列的局部趋势函数yv(i)为

yv(i)=a0+a1i+a2i2+…+akik

(5)

式中：ai为拟合多项式的系数，i=0,1,…,k；k为多项式拟合最高阶数。

对于奇异爆破信号，“趋势项”的消除是通过离差y(i)减去拟合局部趋势函数yv(i)来实现的，因此不同拟合阶数i可体现“趋势项”被消除的程度。

(6)

确定q阶波动函数Fq(s)

(7)

式中，阶数q的取值为非零实数。特别地，当q取值为2时则退化为标准的DFA法。若序列{x(k)}存在自相似特征，则其具有多重分形特征。则q阶波动函数Fq(s)与s之间存在幂律关系[16]

Fq(s)～sh(q)

(8)

式中，h(q)为广义Hurst指数，表征原始序列的相关性，h(q)大小取决于q值的变化。当信号{x(k)}为单分形时间序列，则F2(s,v)在所有小区间标度是恒定值，此时h(q)为与q值无关的常数。

1.3 MF-DFA和经典多重分形理论关系

通过MF-DFA方法得到的h(q)和经典多重分形算法中由标准配分函数得到的标度指数τ(q)存在如下关系[17]

τ(q)=qh(q)-1

(9)

结合Legendre变换对式(9)等号两边对q求导便得到多重分形谱f(a)，奇异指数α和τ(q)三者之间满足关系

(10)

2 隧道爆破信号零偏校正

青岛地铁3#线隧道全长25.93 km，采用钻爆法施工。开挖断面为马蹄形，掘进断面积为30.8 m2，宽度为5.8 m，高度为6.1 m。隧道爆破选用共7个段别电雷管，分别为MS1～MS13跳段使用，可以最大程度降低爆破产生的振动效应。选用2#岩石乳化炸药，布置掏槽孔24个，分别采用MS1、MS3、MS5三段起爆，对应的各段别起爆药量为7.2 kg、7.2 kg和10.8 kg；辅助孔40个，分别为MS5、MS7、MS9三段起爆，各段别起爆药量分别为1.8 kg、10.2 kg和12 kg；周边眼30个，为MS11段起爆，起爆药量为13.5 kg；底眼7个，为MS13段起爆，起爆药量为4.2 kg。单循环总装药量为66.9 kg，具体炮眼布置如图1所示。

图1 爆破孔网参数(mm)

为了准确评估和反映隧道爆破产生的振动效应，在隧道开挖掌子面上方22 m处布置测点。测试采用TC-4850型爆破测振仪，测振仪参数的准确设定是保证爆破信号测试精度的前提条件。为了保证测试波形的完整性及满足Heisenberg测不准原理的要求，将采样频率设定为8 kHz，采样时长为2 s。测振仪具体测试分析流程如图2所示。

图2 TC-4850测试及分析流程

测试时建立笛卡尔坐标系，将测振传感器水平x向(径向)指向隧道掘进轴线方向，y向(切向)指向与轴线垂直的水平方向，z向(垂向)指向与xy所构成平面垂直的竖向,从而获取相互垂直的三个方向上的振动信息。测振仪监测到的典型畸变振速波形如图3所示。

图3 隧道爆破振动信号波形曲线

三向振速波形出现显著差异，其中与隧道轴线平行的x向振速最大，y向次之，z向最小。与常规露天爆破等多自由面爆破不同，隧道爆破掘进自由面单一，岩石夹制力较大，导致在装药量较小的低段别产生强振，伴随后续段别的顺利起爆，瞬间形成第二附加自由面，振速幅值有所降低；另一方面，雷管段别越高，雷管误差相对也越大，这也解释了该隧道微差起爆周边眼的MS11段总装药量大反而产生的振动却较小的原因。高段别雷管误差范围相对较大，再加上炮孔数量较多，一定程度上形成了独立的小型微差起爆网路，避免了周边眼各炮孔瞬时起爆产生的振速峰值“叠加效应”。从图3可知：隧道爆破振动主振波形持续时间主要位于0～1 s内，在0.8 s后逐渐衰减直至基线零点附近，符合爆破方案中雷管起爆及延期误差时程分布区间规定(MS13段雷管起爆时刻标定值为：650 mm，下限为600 mm，上限为705 mm)。同时应注意到，三向振速波形曲线均存在一定的基线偏移现象，尤其以z向最为显著，因此选取z向信号进行分析，其波形局部特征如图4所示。z向信号在振动起始端部产生明显的零漂，而在主振时程后具有明显的“甩尾”趋势项。引起这种现象的原因是多方面的，如仪器标定问题、爆破飞石、测试环境和测点布置等，若后续分析中将这类信号直接舍弃，会导致测试数据不完整，数据信息丢失甚至影响后期相关结论的科学性。因此，如何提高这类信号的可读性和辨识度，是目前技术人员面临的关键问题。

图4 隧道爆破振动信号(z向)

信号分析过程中往往需要输入多个相关参数，以确保得到的真实信号具有明确的物理意义。采用BEADS算法对信号进行处理时，所选截止频率的微小变化会引起基线成分的较大波动，尤其在低于最佳频率的中心频率处体现的更为明显，此外，高于最佳频率的截止频率会使基线成分对信号峰值极为敏感。考虑到基线成分主要集中在信号低频区域，故设定分析截止频率fc为0.002 Hz。

在分析过程中为了降低基线校正过程对信号分量幅值的影响，引入正则化系数λ和具有非对称补偿罚值功能的对称损失函数φ。为了从y中提取x，问题转化为下述优化问题，也称为基追踪去噪(basic pursuit denoising，BPD)过程

(11)

(12)

式中：φ:R→R为罚函数；参数λ决定了该过程中信号稀疏化程度。由于基线成分主要位于信号低频分量中，分析时设置滤波器阶数d取为0～2，损失函数非对称性系数r取为6。正则化参数基本幅值λ为0.8，不同阶正则化参数λ0～λ2分别为：0.8、3.2和4.0。分析过程中干扰因素很大程度上可通过调整非对称系数r和正则化参数λ实现，信号分解提取结果及对应的信号频谱，如图5、图6所示。BEADS算法通过建立凸优化问题来封装上述分析过程中的非参数模型，引入类似正则化1范数的非对称损失函数，是一种具有鲁棒性、高效性且能快速收敛至最优唯一解的迭代算法。图7中损失函数值与迭代次数历史关系曲线表明，经过有限次数(<15次)的迭代损失函数值便趋于收敛，验证了算法运行效率。

图5 信号BEADS分析结果

图6 信号不同成分功率谱密度

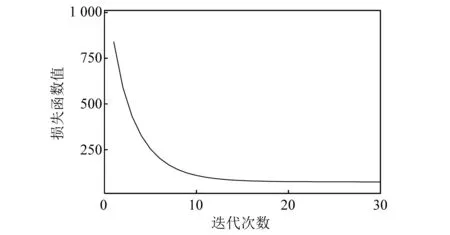
图7 损失函数迭代历时曲线

3 混沌多重分形特征分析

3.1 混沌特征

隧道微差起爆网路可视为复杂的非线性动力系统，爆破信号的非线性动力学特征具有对网路装药量、雷管段别选取等初始条件的敏感依赖性、起爆过程延期时间的不确定性以及能量时空分布的随机性。信号混沌运动轨迹称为混沌吸引子，混沌吸引子上的混沌行为是一种高级有序行为。为了便于观察不同分量信号相空间轨迹演化规律，将信号根据时间分成若干段，重构后投影到三维相空间中，绘制其吸引子演化过程，具体过程详见付晓强等[18-19]的研究。不同分量信号吸引子形态在三维相空间轨道的精细程度、相空间轨迹的收敛程度、信号不同成分所蕴含的信息量以及稳定程度具有显著差异，如图8所示。校正信号波形稳定规则，吸引子在相空间轨迹为长轴、短轴不等长的椭圆形平衡态，其在轨道之间表现为由密到疏的反复周期性波动过程，体现了微差爆破过程中低段别起爆能量的不断耗散和高段别起爆能量的相继补充作用；低频趋势项成分能量较小，吸引子在三维相空间收敛为近似直线，揭示了趋势项为大波动的长周期干扰特征；高频噪声振幅明显减小，吸引子在相空间周期性成分减弱，呈现为无明显轨道的杂乱无章状态，说明了噪声成分具有微幅随机性波动特征。

图8 爆破信号不同成分混沌吸引子形态演化

针对非线性信号特征的分析，Eckmann等提出了一种图形化的信号提取方法，即递归图(recurrence plot，RP)理论。递归图是一种能够深刻揭示信号不平稳并识别标量时间序列中隐含规律的图形方法，其从宏观角度分为均匀模式、周期模式、漂移模式和突变模式[20-21]。这里，分别计算三个分量信号的递归图，如图9所示。图9中不同分量信号递归图模式特征明显不同，递归拓扑结构清晰可辨。校正信号的递归图在时间轴上表现为周期模式，属于典型的稳态分布，局部密度增大与信号波峰、波谷出现位置密切相关，具有强烈的非线性特征；低频趋势项成分的递归图呈对角线方向分布，分布走向大致平行于45°主对角线方向，表现为突变模式且对角线和孤立点并存，说明趋势项属于信号中的缓慢变化成分，其线性程度增强；而噪声成分递归孤立点随机分布，表现为漂移模式，表明高频低幅噪声引起的干扰由信号中突然的或急剧变化所决定。递归模式和混沌特征为爆破信号不同成分的辨识提供了理论依据和参考。

图9 爆破信号不同成分递归图演化

3.2 多重分形特征

应用MF-DFA对图5中隧道爆破信号不同分量进行分析，将尺度s区间取为16～1 024并等间隔划分，共得到19个尺度值范围内的信号波动特性。计算时k值确定为2，取阶数q分别为-1,0,1，便得到校正信号、趋势项和噪声三个特征信号的双对数回归曲线，如图10所示。

图10 尺度函数波动双对数回归曲线

图10信号不同成分波动函数与尺度双对数拟合关系中，波动函数F(q)均随着尺度s的的变大而增大，F(q)对尺度s的对数回归线的斜率即为Hurst指数。图10中不同信号在尺度s变化下的波动趋于一致，随着尺度s的增加，波动聚集性增强，F(q)值差异性降低。校正信号的波动趋势更为明显，体现了不同段别雷管起爆能量对信号总能量的补充过程，其频率成分相对复杂，具有典型的瞬态非线性大波动特征；趋势项信号呈现近似线性的波动状态，体现了趋势项的小波动形态；噪声信号在大、小不同尺度s下的波动性态无明显差异，反映了噪声信号弱波动行为。

Hurst指数h(q)反映了信号不同阶数q之间的关系，是衡量信号多重分形特性的重要指标。计算爆破信号三种成分在不同阶数q下的Hurst指数值，如表1所示。从表1可知，爆破信号中不同成分的Hurst指数均随着q值增大而减小，体现了不同信号成分分形特征差异。

表1 爆破信号不同分量的Hurst指数

校正信号、趋势项和噪声在不同阶数下的Hurst指数呈现渐进式递减变化。通常Hurst指数取值介于[0,1]，h(q)值的变化可体现爆破信号的持续相关性。从表1可知：噪声成分00条件下为反持续相关性。三类信号Hurst指数变化具有清晰的辨识度，可作为信号辨识和分类的依据。

三种信号成分的多重分形谱及相关参数变化，如图11所示。图11(a)校正信号在幅值上介于低频趋势项和高频噪声之间，体现了校正信号宽频分布特征。图11(b)三者中趋势项的非线性特征最强，噪声最弱，校正信号居中，反映了校正信号多幅值属性。图11(c)表现出校正信号和趋势项分形谱对阶数q变化较为敏感，噪声却相反，这与表1得到的结论一致。图11(d)校正信号、趋势项及噪声信号标度指数τq与q均为非线性关系且校正信号非线性程度介于低频趋势项和高频噪声之间，在阶数q=0时三者标度指数值接近并趋于一致。阶数为负值时，标度指数能敏感地捕捉信号不同成分小幅值变化，反之，则能敏感反映其大幅值变化。可以看出无论哪类信号成分，q=0时，τq=-1，τq是一个凸向纵轴的函数，τq与q之间存在非线性关系且随着信号频率的增大非线性程度降低。

图11 爆破信号不同成分MF-DFA分析结果

图11(e)中奇异谱f(α)是奇异指数α的分维分布函数。多重分形谱f(α)有三个特征点，即左、右端点和极值点。多重分形奇异谱曲线在左端点的斜率q→+∞，因此左端点的横坐标α+∞对应着最大波动的奇异指数；在右端点处斜率q→-∞，因此，右端点的横坐标α-∞对应着最小波动的奇异指数。多重分形谱的宽度Δα=α-∞-α+∞反映了时间序列在整个分形结构上概率测度分布的不均匀性程度，Δα越大则概率测度分布越不均匀，多重分形越强烈。三种信号成分的多重分形谱及相关参数提取结果，如表2所示。

表2 信号MF-DFA分形谱参数

三类信号的奇异谱具有不同的形状、位置和谱宽，均为类似“钟形”曲线，表现为单峰拱形且峰值均为1，这是多重分形谱的一个重要特征。三种信号多重分形谱都是以α值的某个范围为特征，分形谱对应的奇异指数α随着信号频率的增大而逐渐左移；校正信号和趋势项Δf均为正值，噪声信号为负值。爆破信号不同成分奇异谱沿峰值点近似轴对称分布且校正信号的多重分形强度最大，趋势项次之，噪声信号最小。正是由于三类信号内在动力学机制不同，产生了上述谱差异。

4 信号相关性分析

对于任意给定的两个信号x(t)和y(t)，在其连续小波变换的基础上建立两者之间的相关性关系[22]

(13)

上述系数值变化可揭示信号在时频域不同尺度上的相关程度，其值越大则相关性越高，反之亦然。小波相关性凝聚谱综合反映了不同信号之间的相关性在时域和频域上的依赖关系，揭示不同信号成分与原始信号在时间和频率尺度上的相关程度。分析过程中，选用Morlet小波基函数可获得良好的时频域局部化特征，这里为了便于分析，对相关性进行归一化处理，如图12中颜色柱所示。图12中黑色小箭头代表被分析信号间的位相关系，箭头向右(→)表示两信号之间为同位相，为显著正相关；箭头向左(←)表示两者之间为反相位，呈现显著负相关关系；箭头垂直向上或向下(↑或↓)表示位相出现滞后性，为非线性相关。由相关性对比可知：校正信号与原始信号在全时程和特征频段(16～128 Hz)内表现出强烈的同位相相关性。基线信号与原始信号仅在主振时程0.7 s内存在一定的反位相趋势，且相关性出现间断不连续特征。噪声信号与原始信号在时频域上的依赖性显著降低，几乎无关联性。分析实践也表明如果截止频率选取合理，从原始奇异信号中将校正信号和基线信号成分去除得到的残余噪声理论上其与原始奇异信号无相关性。交叉小波凝聚谱清晰刻画了信号不同分量对原始信号特征的继承性，为三类信号的辨识提供了客观依据。

图12 不同信号成分与原始信号相关性凝聚谱

5 结 论

针对隧道爆破振动信号趋势项和噪声干扰识别难题，采用组合算法分离并提取信号的混沌分形特征，结论如下：

(1) BEADS算法可实现爆破校正信号、低频趋势项和高频噪声的有效分离，三者均具有多重分形特征且噪声具有绝对的反持续相关性，体现了其成分的波动离散性；趋势项具有持续相关性，持续性强弱与阶数q值大小为负相关，阶数q值越小，持续性特征越显著；校正信号以阶数q=0为转折点，在q<0条件下表现为持续相关性，而在q>0条件下为反持续相关性。

(2) 高频噪声、低频趋势项和校正信号三者的混沌特征显著不同。校正信号吸引子轨迹形态为反复周期性有序波动，其递归图具有周期模式；趋势项吸引子表现为近似直线，其递归图具有对角线分布突变模式；噪声吸引子为杂乱无章随机波动，其递归图具有漂移模式。

(3) 交叉小波变换凝聚谱可揭示信号在时域和频域变化的细部特征和共振位相差异，反映信号不同成分在时频域特征的相关程度，校正信号、趋势项和噪声分量与原始信号分别具有持续正相关、局部负相关和无相关性特征，为三类信号的分类识别和特征信息继承度判定提供了有效手段。