三参数Pasternak黏弹性地基中锥形桩的横向自由振动特性研究
张金轮, 张阿祥, 葛仁余, 孙俊伟
(安徽工程大学 建筑工程学院, 安徽 芜湖 241000)
锥形桩的楔型构造改变了桩周土的天然结构状态,可改善土的物理力学性质,有利于提高其承载力[1],适用于一般土层结构[2],具有显著的技术经济效果。我国于20世纪70年代已将圆锥形桩、正方锥形桩及矩形楔形桩等渐变截面桩应用于实践[3],由于对其承载特性及桩身侧面与桩周土相互作用的机理研究还不够充分,使得在设计使用时尚无对应的规范和计算方法,因而限制了其推广应用[4]。随着理论方法与试验技术的进步,相关变截面桩的动力特性研究逐渐受到关注[5-6]。单桩自振频率是其动力分析的基本参数,与地基的物理力学指标、桩的几何力学性质、质量分布情况及桩端约束条件等因素有关[7]。关于单桩自由振动特性的相关理论与数值研究,Yesilce[8]仅考虑地基弹性刚度的影响,利用微分变换法和微分求积元法对弹性地基上半刚体连接的Reddy-Bickford型矩形梁的横向自由振动特性进行分析。王奎华等[9]基于广义Voigt模型,在考虑桩身阻尼情况下,应用阻抗传递法及Laplace变换技术研究了成层土体中带明置承台单桩的纵向自由振动问题,给出了自由振动位移的半解析解,但并没有对桩的自振频率及其衰减系数进行具体分析。彭丽等[10-11]应用复模态方法研究了三参数黏弹性地基上等截面梁的横向自由振动特性,该法需求解超越方程使计算变得复杂。Mohammadimehr等[12]利用微分求积方法研究了三参数Pasternak黏弹性地基上锥形黏弹性微杆的横向自由振动特性。Ma等[13]对桩的临界荷载和屈曲结构进行解析求解,讨论了地基弹性刚度与剪切刚度对单桩的屈曲响应和自由振动特性的影响,但并未考虑地基阻尼的作用。柳伟等[14-15]基于Timoshenko梁理论的Winkler地基模型,运用回传射线矩阵法及求根法研究了黏弹性地基中单桩的外露长度、埋置深度、桩端约束情况对其纵-横向耦合自由振动各阶自振频率及其衰减系数与振型的影响,但未考虑地基剪切刚度的作用。Zhang等[16]基于Timoshenko梁理论,应用插值矩阵法研究了三参数Pasternak黏弹性地基上锥形梁的横向自由振动特性,将地基参数设为常量分析了两端简支边界下锥度系数与地基阻尼对梁固有频率的耦合效应。基于Euler-Bernoulli理论,Lee等[17]考虑长圆锥形摩擦桩的桩侧均布摩阻力与桩周土地基弹性刚度沿桩身的变化,建立了一种求解非均质弹性地基中锥形桩的固有频率和振型的理论模型;Liu等[18]同时考虑桩周土的线性轴向摩擦和线性侧移刚度,通过近似解析方法研究了非均质弹性地基中圆锥形摩擦桩的屈曲特性;但均未考虑桩周土阻尼与剪切刚度的影响。综上所述,目前考虑黏弹性地基中锥形桩有阻尼横向自由振动特性的研究鲜见报道。
本文在Zhang等研究的基础上,将桩体简化为线弹性锥形Timoshenko梁-柱,考虑圆截面锥形桩桩径沿纵向线性变化引起桩侧摩阻力与桩周土地基参数沿桩身纵向连续分布的不均匀性,提出三参数Pasternak黏弹性地基中锥形桩的动力学模型,利用微元体的平衡条件建立其振动控制方程,应用微分求积法与QR法求解该桩-土体系的横向自由振动响应。通过算例,分析了相应边界条件欠阻尼状态下桩身锥角、地基阻尼、地基横向弹性刚度与剪切刚度、桩侧摩阻力、轴向荷载、桩长径比等参数对其横向自由振动频率特性的影响。
1 锥形桩-土体系动力学模型及控制方程
1.1 基本假定及计算模型
结合现有研究成果,为便于建立方程,做以下基本假定:①将锥形桩简化为线弹性锥形Timoshenko梁-柱,即同时考虑桩横截面弯矩变形、剪切变形与转动惯量的影响;②桩周土土质均匀、各向同性,视为黏弹性连续介质,采用三参数Pasternak黏弹性地基模型模拟桩周土;③考虑桩-土相互作用受桩径大小的影响,假定桩侧摩阻力与各地基参数自桩顶至桩底均与桩径呈等比例线性变化,形成桩-土体系的计算模型,如图1所示。

图1 桩-土体系的计算模型
图1中:桩长为l;x为横向坐标;z为从桩顶沿竖向的坐标;t为时间;P为承台传递的轴向荷载。设任意z处截面中性轴上的横向位移为u(z,t),截面弯曲转角为φ(z,t);桩的弹性模量为Ep、质量密度为ρp、剪切模量为Gp、泊松比为νp、截面剪切修正系数为κ,均为常量,且有Gp=Ep/[2(1+νp)];桩横截面的周长、面积与惯性矩分别用up(z)、Ap(z)与Ip(z)表示,均为关于z的连续可微函数,设up(z)=up0h1(z),Ap(z)=Ap0h2(z),Ip(z)=Ip0h3(z),up0、Ap0、Ip0对应于桩顶横截面的周长、面积与惯性矩。对于圆锥形桩,其截面几何性质描述如下式
(1)
式中:d0为桩顶截面直径;m为描述截面几何性质变化的锥度系数,且0≤m<1。设锥形桩锥角为θ,桩顶截面半径为r0,则有:m=tanθ·l/r0。可知,当m值为零时,表示为等截面桩;当l/r0值一定时,m值越大,反映锥形桩的锥角越大。
图1(a)中,φ、γ、α分别为桩身微元段中性轴由纯弯矩引起的转角、由纯剪力引起的剪切角、由弯矩和剪力共同作用引起的转角,且φ=α-γ。图1(b)中:M(z,t)、Q(z,t)、N(z,t)分别为桩身任意深度z处横截面上的弯矩、剪力与轴力;fI(z,t)为由横向振动引起的单位长度横向惯性力;mI(z,t)为由横向振动引起的单位长度转动惯性力矩;Rs(z,t)为桩周土的地基反力。由Timoshenko梁理论可得如下关系[19]
(2)
(3)
(4)
(5)
设任意深度z处,轴向力N(z,t)始终与桩轴线方向相切,且不计桩自质量对轴向力的影响,N(z,t)>0表示为轴向压力;桩-土界面处的摩擦力用单位摩阻力f(z)表示,假定桩侧摩阻力随深度均匀线性变化,即
(6)
式中:f0为桩顶位置处对应的桩侧摩阻力;n1为比例系数。则深度z处桩横截面上的轴向力表示为
(7)
将式(1)的第1项与式(6)代入式(7),得

P-f0up0lh4(z)
(8)
式中,h4(z)为关于z的连续可微函数;可知,当f0=0时表示桩身不考虑土的竖向摩擦力影响,为端承桩。
由前述基本假定可得,微元体变形后,横截面上的水平向力H(z,t)与剪力Q(z,t)及轴向力N(z,t)的关系为[20]
(9)
土层任意深度z处,设桩周土模型的横向弹性系数、阻尼系数与剪切系数分别用k(z)、c(z)和g(z)表示。由三参数Pasternak黏弹性地基模型,可知
(10)
根据基本假定式(3),可设
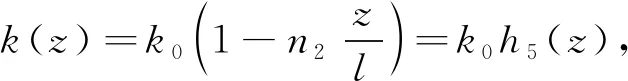
(11)
式中:k0、c0、g0分别为桩顶位置处对应的地基横向弹性系数、阻尼系数与剪切系数,分别反映桩周土的地基横向弹性刚度、阻尼效应与剪切刚度对桩身的作用;n2、n3、n4为比例系数。
1.2 锥形桩横向自由振动控制方程及边界条件
根据图1(b)微元段变形后的动力平衡条件即截面横向受力与弯矩的平衡,结合式(2)~式(5)、式(9)、式(10),推导出锥形桩横向自由振动的控制方程为
(12)
将式(1)、式(8)、式(10)、式(11)代入式(12),整理得
(13)

考虑自由振动问题,可设
u(z,t)=U(z)eλt,φ(z,t)=Φ(z)eλt
(14)
式中:U(z)、Φ(z)分别为桩身横向位移和截面弯曲转角的振型函数;λ为锥形桩的特征复频率;e为自然底数。
将式(14)代入式(13),则通过分离变量消除eλt项后,桩的横向自由振动控制方程转化为下式
(15)

(16)
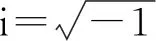
式(16)中系数项含有Ω2项,为便于求解方程组,引入2个新的变量函数Y1(ξ)、Y2(ξ),即
(17)
将式(17)代入式(16),并联立得如下方程组
(18)
为便于描述本文方法的求解过程,引入下列系数参量代入式(18)得式(19)。

(19)
式中:g(ξ)为方程组中不含特征值Ω的系数项;q为含特征值Ω的系数项;g(ξ)与q的第1个下标为微分方程组的方程,3为第3个方程,4为第4个方程;第2个下标为微分方程组中相应的函数,1为Y1(ξ),2为Y2(ξ),3为W(ξ),4为Φ(ξ);第3个下标为对应函数的导函数阶数,1为函数的一阶导数,2为函数的二阶导数。
关于桩端的边界条件,下面对固支(C)、铰支(H)、约束转角(P)和自由(F)4种边界约束条件对应的方程进行描述。
(1)对于固支边界条件,z=0或l位置:u(z,t)=0,φ(z,t)=0。无量纲化后,ξ=0与ξ=1处的边界条件方程为

(20)
(2)对于铰支边界条件,z=0或l位置:u(z,t)=0,M(z,t)=0。无量纲化后,ξ=0与ξ=1处的边界条件方程为

(21)
(3)对于约束转角边界条件,z=0或l位置:H(z,t)=0,φ(z,t)=0。无量纲化后,ξ=0与ξ=1处的边界条件方程为
(22)
(4)对于自由边界条件,z=0或l位置:H(z,t)=0,M(z,t)=0。无量纲化后,ξ=0与ξ=1处的边界条件方程为
(23)
至此,轴向荷载作用下黏弹性地基中锥形桩横向自由振动的固有频率及其对应振型函数求解问题,已经转化为求解满足相应边界条件方程式(20)~式(23)的变系数常微分方程组式(19)的一次特征值及其特征向量问题。
2 振动控制方程的微分求积法求解
由于锥形桩-土体系的振动控制方程式(19)及边界方程式(20)~式(23)中均含有变系数项,该类问题很难获得解析解,本文采用微分求积法进行数值解析。鉴于微分求积法对节点的离散形式较为敏感,基于数学角度,选取靠近边界的节点步长逐步减小的分布形式对减少权系数的截断误差、提高计算精度有利;基于力学角度,如刚度在端部附近区域发生突变或由于端部边界条件的影响,使得端点附近成为位移和内力变化最敏感的区域,在端部区域布置较多细密非均匀节点同样利于计算精度的提高。因此,本文采用非均匀分布的等比数列节点离散形式对ξ∈[0,1]区间进行节点变步长设置,如图2所示,对应节点离散公式如下[21]

图2 桩的离散模型
(24)
式中:ξi∈[0,1],区间分段数n取为偶数,q1为调节节点步长的公比,可根据边界条件与计算精度的需要调整,Zhang等给出了q1的合理取值范围,并验证了该类型节点与微分求积法中常用的以切比雪夫多项式根为节点具有相同的几何特征和计算精度。本文相关数值计算均取n=32,q1=1.2,后面不再赘述。
根据微分求积法原理,函数W(ξ)、Ф(ξ)在各节点上的导函数值可用(n+1)个节点对应函数值的加权线性求和来近似表示。函数及其相应导函数在各节点处的函数值用拉格朗日插值表示为
(25)
式中,lj(ξ)为拉格朗日插值多项式,即
(26)
对式(25)函数W(ξ)、Ф(ξ)分别求一阶导数,得
(27)
将式(27)中的ξ离散化,可知
(28)
依次类推,则
i,j=0,1,2,…,n
(29)

(30)
式(29)用向量形式表示为
(31)
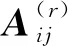
W(r)(ξi)={W(r)(ξ0),W(r)(ξ1),…,W(r)(ξn)}T,
W(ξj)={W(ξ0),W(ξ1),…,W(ξn)}T,
Φ(r)(ξi)={Φ(r)(ξ0),Φ(r)(ξ1),…,Φ(r)(ξn)}T,
Φ(ξj)={Φ(ξ0),Φ(ξ1),…,Φ(ξn)}T,
由函数微分关系
(32)
可得,函数各阶导数的加权系数矩阵之间的关系如下
(33)
将振动控制方程式(19)数值离散,并用向量形式表示,方程中的变系数项写成对角阵形式,即
G332=diag{g332(ξ0),g332(ξ1),…,g332(ξn)},
G331=diag{g331(ξ0),g331(ξ1),…,g331(ξn)},
G330=diag{g330(ξ0),g330(ξ1),…,g330(ξn)},
G340=diag{g340(ξ0),g340(ξ1),…,g340(ξn)},
G310=diag{g310(ξ0),g310(ξ1),…,g310(ξn)},
G431=diag{g431(ξ0),g431(ξ1),…,g431(ξn)},
G441=diag{g441(ξ0),g441(ξ1),…,g441(ξn)},
G440=diag{g440(ξ0),g440(ξ1),…,g440(ξn)},
Q310=diag{q310,q310,…,q310},
Q420=diag{q420,q420,…,q420}
结合式(31)、式(33),将振动控制方程式(19)转化为向量矩阵形式如下
(34)
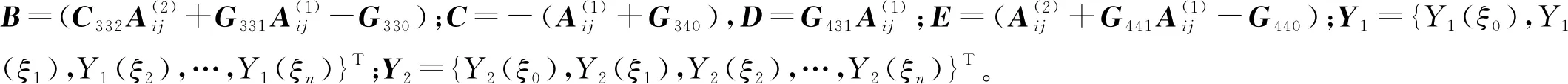
关于边界条件的处理,不失一般性地以桩顶约束转角、桩底固支边界条件(P-C)为例,对应边界条件方程的向量形式可写为
(35)
式中,[…]L为矩阵[…]的第L行元素。
式(34)由4个最高阶导函数为2阶的代数方程组成,可采用直接法引入式(35)中的4个边界条件方程。具体做法是分别用式(35)第1式中向量W前的行元素替换式(34)第3式中矩阵B的第1行元素,向量Ф前的行元素替换矩阵C的第1行元素、第3式的其余系数项矩阵的第1行元素均用数值0替换;用式(35)第2式中向量Ф前的行元素替换式(34)第4式中矩阵E的第1行元素,第4式的其余系数项矩阵的第1行元素均用数值0替换;用式(35)第3式中向量W前的行元素替换式(34)第3式中矩阵B的第(n+1)行元素,第3式的其余系数项矩阵的第(n+1)行元素均用数值0替换;用式(35)第4式中向量Ф前的行元素替换式(34)第4式中矩阵E的第(n+1)行元素,第4式的其余系数项矩阵的第(n+1)行元素均用数值0替换。
(36)
式(36)为含有(4n+4)个未知向量的一般线性代数特征方程组,进而应用QR分解技术进行数值计算,可同时得到一系列特征值Ω及其对应特征向量Y1、Y2、W、Φ,且均为复数形式。其中:Ω即为锥形桩的无量纲特征复频率;W、Φ为其对应的横向位移与弯曲转角的复振型,相应振型的虚部与实部分别用WI、WR与ΦI、ΦR表示。
3 算例与讨论
根据第2章微分求积法求解黏弹性地基中锥形桩横向自由振动控制微分方程组的方案,采用FORTRAN语言编制计算机程序进行数值计算,并在1 s以内完成相应问题的求解。下面先通过2个已知结果的算例验证目前方法的适用性,进一步分析各相关参数及比例系数对桩固有特性的影响。
3.1 数值算例对比验证
3.1.1 等截面Timoshenko梁的横向自由振动
当式(16)中无量纲参量m=β=k=c=g=0时,模型退化为等截面Timoshenko梁的横向自由振动问题。表1列举了当无量纲参量r=0.01、s=0.031 2、p=0时,不同边界条件下等截面Timoshenko梁前5阶无量纲固有频率。由表1可知,本文解与Tang等的精确解几乎完全吻合,验证了目前方法在求解不同边界条件下等截面Timoshenko梁横向自由振动固有频率良好的适用性与高精度。此外,与Zhang等的解相比,本文方法的区间分段数n明显较小,求解一般线性代数特征方程组矩阵的阶数为132×132,而Zhang等的解为324×324。可见,在达到同等精度条件下,目前方法的计算效率优于Zhang等的解。

表1 不同边界下,等截面Timoshenko梁横向自由振动前5阶固有频率(r=0.01, s=0.0312, p=0)
3.1.2 黏弹性地基上锥形梁的横向自由振动
当不考虑桩-土界面摩擦力影响,且桩周土的地基参数沿桩纵向为常量即式(16)中无量纲参量β=0,n1=n2=n3=n4=0时,模型退化为三参数Pasternak黏弹性地基上锥形Timoshenko梁的横向自由振动问题,梁的几何性质同式(1)。表2列举了无量纲参量r=0.002 5,s=0.012 5,p=0.25,k=2.5,g=0.246时,不同边界条件下梁的前3阶无量纲固有频率及对应衰减系数,并与Zhang等的研究进行对比,相关数值结果高度吻合。可见,目前方法适用于求解三参数黏弹性地基上变截面Timoshenko梁的横向自由振动问题。此外,由表2可知,边界条件、锥度系数与地基阻尼系数对梁的各阶固有频率及其衰减系数均有较大影响;相同参数下,梁的各阶频率相差较大,而衰减系数相差相对较小。

表2 不同边界下,三参数Pasternak黏弹性地基上锥形Timoshenko梁横向自由振动前3阶固有频率及其衰减系数(r=0.002 5, s=0.012 5, p=0.25, k=2.5, g=0.246; n=32, q1=1.2)
3.2 黏弹性地基中锥形桩横向自由振动特性分析
参照文献[22-23]进行桩-土体系的参数取值,设均质黏弹性地基中,圆截面锥形桩的弹性模量Ep=2.0×1010N/m2,质量密度ρp=2.5×103kg/m3,泊松比νp=0.17,桩顶截面半径r0=d0/2=0.15 m,桩长l=1.8 m,截面剪切修正系数κ=0.75;桩周土的弹性模量Es=4.0×106N/m2,质量密度ρs=2.0×103kg/m3,泊松比νs=0.4。参照Liu等的研究,取桩顶处桩侧摩阻力的初值f0=100 kPa;取桩顶承受轴向压力的初值为P=100 kN;考虑桩顶平台的影响,将桩顶边界条件近似为转角约束。对应地基参数,k0按经验公式取值[24],即
k0=1.2Es
(37)
根据文献[25]提供的c0参数建议取值范围,确定无量纲参数c的取值范围为[0, 0.1];设无量纲参数g的值范围为[0, 0.1],当g=0时,桩周土模型退化为动力Winkler模型。根据上述已知条件,相应无量纲参数为:r=1.736×10-3,s=5.417×10-3,p=2.207×10-4,β=3.744×10-4,k=0.034 3 , 取初值c=g=0.02。在具体数值计算中,为便于参数分析,由桩侧摩阻力随楔角增大而增大,取比例系数n1=-m;由Voigt体的弹性系数、粘壶系数与桩径成正比[26],取比例系数n2=n3=n4=m。
表3给出了3种边界条件下,锥度系数m=0和m=0.5时桩的前5阶无量纲固有频率及其衰减系数。其中,固有频率为欠阻尼自振频率;对应衰减系数为负值反映了地基阻尼对桩位移输出响应的衰减特性,数值越小,位移振幅衰减越快。由表3可知:桩顶约束转角时,固有频率随桩底约束的减弱明显降低,而对应衰减系数小幅增大;桩顶直径相同时,锥形桩较等截面桩的固有频率降低,而对应衰减系数增大,描述了桩身沿纵向逐渐变柔后固有特性的显著变化;相同参数时,各阶固有频率相差较大,而衰减系数相差微小,反映本文锥形桩-土体系可近似视为比例阻尼系统。
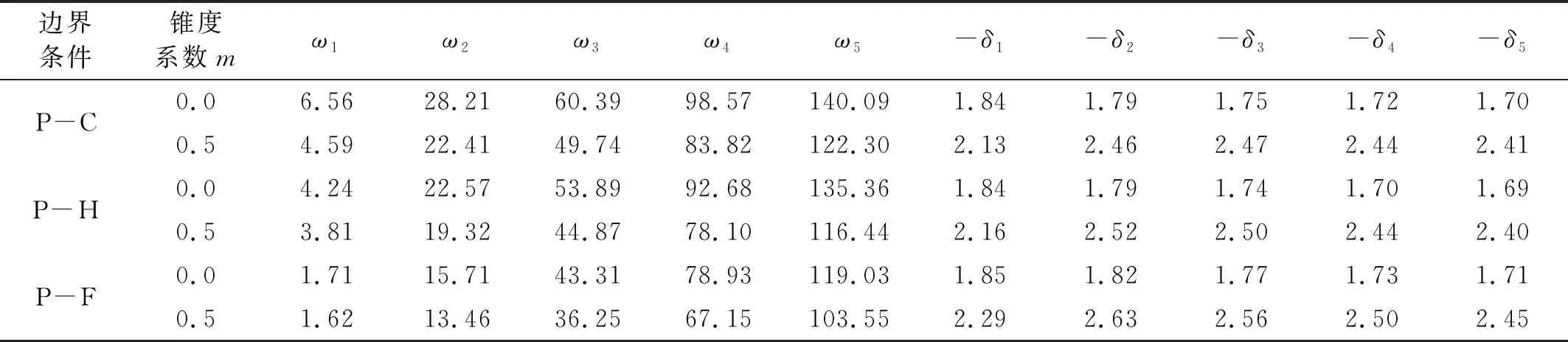
表3 不同边界下,桩的前5阶无量纲固有频率及其衰减系数(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)
3.2.1 锥角与地基阻尼对桩固有特性的影响
由式(1)可知,当桩长与桩顶截面半径之比l/r0不变时,锥形桩的锥角与锥度系数成正比,可通过调整锥度系数m值分析锥角θ对桩固有频率及其振型的影响。
图3、图4分别描述了欠阻尼状态下,3种边界条件桩前2阶固有频率及其衰减系数随锥度系数在[0, 0.85]内变化的关系曲线。由图3可知:桩顶约束转角时桩底约束越强,基频越大,对应衰减系数越小;基频及其衰减系数均随锥度系数的增加而降低,且降幅受边界条件影响显著,P-C边界基频降幅最大而衰减系数降幅相对较小,P-H边界基频降幅较小而衰减系数降幅居中,P-F边界基频降幅最小而衰减系数降幅相对较大。由图4可见:P-C边界与P-H边界第2阶固有频率均随锥度系数的增加而降低,P-C边界降幅较大,而P-F边界随锥度系数的增加先降后增;3种边界第2阶衰减系数均随锥度系数的增加呈明显的非线性降低。结合图3与图4来看:考虑到常见锥形桩的楔角小于2°即当m≤0.5时,固有频率及其衰减系数随楔角的增加而降低,数值上该降幅2阶高于1阶,且受边界条件影响较大。

图3 不同边界下,桩第1阶无量纲固有频率及衰减系数随锥度系数的变化关系曲线(r=1.736×10-3, s=5.417×10-3,p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)
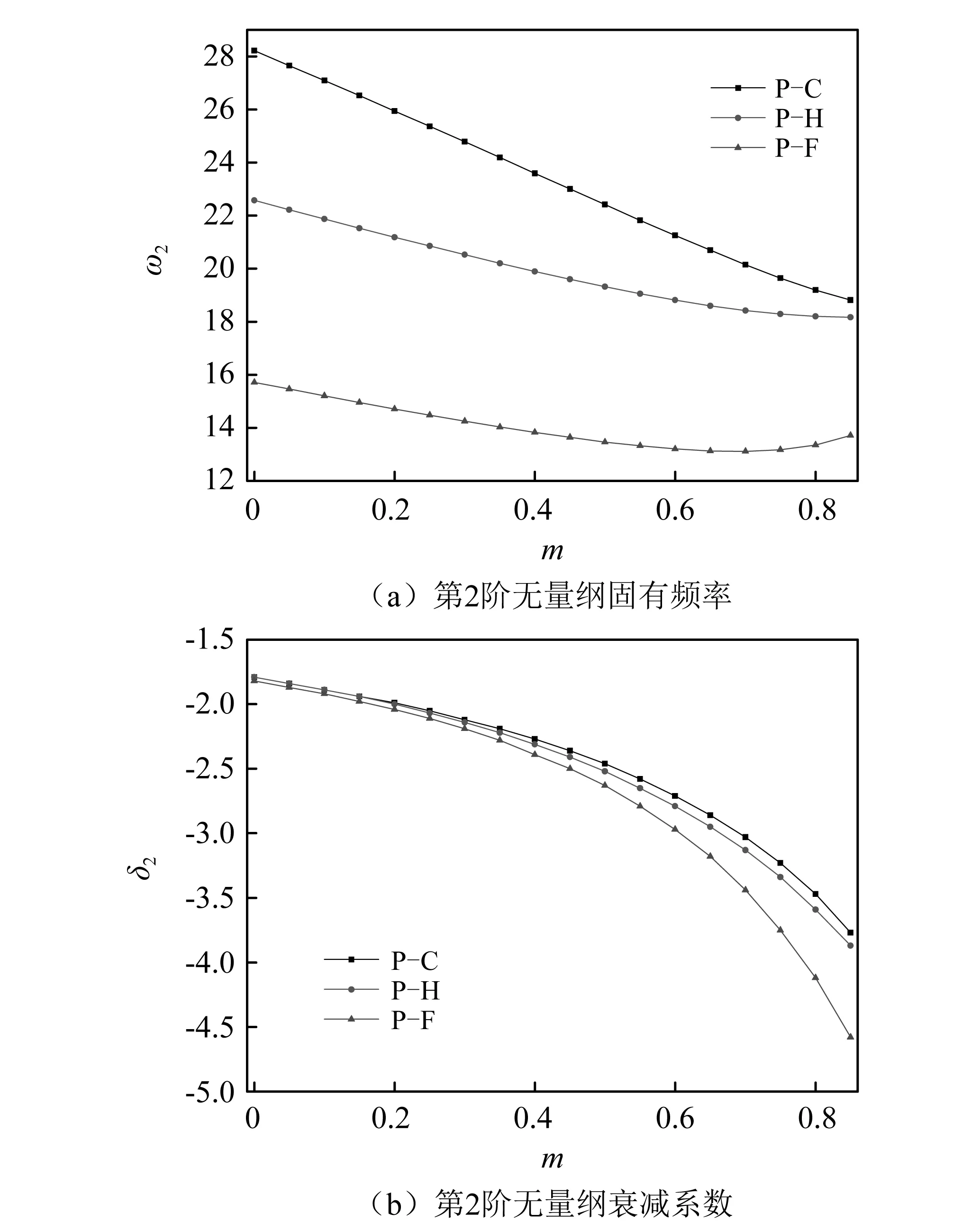
图4 不同边界下,桩第2阶无量纲固有频率及衰减系数随锥度系数的变化关系曲线(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)
以P-C边界为例,图5、图6分别刻画了等截面桩(m=0)与锥形桩(m=0.5)前3阶桩身截面横向位移与弯曲转角振型的虚部与实部。在给定边界条件与参数范围内,桩顶直径相同时,由图5(a)、图6(a)来看:锥形桩第1阶位移与转角幅值明显大于等截面桩,最大位移幅值位于桩顶,最大转角幅值向桩底偏离;第2、第3阶相差并不大,且最大位移幅值不在桩顶处。由图5(b)、图6(b)可知:锥形桩第1、第3阶衰减幅值明显低于等截面桩,第2阶衰减幅值则高于等截面桩,这表明在欠阻尼状态下地基阻尼对锥形桩基频响应的影响较大,而对高频响应的影响并不突出。

图5 P-C边界,桩的前3阶截面横向位移振型(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)

图6 P-C边界,桩前3阶截面弯曲转角振型(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4=m)
图7反映了P-C边界桩顶直径相同时,不同锥度系数m下桩的无量纲基频ω1及其衰减系数δ1随无量纲地基阻尼系数c的变化曲线。由图7(a)可知:在欠阻尼状态,m=0,0.1,0.3,0.5时对应的无量纲基频ω1均随无量纲地基阻尼系数c的增大而非线性降低,直至c=ccr达到各自临界阻尼状态时ω1刚好为0,之后随着c继续增大,桩进入过阻尼状态,此时ω1≡0,桩不发生振动而变为纯衰减运动,最后停止运动[27];取相同的c值,锥度系数m值越大,欠阻尼状态下基频越小,进而衰减振动周期越长;m=0,0.1,0.3,0.5达到各自临界阻尼状态对应的无量纲临界阻尼分别为ccr=0.074 15,0.068 14,0.057 16,0.047 52。由图7(b)可见:在c

图7 P-C边界,不同锥度系数下桩无量纲基频及对应衰减系数随地基阻尼系数的变化关系曲线(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, g=0.02; n1=-m, n2= n3= n4= m)
此外,图8描述了P-C边界m=0.5且c∈[0, 0.03]的欠阻尼状态下,不同比例系数n3时桩的无量纲基频ω1随c值的变化曲线,n3>0表示桩周土的横向阻尼系数自桩顶至桩底逐渐线性减小,n3=0表示不变,n3<0表示线性增大。由图8可知:c值较大时,桩周土地基阻尼系数沿桩身的变化对其基频的影响不可忽略,需考虑由桩径线性减小引起桩周土阻尼作用的变化。

图8 P-C边界,不同比例系数n3下桩无量纲基频随地基阻尼系数的变化关系曲线(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, g=0.02; m=0.5, n1=-m, n2=n4=m)
3.2.2 地基横向弹性系数与剪切系数对基频的影响
图9、10分别反映了P-C边界m=0.5及不同比例系数n2与n4时,欠阻尼状态下桩周土无量纲地基横向弹性系数k与剪切系数g对桩的无量纲基频ω1的影响关系曲线,n2及n4>0表示桩周土的横向弹性刚度与剪切刚度自桩顶至桩底逐渐线性减小,n2及n4=0表示不变,n2及n4<0表示线性增大。由图9、图10来看:欠阻尼自振基频ω1均随着k值与g值的增加而增大,进而衰减振动的周期随k值与g值的增加反而减小;考虑k值或g值自桩顶至桩底逐渐线性增大时(n2或n4<0),基频ω1值高于均匀分布(n2或n4=0);考虑k值或g值自桩顶至桩底逐渐线性减小时(n2或n4>0),基频ω1值低于均匀分布。此外,数值结果表明桩周土无量纲地基横向弹性系数k与剪切系数g对其衰减系数几无影响。

图9 P-C边界,不同比例系数n2下桩无量纲基频随地基横向弹性系数的变化关系曲线(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, c=g=0.02; m=0.5, n1=-m, n3= n4= m)

图10 P-C边界条件,不同比例系数n4下无量纲基频随地基剪切系数的变化关系曲线(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, β=3.744×10-4, k=0.034 3, c=0.02; m=0.5, n1=-m, n2=n3=m)
3.2.3 桩-土界面摩擦力、轴向荷载与桩长径比对基频的影响
图11描述了P-C边界m=0.5及不同比例系数n1时,欠阻尼状态下桩的无量纲基频ω1随无量纲桩侧摩阻力β值的变化曲线,n1=0表示桩侧摩阻力自桩顶至桩底不变,n1<0表示线性增大。由图11可见:桩的基频随桩周土摩阻力的增加而增大,且-n1值越大,基频的增幅越大;β值很小时影响并不明显,但β值较大时不考虑桩-土界面摩擦力的影响会低估桩的固有频率。此外,数值结果表明桩-土界面摩擦力对其衰减系数几无影响。

图11 P-C边界,不同比例系数n1下桩无量纲基频随桩侧摩阻力的变化关系曲线(r=1.736×10-3, s=5.417×10-3, p=2.207×10-4, k=0.034 3, c=g=0.02; m=0.5, n2=n3=n4=m)
图12刻画了P-C边界桩顶直径相同时,欠阻尼状态下不同锥度系数m对应的桩无量纲基频ω1随桩顶无量纲轴向荷载p的变化曲线。由图12来看:ω1随p值的增加而快速减小,且减幅随m值的增加而增大,当ω1减小至0时桩发生屈曲,此时轴向荷载为其屈曲临界荷载pcr;m=0,0.1,0.3,0.5时对应的无量纲屈曲临界荷载分别为pcr=0.075 8,0.065 4,0.047 2,0.032 0,即锥度系数越大,对应锥形桩的屈曲临界荷载越小。这表明随着桩身沿纵向逐渐变柔使其整体刚度降低,故而桩的屈曲稳定性显著降低。此外,数值结果表明桩顶轴向荷载对其衰减系数并无影响。

图12 P-C边界,不同锥度系数下桩无量纲基频随轴向荷载的变化关系曲线(r=1.736×10-3, s=5.417×10-3, β=3.744×10-4, k=0.034 3, c=g=0.02; n1=-m, n2=n3=n4= m)
设锥形桩的桩长与桩顶直径的比值为其长径比即μ=l/d0,以桩顶直径不变为前提,可通过调整桩长反映长径比的变化。可知,当m值一定且不为零时,随着桩长增大,锥角逐渐减小;相关无量纲参数中r、s随桩长的增加而减小,k、β值随桩长的增加而增大,c、g、p保持不变。为便于比较,将无量纲固有频率ω转化为含量纲的固有角频率,并用λI表示。可得
(38)
图13刻画了P-C边界桩顶直径相同时,欠阻尼状态下不同锥度系数m对应的桩基频λI1随桩长径比μ的变化曲线。由图13可知:桩的自振基频随桩长径比的增加先快速降低后缓慢降低,进而趋于稳定;当μ<10时锥度系数与长径比的耦合作用对基频影响较大,当10<μ<20时该耦合作用对其基频的影响逐渐减小,当μ>20时该耦合作用对其基频的影响可以忽略不计。这表明随着桩长径比的增大,一方面桩身截面剪切变形与转动惯量的影响逐渐降低即由Timoshenko梁逐渐向Euler-Bernoulli梁逼近;另一方面桩身锥角也逐渐减小,使得锥形桩的基频逐渐趋向于等截面桩。此外,数值结果表明桩长径比μ增加使基频λI1对应衰减系数λR1有微小增长,可忽略不计,在此不再赘述。

图13 P-C边界,不同锥度系数下桩基频随其长径比的变化关系曲线(p=2.207×10-4, c=g=0.02; n1=-m, n2=n3=n4=m)
4 结 论
基于Timoshenko梁理论,利用桩身微元体变形后的受力平衡条件建立了三参数Pasternak黏弹性地基中锥形桩的动力学模型,通过2个数值算例验证了目前方法的适用性。进一步,应用微分求积法分析了圆截面锥形桩的横向自由振动特性。以锥度系数衡量桩身锥角的变化,同时考虑轴向荷载、桩-土截面摩擦力及其沿桩身线性分布、桩长径比、地基参数及其沿桩身分布情况等对桩固有特性的影响,重点探讨了P-C边界条件下桩的自振基频及其衰减系数随锥角与地基阻尼的变化规律。在给定参数范围内,得到主要结论如下:
(1) 桩顶约束转角时,固有频率随桩底约束的减弱明显降低,而衰减系数小幅增大;相同参数时,各阶固有频率相差较大,而衰减系数相差微小,反映桩-土体系可近似视为比例阻尼系统。
(2) 当锥度系数m≤0.5时,桩的固有频率及其衰减系数随锥角的增加而降低,且受边界条件影响较大。随着地基阻尼的逐渐增大,锥形桩经历欠阻尼、临界阻尼和过阻尼状态,且锥角越大,临界阻尼越小。表明锥角与地基阻尼的有明显的耦合效应。
(3) 桩周土的地基横向弹性刚度、剪切刚度与地基阻尼较大时,对于锥形桩需考虑由桩径变化引起桩-土相互作用沿桩身纵向分布的不均匀性。
(4) 桩的基频随桩侧摩阻力的增加而增大,桩侧摩阻力较大时不考虑桩-土界面摩擦力的影响会低估桩的固有频率。
(5) 桩长与桩顶直径一定时,随着锥角的增大,桩身沿纵向逐渐变柔使其整体刚度降低,桩的屈曲临界荷载明显减小;桩顶直径一定时,桩的自振基频随桩长的增加先快速降低后缓慢降低,进而趋于稳定。

