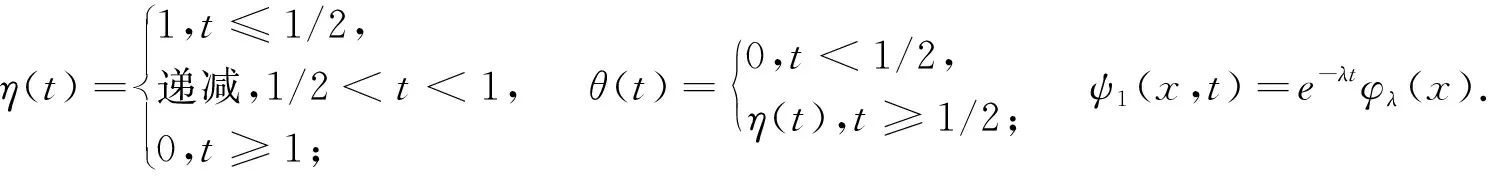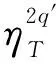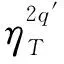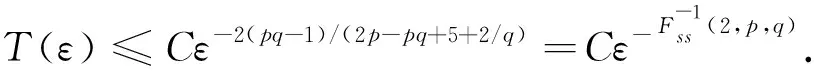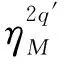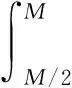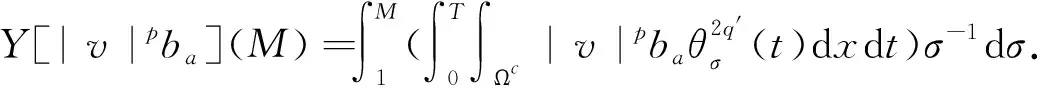一类波动方程耦合方程组解的破裂*
杜嘉仪, 明森, 杨婕, 苏业芹
(1.中北大学 数学系,山西 太原 030051;2.中北大学 大数据学院,山西 太原 030051;3.西南财经大学 证券与期货学院,四川 成都 611130)
1 引言
近来,波动方程解的破裂性态及其生命跨度的估计引起广泛关注[1-8].利用Kato引理,文[3]得到二维带幂次型非线性项波动方程解的破裂,但未给出解的生命跨度估计.文[4]证明了外区域上二维波动方程的初边值问题解的破裂性态.利用检验函数方法建立了解的生命跨度的上界估计.文[5]利用检验函数方法和迭代方法研究了带阻尼项的波动方程耦合方程组的小初值问题,其中非线性项为幂次型非线性项|v|p,|u|q.得到次临界和临界情形解的破裂以及生命跨度的上界估计.
本文利用检验函数方法研究如下非线性波动方程耦合方程组的初边值问题.
(1)
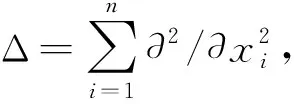

其中,0<ε<ε0,Γss(2,p,q)=max{Fss(2,p,q),Fss(2,q,p)}≥0,C是与ε无关的正常数.
下面给出证明定理1时需用到的一些引理以及问题(1)弱解的定义.
引理1[4]存在函数φ0(x)=ln(r/r0)满足
引理2[4]存在λ0∈(0,1/(2r0)),使得∀λ∈(0,λ0),φλ(x)满足
并且
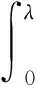
∂tba(x,t)=-ba+1(x,t),
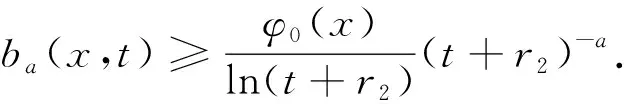
引理4[4]令λ∈(0,λ0),记q′=q/(q-1).则有
引理5[4]假设2 其中,δ、K1、K2>0,p1、p2>1.若p2 定义1若(u,v)是问题(1)的弱解,则(u,v)∈(C([0,T),H1(Ωc))∩C1([0,T),L2(Ωc)))2且 并且 (2) (3) 证明令 记ηT(t)=η(t/T),θM(t)=θ(t/M),M∈R+.计算得到 (ψ1)t=-λψ1,(ψ1)tt=λ2ψ1=Δψ1. (4) (Ⅰ)次临界情形Γss(2,p,q)>0 (5) 经计算可知 运用Hölder不等式及引理1,有 (6) 结合(5)式和(6)式可得 (7) (8) 利用Hölder不等式及引理4,可得 (9) (10) 由(8)-(10)式得到 (11) 类似于(7)式和(11)式的推导,有 (12) (13) 利用(7)式和(12)式,有 (14) 结合(11)式和(14)式,可得 (Ⅱ)临界情形Γss(2,p,q)=0,p≠q 记a=1/2-1/q.将(11)式代入(12)式中,并结合引理3,可得 (15) (16) 利用Hölder不等式、引理1及引理3,可得 (17) (18) 由(16)-(18)式得 (19) 结合(12)式和(19)式,有 (20) (21) 计算可得 (22) 利用(20)-(22)式,得到 (23) 利用(15)式、(21)式、(23)式和引理5,选取p1=pq,p2=pq-p+1,δ=εpq,从而得到T(ε)≤exp(Cε-q(pq-1)).同理可得T(ε)≤exp(Cε-p(pq-1)).因此,T(ε)≤exp(Cε-min(p(pq-1),q(pq-1))). (Ⅲ)临界情形Γss(2,p,q)=0,p=q 利用(11)式、(21)式及引理3,有 (24) 其中a=1/2-1/p.由(16)式和引理3可得 所以 (25) 于是,由(21)式、(22)式和(25)式得 Yp(M)≤C(lnM)p-1MY′(M). (26) 结合(24)式、(26)式及引理5,选取p1=p2=p,δ=εp,从而可得T(ε)≤exp(Cε-p(p-1)). 本文将文[4]中研究的问题推广为耦合方程组情形,利用非负截断函数构造检验函数得到问题(1)次临界及临界情形解的生命跨度估计,简化了文[5]中利用迭代方法得到的部分结果.另外,当问题(1)中p=q时,本文结果完善了文[3]中解的生命跨度估计.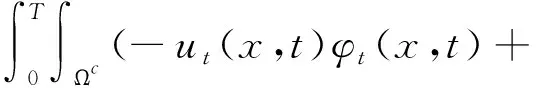
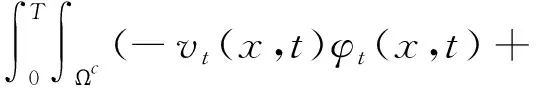
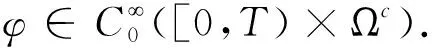
2 定理1的证明