粘弹性材料特慢蠕变的局部结构导数本构模型

管佩瑶,梁英杰

(河海大学 力学与材料学院,南京 211100)

自然界中,除弹性固体和粘性流体之外,还有一种介于二者之间的复杂物质,即粘弹性物质。塑料、橡胶、油漆、树脂、玻璃、陶瓷、混凝土以及金属等工业材料,岩土、土壤、沥青、石油和矿物等地质材料,肌肉、骨骼、血液等生物材料,常同时具有弹性和粘性两种不同机理的形变,综合地体现粘性流体和弹性固体两者的特性,称之为粘弹性材料。力学模型可以简单、直观地刻画材料的本构关系。通常假设粘弹性材料具有线性粘弹性特征,可以利用线弹性和理想粘性的叠加来描述材料的粘弹性行为。弹性元件和粘性元件的串联或者并联可以产生不同的效果,以此描述不同的粘弹性力学行为。由力学元件组合而成的力学模型可以同时表现出弹性性质和粘性性质,串并联特点类比于电路元件。最基本的粘弹性模型由一个弹性元件和一个粘性元件串联或者并联而成,这就是经典的Maxwell模型[1]和Kelvin模型[2]。传统的Maxwell和Kelvin模型中粘性元件的应力与应变率呈线性关系,为整数阶导数模型。整数阶导数模型在经典力学、声学、热传导、扩散、电磁学,甚至是量子力学中得到了较好的应用[3],但是物理学家和力学家也发现了越来越多的整数阶导数模型不能很好地解释的“反常”现象,例如复杂粘弹性材料的蠕变和松弛过程。当荷载持续时间较长时,材料的蠕变能导致内部结构的损伤,从而导致整体失稳或破坏[4]。因此,建立准确的粘弹性本构关系不仅能够有效地控制由于研究对象形变而产生的结构损伤和破坏,而且可以指导这些粘弹性材料在实际工程中的应用。

近年来,非整数阶导数模型是描述粘弹性本构关系的主要数学力学工具。蔡伟等[5]将分形导数应用到粘弹性建模中,推导了分形Maxwell和分形Kelvin模型的蠕变柔量和松弛模量,数值结果表明这些模型可以很好地描述扩展指数律依赖的粘弹性行为。分数阶导数蠕变和松弛本构模型[6-7]是描述幂律依赖粘弹性行为的主要方法,与分形导数相比,分数阶导数是一个积分算子,计算成本较高。分形导数模型和分数阶导数模型描述的这些扩展指数律和幂律依赖的粘弹性力学行为,称为反常力学行为。实验表明[8],复杂粘弹性材料的蠕变或者松弛不满足传统的指数律增长或衰减机制,也不满足扩展指数律和幂律,其力学行为为对数律依赖,称为特慢力学行为。而分形导数模型和分数阶导数模型均不能准确描述特慢力学行为。

目前,常用于研究粘弹性材料特慢蠕变的模型是传统的Lomnitz模型[9],但是传统的Lomnitz模型只是一个经验模型,不能通过解析推导得到相应的蠕变函数。为更好地描述粘弹性材料特慢蠕变的现象,通常在传统整数阶导数模型的基础上添加更多的弹簧元件和牛顿粘壶,以此获得较好的拟合效果。然而,这样的处理方式导致在本构方程中引入了更多的材料参数,也使得本构关系具有复杂的形式。另外,苏祥龙等[10]建立了一种非局部结构导数模型,运用于描述混凝土的特慢力学行为,但是该建模方法包含积分计算,计算成本较高。杨旭等[11]以逆Mittag-Leffler函数为结构函数建立了局部结构粘壶,用于描述混凝土的特慢蠕变,由于逆Mittag-Leffler函数没有解析表达式,该模型不方便推广使用。为解决上述问题,文中将采用局部结构导数[11]进行建模。

通过引入新的结构函数,基于传统模型对牛顿粘壶的应变率进行修正,提出了一种新的局部结构导数建模方法,发展准确描述粘弹性材料特慢力学行为的本构模型。与现有的常用于描述复杂系统的非局部分数阶导数相比,局部结构导数没有积分计算,为计算模拟节约了大量的计算成本。特别地,传统整数阶导数和分形导数均是文中所提局部结构导数的特例。传统整数阶导数的结构函数是线性函数,分形导数的结构函数是幂函数,而文中局部结构导数建模方法使用的结构函数为对数函数。

文中第一部分简要介绍了现有的传统整数阶模型和分形导数模型,并推导了局部结构导数模型,对比了不同粘壶的本构方程;第二部分以Maxwell本构模型为基础,介绍了传统整数阶模型和分形导数模型的蠕变和松弛方程,推导了局部结构导数,并对比了不同模型的蠕变柔量和松弛模量;第三部分通过3组混凝土蠕变实验数据,验证了局部结构导数模型,并与不同模型进行了对比;第四部分对文中工作进行了总结。

1 粘弹性材料建模方法

1.1 传统整数阶模型

在传统整数阶模型中,弹性元件应力与应变呈线性关系,粘性元件应力与应变率呈线性关系[1],即

式中:E为弹性模量,η为粘性系数。这里的弹性元件由弹簧表示,粘性元件由牛顿粘壶表示,如图1所示。

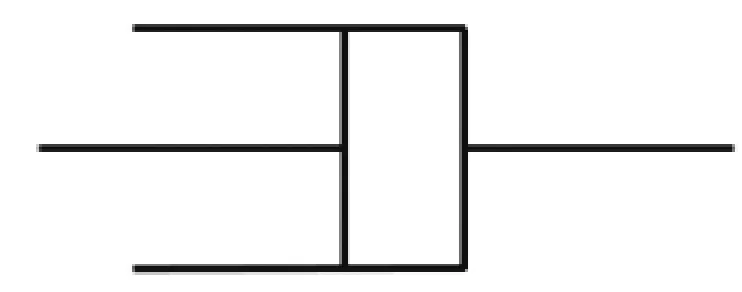
图1 牛顿粘壶Fig.1 Newtonian dashpot

传统整数阶Maxwell模型由弹簧和牛顿粘壶串联而成,传统整数阶Kelvin模型由弹簧和牛顿粘壶并联而成,如图2所示。

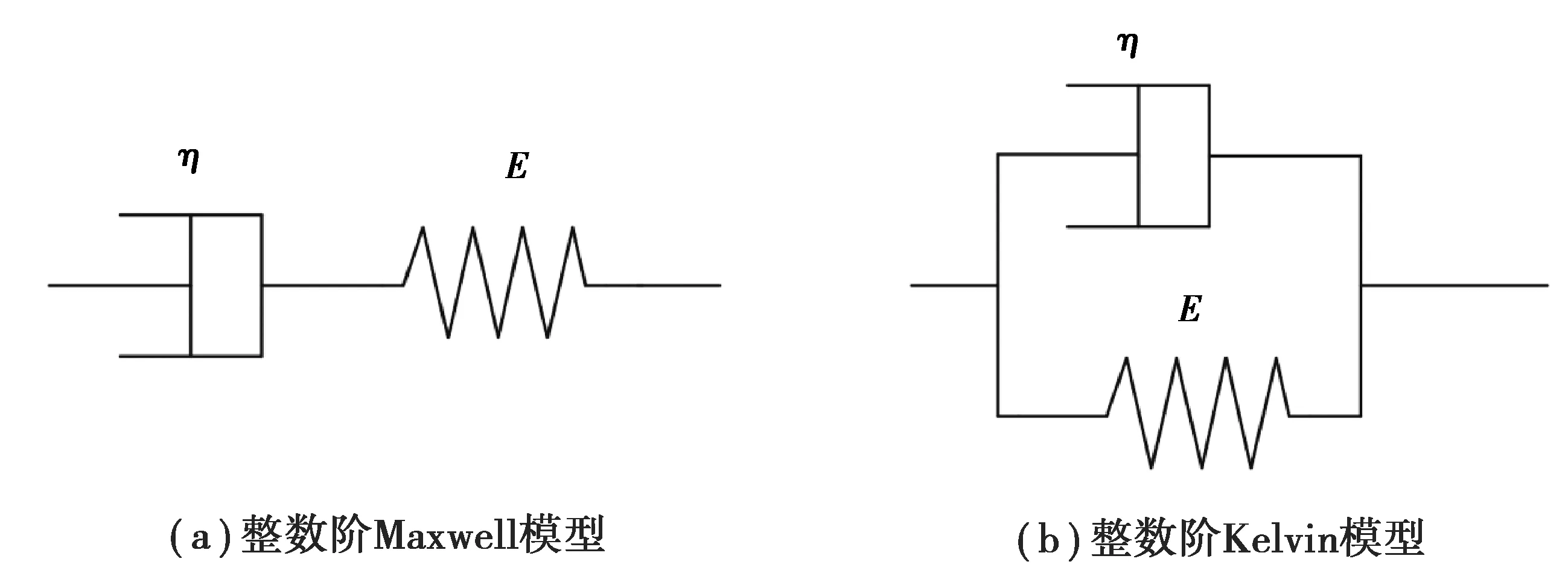
图2 整数阶Maxwell模型和整数阶Kelvin模型示意图Fig.2 Schematic diagrams of integer order Maxwell model and integer order Kelvin model

在传统整数阶Maxwell模型中,总应力与粘性元件、弹性元件各自应力相等,总应变为2部分应变之和,由此可以得到传统整数阶Maxwell模型所描述的本构方程[1]为

类似的,在Kelvin模型中,总应变与粘性元件、弹性元件各自应变相等,总应力为2部分应力之和。由此可以得到传统整数阶Kelvin模型所描述的本构方程[1]为

1.2 分形导数模型

分形导数基于时空变换的定义[12]为:

式中,α、β分别表示时间和空间上的分形导数的阶数。从定义式中可以看出,当导数的阶数取为1时,分形导数可以退化为经典的导数。蔡伟等[5]将分形导数应用到粘弹性建模中,用分形导数取代牛顿粘壶里的常规导数,得到一种分形粘壶,如图3所示。

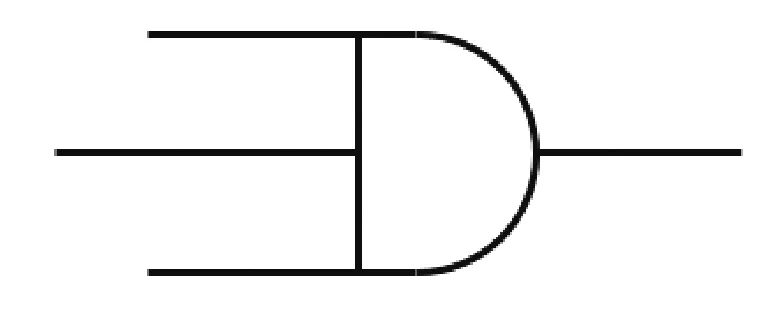
图3 分形粘壶Fig.3 Fractal dashpot

其本构关系为

式中,β是分形导数的阶数,代表一种分形维数。

分形粘壶与弹簧串联可得分形导数Maxwell模型,分形粘壶与弹簧并联可得分形导数Kelvin模型,如图4所示。

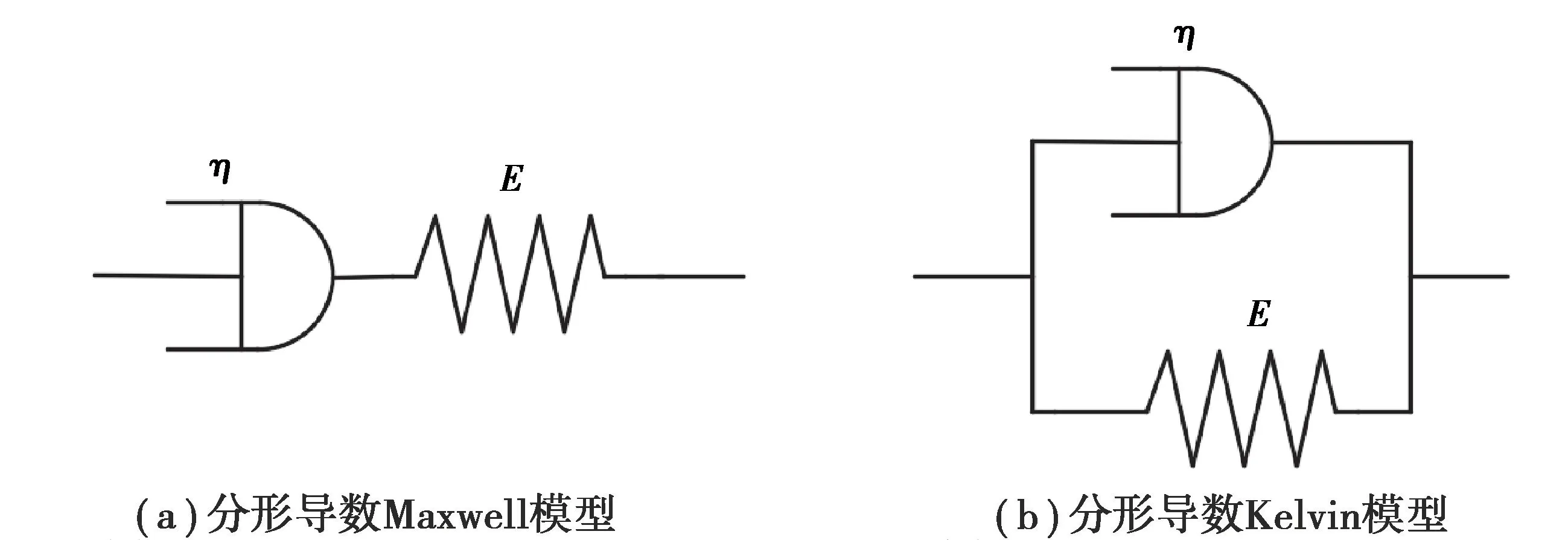
图4 分形导数Maxwell模型 和分形导数Kelvin模型示意图Fig.4 Schematic diagrams of fractal derivative Maxwell model and fractal derivative Kelvin model

与传统整数阶模型类似,可以得到分形导数Maxwell模型的本构方程和Kelvin模型的本构方程[13],为

式中,β表示分形导数的阶数,0＜β＜1。当β=1时退化成传统整数阶模型。

1.3 局部结构导数模型

通过引入新的结构函数,提出了一种局部结构导数建模方法。

给定函数u(t),以时间为变量,其局部结构导数的定义[14]为

式中B(t)为结构函数。特别地,当B(t)=tβ时,局部结构导数退化为分形导数;当B(t)=t时,局部结构导数退化为整数阶导数。

文中采用式(11)作为结构函数,构造局部结构导数本构模型为

式中,τ0为对t无量纲化的处理。在局部结构导数建模方法中,用结构粘壶(见图5)替代传统粘壶[11],即可得到对应的局部结构导数粘弹性模型。

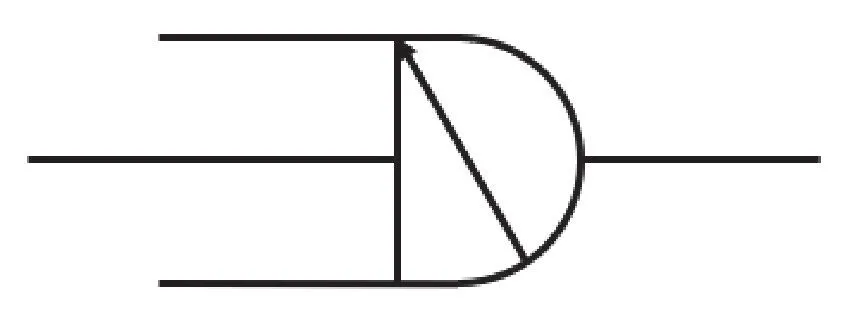
图5 结构粘壶Fig.5 Structural dashpot

结构粘壶的本构关系为

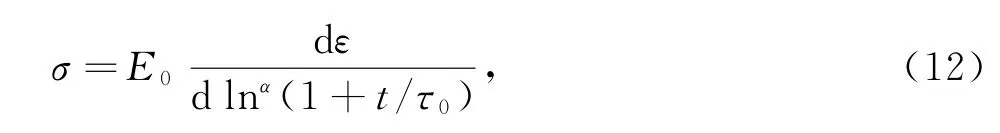
式中:E0为粘性模量;α为结构导数的阶数。将结构粘壶与弹簧串联或者并联可以得到局部结构导数Maxwell模型和Kelvin模型,如图6所示。

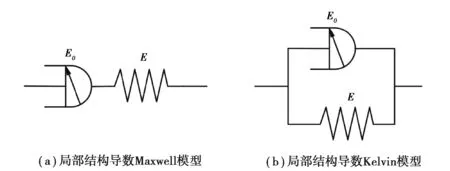
图6 局部结构导数Maxwell模型和局部结构导数Kelvin模型示意图Fig.6 Schematic diagrams of local structural Maxwell model and local structural Kelvin model

当结构粘壶与弹簧串联时,总应力与粘性元件、弹性元件各自应力相等,总应变为两部分应变之和,即

式中:下标e代表弹性元件;下标v代表粘性元件。由此可得局部结构导数Maxwell模型的本构方程为

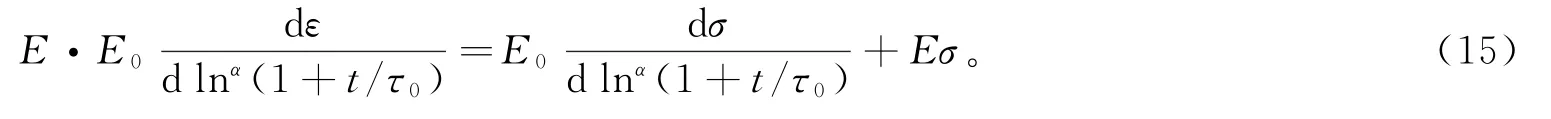
当结构粘壶与弹簧并联时,总应变与粘性元件、弹性元件各自应变相等,总应力为两部分应力之和,即:

由此可以得到局部结构导数Kelvin模型所描述的本构方程为

1.4 方法对比

表1给出了整数阶模型、分形导数模型和局部结构导数模型的对比结果。从模型的粘性元件构成来看,分形导数粘弹性模型是用分形粘壶替代整数阶粘弹性模型中的牛顿粘壶,局部结构导数粘弹性模型则是用结构粘壶替代牛顿粘壶。从模型的本构方程来看,当分形导数的β=1时,退化成整数阶模型。

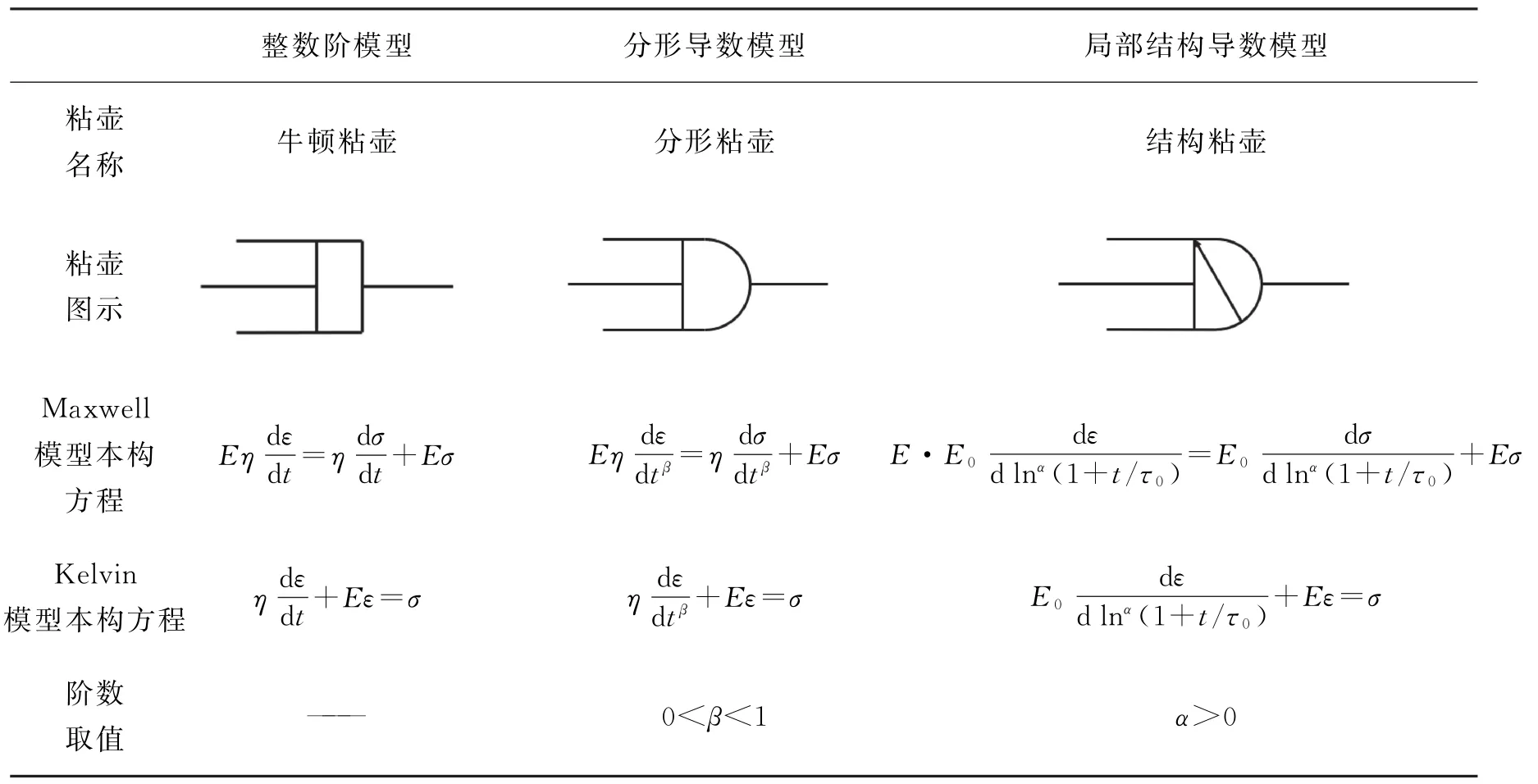
表1 3个模型对比图Table 1 Comparison of three models

表中:ε为应变,σ为应力,是实验测得参数;E为弹性模量,η为粘性系数,E0为粘性模量,三者都是材料参数;α为结构导数的阶数,β为分形导数的阶数,均可通过模型拟合实验数据获得;τ0为对t无量纲化的处理。

2 不同粘弹性模型下的蠕变和松弛行为

本节将根据局部结构导数本构方程推导对应的蠕变柔量和松弛模量。

2.1 局部结构导数Maxwell模型

根据式(15)局部结构导数Maxwell模型的本构方程,给定初始应力σ0,有

同时,当t=0 时,ε(t)=。将式(19)两边同时积分,得到蠕变过程:

蠕变柔量为

若在式(21)基础上,给定初始应变ε0,可得

将两边分离变量,得

再根据初始条件当t=0 时,σ(t)=Eε0,可得松弛过程

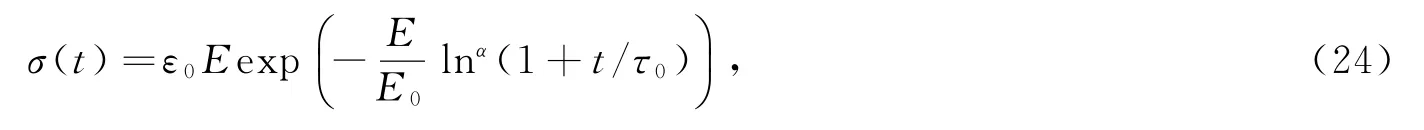
松弛模量为

表2给出了3种不同Maxwell模型的蠕变和松弛方程。

表2 3种不同Maxwell模型的蠕变和松弛对比Table 2 Comparison of creep and relaxation in three different Maxwell models

2.2 局部结构导数Kelvin模型

根据式(18)局部结构导数Kelvin模型的本构方程,给定初始应力σ0,有

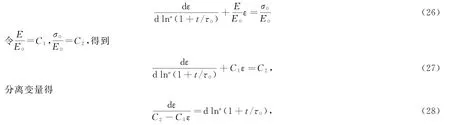
当t=0 时,ε(t)=0,由此求得C1、C2,再将两边同时积分,得到蠕变过程:

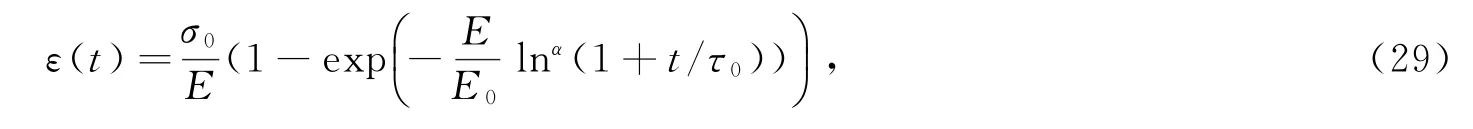
蠕变柔量为

若在式(18)基础上,给定初始应变ε0,可得松弛过程

表3给出了3种不同Kelvin模型的蠕变方程。

表3 3种不同Kelvin模型的蠕变对比Table 3 Comparison of creep in three different Kelvin models

2.3 对比和分析

根据上述松弛方程可知,Maxwell模型的松弛响应随时间增加而减小,当t较小时,松弛响应接近于弹性体;当t趋向于无穷时,松弛响应接近于牛顿流体。此外,传统整数阶Maxwell模型的蠕变响应表现为一条斜直线,这说明整数阶Maxwell模型在发生瞬时弹性的同时,产生稳定的流动,然而几乎没有材料的蠕变曲线是这种线性形式,因此很少有学者用该模型来模拟蠕变现象。整数阶Maxwell模型因而被称为松弛模型,主要用来描述松弛过程。

图7给出了不同Maxwell模型对应松弛模量的变化曲线。在下面的部分中,若没有特殊说明,参数分别设置为:弹性模量E=10,无量纲化τ0=2,粘性模量E0=100。局部结构导数模型阶数分别取典型值α=0.5和α=1。从图7可以看出,当t=0时,所有模型的松弛模量与弹性模量相等。短时期内4个模型差异较小,但在长期松弛过程中,整数阶模型衰减速率最快且最早达到稳定状态;分形导数衰减速率次之,局部结构导数衰减速率最慢。另外,局部结构导数模型阶数α=0.5的松弛过程衰减速率显著慢于阶数α=1的松弛过程。

图7 不同Maxwell模型对应松弛模量的对比Fig.7 Comparison of relaxation modulus in different Maxwell models

在Kelvin模型中,蠕变响应随时间增加而增加,并且当t趋向于无穷时,蠕变响应接近于弹性体。然而,Kelvin模型无法模拟应力松弛现象,因此Kelvin模型主要用来描述蠕变过程。

图8给出了不同Kelvin本构模型对应蠕变柔量的对比。与Maxwell松弛模量对比图类似,传统整数阶模型蠕变过程的增长速率最快,分形导数模型次之,局部结构导数模型的增长速率最慢,并且局部结构导数模型阶数α=0.5的蠕变过程增长速率显著慢于阶数α=1的蠕变过程。

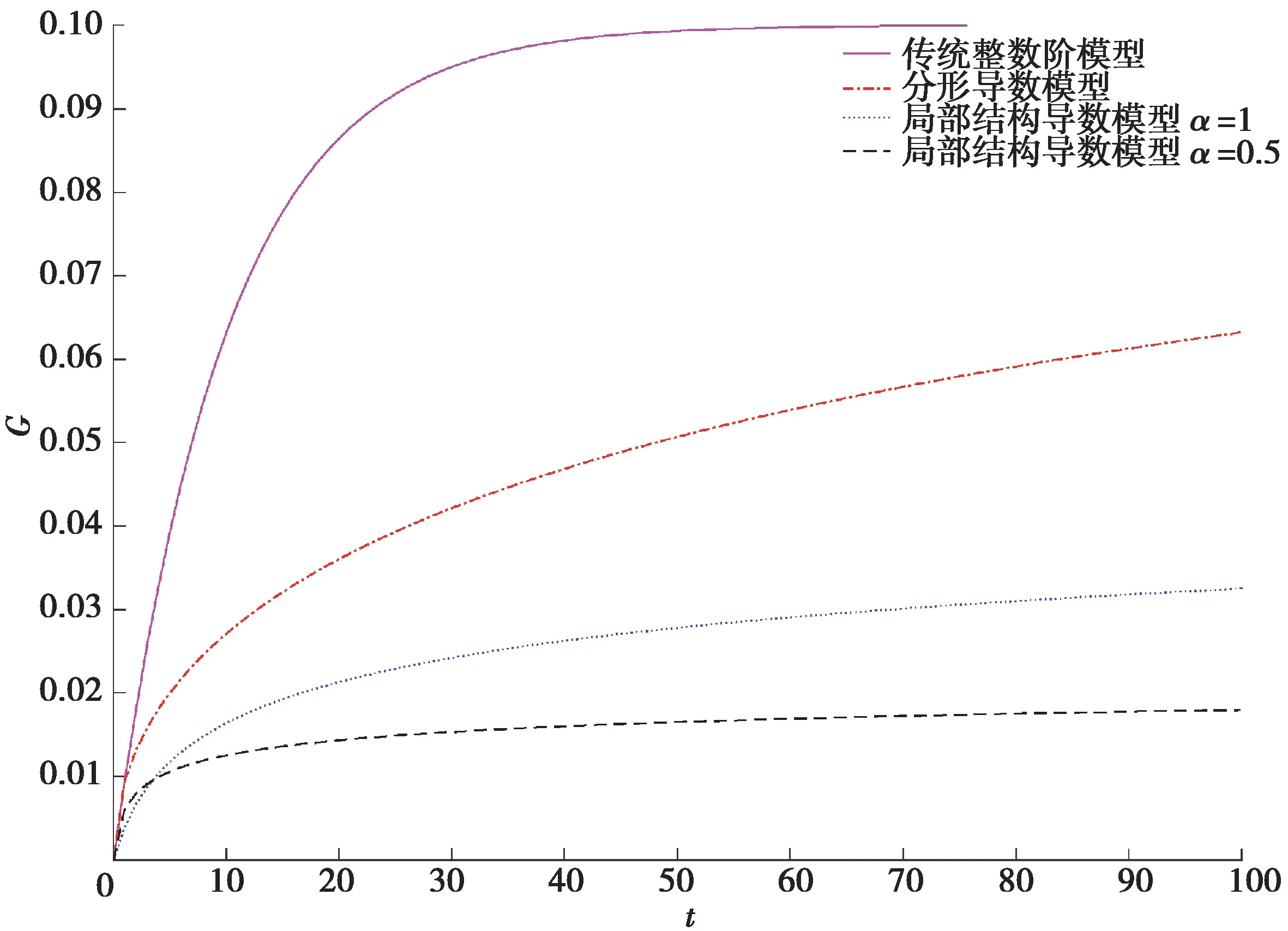
图8 不同Kelvin模型对应蠕变柔量的对比Fig.8 Comparison of creep modulus in different Kelvin models

由模型的理论结果表明,局部结构导数对应的Maxwell模型和Kelvin模型都能刻画粘弹性材料的较慢的蠕变和松弛现象。图9和图10分别给出了基于局部结构导数模型不同阶数对应的蠕变和松弛曲线,α分别取0.1、0.3、0.6、1。结果表明,当统一其他参数时,α取值越小,蠕变和松弛的速率越慢。α取值越接近于1,不同α之间的速率差异越大。α取值越小,蠕变或者松弛过程趋于稳定所需的时间越短。

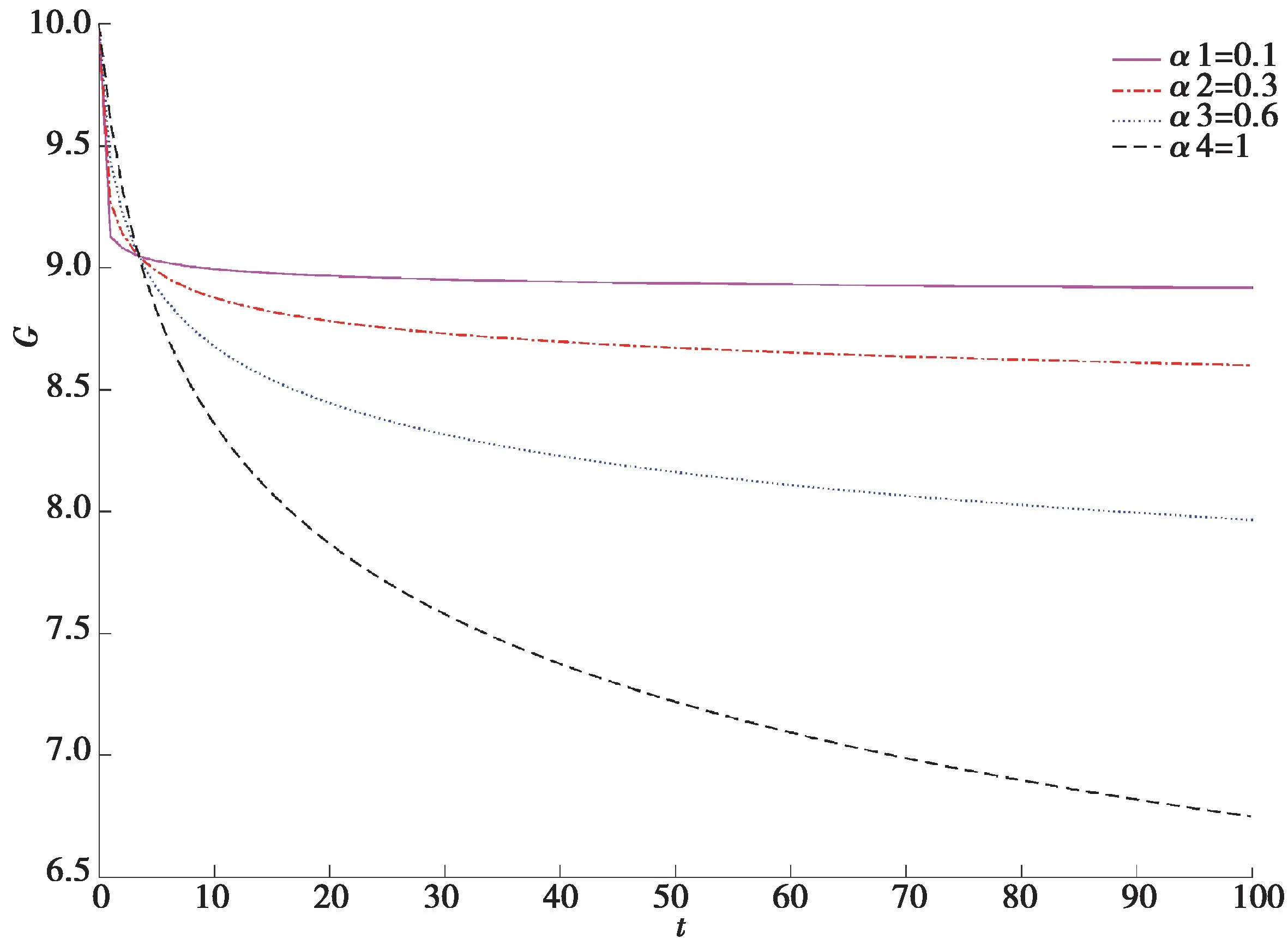
图9 局部结构导数Maxwell模型不同α 的松弛模量对比图Fig.9 Comparison of relaxation modulus in local structural derivative Maxwell model with different values ofα

图10 局部结构导数Kelvin模型不同α 的蠕变柔量对比图Fig.10 Comparison of creep modulus in local structural derivative Kelvin model with different values ofα

3 局部结构导数模型的应用

本节将采用3组混凝土的蠕变实验数据验证局部结构导数模型描述特慢蠕变的可行性。

第一组实验数据为高强自密实混凝土的蠕变实验数据。高强自密实混凝土与普通的高强混凝土相比,具有诸多的优点和施工优势。高强自密实混凝土不仅具有高强混凝土的优势,而且还具有自密实混凝土的特点,是一种新型的建筑材料。自密实混凝土在施工工艺方面具有节能、环保、降噪等特点,并且可以大大节省施工时间。文中选取文献[15]中高强自密实混凝土在16 h龄期、加载30%的强度应力比条件下的实验数据,用局部结构导数模型进行拟合分析,其结果见图11所示。

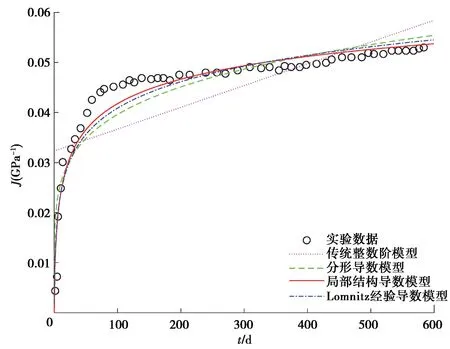
图11 传统整数阶模型、分形导数模型、局部结构导数模型和Lomnitz模型拟合第一组混凝土蠕变实验数据的对比图Fig.11 Fitting results for the first creep experimental data set of the concrete by using the classical integer order model,the fractal derivative model,the local structural derivative model and the Lomnitz model

第二组实验数据为混凝土长达12 a的蠕变实验数据,取自参考文献[16]。混凝土圆柱试样在房间20±1 ℃温度和50±5%相对湿度条件下,对混凝土圆柱试样进行加载,局部结构导数模型拟合结果如图12所示。

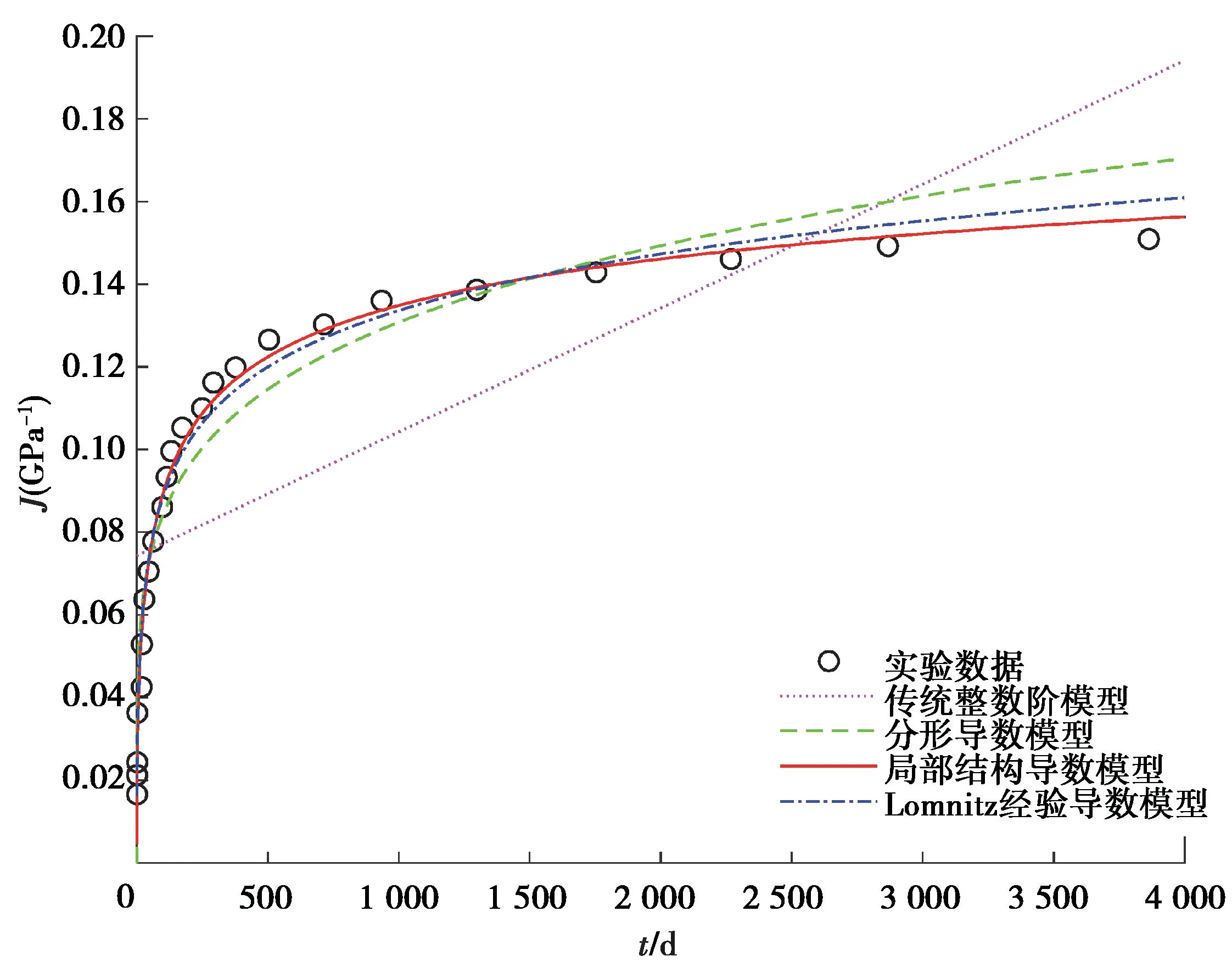
图12 传统整数阶模型、分形导数模型、局部结构导数模型和Lomnitz模型拟合第二组混凝土蠕变实验数据的对比图Fig.12 Fitting results for the second creep experimental data set of the concrete by using the classical integer order model,the fractal derivative model,the local structural derivative model and the Lomnitz model

第三组实验数据选取文献[17]中,高性能混凝土(UHPC)在90℃(194°F)下进行热处理,并在加载时以其拉伸强度的40%进行加载,以获得90 d的蠕变实验数据。拟合结果如图13所示。图中J是蠕变柔量,单位为GPa-1。

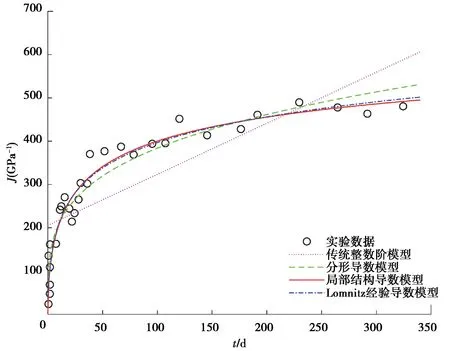
图13 传统整数阶模型、分形导数模型、局部结构导数模型和Lomnitz模型拟合第三组混凝土蠕变实验数据的对比图Fig.13 Fitting results for the third creep experimental data set of the concrete by using the classical integer order model,the fractal derivative model,the local structural derivative model and the Lomnitz model

需要指出的是,最早应用于研究粘弹性材料特慢蠕变的模型是传统的Lomnitz模型

式(32)这种对数蠕变律已被用来描述地幔的地震后变形[18]和岩石的流变学[19]。许多学者[20-23]研究了经典的Lomnitz模型并试图对其进行修改,但是这些模型不适用于描述广义的特慢流变现象。同时,Lomnitz模型只是一个经验模型,物理意义不明晰,无法通过解析解得到蠕变或者松弛过程的函数。

本节将同时对比基于Maxwell本构的传统整数阶模型、分形导数模型、局部结构导数模型和Lomnitz模型,描述上述3组混凝土实验中特慢蠕变力学行为的可行性。图11～图13分别给出了4种模型拟合3组混凝土实验对应蠕变柔量数据的结果。

从图11～图13中的拟合结果可以看出,传统整数阶模型呈线性变化趋势,与粘弹性材料性质不符。在实验初期,除了传统整数阶模型之外的3个模型都与实验数据吻合良好。在实验中期和末期,局部结构导数和Lomnitz模型表现得更好。Lomnitz模型可用于描述混凝土特慢蠕变的实验数据,但是该模型是一个经验模型,物理意义不清楚,不利于推广。与Lomnitz模型相比,局部结构导数模型在第一组和第二组实验数据拟合结果上,均有明显的优势,特别是第一组实验数据的拟合结果。对于第三组实验数据,两者的拟合结果相当。模型的参数通过最小二乘法确定,表4和表5分别给出了局部结构导数模型和Lomnitz模型参数的值。

表4 局部结构导数模型的参数值Table 4 The values of the parameters in the local structural derivative model

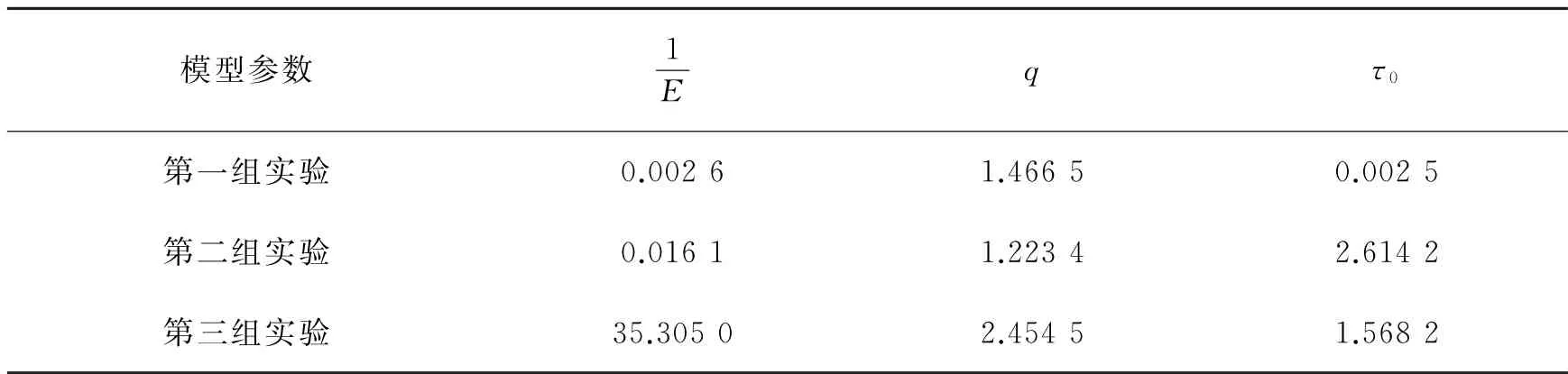
表5 Lomnitz模型的参数值Table 5 The values of the parameters in the Lomnitz model

仅从局部结构导数所描述的蠕变过程来说,实验时间越长,材料的应变越大,且应变呈对数律增加。当t=0时,其值为同等应力水平下不考虑粘性性质的材料应变大小,即为参数的大小。

对3组实验数据的拟合结果分别计算拟合优度,表6给出了不同模型拟合优度的对比,整数阶模型和分形导数模型的拟合优度较小,局部结构导数模型的拟合优度与Lomnitz模型的拟合优度接近。在第二组和第三组实验中,局部结构导数模型的拟合优度最高。结果表明,局部结构导数模型是可行的。

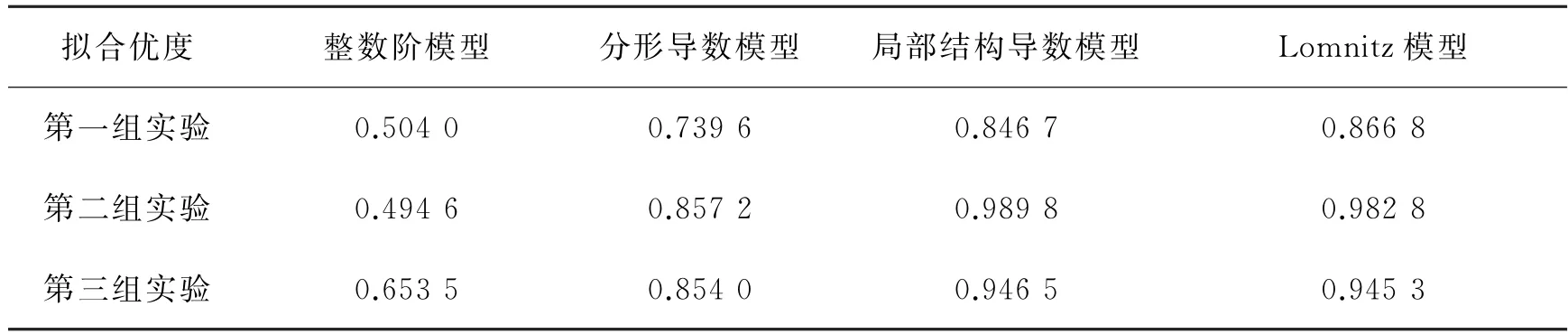
表6 不同模型的拟合优度对比Table 6 Comparison of goodness-of-fit in different models

4 结论

传统的整数阶模型适用于描述指数增长的蠕变过程,分形导数模型适用于描述扩展指数增长的蠕变过程,这两者均不能用于描述特慢蠕变的力学行为。Lomnitz模型虽然可以用于描述特慢蠕变的力学行为,但是它只是一个经验模型,物理意义并不十分明晰。通过上述研究,文中通过引入lnα(1+t/τ0)作为结构函数,建立的局部结构导数本构模型,能够更好地描述具有对数依赖现象的粘弹性材料特慢力学行为。通过3组混凝土蠕变实验数据,验证了其描述特慢力学行为的可行性。与传统整数阶模型、分形导数模型和Lomnitz模型相比,局部结构导数模型在刻画特慢蠕变力学行为方面具有明显的优势。

根据局部结构导数Maxwell模型本构方程,可得该模型无法描述初始应变为0的蠕变过程和初始应力为0的松弛过程。根据局部结构导数Kelvin模型本构方程,可得该模型只能描述初始应变为0的蠕变过程,并且无法描述粘弹性材料的松弛过程。结构粘壶也可描述初始应变为0的蠕变过程。

文中主要关注的问题是粘弹性材料的特慢蠕变力学行为建模,对特慢松弛模型的验证将在今后的工作进一步研究。其次,从数学形式的角度来说,Lomnitz模型是局部结构导数Maxwell模型的特殊形式。局部结构导数Maxwell模型为Lomnitz模型提供了明确的物理解释。因此,文中仅应用了局部结构导数Maxwell模型,并将其与其他模型进行对比,对局部结构导数Kelvin模型的应用将在今后的工作中完善。最后,以宏观模型和数学解析的方法描述粘弹性材料的力学行为,没有结合材料的微观结构,将在后面的研究做进一步分析和讨论。