具有完美匹配单圈图的无符号拉普拉斯系数和关联能量
葛春雨
(兰州交通大学 数理学院, 甘肃 兰州 730070)
本文考虑的图都是无向简单图。设图G的顶点集和边集分别为V(G)={v1,v2,…,vn}和E(G)={e1,e2,…,em}。图G的邻接矩阵A(G)=(aij)n×n定义如下:若顶点vi与顶点vj邻接,则aij=1;否则aij=0。度对角矩阵D(G)=diag(d(v1),d(v2),…,d(vn)),其中d(vi)为顶点vi的度。图G的无符号拉普拉斯矩阵Q(G)=D(G)+A(G)。设|E(G)|=m,图G的关联矩阵I(G)=(bij)n×m,当顶点vi是边ej的端点时,bij=1;否则bij=0。图G的关联能量[1]IE(G)是指关联矩阵I(G)的奇异值之和。Gutman等[2]指出图G的关联能量等于其所有无符号拉普拉斯特征值的平方根之和。
图G的无符号拉普拉斯特征多项式定义为
其中φi(G)为图G的无符号拉普拉斯多项式系数。
令Gn是包含所有n个顶点简单图的集合。令⪯是Gn上通过比较任意两个图的无符号拉普拉斯系数的大小所定义的偏序关系。对任意两个图G,H∈Gn,如果φi(G)≤φi(H)对所有的i=1,2,…,n成立,那么我们称G⪯H;若存在一个值i使得满足φi(G)<φi(H),则称GH。
文献[3]证明了所有n个顶点的单圈图构成的集合关于偏序⪯有两个极大元和两个极小元;Mirzakhah和Kiani[4]研究了单圈图的无符号拉普拉斯矩阵的系数,得到了n个顶点的单圈图恰有两个极小元和极大元;文献[5]讨论了所有n个顶点的双圈图构成的集合关于偏序关系⪯的极小元;文献[6]刻画了所有顶点数为n、匹配数为m的单圈图的集合关于偏序关系⪯的极小元;文献[7]刻画了n个顶点不含偶圈的连通图集合关于偏序关系⪯的极小元;更多关于单圈图的研究可参考文献[8-11]。受上述文献启发,本文主要研究具有完美匹配的单圈图的无符号拉普拉斯系数及其极图。
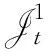
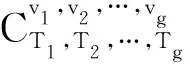
1 单圈图的无符号拉普拉斯系数

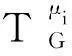
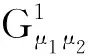

图1 G和





图2 G和
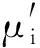

图3 G和G′
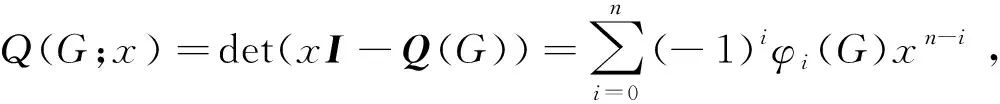
其中求和项取遍G的所有恰有i条边的TU-子图Hi。显然φ0(G)=1,φ1(G)=2m。
引理2[5]令G是一个n≥4个顶点的简单连通图。如果Gμv是由G通过α-变换[13]得到的,那么Gμv⪯G,即
φi(Gμv)≤φi(G),i=0,1,…,n,
等号成立当且仅当或者i∈{0,1,n}且G是非二部图,或者i∈{0,1,n-1,n}且G是二部图。

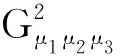
等号成立当且仅当i∈{0,1,n}。

等号成立当且仅当i∈{0,1,n}。
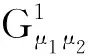
等号成立当且仅当i∈{0,1}。

f:H ′→H,H′→H=f(H′),
其中
V(H)=V(H′),
{μ1μ3|μ1μ3∈E(H′)}+{μ2μ3|μ1μ3∈E(H′)},
则f:H ′→H是单射。令N是H′中的不含顶点μ1、μ2的所有连通分支的权重。除了H′中包含μ1和μ2的分支,H′中其他任意一个分支对应H中的一些分支。分以下3种情形讨论。
情形1 若μ1μ2∈E(H′),则H′和H除了R′和f(R′)外有相同的连通分支,而且两个连通分支R′和f(R′)有相同的阶数,因此W(H)=W(H′)。
情形2 若μ1μ2E(H′),并且μ1包含在H′的一个奇单圈分支U′中,则H′中的两个分支{μ2}和R′对应着H中的一个树分支,通过单射f,得到H中树分支阶数至少为g。因此
W(H)-W(H′)≥g·N-4·1·N=N(g-4)≥0。
情形3 若μ1μ2E(H′),且T′是H′的一棵树。则H′和H除了R′和{μ2}外有相同的连通分支。定义通过单射f,H中有一个阶数为a+1阶的树分支对应于H′中阶数为a+b+1的分支T′,且H中有一个阶数为b+1阶的树分支对应于H′中的分支{μ2}。因此
W(H)-W(H′)=(a+1)·(b+1)·N-(a+b+1)·N=Nab≥0,
等号成立当且仅当a=0或b=0。由以上讨论和引理1知,当2≤i≤n,有

等号成立当且仅当i∈{0,1}。

f:H ′→H,H′→H=f(H′),
其中
V(H)=V(H′),
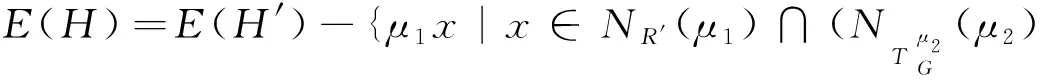

则f:H ′→H是单射。令N是H′中的不含顶点μ1、μ2的所有连通分支的权重。我们假设在包含μ1的连通分支H-μ1μ2-μ1v1有a1+1个顶点,在包含μ2的连通分支H-μ1μ2-μ2μ3-μ2v2有a2+1个顶点,且a1,a2≥0。
若μ1、μ2在H′的一个分支R′中。注意到H′中的一个分支R′对应着H=f(H′)中的一个分支f(R′)包含μ1;并且R′和f(R′)是树分支或奇单圈分支时有相同的阶数;同时除了H′中的一个分支R′,H′中的任意分支对应着H中的一些分支。因此W(H)=W(H′)。
若μ1、μ2在H′中的两个分支中,分以下两种情形讨论。
情形1R′是H′中的一棵树,类似于定理1的证明可得W(H)-W(H′)≥0。
情形2R′是H′的一个奇单圈分支,假设|V(R′)V(Cg-1)|=λ(λ≥0)。
定义H1={H′∈H ′|R′是一个奇单圈分支,且μ1、μ2、μ3在2或3个分支中}。
子情形2.1μ1v1E(H′),μ2v2E(H′)。
H′中的4个分支R′、{v1}、{μ2}和{v2}对应H=f(H′)的一个树分支R1(含μ1、μ2,且|R1|≥g)及{v1}和{v2},且H′和H除了这7个分支外有相同的分支,则
W(H)-W(H′)=(g+λ)·N-4·1·1·1·N≥N(g-4)≥0。
类似地,当μ1v1∈E(H′),μ2v2∈E(H′);μ1v1∈E(H′),μ2v2E(H′);μ1v1E(H′),μ2v2∈E(H′)时,通过与子情形2.1相同的分析,有W(H)-W(H′)≥0。
综上所述并结合引理1可得,当2≤i≤n时,
令Gg(s1,t1;s2,t2;…;sg,tg)是一个n个顶点的单圈图,它是在圈Cg:μ1μ2…μi…μgμ1的顶点μi(i=1,2,…,g)上连接si条长为2的悬挂路和ti条悬挂边得到的图。
定理3 (1)G3(s1,1;s2,1;s3,1)G3(s1+s2+s3,1;0,1;0,1),n≥6;
(2)G3(s1,1;s2,0;s3,0)G3(s1+s2+s3,1;0,0;0,0),n≥4;
(3)G3(s1,1;s2,0;s3,0)G3(0,1;0,0;s1+s2+s3,0),n≥4;
(4)G4(s1,0;s2,0;s3,0;s4,0)G4(s1+s2+s3+s4,0;0,0;0,0;0,0),n≥4;
(5)G4(s1,1;s2,1;s3,1;s4,1)G4(s1+s2+s3+s4,1;0,1;0,1;0,1),n≥8;
(6)G4(s1,1;s2,1;s3,0;s4,0)G4(s1+s2+s3+s4,1;0,1;0,0;0,0),n≥6;
(7)G4(s1,0;s2,1;s3,1;s4,0)G4(s1+s2+s3+s4,0;0,1;0,1;0,0),n≥6。
证明下面仅证定理3中的(4),其余各款的证明与(4)的证明类似,这里不再赘述。
令G′=G4(s1+s2+s3+s4,0;0,0;0,0;0,0)是由G=G4(s1,0;s2,0;s3,0;s4,0)通过γ-变换所得到的图(如图3所示)。要证GG′,仅需证φi(G)≥φi(G′),对所有的i=0,1,…,n等号成立。显然i∈{0,1,n}时,φi(G)=φi(G′)。下面假设2≤i≤n-1。令H ′和H分别是G′和G的恰有i条边的TU-子图的集合。显然H ′和H中没有奇单圈分支。令H ′=H′(1)∪H′(2)∪H′(3)∪H′(4),其中H′(j)(j=1,2,3,4)是μ1,μ2,μ3,μ4属于j个不同分支的TU-子图。
对任意的TU-子图H′∈H ′,记R′是H′的含μ1的连通分支。令
f:H ′→H,H′→H=f(H′),
其中
V(H)=V(H′),
E(H)=E(H′)-{μ1x|x∈NR′(μ1)∩NG(μ2)}-{μ1x|x∈NR′(μ1)∩NG(μ4)}-
{μ1x|x∈NR′(μ1)∩NG(μ3){μ2,μ4}}+{μ2x|x∈NR′(μ1)∩(NG(μ2)}+
{μ4x|x∈NR′(μ1)∩NG(μ4)}+{μ3x|x∈NR′(μ1)∩NG(μ3){μ2,μ4}},

令N是H′中不含{μ1,μ2,μ3,μ4}所有分支的权重。记μ1μ2=e1,μ2μ3=e2,μ3μ4=e3,μ4μ1=e4。下面分4种情形分别讨论。
情形1H′∈H′(1),如果e1、e2、e3、e4中至少有3条边属于E(H′),那么μ1、μ2、μ3、μ4在一个分支中,则W(H)=W(H′),即
情形2H′∈H′(4),若e1、e2、e3、e4∉E(H′),则μ1、μ2、μ3、μ4在4棵树中,则W(H)-W(H′)=N[ab(cd+c+d+1)+ac(d+1)+ad+bc(d+1)+bd+cd]≥0,即
情形3H′∈H′(3),若μ1、μ2、μ3、μ4在3棵树中,则W(H)-W(H′)=[(a+b+2)(c+1)(d+1)+(a+d+2)(b+1)(c+1)+(a+1)(b+1)(c+d+2)+(a+1)(d+1)(b+c+2)-6(a+b+c+d+2)]N≥0,即
情形4H′∈H′(2),若μ1、μ2、μ3、μ4在2棵树中,则W(H)-W(H′)=[b(a+c+d+2)+d(a+b+c+2)+c(a+b+d+2)+a(b+c+d+2)+(a+b)(c+d)+(a+d)(b+c)]N≥0,从而
因此不等式φi(G)≥φi(G′)对所有i=0,1,2,…,n-1,n均成立。
Mirzakhah和Kiani在文献[4]中建立了图的关联能量与无符号拉普拉斯系数之间的关系如下:
引理5[4]令G和H是n个顶点的两个图,若G⪯H,则IE(G)≤IE(H),若GH,则IE(G) 本文主要通过比较图的无符号拉普拉斯系数的大小,借助几种可以保持偏序关系⪯的图变换,确定了具有完美匹配的单圈图集中关于偏序关系的极小元和具有最小关联能量的极值图。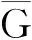

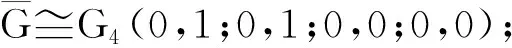


3 总结

