基于矩阵快速填充的P-FFT分析目标电磁散射问题研究
朱锦新 郑永涛 孔维宾 毕奥燃


摘 要:针对预修正快速傅里叶变换(P-FFT)方法的近场矩阵填充速度和效率不高的问题,利用快速填充技术减少近场矩阵的计算时间,分析电大目标的电磁特性。采用预修正快速傅里叶变换方法,不仅能够减少存储需求,而且能够加快远场的矩阵矢量积。重点研究了基于三角形配对的快速填充方法,通过提取基函数测试配对积分过程中的共享积分部分,对近场矩阵元素进行填充,提高了计算效率。数值结果表明,基于三角形配对的预修正快速傅里叶变换方法可以减少近场部分的计算时间,从而提高算法的效率。
关键词:矩量法;预修正快速傅里叶变换方法;电磁散射;近场矩阵
中图分类号:TP311 文献标识码:A
Research on Analyzing Electromagnetic Scattering Problems of Targets by P-FFT based on Matrix Fast Filling
ZHU Jinxin, ZHENG Yongtao, KONG Weibin, BI Aoran
(School of Information Technology, Yancheng Institute of Technology, Yancheng 224051, China)
Abstract: Aiming at the low filling speed efficiency of the near-field matrix in the P-FFT (Pre-corrected Fast Fourier Transform) method, this paper proposes to use fast filling technique to reduce calculation time of the near-field matrix, which is used to analyze the electromagnetic characteristics of the electrically large target. The P-FFT method not only reduces storage requirements, but also speeds up the far-field matrix-vector product. The fast filling method based on triangle pairing is mainly studied. By extracting the shared integral part of the paired integration process of the basis function test, the near-field matrix elements are filled and the calculation efficiency is improved. Numerical results show that the P-FFT method based on triangle pairing can reduce the computation time of the near-field part, thereby improving the efficiency of the algorithm.
Keywords: method of moment; pre-corrected fast Fourier transform method; electromagnetic scattering; near-field matrix
1 引言(Introduction)
矩量法作為一种精确的数值方法,被广泛应用于分析各种复杂的电磁问题[1-2]。然而,矩量法的存储量和计算量都很大,限制了求解电磁问题的规模。为了解决矩量法的局限性,许多人开始研究基于矩量法的快速算法。快速算法大体上可以分为两类:一类是与积分核相关的算法,如快速多级子算法(FMM)[3]、多层快速多极子(MLFMA)[4-5]和多层格林函数插值方法(MLGFIM)[6],以及基于快速傅立叶变换的方法,如自适应积分方法(AIM)、预修正快速傅里叶变换方法(P-FFT)、积分方程快速傅里叶变换(IE-FFT)等[7-11]。另一类是矩阵压缩方法,如自适应交叉逼近(ACA)算法[12]、骨架化[13]等。
本文提出了一种结合近场矩阵快速填充的预修正快速傅里叶变换(P-FFT)方法来分析电大目标的电磁特性。采用P-FFT方法可加快矩阵矢量乘法的求解速度。此外,阻抗矩阵存储稀疏,减少了内存需求。同时,采用基于三角形配对的快速填充方法生成近场矩阵,能够提高计算速度。
2 理论基础(Theoretical basis)
2.1 矩量法
为了用矩量法数值求解电场积分方程(EFIE)和磁场积分方程(MFIE),首先将导体表面划分为三角形,然后用RWG基函数展开式表示的电流密度代入:
3 数值结果(Numerical results)
在本部分中给出了两个数值算例,以验证P-FFT方法的效率和准确性。在基于快速傅里叶方法的快速算法中选择笛卡尔网格间距相等,即hx=hy=hz=h,展开的阶数为M。
3.1 球体
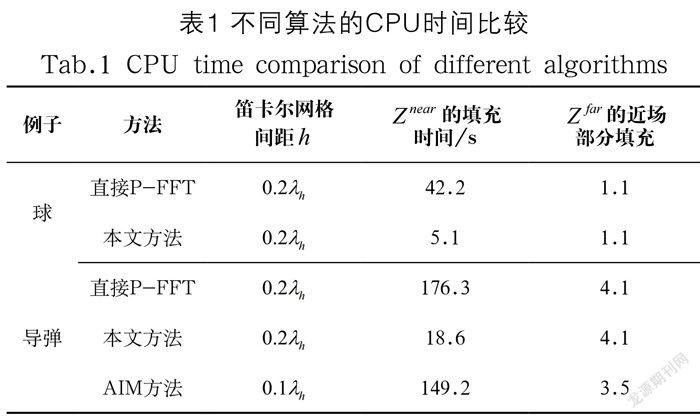
如图2所示为一个半径为2λh的PEC球。球的雷达散射截面使用Mie级数和P-FFT计算。球面使用1/10波长离散,共产生18,468 个RWG基函数。计算所得双站RCS曲线被显示在图3上。从图3中可以看到,三条曲线是一致的,这说明了基于三角形填充的P-FFT的正确性。从表1可以看出,本文提出的方法比直接P-FFT在填充近场矩阵速度上具有很大的优势。
3.2 导弹模型
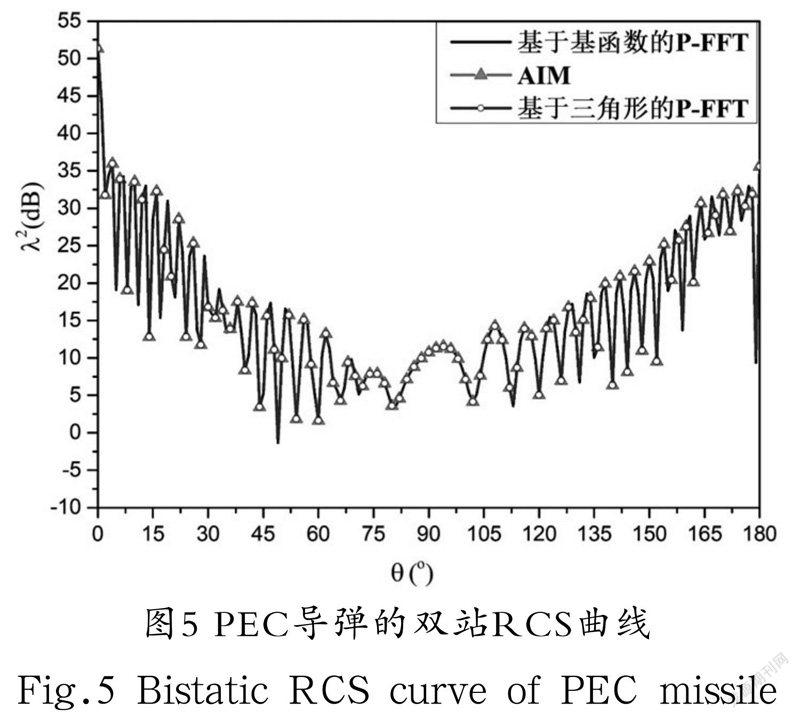
如图4所示,给出了一个PEC导弹模型。导弹被剖分为98,475 个RWG基函数。从图5中可以看出,基于基函数填充的P-FFT、AIM和基于三角形填充的P-FFT的计算结果的曲线是吻合的,说明基于三角形填充的P-FFT在计算复杂结构的物体电磁散射问题上是正确的。在表1中,本文方法与AIM、基于基函数填充的P-FFT在近场矩阵填充的速度上进行了对比,结果表明本文方法的计算效率得到了提高。
4 结论(Conclusion)
本文采用P-FFT方法结合快速填充方法求解電磁场积分方程,通过引入一种三角形配对的方式,提取其中的积分共享部分填充矩阵元素。从本文所给的数值算例可以看出,三角形配对的采用,减少了近场矩阵元素计算的时间,从而提高了预修正所需要的计算效率。
参考文献(References)
[1] HARRINGTON R F. Field computation by moment methods[M]. New York, NY, USA: MacMillian, 1968:20-26.
[2] 李弘祖,郭立新,董春雷,等.基于八叉树优化的MoM-PO/PTD混合算法分析目标电磁散射及辐射问题[J/OL].系统工程与电子技术.[2021-8-17].https://kns.cnki.net/kcms/detail/11.2422.TN.20210817.0947.002.html.
[3] ENGHETA N, MURPHY W D, ROKHLIN V, et al. The fast multipole method (FMM) for electromagnetic scattering problems[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(6):634-641.
[4] SONG J M, LU C C, CHEW W C. Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(10):1488-1493.
[5] DELGADO C, CATEDRA F. Fast monostatic RCS computation using the near-field sparse approximate inverse and the multilevel fast multipole algorithm[J]. Applied Computational Electromagnetics Society, 2020, 35(7):735-741.
[6] LI L, WANG H G, CHAN C H. An improved multilevel Green's function interpolation method with adaptive phase compensation[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(6):1381-1393.
[7] BLESZYBSKI E, BLESZYNSKI M, JAROSZEWICZ T. AIM: Adaptive integral method for solving large-scale electromagnetic scattering and radiation problems[J]. Radio Science, 1996(31):1225-1251.
[8] PHILLIPS J R, WHITE J K. A Precorrected-FFT method for electrostatic analysis of complicated 3-D structures[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1997(16):1059-1072.
[9] SEO S M, LEE J F. A fast IE-FFT algorithm for solving PEC scattering problems[J]. IEEE Transactions on Magnetics, 2005, 41(5):1476-1479.
[10] 韩晓冰,张潇,王露洁,等.采用分部外推BCGS-FFT方法快速求解电磁散射问题[J/OL].电波科学学报.[2021-8-17].https://doi.org/10.13443/j.cjors.20 20 081801.
[11] LI M, CHEN R S, WANG H, et al. A multilevel FFT method for the 3-D capacitance extraction[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2013, 32(2):318-322.
[12] LI M, SU T, CHEN R S. Equivalence principle algorithm with body of revolution equivalence surface for the modeling of large multiscale structures[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(5):1818-1828.
[13] RASOOL H, CHEN J, PAN X M, et al. Skeletonization accelerated solution of Crank-Nicolson method for solving three-dimensional parabolic equation[J]. Applied Computational Electromagnetics Society, 2020, 35(9):1006-1011.
作者简介:
朱锦新(1978-),男,硕士,讲师.研究领域:计算智能,计算机并行计算.
郑永涛(1998-),男,硕士生.研究领域:系统与自动控制.
孔维宾(1982-),男,博士,副教授.研究领域:计算电磁学,智能算法,电子信息.
毕奥燃(1999-),男,本科生.研究领域:电子信息,智能控制.

