多自由度球轴承与轴的刚度耦合分析与计算*

张耀虎,马临超,齐山成

(1.北京新联铁集团股份有限公司,北京 100044;2.河南工业大学 机电学院,河南 郑州 450000;3.郑州机械研究所有限公司,河南 郑州 450000)

0 引 言

目前,球轴承已经在铁路机车、船舶、汽车、拖拉机、重型机械等动力传动系统中得到了广泛应用。

作为传动系统中的重要零部件,球轴承的性能是否优良对系统的传动精度有着重要的影响。

球轴承刚度是球轴承重要的使用性能指标之一,因此,对其刚度进行计算与分析很有必要,尤其是对球轴承的径向刚度和轴向刚度进行计算与分析更有必要。

对球轴承刚度的计算属于典型的非线性方程求解问题。JONES A B在Hertz球轴承的静力学分析模型基础上,建立了球轴承的静力学平衡方程,即静力学模型。

虽然在高速重载工况下,采用静力学模型对球轴承刚度进行计算与分析,所得到的结果会与实际结果有较大的偏差;但是,无论如何,静力学模型为轴承的分析计算提供了一种新的思路。

在静力学平衡方程的基础上,邓四二[1]根据钢球与滚道的变形协调几何关系,推导出了轴承在负载条件下的轴向刚度和径向刚度;在非线性范围内,这些公式给出了负载与变形关系的表达式,同时也更好地对真实运动状态下的轴承进行了描述。JONES A B[2]提出了一种球轴承的滚道控制理论,并将其作为运动边界条件;同时,在对其进行计算的过程中充分考虑了摩擦的因素,丰富了轴承计算分析的方法。在此基础上,HARRIS T A[3]提出了一种五自由度球轴承刚度矩阵的计算方法,进一步奠定了轴承动力学分析的基础。

但是上述研究并未对球轴承的轴向自由度进行分析。同时,之前的文献[4-12]也只是对轴承刚度做了大量研究,而在研究过程中,对轴承刚度的外部影响因素考虑较少。

因此,笔者拟从球轴承的6个自由度方向对此进行分析计算,将球轴承与轴的变形分析相结合,在考虑轴受载变形的轴承-轴刚度模型的基础上,提出一种球轴承-轴的刚度进行计算方法;最后,将软件计算结果与文献对照数据进行对比,以验证所提出的计算方法能够对球轴承-轴的刚度进行计算。

1 轴承刚度计算与受载平衡

在球轴承中,滚动体与内外滚道的接触变形是影响滚动轴承运转精度和旋转稳定性的重要因素。通常情况下,需根据赫兹理论(Hertz-Theory)[13]对轴承接触应力进行计算。虽然Hertz的假设是点接触,但是赫兹弹性接触理论可以在一定程度上解决轴承接触应力与变形的问题。

Hertz点接触问题考虑的是两个任意弹性曲面在初始状态下仅一点发生接触的情况,所以,在分析轴承接触变形问题时要进行如下假设:

(1)接触体是线性弹性体,且均匀各向同性,在外力作用下只发生微小变形;

(2)接触体表面连续光滑,且接触形式仅属于局部接触;

(3)接触区长度远小于物体表面的曲率半径,忽略接触区附近物体的表面曲率;

(4)接触表面不存在摩擦力。

基于以上假设,笔者首先用二次函数来描述接触点附近的一般曲线方程;然后假定接触区是一个椭圆的形状,即接触应力呈半椭圆球函数分布;最后将弹性半空间的解引入接触区域内,以便对其进行法向位移的计算。

1.1 球轴承-钢球的几何变形关系

在径向载荷Fy、轴向载荷Fz和横向径向载荷Fx的共同作用下,球轴承分别产生竖直径向变形δy、轴向变形δz、横向径向变形δx;

在径向力矩载荷My、轴向力矩载荷Mz和横向径向载荷Mx的共同作用下,球轴承分别产生径向旋转位移βy、轴向旋转位移βz、横向径向旋转位移βx。其中,第i个滚动体的位置,用位置角φi表示。

球轴承的受力示意图如图1所示。

图1 轴承受力示意图

设轴承外圈与箱体固定,外圈不因载荷而产生变形,即外圈曲率中心Oo不变;第i个钢球受载前后,内圈曲率中心Oi和外圈曲率中心Oo之间的距离分别为A0和A(φi),则其变形可以表示为:

(1)

其中,A(φi)可由变形条件表示为:

(2)

(3)

式中:δri—第i个钢球受载后的径向变形;δzi—第i个钢球受载后的轴向变形;α0—钢球与滚道的初始接触角。

钢球的受载变形示意图如图2所示。

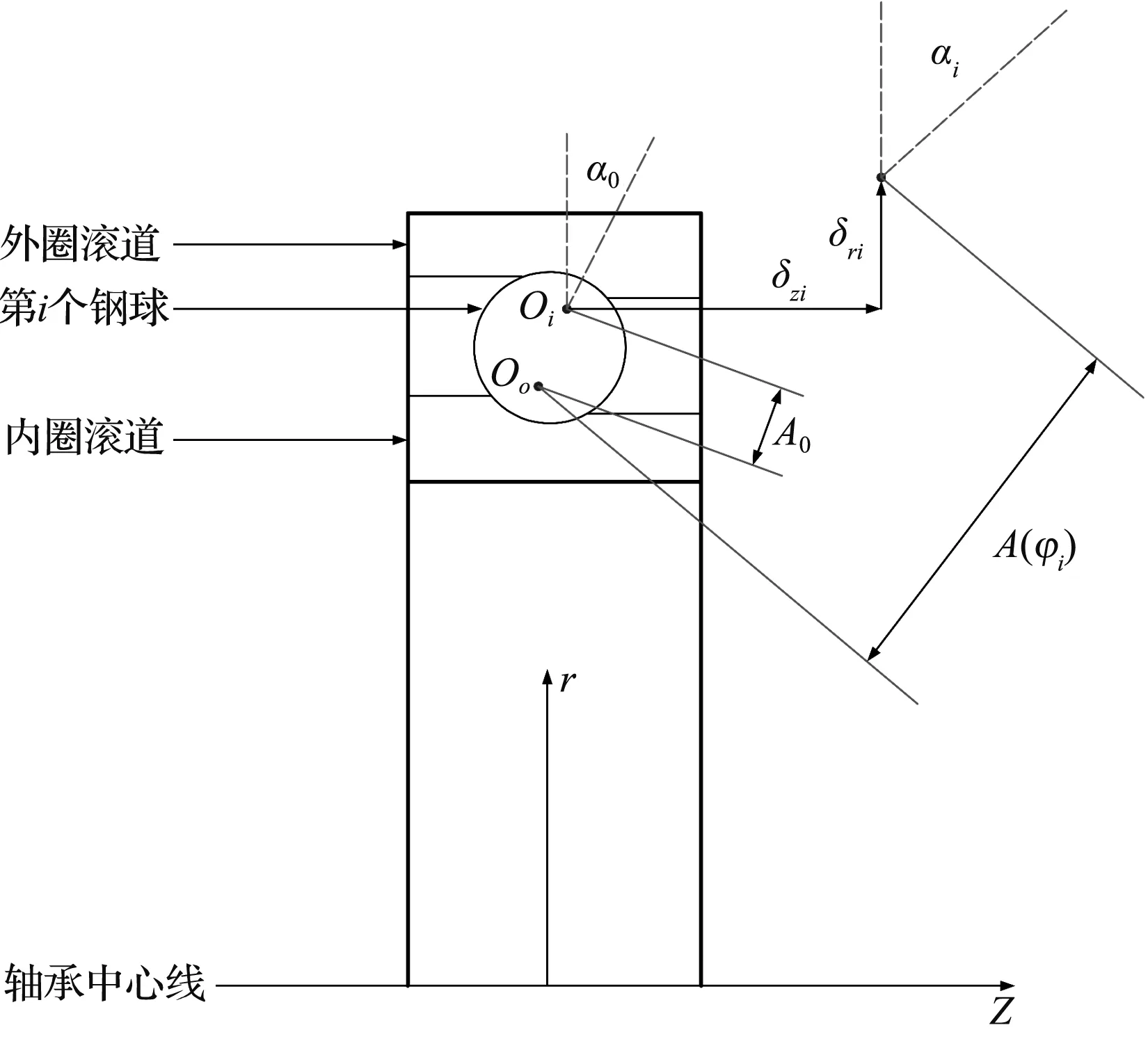
图2 钢球受力变形示意图

钢球受载变形和轴承坐标系下各自由度方向变形的协调关系,如图3所示。

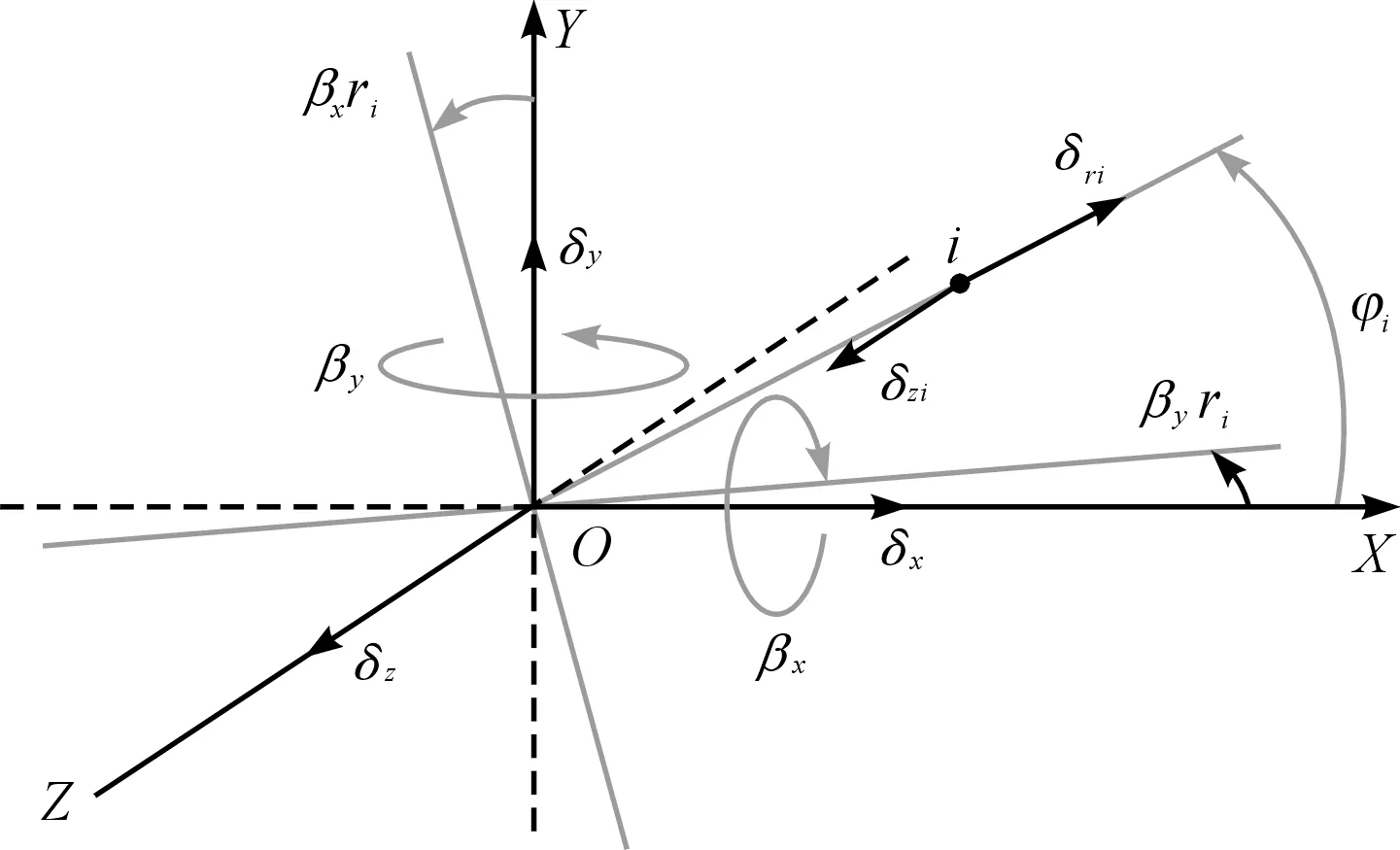
图3 钢球变形协调示意图

由图3可得:

(4)

式中:ri—内圈滚道曲率半径;rL—滚道与钢球的间隙。

1.2 球轴承的受载变形与刚度计算

在确定了轴承与钢球各方向上的变形位移关系后,还需要确定轴承与钢球各方向上的力平衡关系。

根据赫兹(Hertz)弹性接触理论,第i个钢球受载与变形的关系表达如下:

(5)

式中:Qi—轴承中第i个钢球与滚道局部接触点处的法向载荷;Kn—与接触材料、几何参数相关的参数。

当两弹性体的接触为线接触[14-18]时,n取10/9;当两弹性体的接触为点接触时,n取1.5。

笔者将每个不同位置、不同接触角、不同位置角的钢球的载荷与变形统一到轴承整体的坐标轴上,再通过对每个钢球的不同方向载荷的叠加,得到球轴承整体径向力载荷为Fym、轴向载荷Fzm、横向径向载荷Fxm、径向力矩载荷为Mym、轴向力矩载荷Mzm、横向径向力矩载荷Mxm,最终可得轴承的力与变形平衡方程:

(6)

式中:αi—第i个钢球受载变形后的接触角。

(7)

(8)

球轴承整体受到径向力载荷为Fym、轴向载荷Fzm、横向径向载荷Fxm、径向力矩载荷为Mym、轴向力矩载荷Mzm、横向径向力矩载荷Mxm,会分别产生δym、δzm、δxm、βym、βzm、βxm这6个方向的变形位移。

各个载荷分别对6个方向的位移求偏导,便可以得到轴承刚度的表达式,其矩阵形式如下:

(9)

值得注意的是,轴承刚度不是一个常量,它会随着位移(或载荷)的变化而变化,因此,在提到轴承刚度的时候,应该指出它与对应的位移或者载荷,否则就没有意义。

方程组很显然是一个非线性方程组。经过实测,该方程组选择使用牛顿-拉弗森(Newton-Raphson)[19,20]迭代效率最高。在编写雅各比矩阵的时候,最好将矩阵每一项写出,不建议使用编译器自带的函数求解雅各比矩阵。

假设在摆线齿锥齿轮传动系统中,轴承受到六自由度载荷Qb,此时的轴承刚度为Kb,那么可得此轴承受载变形平衡方程,以求解各自由度方向的变形δb,即:

(10)

至此,便得到了轴承刚度的表达与轴承受载变形平衡方程。以载荷作为输入参数进行方程求解,便可以得到六自由度变形和刚度矩阵。

1.3 滚动体接触相关参数的计算

当钢球载荷为Q时,其法向接触变形δr可以写为:

(11)

式中:G—柔度系数。

对于内、外滚道接触,公式如下:

(12)

钢球与两个滚道之间的法向趋近量如下:

δn=δi+δo=(Gi+Go)Q2/3

(13)

联立式(11～13),即有:

(14)

式中:E1，E2—接触材料的弹性模量;∑ρ1，∑ρ2—接触体的曲率和函数;Dw—钢球直径;fi—沟曲率半径系数;fo—外圈滚道沟曲率半径系数;dm—轴承节圆直径;α—初始接触角。

2 轴刚度计算与受载平衡

轴采用梁模型进行数学建模,对不同梁模型,目前有欧拉-伯努利(Euler-Bernoulli)梁模型和铁木辛柯(Timoshenko)梁模型。其中,铁木辛柯梁考虑了常剪应变,而欧拉梁则假定剪切刚度无限大,不发生剪应变。

具体而言,二者虽然都采用平截面假定,但对于变形前,垂直于中轴线的截面,欧拉模型在变形后仍保持与中轴线垂直;铁木辛柯梁模型则认为二者不再垂直,出现一个剪应变项。

从应用上看,若梁的跨径比大于5,梁通常是弯曲主控的,采用欧拉梁模型模拟;若跨径比小于5的梁,剪切变形明显,宜采用铁木辛柯梁。此处,笔者将采用欧拉-伯努利梁进行梁单元的建模。

笔者设轴为两节点梁单元,z方向表示梁单元的轴向,x和y表示梁单元的横向和纵向;A、B表示两个梁单元的两个节点位置,那么该梁单元的广义的坐标如下:

Us1={AB}T
A={xAyAzAθxAθyAθzA}
B={xByBzBθxBθyBθzB}

(15)

梁单元示意图如图4所示。

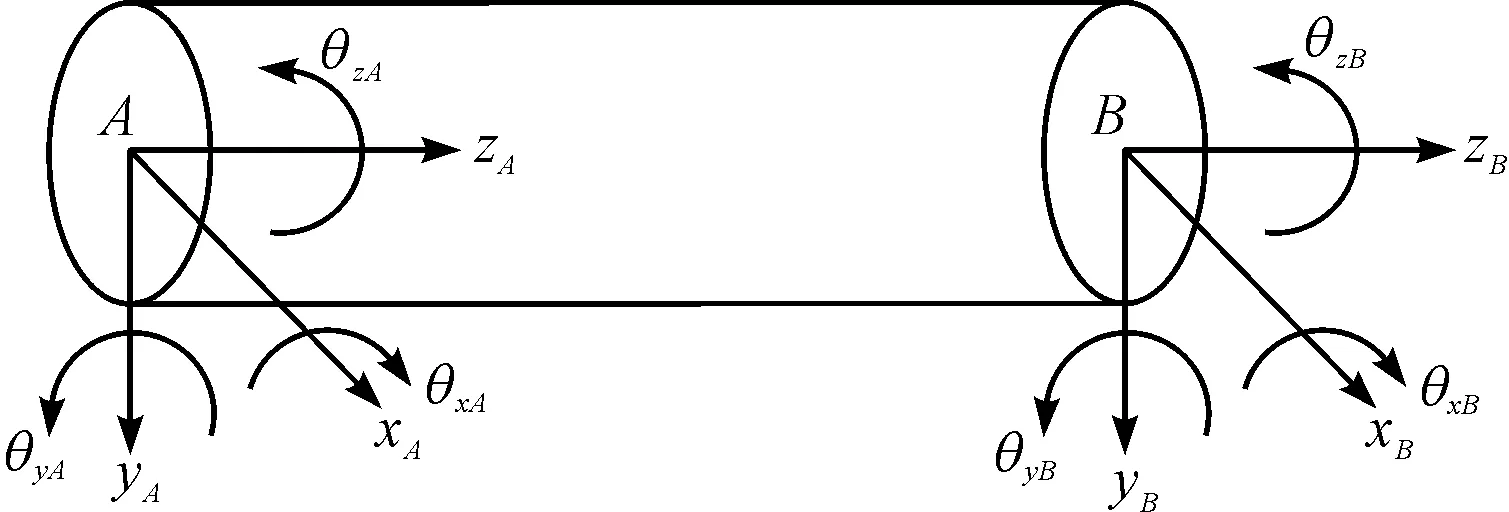
图4 梁单元示意图

根据材料力学理论,经典的Euler-Bernoulli梁单元的刚度矩阵如下:

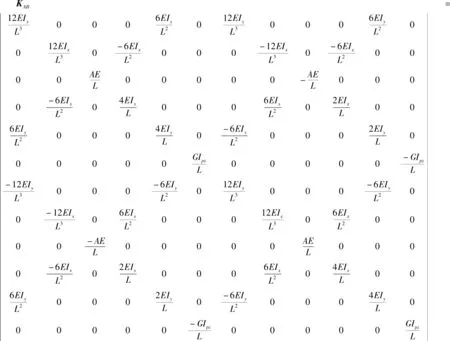
(16)

式中:E—弹性模量;G—剪切模量;A—梁的横截面积,mm2;Ix，Iy，Iz—轴x,y,z方向的惯性矩;Ipz—轴的极惯性矩。

变量具体表达如下:

(17)

式中:ν—材料的泊松比。

用此刚度矩阵便可以描述功率输入轴AB两节点梁单元的刚度。主对角线的12个元素分别由A节点6个主方向的刚度和B节点6个主方向的刚度组成。

设节点A处载荷QA和节点B处的载荷QB为:

(18)

将QA、QB作为主对角线元素,便可以得到载荷矩阵QAB:

QAB=

(19)

根据刚度的定义,即力与变形的关系,便可以得到在载荷QAB作用下,梁AB节点处广义坐标Us1下的变形为:

(20)

梁的受力平衡方程为:

FAB=KAB·δAB

(21)

通过求解该方程,便可以得到变形δAB。

3 轴承-轴系统受载变形

3.1 计算原理

根据结构力学的知识,可采用结构矩阵分析法对轴承-轴系统受载变形进行分析。结构矩阵分析的两种基本方法是矩阵位移法(刚度法)和矩阵力法(柔度法)。

矩阵位移法在计算中采用节点位移作为基本未知量,矩阵力法则采用多余力作为基本未知量。在结构矩阵分析法中,运用矩阵进行计算,不仅能使公式紧凑,形式上规格统一,而且便于计算过程程序化。因此,笔者在此处采用矩阵位移法进行分析。

在杆件结构的矩阵位移法中,把复杂的构件当作有限多个单元的集合,各单元彼此在节点处连接,从而形成整体。因此,笔者先把结构进行拆解形成有限多个单元节点,继而对各单元进行分析,建立单元的刚度方程用来描述力与变形的关系;再根据变形的协调条件,将离散的单元恢复为原构件系统,进而得到整体结构的刚度方程。通过这样一分一合的过程,就把复杂的结构计算问题转化为简单的单元分析与综合问题了。

因此,解决问题的方法分为两个大步骤:

(1)单元分析。研究单元的刚度矩阵;

(2)整体分析。考虑单元的集合,研究整体方程的组成原理和求解方法。

在梁单元材料[21,22]的力学性能和材料性能确定的前提下,当梁单元受到多个方向的力的作用时,由于梁单元受载变形具有独立性,便可以独立地计算梁单元多个方向上的受载变形。

一般情况下,梁单元的材料刚度为静刚度,即不会随着载荷的变化而变化。例如,对图5杆结构进行分析时,首先需要先将杆结构拆分成两个梁单元进行分析,得到梁单元①和梁单元②的刚度矩阵后,通过矩阵的定位叠加,最后得到梁整体的刚度矩阵,进而得到该结构的载荷与力。

3.2 分析与计算

根据前文可知,设轴拆分后的每个轴段的几何参数和材料参数相同,则每个轴段的刚度表达相同,且都能用欧拉-伯努利(Euler-Bernoulli)梁模型的刚度矩阵表达。

各单元耦合示意图如图5所示。

图5 单元耦合示意图

节点AB梁单元刚度矩阵可以简化为:

(22)

节点BC梁单元刚度矩阵可以简化为:

(23)

将节点AB梁单元刚度和节点BC梁单元刚度进行叠加耦合,轴的刚度矩阵可以重新表达为:

(24)

笔者把轴承1、轴承2安装在轴节点A、C位置,只要在轴上对应节点处进行刚度矩阵叠加即可。设轴承1与轴承2的刚度矩阵分别为Kb1、Kb2,矩阵大小均为6×6,表示每个自由度方向的位移。

由于轴承中心线与轴的中线重合,笔者通过坐标旋转将轴承坐标绕着z轴旋转η,使轴承的刚度表达坐标与轴坐标Us1一致;将轴承1的刚度和轴承2的刚度通过坐标变换矩阵转换到轴坐标系下,即:

(25)

M(ab)=|M11M12M13|

(26)

式中:M—坐标旋转矩阵,表示某矩阵绕着向量a旋转角度b。

(27)

(28)

(29)

(30)

设在坐标系Us1内,施加到轴上的载荷为Q,则轴承-轴模型受载变形可表达为:

(31)

(32)

式中:Q1，Q2，Q3—3个节点处的六自由度载荷。

轴承-轴受载变形的平衡方程为:

(33)

式中:δ1,δ2,δ3—轴上3个节点处的六自由度变形。

需要注意的是,如若涉及复杂空间几何,需将各个部件统一到同一坐标系下,再进行叠加耦合。

4 轴承实例验证

4.1 轴承刚度验证

笔者以代号6210的深沟球轴承为例,即接触角等于零的角接触球轴承,滚子直径为12.7 mm;轴承节圆直径为70 mm;滚子数量为10;内圈沟渠率系数为0.515;外圈沟渠率系数为0.515,选取其径向刚度进行对照验证;

再以代号7210B的角接触球轴承为例,即滚子直径为12.7 mm;轴承节圆直径为70 mm;滚子数量为15;内圈沟渠率系数为0.515;外圈沟渠率系数为0.525,选其轴向刚度进行对照验证。

轴承径向刚度对比结果如图6所示。

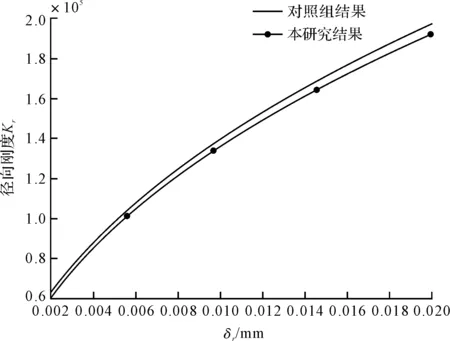
图6 轴承径向刚度对比结果

轴承轴向刚度对比结果如图7所示。

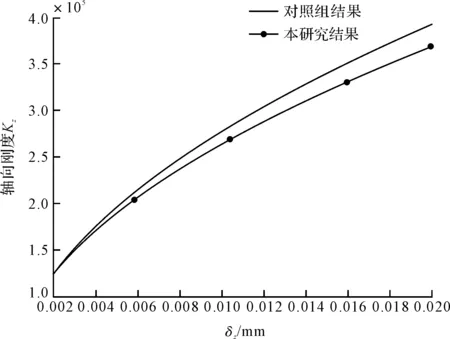
图7 轴承轴向刚度对比结果

图(6,7)中,笔者将上述计算结果与文献数据结果[23]进行了对比,结果表明,轴承径向刚度和轴向刚度的误差范围在7%～10%之间,均在可接受的范围之内。

4.2 轴刚度验证

笔者首先设置轴的参数,然后对其进行计算,再利用有限元软件对各个计算结果进行比对,结果显示,各结果之间完全一致。

轴的初始计算参数如表1所示。

表1 轴参数表

由于轴的刚度只与轴的几何参数和材料参数相关,笔者设节点距坐标原点的距离为dz,得到有限元输出的轴刚度,如表2所示。

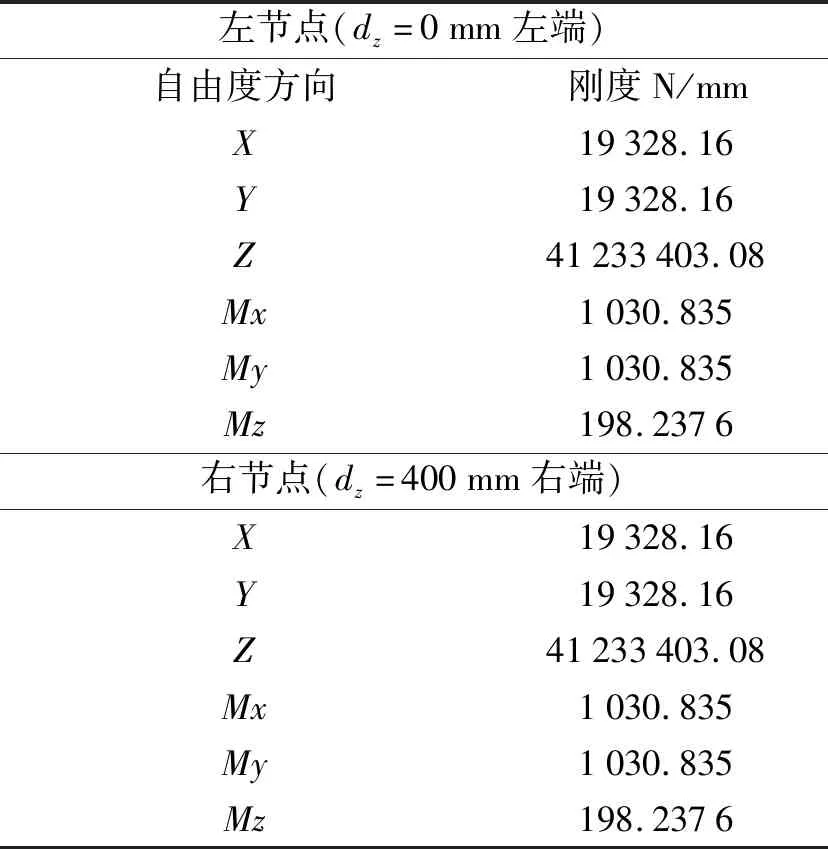
表2 有限元轴刚度输出表

以下矩阵为该节输出数据的1～6列:

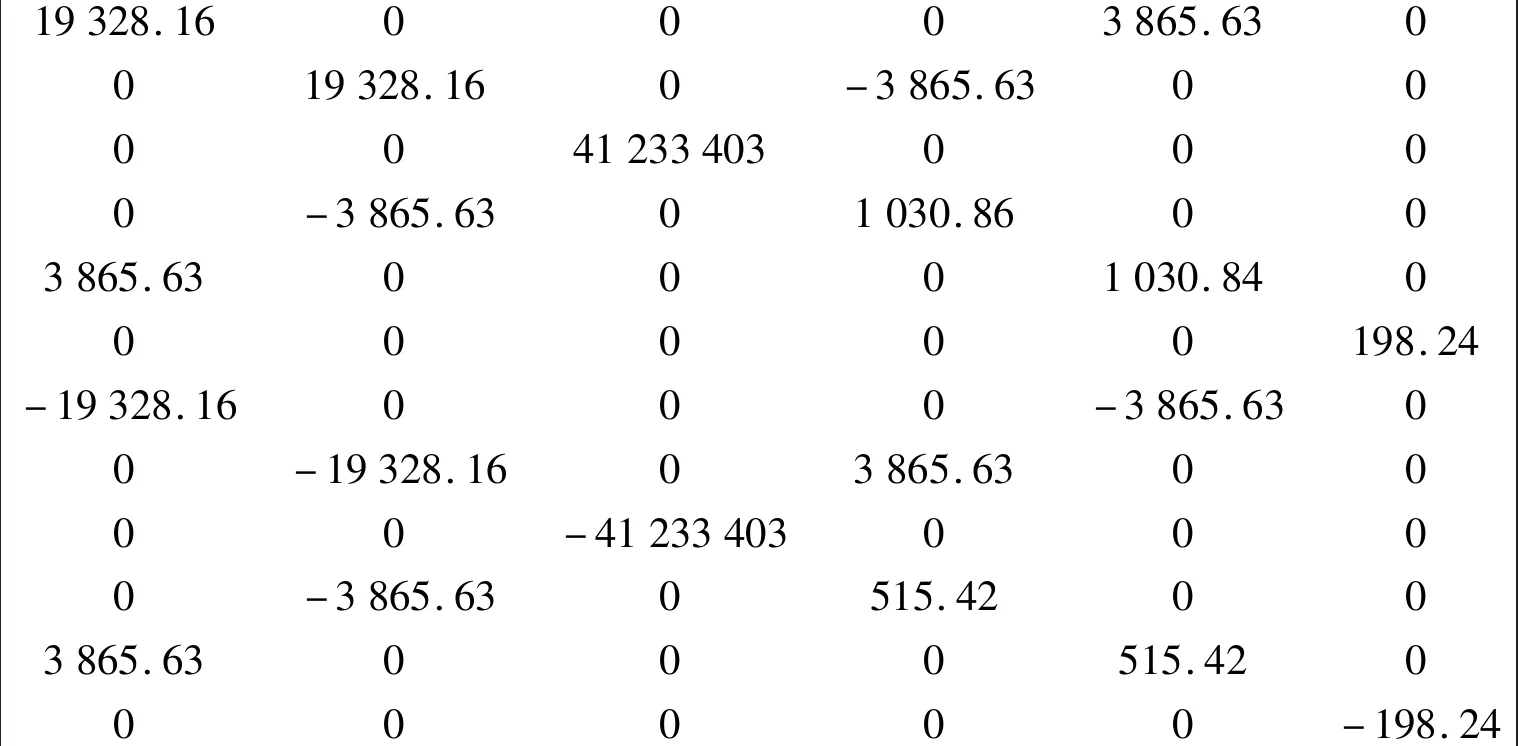
以下矩阵为该节输出数据的7～12列:

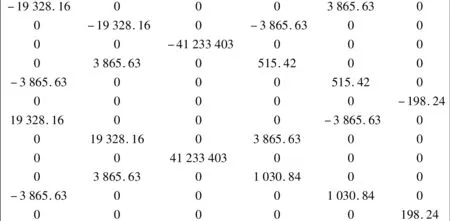
该节中使用的坐标系与有限元中的坐标系一致,矩阵中主对角线元素即轴上主方向上的刚度值,误差可忽略不计。

4.3 轴承-轴模型刚度验证

在上述各步骤分析的基础上,笔者进行轴承-轴模型系统的刚度耦合验证。

笔者在X方向输入载荷1 000 N,在Y方向输入载荷1 000 N,输入位置在轴的中点处;在同等条件下,输入载荷在X方向输入载荷1 500 N,在Y方向输入载荷1 500 N,载荷施加位置在轴中点处。

轴承-轴系统的分析模型如图8所示。

图8 轴承-轴分析模型

当X=1 000 N,Y=1 000 N时,模型各节点变形的计算结果与对照数据(文献数据)对比情况,如表3所示。

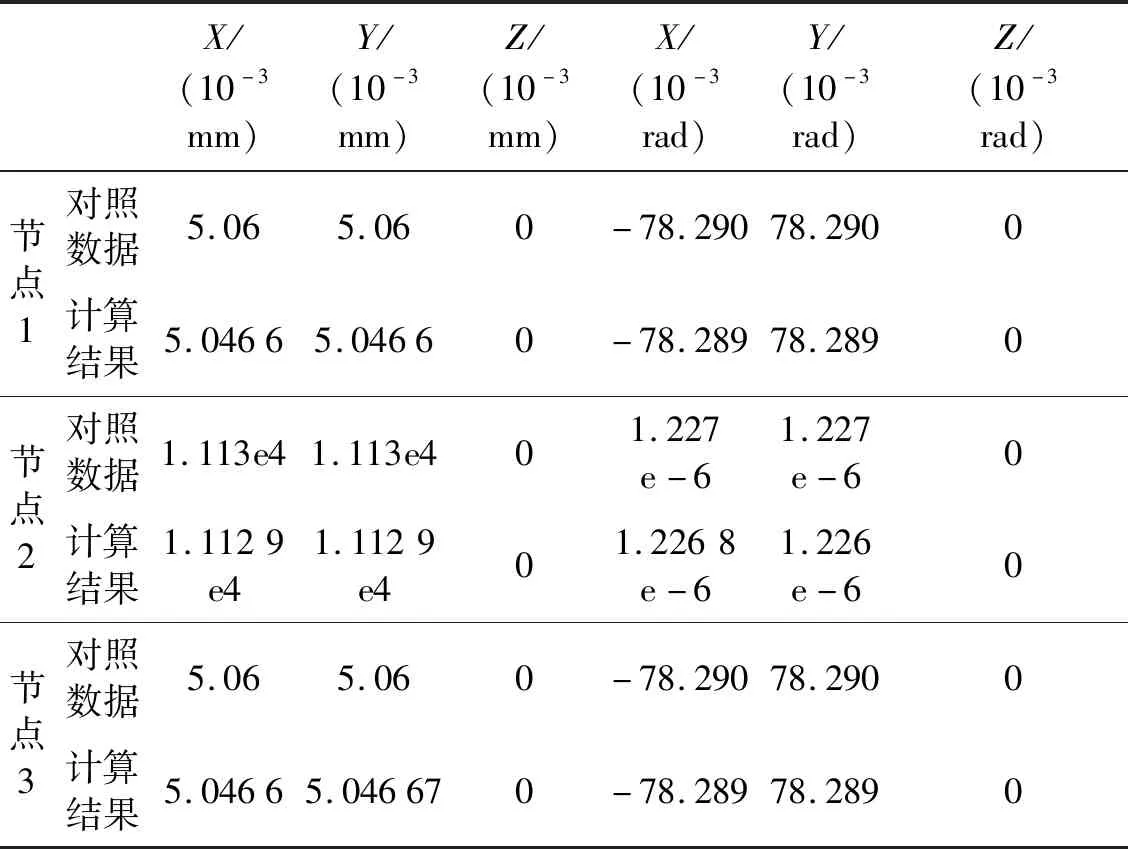
表3 模型各节点变形结果对照表

当X=1 500 N,Y=1 500 N时,模型各节点变形的计算结果与对照数据(文献数据)对比情况,如表4所示。

表4 模型各节点变形结果对照表

5 结束语

因为单一条件下球轴承的载荷-变形分析结果在理论和实际上存在偏差,并且以往研究者在分析球轴承时未考虑轴的受载变形影响,所以,笔者结合材料力学、结构力学、复杂杆件耦合以及变形协调与力平衡原则,构建了一种考虑轴受载变形的轴承-轴刚度模型,具体为:

基于赫兹接触理论以及变形协调与力平衡原则,构建了轴承刚度计算模型;基于欧拉梁模型,构建了轴刚度计算模型;基于材料力学与结构力学理论,构建了轴承-轴刚度耦合模型;

在此基础上,笔者实现了对轴与轴承的耦合分析,并将软件计算结果与文献对照数据进行了对比,验证了所提出的计算方法能够对球轴承-轴的刚度进行计算。

研究结论如下:

(1)在非重载条件下,轴承-轴刚度模型以及其计算方法是可行的,计算结果是准确的;

(2)在重载条件下,由于轴承刚度的计算数值存在一定误差,因此会影响模型计算结果的准确性;

(3)考虑了轴上点载荷对传动系统中轴-轴承的影响,为受载情况下轴承刚度的计算提供了一种方法。

在后续的研究过程中,为获得更加贴合实际的计算数据,笔者将在齿轮箱传动系统等非线性系统基础上,进一步考虑温度、变形、摩擦等因素对实验结果的影响,以期为传动系统的动力学分析提供理论基础。