基于广义除法下非线性模糊差分方程的动力学行为研究*
王贵英, 张千宏
1. 河池学院, 数理学院, 广西 河池 546300; 2. 贵州财经大学 数学统计学院, 贵阳 550025
模糊差分方程是指系数或初值为模糊数的差分方程, 模糊差分方程的出现, 解决了差分方程无法准确建模的问题, 因此, 模糊差分方程在许多科学研究领域有着举足轻重的地位.
针对于模糊差分方程的研究, 大多数学者更倾向于研究只具备模糊数乘法、 加法的模糊差分方程[1-5]. 文献[1]研究了一阶模糊差分方程
xn+1=ωxn+qn=0,1,2,…
其中:xn是模糊序列;ω,p,x0是正模糊数.
文献[2]研究了模糊差分方程
xn+1=Axn+Bn=0,1,2,…
正解的存在性、 有界性以及正解的渐近表现, 其中A,B,x0是正模糊数.
文献[6-12]研究带除法的模糊差分方程. 文献[6]通过对模糊数使用Zadeh扩展原则, 研究了模糊Riccati差分方程
正解存在性与唯一性等相关问题, 其中A,B,x0是正模糊数.
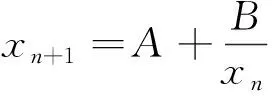
(1)
的全局渐近行为, 其中m∈N+,A,B以及初始条件x-m, …,x0都为正模糊数.
1 相关引理及定义

1)u是正规的, 即存在x为实数, 使得u(x)=1;
2)u是模糊凸的, 即对所有的t∈[0, 1],x1,x2∈R有
u(tx1+(1-t)x2)≥min{u(x1),u(x2)}
3)u是上半连续的;

对于所有的α∈(0, 1],u的α-截集表示为[u]α={x∈R:u(x)≥α}.
定义2[11]设u,v是正模糊数, 则u,v的α-截集表示为[u]α=[ul,α,ur,α], [v]α=[vl,α,vr,α],α∈(0, 1], 且
定义u的模为
u,v之间的距离为D(u,v), 其中

[g(u,v,ω)]α=g([u]α, [v]α, [ω]α)
定义3[11]令u,v是模糊数,α-截集为[u]α=[ul,α,ur,α], [v]α=[vl,α,vr,α], 0∉[v]α, 对于∀α∈(0, 1], 定义÷g(g-除法): 存在一个模糊数ω, 且[ω]α=[ωl,α,ωr,α], 使得
ω=u÷gv
即是
(2)
易知, 任意的模糊数u, 当u定义在g-除法上时, 有u÷gu=1, 当u定义在Zadeh扩展原则上时,u÷gu≠1.
引理2[11]令u,v都是模糊数, 如果ω=u÷gv存在, 则有以下两种情况.
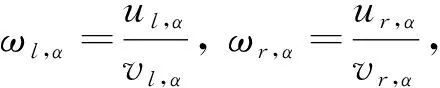
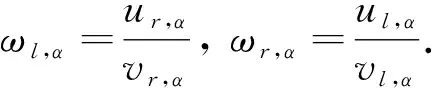
引理3[13]令u,v,ω都是正模糊数, ∀α∈(0, 1], 如果ω=u÷gv满足引理2中的1), 则
(3)
如果ω=u÷gv满足引理2中2), 则
(4)
因此有
(5)
注因为|ur,αvr,α-ul,αvl,α|≥|ur,αvl,α-ul,αvr,α|, 由(3),(4),(5)式可知, 运用g-除法优于Zadeh扩展原则.
引理4[13]考虑差分方程
(6)
其中:n=0,1,2,…,m;m∈N+,α,β,yi(i=-m,…,-1,0)都是正实数. 则
1) 方程
λ2-αλ-β=0
(7)
有一正一负的两个实特征根λ1,λ2.
定义4[11]令y=max{λ1,λ2}, 其中λi(i=1,2)是(7)式的特征根, 则称y为(6)式的唯一平衡点.
引理5[13]考虑差分方程系统
(8)
其中m为正整数,α,β,μ,ν,yi,zi(i=-m,…,-1,0)都是正实数. 则有
1) 方程
μλ2+(ν-αμ-β)λ-αν=0 (或αγ2+(β-μα-ν)γ-μβ=0)
(9)
有两个一正一负的实特征根λ1,λ2(或γ1,γ2).
2) 方程(9)的每一个正解, 都有
定义5[4]令y=max{λ1,λ2},z=max{γ1,γ2}, 其中λi,γi(i=1,2)是方程(9)的特征根, 则称(y,z)是方程(8)的唯一解.
定义6[4]设{xn}是正模糊数数列, 若存在正实数P,Q, 使得
supp(xn)⊂[P,Q]n=1,2,…
则称(xn)是有界且持久的.
定义7[11]如果正模糊数数列(xn)满足模糊差分方程(1), 则称xn是方程(1)的正解. 如果x满足方程
则称x是模糊差分方程(1)的平衡点.
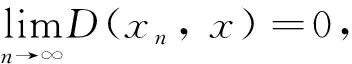
2 主要结论
主要对两个模糊数运用g-除法, 讨论高阶非线性模糊差分方程
(10)
解的唯一性以及全局渐进行为. 其中m为正整数,A,B,xi(i=-m,…,0)都是正模糊数.
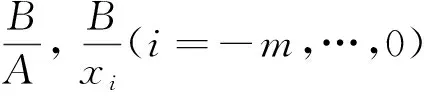
证定理的证明与文献[15]中的命题3.1的证明类似, 这里省略定理1的证明.
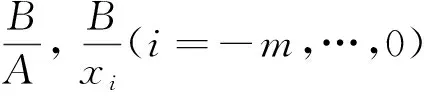
(11)
成立时, (10)式存在唯一解xn.
注定理2的证明方法与定理1基本一致.
定理3考虑差分方程(6), 存在一个正常数θ>0, 当n≥1时, 有
(12)
证由(6)式可知, 对于∀α≥1, 都有yn≥α. 当n→∞时, 则有
其中
所以有
同理可得
因此, 对于∀n≥m, 都有
yn≤θ
(13)
其中
由(6)式及(13)式, 可得
(14)
定理证明完毕.
定理4考虑方程(10), 其中A,B以及初始条件xi(i=-m,…,0)都是正模糊数, 当方程(10)中除法满足引理2中的1)时, 方程(10)的每一个正解xn都是有界持久的.
证因为A,B以及初始条件xi(i=-m,…,0)都是正模糊数, 所以存在Mi,Ni(i=0, 1, 2, 3, …,m)使得
(15)
令xn是方程(10)中满足引理2中1)情形时的正解, 由定理3及方程(10), 则有
(16)
其中
联系(15)式, 可得
由(15),(16)式可得到Ln,α≥P, 其中
同理得
因此, 对于n≥1, 有
也即是
由定义6知,xn是有界持久的. 证毕.
定理5考虑差分方程系统
(17)
其中m为正整数,α,β,μ,ν,yi,zi(i=-m, …, 0)都是正实数, 当不等式组
(18)
成立时, 存在正常数K1,K2,C1,C2, 使得
K1≤yn≤K2,C1≤zn≤C2
证由引理5可知, 系统(17)存在唯一正解(yn,zn), 且易得出yn≥α,zn≥μ, 当n→∞时, 由(17)式有
所以有
(19)
同理可得
(20)
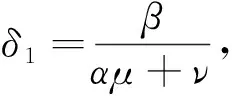
yn≤K2∀n≥1
(21)
其中

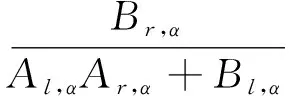
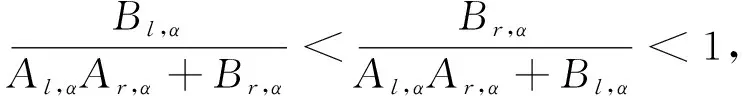
(22)
对于Ln,α,Rn,α, 由定理5以及(22)式有
其中
由(15)式有
再令
即P≤Ln,α, 同理可得Q≤Rn,α, 其中
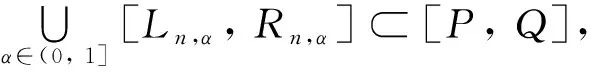
定理7当方程(10)中的g-除法满足引理2中1)时, 则
1) 方程(10)存在唯一平衡点x;
2) 当n→∞时, 方程(10)每一个正解xn都趋于唯一平衡点x.
证由引理2中1)与(10)式可得
(23)
(24)
由引理4、 (23)式和(24)式可知
(25)
由(15),(25)式有
(26)
(27)

并且
(28)
也即xn→x. 定理证毕.
定理8当方程(10)中的g-除法满足定理2中2)情形时, 则有以下结论成立
1) 方程(10)存在唯一平衡点x;
2) 方程(10)每一个正解xn都趋近于唯一平衡点x.
注定理8证明与定理7相似, 此处省略定理8的证明.
4 数值例子
例1考虑四阶模糊差分方程
(29)
其中:A,B以及初值xi(i=-3, -2, -1, 0)如下
取α-截集, 有
[A]α=[4+2α, 8-2α], [B]α=[5+5α, 15-5α], [x0]α=[6+2α, 10-2α]
[x-1]α=[2+α, 4-α], [x-2]α=[3+α, 5-α], [x-3]α=[4+α, 6-α],α∈(0, 1]

(30)
由定理4可知, 方程(29)的解都是有界持久的, 且存在唯一平衡点x, 当n→∞时, 方程(29)的每一个正解xn都收敛于唯一平衡点x(如图1-4).
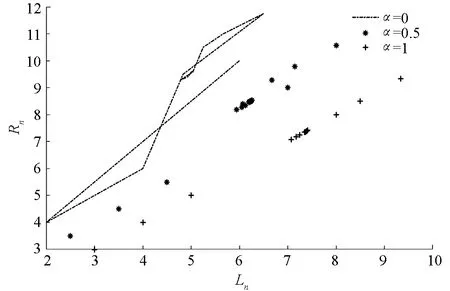
图1 系统(30)动力学行为
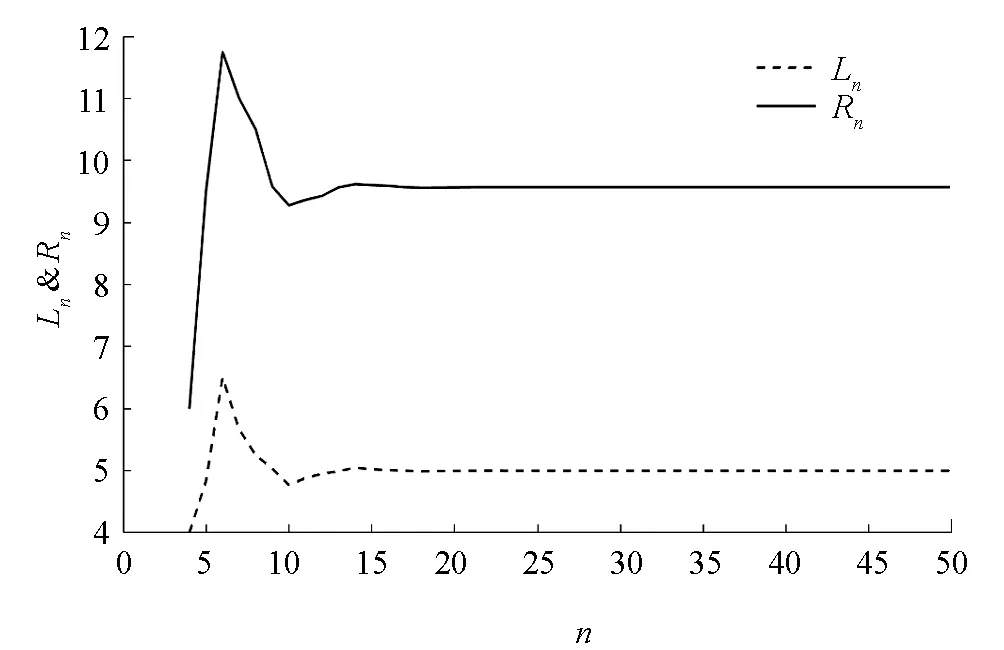
图2 α=0时, 系统(30)的解
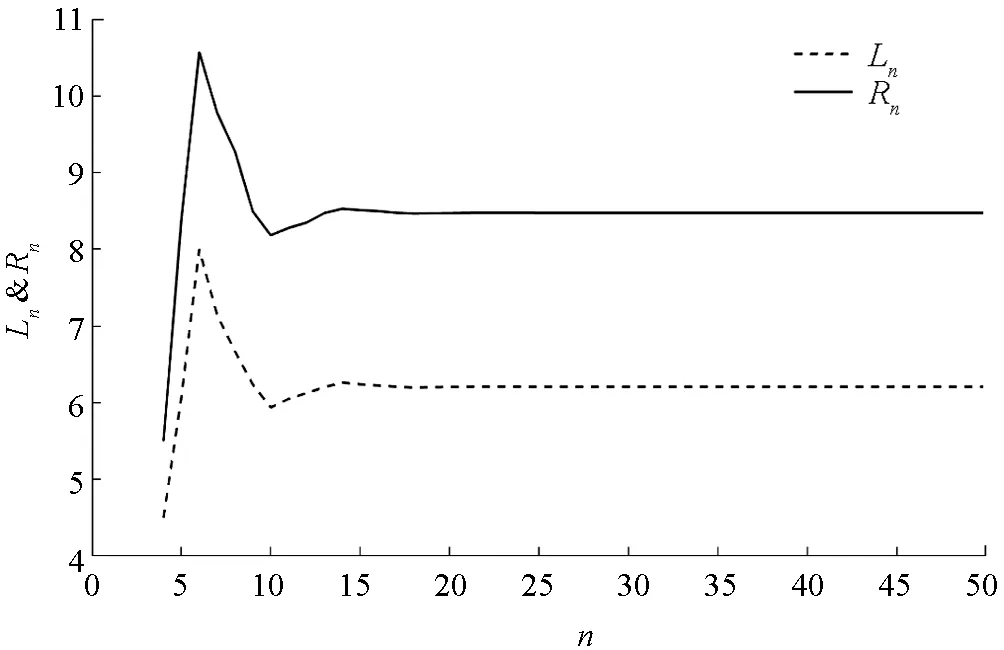
图3 α=0.5时, 系统(30)的解
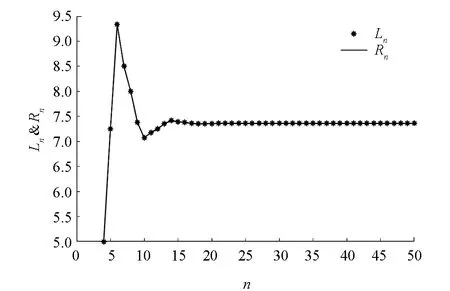
图4 α=1时, 系统(30)的解
例2考虑三阶模糊差分方程
(31)
其中A,B以及初值xi(i=-2, -1, 0)如下
所以有
[A]α=[1+α, 3-α], [B]α=[2+α, 4-α], [x0]α=[3+3α, 9-3α]
[x-1]α=[9+3α, 15-3α], [x-2]α=[15+3α, 21-3α],α∈(0, 1]
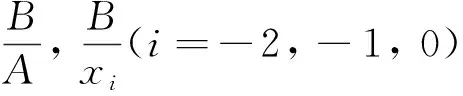
因此
(32)


图5 系统(32)的动力学行为
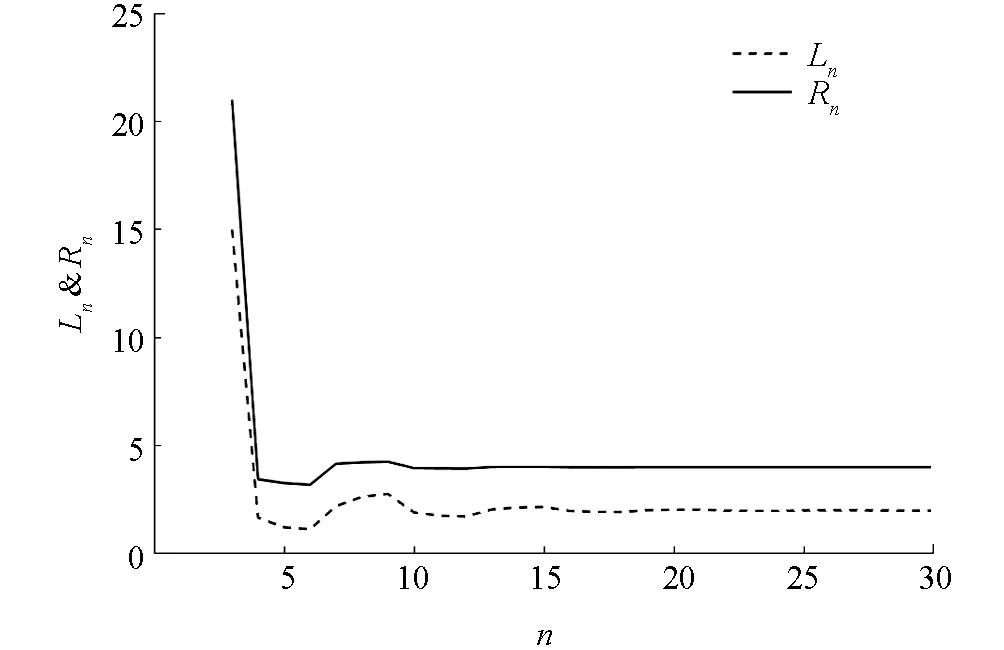
图6 α=0时, 系统(32)的解

图7 α=0.5时, 系统(32)的解

图8 α=1时, 系统(32)的解
5 总结
本文主要运用g-除法, 研究在两种情况下高阶非线性模糊差分方程(1)的正解存在性以及唯一性, 有界性以及持久性以及解的渐近行为. 结论得出, 方程(10)的每一个正解都趋近于唯一平衡点, 最后分别给出三阶和四阶符合条件的数值例子, 更好验证结论的有效性.

