二维多裂纹应力强度因子的辛离散有限元方法
丰艳霞,徐 旺,杨震霆,周震寰
(1. 大连理工大学 工程力学系,辽宁 大连 116024;2. 武汉科技大学 冶金工业过程系统科学湖北省重点实验室,湖北 武汉 430065)
0 引言
裂纹是工程结构中的主要缺陷形式之一,其失稳扩展将导致安全事故[1].在工程实际中,多裂纹情况更为常见,应力强度因子是定量评估裂纹是否稳定的重要依据,因此多裂纹应力强度因子(SIFs)的计算是断裂力学中的一个重要问题.
国内外学者已经在多裂纹问题的应力强度因子求解方面开展了大量研究.奇异积分方程法和复变函数法是常用的两类解析方法.基于奇异积分方程法,CHEN Y Z等[2]求解了有限尺寸板中多裂纹的SIFs.MONFARED M M等[3]分析了非均匀正交各向异性平面中多裂纹问题,并计算了对应的SIFs. HAGHIRI H等[4]求解了功能梯度正交各向异性半平面边界处多平行或垂直裂纹的SIFs.ZHAO J F等[5]计算了无限大板中多孔边裂纹的SIFs.解析方法虽然可以获得解析表达式,但是还受到无限域问题、简单边界条件等限制.为克服上述问题,大量数值方法被应用于多裂纹问题的求解,如有限元法(FEM)[6]、边界元法(BEM)[7]、无网格法[8].FEM虽然更简单,但是针对断裂问题的计算精度不高.BEM和无网格方法更精确,但是依赖于基本解,无网格方法的计算效率尚待解决.
基于解析辛方法[9-11]和FEM,提出一种适用于计算平面多裂纹问题的辛离散有限元方法(FEDSM).对含裂纹结构进行网格划分,并将其划分为裂纹尖端的奇应力区域和剩余的无奇异性区域.在近场内建立哈密顿系统,利用获得的辛本征函数进行节点未知量变换,得到FEDSM的计算列式,获得多裂纹对应的SIFs及其裂尖附近奇异物理场的解析表达式.
1 近场内哈密顿体系与解析解
1.1 问题的提出
整体含裂纹结构的区域划分见图1(a).为了方便表示,近场选取半径为RN的圆形.在近场内,选取极坐标(r,θ),r轴沿径向方向,原点位于裂纹尖端,对应的笛卡尔直角坐标为(x,y),ГFN为两类区域的分界线,见图1(b).
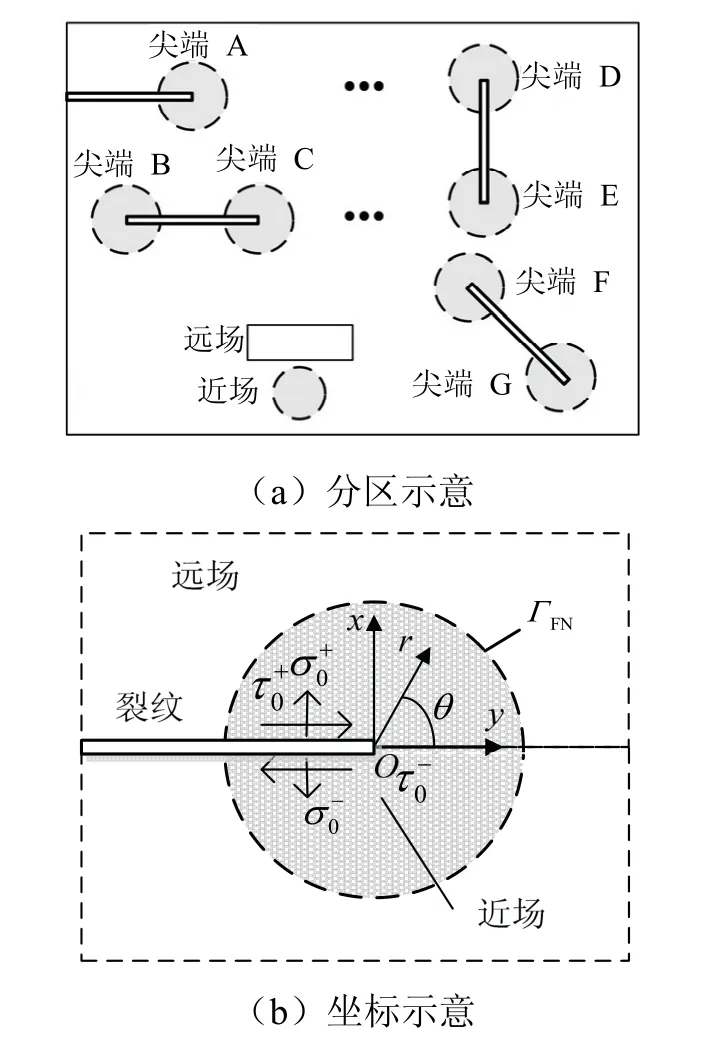
图1 多裂纹结构示意Fig.1 representation of multi-crack structure
1.2 近场内哈密顿控制方程
为在近场内建立哈密顿体系,定义广义坐标变量ξ,并定义变量对其导数为=∂f/∂ξ(f为任意变量).对于平面应力问题,哈密顿体系下的基本未知量[9]可以表示为
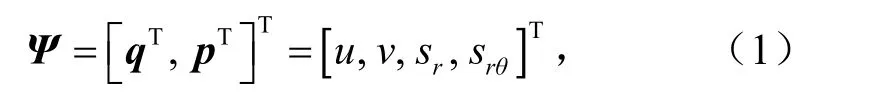
式中,q和p分别为原变量及其对偶变量向量,Pa·m;u和ν分别为径向和环向位移,m;sr和srθ为广义应力,N,其中sr=rσr和srθ=rτrθ;σr和τrθ分别为径向正应力和剪应力,N;r为极坐标半径,m;θ为极坐标旋转角度,°.忽略裂纹面载荷的影响,极坐标下平面应力问题的哈密顿控制方程可以表示为

式中,H为哈密顿算子矩阵;Ψ为哈密顿体系下的基本未知量.
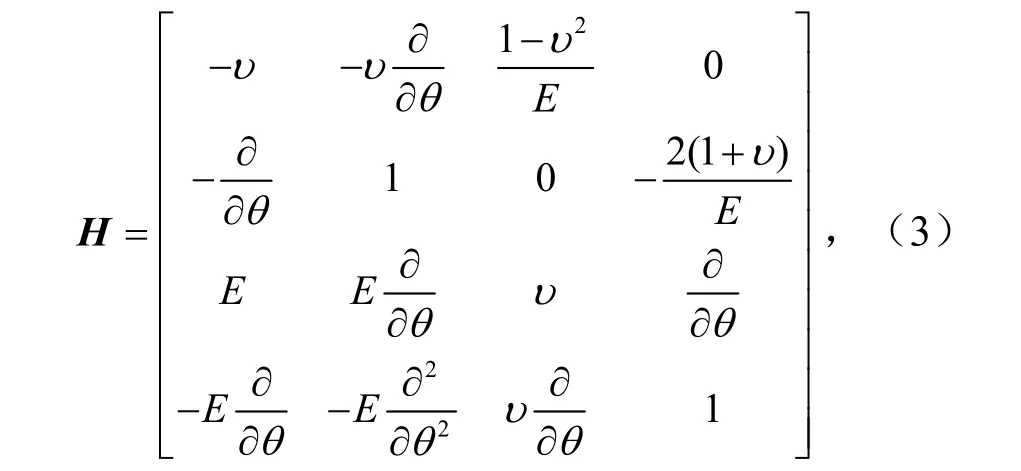
式中,E为弹性模量,Pa;υ为待定系数.
对应的裂纹表面边界条件为
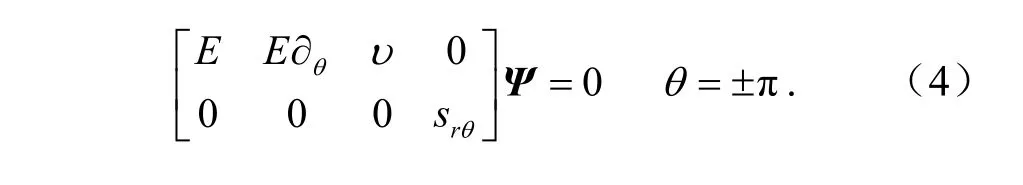
1.3 近场内解析解
在哈密顿体系下,哈密顿控制方程式(2)可以归结为哈密顿算子矩阵H的本征问题,即

式中,μ和Ψ为辛特征对.
式(2)的本征解可以分为两类[9].
① 零本征值本征解( 0μ= )为
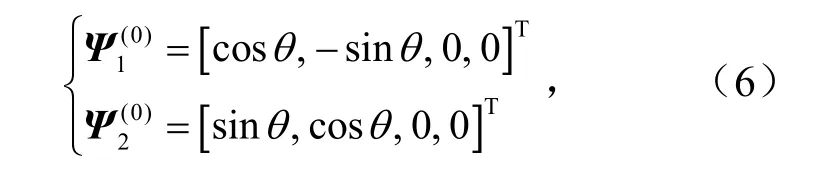
② 非零本征值本征解(μ=n/2,n= 1,2,3,…)为
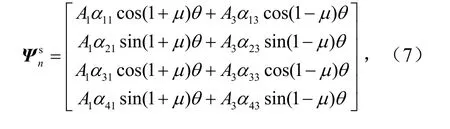
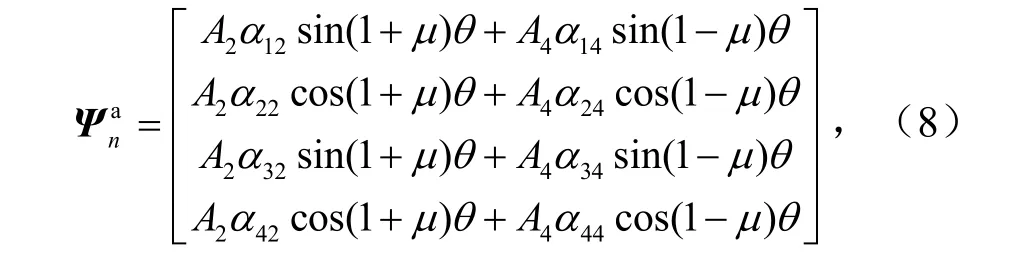
式中,上标s和a分别为对称和反对称本征解;A1~A4为待定系数.α11=α12=α13=α14=-α21=-α23=1,α12= -α24=(-3+υ-μ-υμ)/(3-υ-μ-υμ),α32=α34=Eμ(3-μ)/(3-υ-μ-υμ),α42=-α44=Eμ(1-μ)/,α31=α33=-α41=-α43=Eμ(1+υ).
由式(6)~式(8)可以表示式(2)的通解,其中位移函数可以表示为
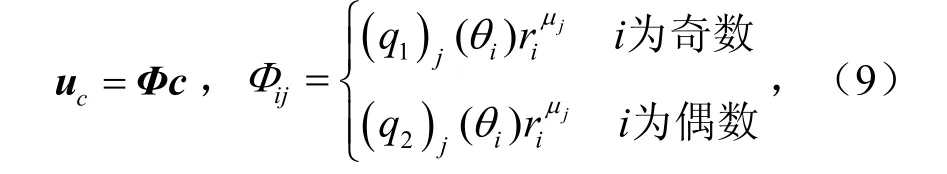
式中,uc为位移函数向量,m;q1为径向位移,m,q1=u;q2为环向位移,m,q2=v;ri为有限元节点坐标半径,m;θi为有限元节点坐标旋转角度,°;i为第i个节点,i= 1 -ZN(ZN为近场内节点数);j为第j阶辛本征解,j= 1 -ZM(ZM为选取的本征解项数);c为待定系数向量;Φ为变换矩阵.
2 辛离散有限元法
2.1 多裂纹结构的有限元列式
对于整体结构,其有限元列式可以表示为
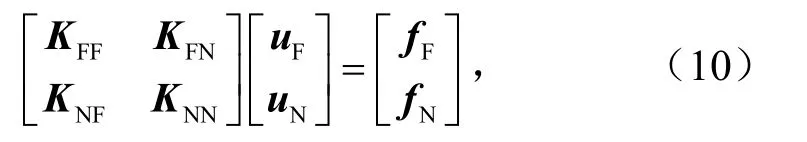
式中,u为节点位移向量,m;f为外力向量,N;K为有限元刚度矩阵;下标F和N分别代表远场和近场区域.
为了分析多裂纹问题,将整个裂纹体划分为几个子域,每个子域仅包含一个裂纹,见图2.
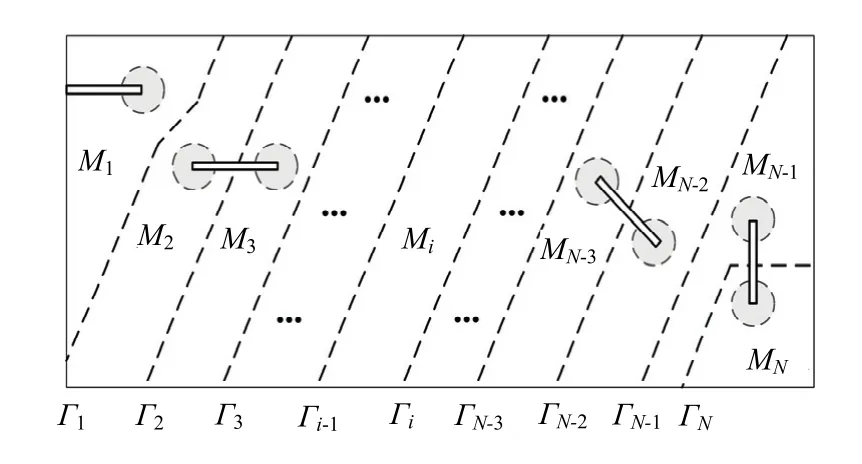
图2 子域划分示意Fig.2 signal of sub-domains divisions
图2 中Mi为第i个子域,Гi为相邻域分界线,i{1,2,∈ …,N}.各子域内的有限元列式如下.
第1个子域为
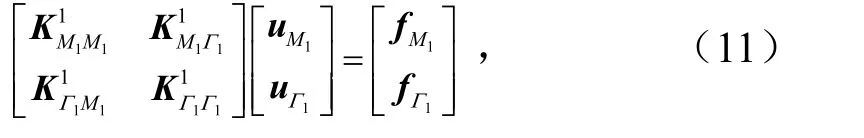
第i个子域为
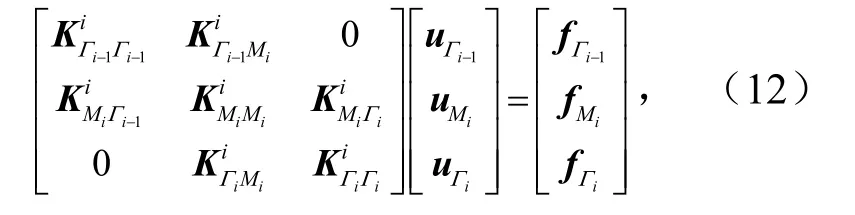
第N个子域为

由式(11)~式(13)可知,整体结构的有限元列式可以表示为

式中,

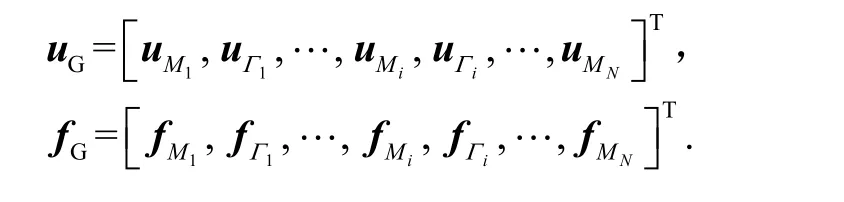
2.2 多裂纹结构FEDSM列式及应力强度因子
通过求解辛离散有限元列式(14),可获得问题在近场内的解析解为
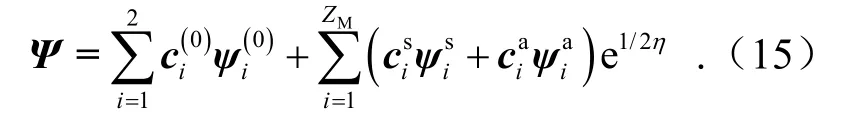
在近场内,广义应力的奇异项为
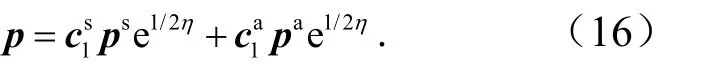
根据断裂力学定义,I型和II型SIFs为
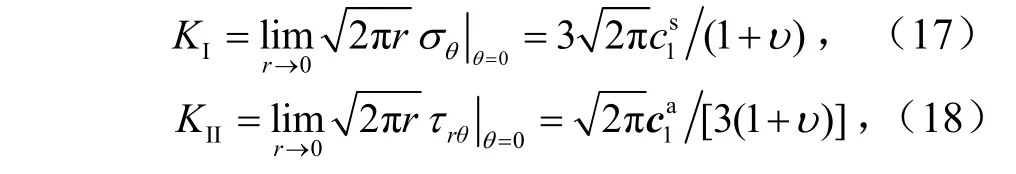
式中,KI为型应力强度因子;KII为型应力强度因子.
3 数值算例
数值算例将对工程中常见的I型和I、II混合型平面断裂问题展开研究,验证所提方法的正确性和精确性.
3.1 算例1
为验证所提出多裂纹问题FEDSM方法的准确性,选取含有一对变裂纹长度的弹性圆盘,见图3,圆盘半径为R,裂纹长度为a,在该圆盘外边界作用有沿径向向外的均匀应力σ.在计算中,选取ANSYS中的PLANE183单元对圆盘建模,近场半径RN= 0.1R,辛本征解取20 项.由于结构具有对称性,因此只需考虑其中一条裂纹的SIFs即可.图4为SIFs随裂纹长度的变化,FEDSM的计算结果与文献[12]的结果吻合良好,直接证明了所提方法是准确的.此外,为了说明近场尺寸的影响,取a/R为 0.5,图5为不同RN/R对应的SIFs随本征解展开项数的变化,当RN/R≥10%时,近场尺寸对计算结果已无影响.
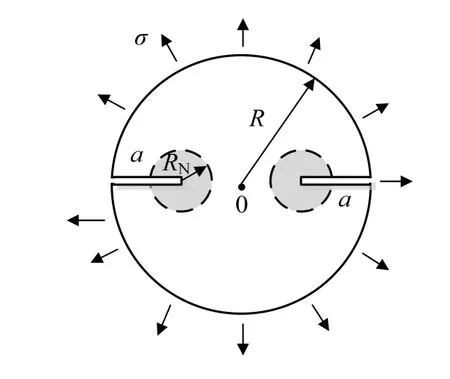
图3 含边裂纹圆盘Fig.3 edge-cracked circular disk
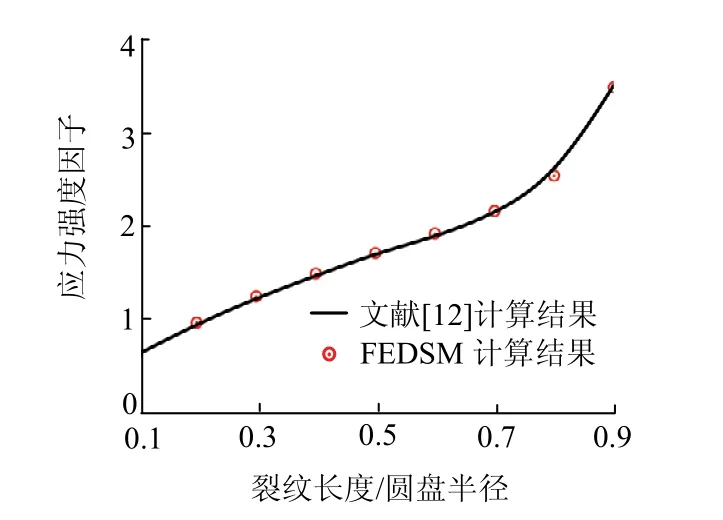
图4 SIFs随裂纹长度的变化Fig.4 variations of SIFs with crack length

图5 近场尺寸对应力强度因子的影响 Fig.5 effect of the Near field size on the stress strength factor
3.2 算例2
图6 为含有一对边裂纹的矩形板,矩形板尺寸为2h×2b,裂纹长度分别为a1和a2,上下两端受到均匀拉伸载荷作用σ.有限元单元类型、近场半径和本征解项数与算例1相同.算例中的SIFs数值均为无量纲数值,其中无量纲特征参数 0Kbσ= .
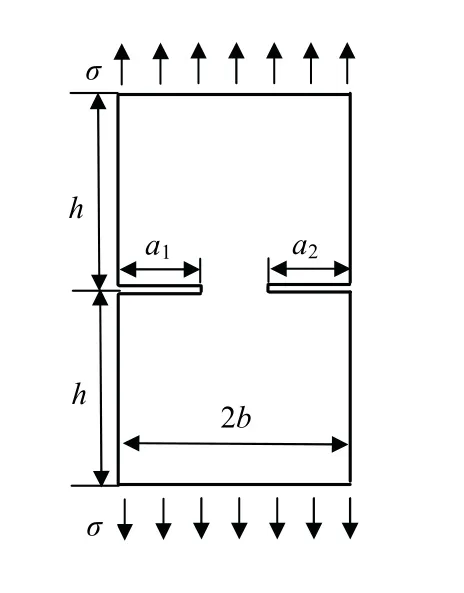
图6 含双裂纹矩形板Fig.6 rectangular plate with double edge-cracked
图7 为左端裂纹SIF随裂纹长度a1的变化.由图7可知,本计算结果与文献[13]结果一致,再一次证明所提出的FEDSM适用于多裂纹问题的SIFs求解.此外,图7表明非对称边裂纹的SIFs随裂纹长度的增加而逐渐增加.该现象表明整体结构和裂纹几何参数是影响多裂纹问题的重要影响因素.
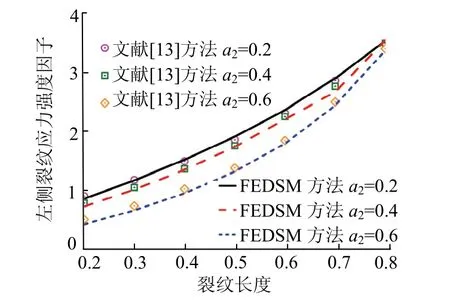
图7 非对称边裂纹SIFs随长度a2的变化Fig.7 variations of SIFs for non-symmetrical edge cracks with the crack length a2
3.3 算例3
算例3为较复杂的I、II混合型平面断裂问题.考虑含有1对共线斜裂纹的矩形板,其几何参数见图8,长宽比h/b为2,裂纹长度均为a.有限元单元类型、近场半径、本征解项数和无量纲特征参数与算例2相同.
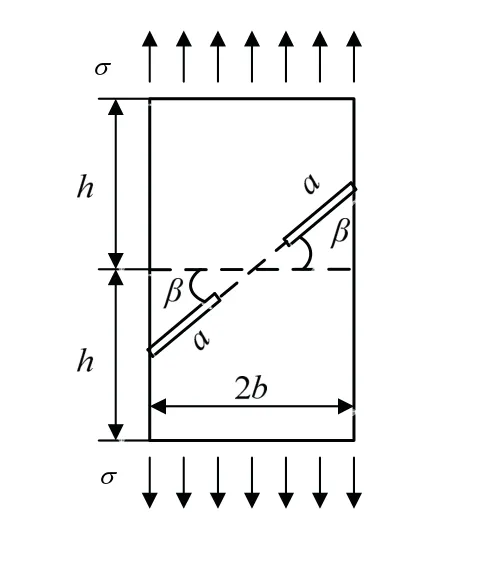
图8 含双斜裂纹的矩形板Fig.8 rectangular plate with two inclined cracks
表1和表2分别列出了不同裂纹角度和长度对应的I型和II型SIFs.为验证本计算结果的正确性,表格中同时给出了ANSYS的计算结果,选用单元类型与FEDSM相同,并且裂纹尖端单元采用1/4节点单元.从表1和表2中的数据可以看出,FEDSM和ANSYS获得的I型和II型SIFs数据结果一致.I型和II型SIFs都随裂纹长度的增加而增加;随着裂纹角β的增加,I型SIFs减小,而II型SIFs继续增大.该现象与算例2类似,表明裂纹几何参数是影响其SIFs数值的重要因素.
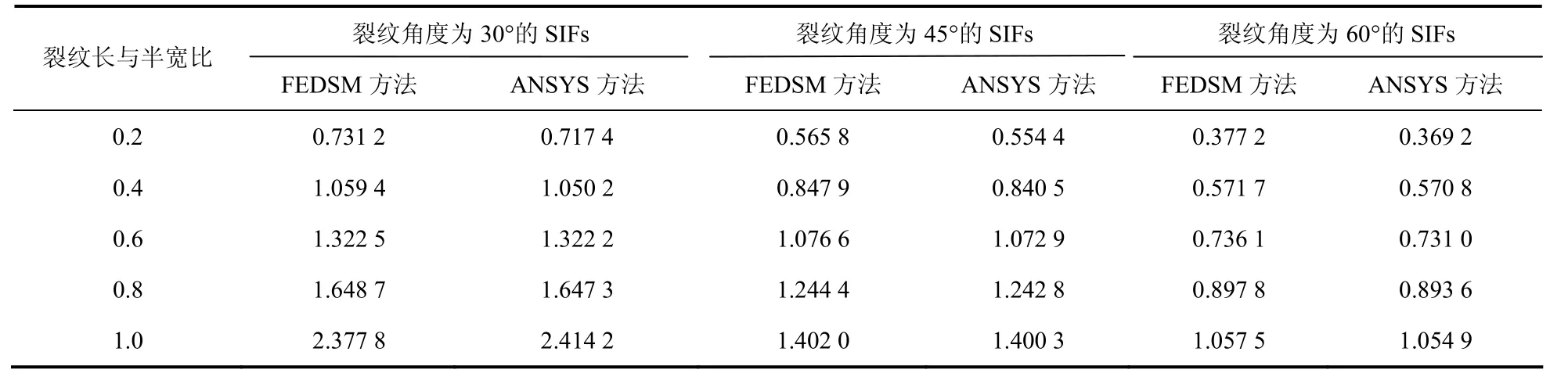
表1 不同裂纹角度和长度双斜裂纹的无量纲I型SIFs(h/b = 2)Tab.1 normalized mode I SIFs of two inclined cracks for various crack angles and lengths (h/b = 2)
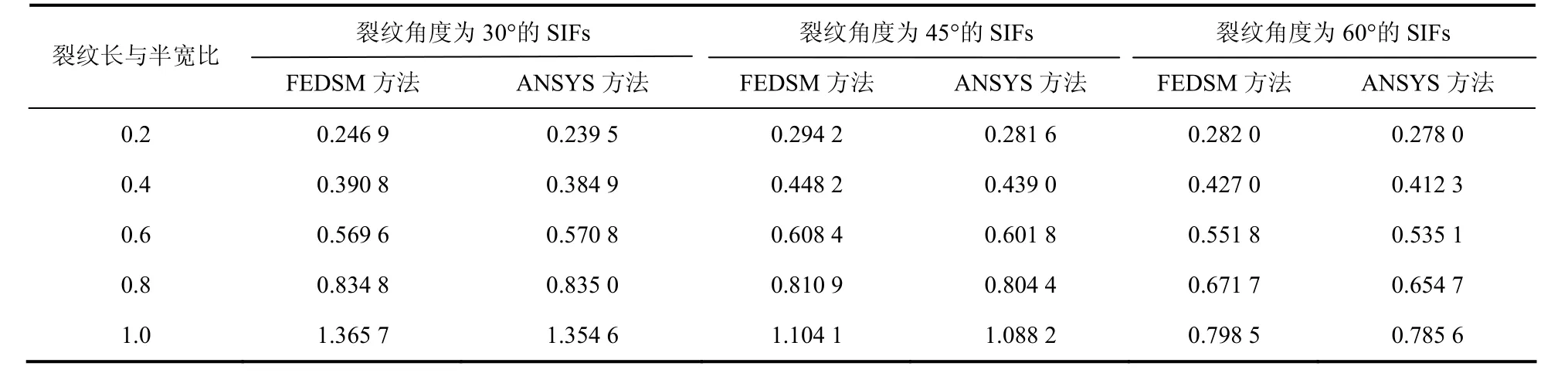
表2 不同裂纹角度和长度双斜裂纹的无量纲II型SIFs(h/b = 2)Tab.2 normalized mode II SIFs of two inclined cracks for various crack angles and lengths (h/b = 2)
除SIFs外,裂纹尖端附近的奇异应力场分布也是结构断裂分析的关键.选取在裂纹尖端周围的长和宽为l1=l2= 0.1b的正方形路径,见图9(a),对应的奇异应力变化规律见图9(b)~图9(d),所获应力分量与FEM结果非常吻合.
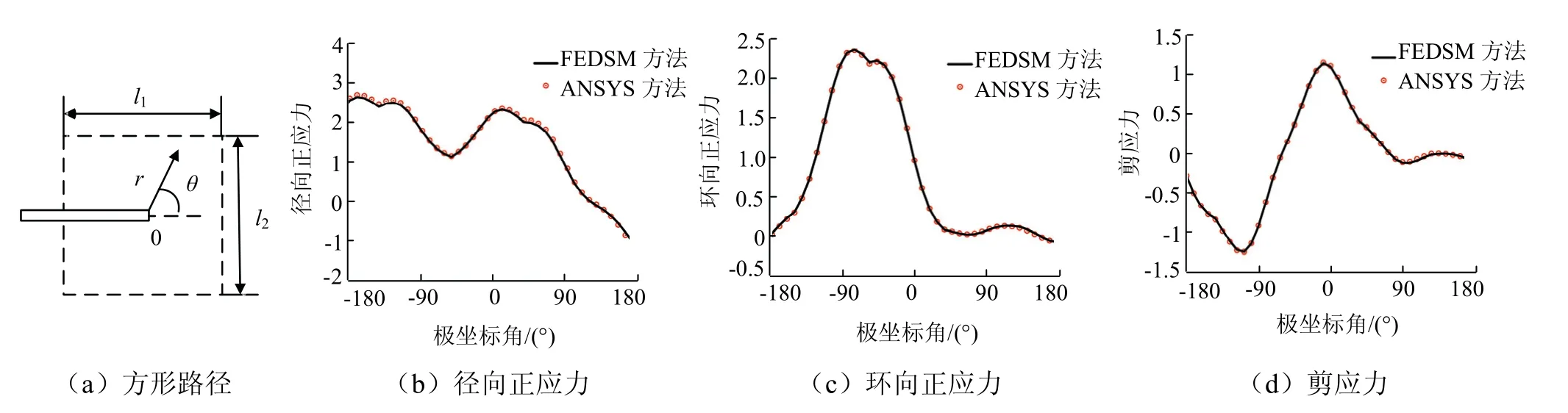
图9 沿正方形路径l1 = l2 =0.1b的无量纲应力分量Fig.9 dimensionless stress components along the square path with l1=l2=0.1b
4 结论
提出一种适用于多裂纹结构应力强度因子计算的辛离散有限元方法.该方法通过将整体结构划分为多个子域实现多裂纹问题简化,并在各个子域内将解析辛方法与传统有限元方法相结合,直接获得应力强度因子和该区域内物理场的解析表达式.与其他数值方法相比,辛离散有限元方法具有3个优势:① 通过在近场内进行未知变量变换,将未知量的数量大幅降低,直接减少断裂分析的计算时间和计算机的存储需求.② 该方法无需引入新的特殊单元,并且无需后处理程序即可求解SIFs.③ 该方法可以直接获得近场中的位移和应力的解析解.

