多目标区间值优化问题的最优性条件*
黄晓美,唐国吉
(广西民族大学数学与物理学院,广西南宁 530006)
0 引言
随着不确定在实际工程优化频繁呈现,作为一类含区间参数的优化问题引起了研究者的关注。最优性条件对于求解区间值优化问题尤为重要。近年来,一些学者对区间值优化问题解的最优性条件展开研究。文献[1-2]获得含不等式约束的单目标可微的区间值优化问题的KKT条件和对偶理论。文献[3-4]分别通过函数伪不变凸,拟不变凸和预不变凸,不变凸的性质获得单目标可微区间值优化问题的KKT充分性条件及对偶理论。文献[5]利用Clarke次微分获得单目标非光滑区间值优化问题的Fritz-John和KKT最优性条件。文献[6]把实值的多目标优化问题的Pareto最优解的概念推广到多目标区间值优化问题,并在目标函数和约束函数都是可微且凸的条件下得到KKT充分性条件。文献[7]在凸性条件下研究向量值的区间优化问题与向量变分不等式之间的关系。文献[8]利用Clarke次微分得到含不等式约束的多目标区间优化问题的Fritz-John和KKT最优性条件。
广义Jacobi矩阵是由Clarke针对向量值函数引入,[9]文献[10]考虑优化问题的所有函数为区间值函数,通过广义Jacobi矩阵,获得另一种形式的Fritz-John和KKT最优性条件,并解释了对于相同的乘子,通过广义Jacobi矩阵获得的最优性条件的解集包含于Clarke次微分型的最优性条件的解集,反之不成立。这说明了满足广义Jacobi矩阵型的最优性条件的乘子集合范围更小。受文献[10]的启发,本文主要工作是把文献[10]的结果推广到多目标区间值优化问题,获得局部LU-有效解的最优性条件。
1 预备知识
我们用I^表示实数集R上所有闭区间的集族。设A是I^上的任意一个闭区间,记为A=[aL,aU],其中aL和aU分别表示闭区间A的下界和上界,易知aL≤aU。若aL=aU=a,则A=[aL,aU]=a是一个实数。
定 义 1[1]称 F:Rn→I^ 为 闭 区 间 值 函 数 ,如 果 对 任 意 的 x∈Rn,F(x)均 为 R 上 的 闭 区 间 ,记 F(x)=[ FL(x),FU(x)],其中FL和FU称为F的左右端点函数,且FL和FU是定义在Rn上的实值函数,并且对任意的x∈Rn满足FL(x)≤ FU(x)。
定义2[1]设A=[aL,aU]和B=[bL,bU]是I^上任意两个闭区间,定义如下运算:
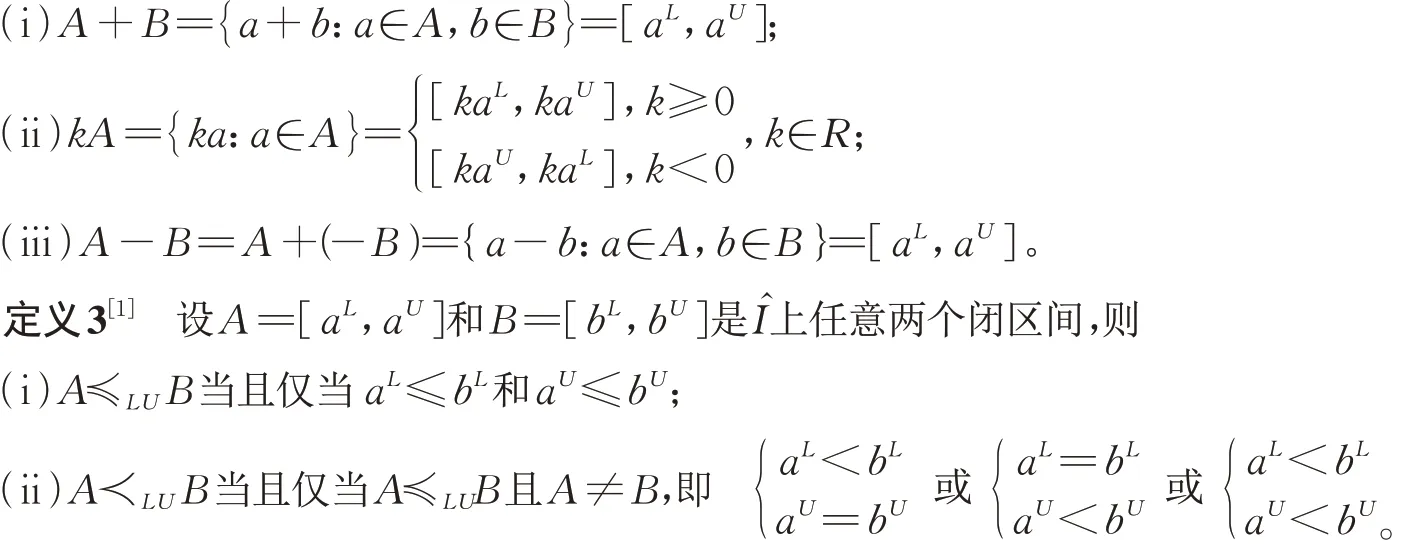
用Λm×n表m行n的矩阵空间,|||·|||为Λm×n上的范数,则任意的矩阵A∈Λm×n有|||A|||=max|aij|,其中A=(aij),1≤i≤m和1≤j≤n,记Aj为A的列向量。下面回顾向量值函数次微分的概念。
定义4[9]设T⊂Rn为非空开子集,f=( f1,…,fm):T→Rm是局部Lipschitz连续的向量值函数,则f在x0∈T处的广义Jacobi矩阵为

其中集合Tf表示f在T中不可微点的全体,J( f,xi)为f在xi处的Jacobi矩阵,co表示凸包。
从文[9]可知,关于广义Jacobi矩阵有如下性质:
(i)℘( f,x0)是非空紧凸集;
(ii)集值映射 x ⇉℘( f,x)是局部有界的,即存在关于 x0的邻域 V 和常数 K 使得对所有的 x∈V 有 max {|||A|||:A∈℘( f,x)}≤K;
(iii)℘( f,·)是上半连续的集值映射,因此对于x→x0,An→A0且An∈℘( f,xn),则A0∈℘( f,x0);
(iv)℘T( f,x0)⊂(∂f1(x0),…,∂fm(x0)),即任意矩阵A∈℘T( f,x0),有Ai∈∂fi(x0),i=1,…,m。
引理1[10]设T⊂Rn是非空开子集,f=( f1,…,fm):T→Rm是局部Lipschitz连续的向量值函数,φ:Rm→R是连续可微的实值函数,则
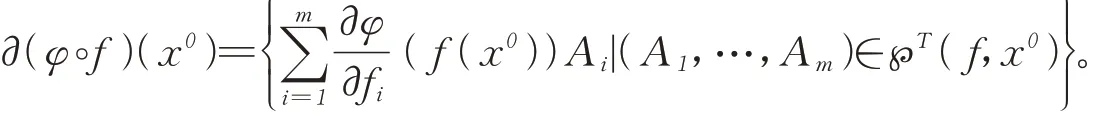
定义5[8]设x=(x1,…,xn)T和y=(y1,…,yn)T是Rn上的任意向量,定义如下:
(i)x=y当且仅当xi=yi,对所有的i=1,…,n;
(ii)x ≧ y当且仅当xi≥yi,对所有的i=1,…,n;
(iii)x≥y当且仅当x ≧y且x≠y;
(iv)x>y当且仅当xi>yi,对所有的i=1,…,n;
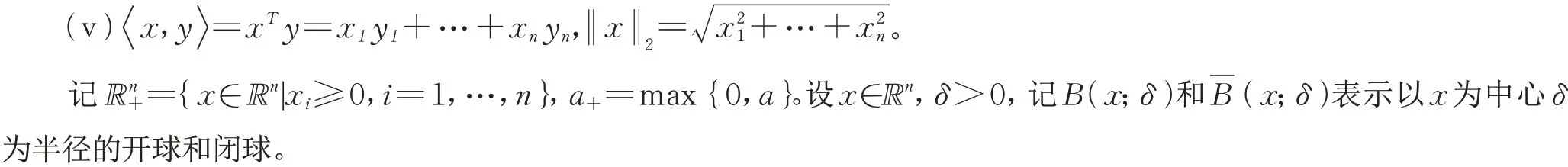
引理2[12]设φ:Rn→R是局部Lipschitz连续。如果φ在点x处达到极值,则0∈∂φ(x)。
引理 3[12](i)若 φ:Rn→R 是连续可微函数,则对任意的 x∈Rn,φ 在点 x 处是局部 Lipschitz 连续,且 ∂φ(x)={∇φ(x)};
(ii)若φ:Rn→R是凸函数,则对任意的x∈Rn,φ在点x处是局部Lipschitz连续;

(iv)设 φi:Rn→R(i=1,…,m)是均为局部 Lipschitz 连续函数,定义函数 φ:Rn→R 为 φ(x)=max {φi(x)|i=1,…,m },则 φ 是局部 Lipschitz 连续函数,且对任意的 x∈Rn均有 ∂φ(x)=co{∂φi(x)|i∈T(x)},其中 T(x):={i∈{1,…,m }|φi(x)=φ(x)};
(v)若φ:Rn→R是局部Lipschitz连续函数,则φ2也是局部Lipschitz连续函数。
2 Fritz-John和KKT最优性条件
本文主要考虑如下区间值优化问题:
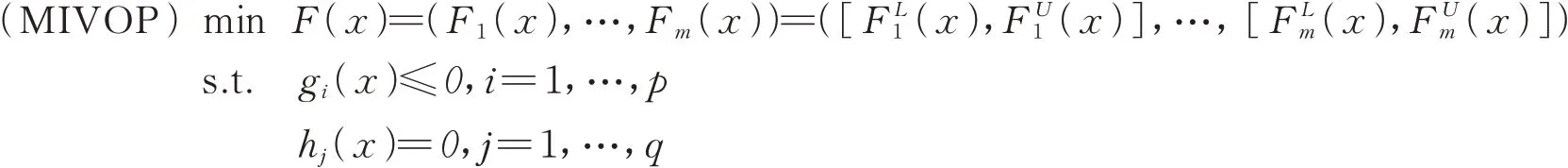
其中FLℓ,FUℓ:Rn→R(ℓ=1,…,m),g:Rn→Rp和h:Rn→Rq是局部Lipschitz连续函数。令Ω:={ x∈Rn|gi(x)≤0,i=1,…,p;hj(x)=0,j=1,…,q}为可行集,I(x0):={i|gi(x0)=0,i=1,…,p}为有效约束函数的指标集。为了方便,记M={1,…,m },P={1,…,p},Q={1,…,q}。
定义6 称可行点x0是问题(MIVOP)的局部弱LU-有效解,如果存在实数δ>0使得不存在x∈Ω∩-B(x0,δ),对任意的ℓ∈M满足Fℓ(x)≺LUFℓ(x0)。
注1:(i)若区间值函数Fℓ(x)(ℓ∈M )的左右端点函数相等,则问题(MIVOP)退化为实值多目标优化问题。故局部弱LU-有效解退化为局部弱Pareto-有效解。
(ii)当-B(x0,δ)=Rn,定义6的局部弱LU-有效解是弱LU-有效解,即文献[6]定义的多目标区间值优化问题的第一型弱Pareto最优解。
下面例子说明局部弱LU-有效解非空。
例1 设x∈R,考虑如下问题:
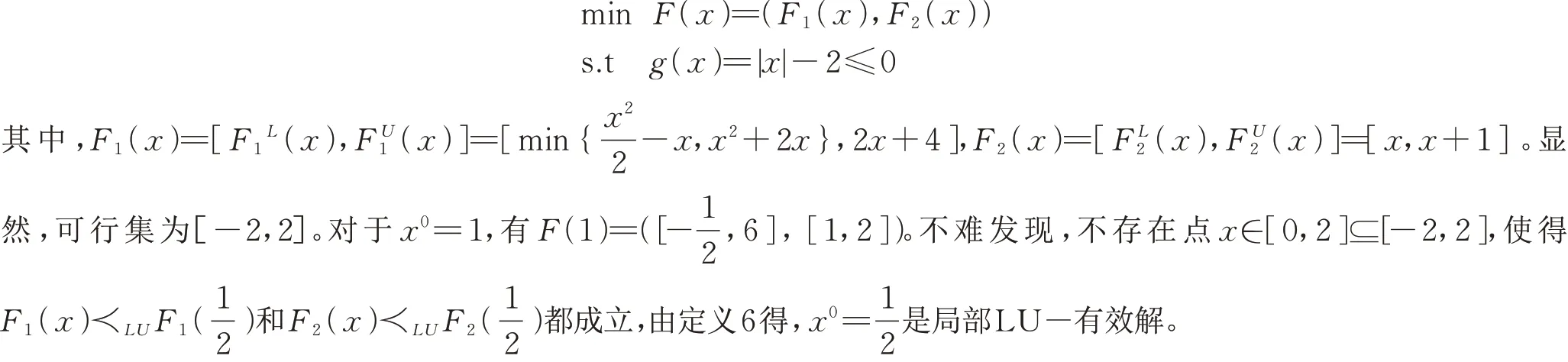
类似文献[8]命题2.14的证明,容易得到如下引理。
引理4 设x0∈Ω是问题(MIVOP)的局部弱LU-有效解当且仅当x0是如下多目标优化问题的局部弱Pareto-有效解:

其中Ω1:={ x∈Rngi(x)≤0,i∈P;hj(x)=0,j∈Q,FUℓ(x)≤FUℓ(x0),ℓ∈M }。
下面我们先给出(MIVOP)在广义Jacobi矩阵下的局部弱LU-有效解的Fritz-John必要条件。
定理1(Fritz-John必要条件) 设x0∈Ω 是问题(MIVOP)的局部弱LU-有效解,则存在乘子,λL∈Rm,λU∈Rm,μ∈Rp和τ∈Rq使得

证明:由引理4知,x0是(VOP)的局部弱Pareto-有效解。因此存在实数δ>0使得x0是如下优化问题唯一的弱Pareto-有效解

考虑如下优化问题:

因此。存在c>0使得对充分大k∈K有

所以

故对充分大的k∈K,有

这使得

由xk的定义和引理2得,0∈∂Φk(xk)。由引理3(iii)可得,

定义φ3:Rn→R为
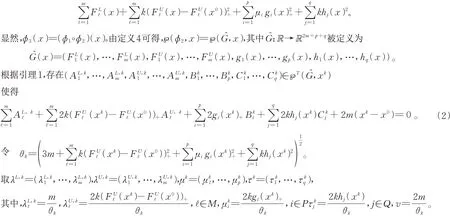
因此,式子(2)变为
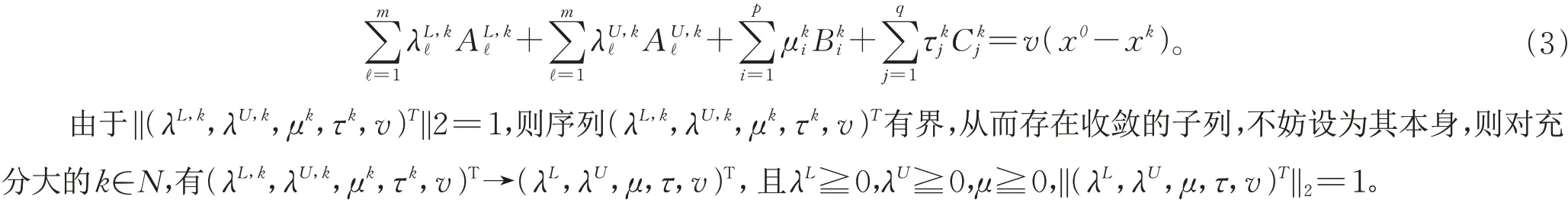
由广义Jacobi矩阵的局部有界性和上半连续性知,对充分大的k∈N有,
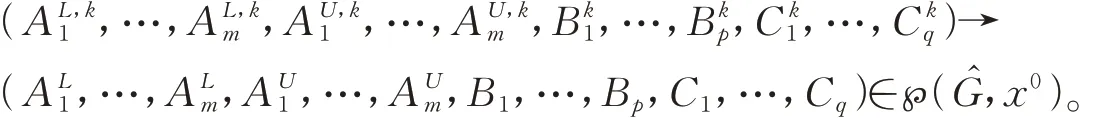
因此,对充分大的k∈N有,式子(3)可变为
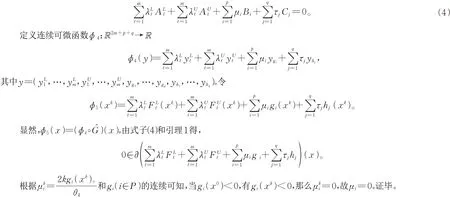
注2:在问题(MIVOP)中,当m=1和FL1=FU1,问题(MIVOP)退化为一般的单值优化问题,因此定理1是文献[10]定理3.1的推广。
下面例子说明定理1。
例2 设x∈R2,考虑如下问题:

则有
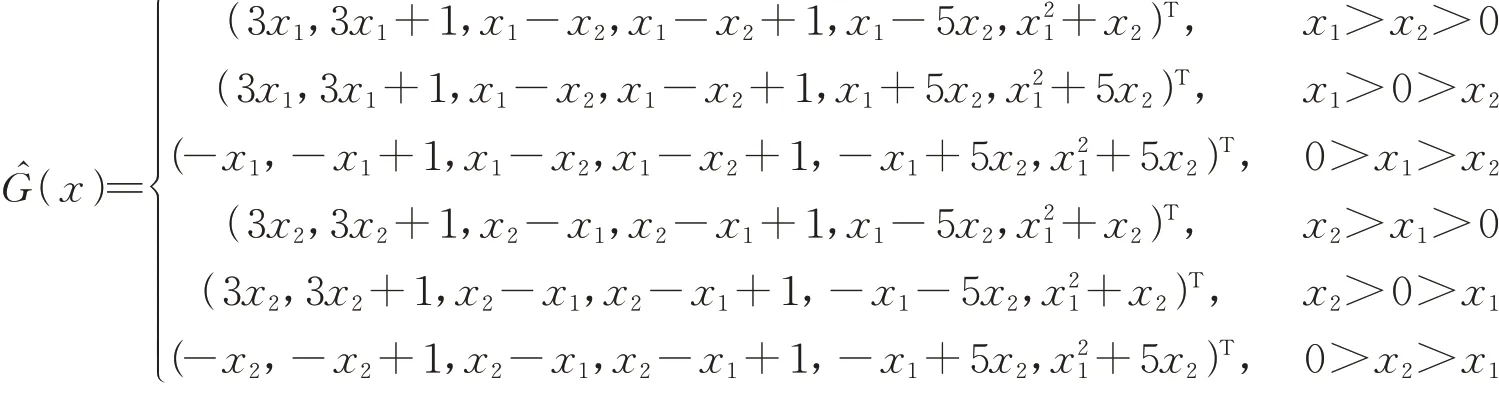
和

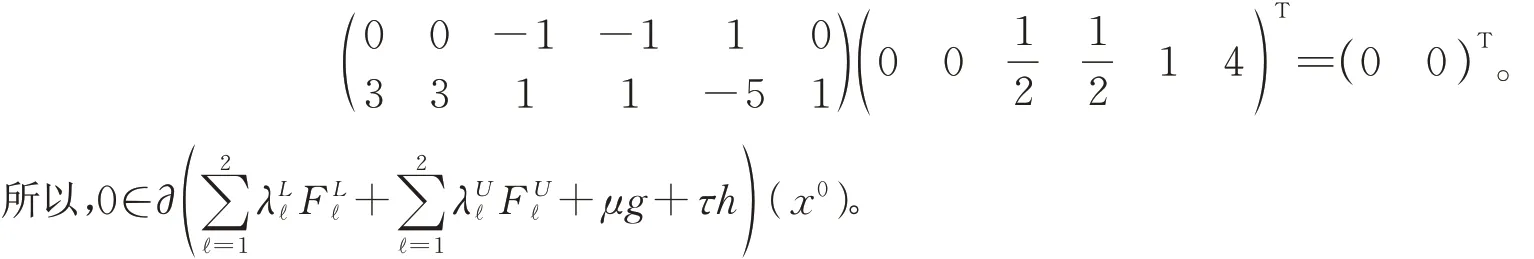
人们致力寻找模型(MIVOP)的局部弱LU-有效解的必要性条件。最近Antczak[8]在广义Salter约束规范条件下研究(MIVOP)的弱LU-有效解的必要条件。注意到,当广义Salter约束规范不成立时,文[8]的定理2.16将无能为力。以下例3说明这一点。易知,例3模型中的函数g是非凸的,故不满足广义Salter约束规范,从而文[8]的定理2.16无法使用。
为了建立(MIVOP)的局部弱LU-有效解的KKT必要条件,引入如下广义Mangasarian-Fromovitz约束规范(简记GMFCQ)。
定义7[13]称GMFCQ在点x0∈Ω成立,如果下列成立:
(i)对所有的矩阵(…,Bi,…,C1,…,Cq)∈℘T(G,x0),存在向量d∈Rn使得 Bi,d <0,(i∈I(x0))和 Aj,d =0( j∈Q),其中G=(…,gi,…,h1,…,hq)(i∈I(x0));
(ii)℘(H,x0)行满秩,即任意的矩阵C∈℘(H,x0)都是行满秩,其中H=(h1,…,hq)。
注3:下面例子3将给出满足GMFCQ的例子,我们之处并非所有的等式和不等式约束都能满足GMFCQ,如上述的例2的约束函数不满足GMFCQ。事实上,由
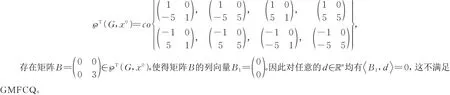
定理2(KKT必要条件) 设x0∈Ω是问题(MIVOP)的局部弱LU-有效解,并且约束函数在x0处满足GMFCQ,则存在λL∈Rm,λU∈Rm,μ∈Rp和τ∈Rq使得
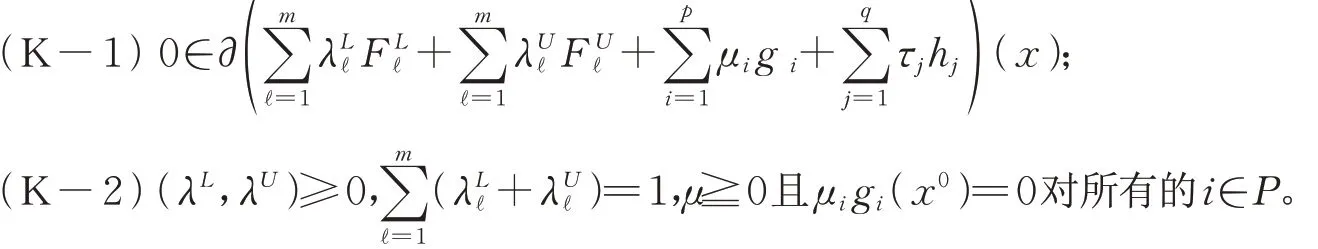
证明:由假设知,x0是问题(MIVOP)的局部LU-有效解,根据定理1,存在λ^L∈RmRm,λ^U∈Rm,μ^ ∈Rm和τ^∈Rm使得(FJ-1)-(FJ-3)成立。故存在矩阵
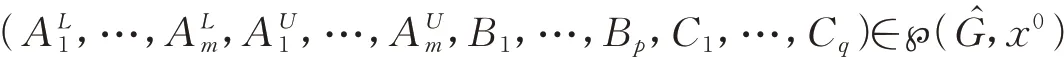
使得


注4:(i)在问题(MIVOP)中,当m=1和FL1=FU1,问题(MIVOP)退化为一般的单值优化问题,因此定理1是文献[10]定理4.2的推广。
(ii)为了比较定理1和定理2,我们把满足(FJ-1)-(FJ-3)和满足(K-1)-(K-2)的点x0分别称为FJ点和KKT点。容易证明,KKT点集包含于FJ点集,因此模型(MIVOP)满足GMFCQ的条件下,KKT条件必优于Fritz-John必要条件。
例3 设x∈R3,考虑如下问题:
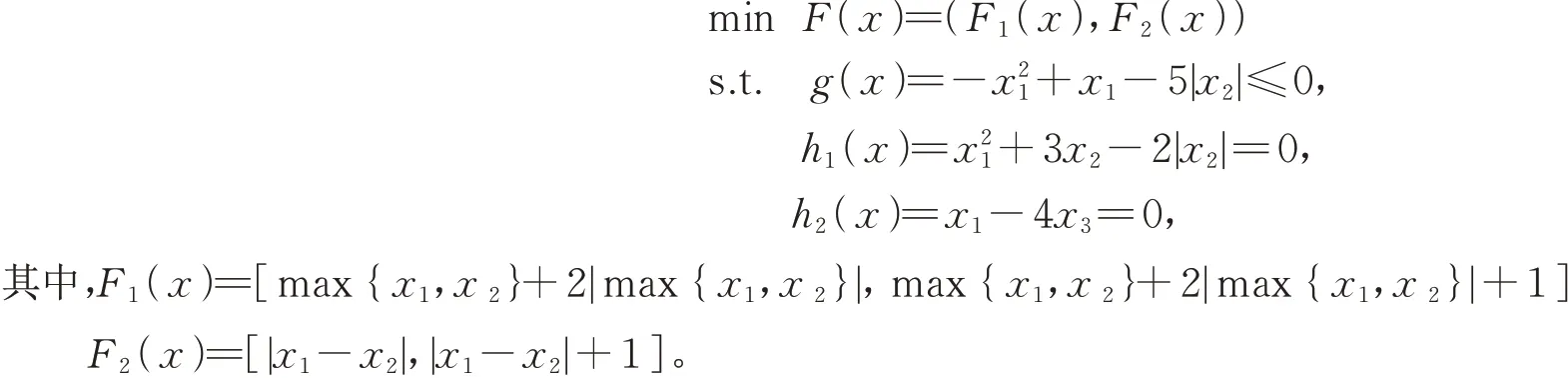
显然,x0=(0,0)T的弱LU-有效解。令
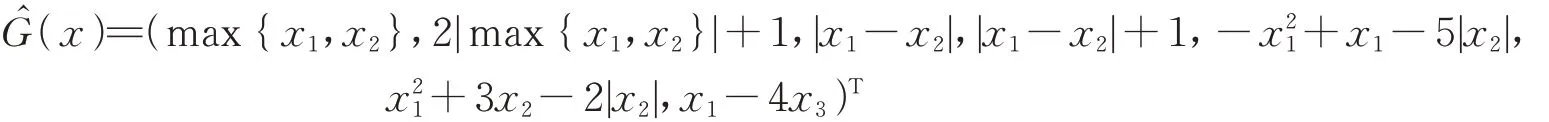
则
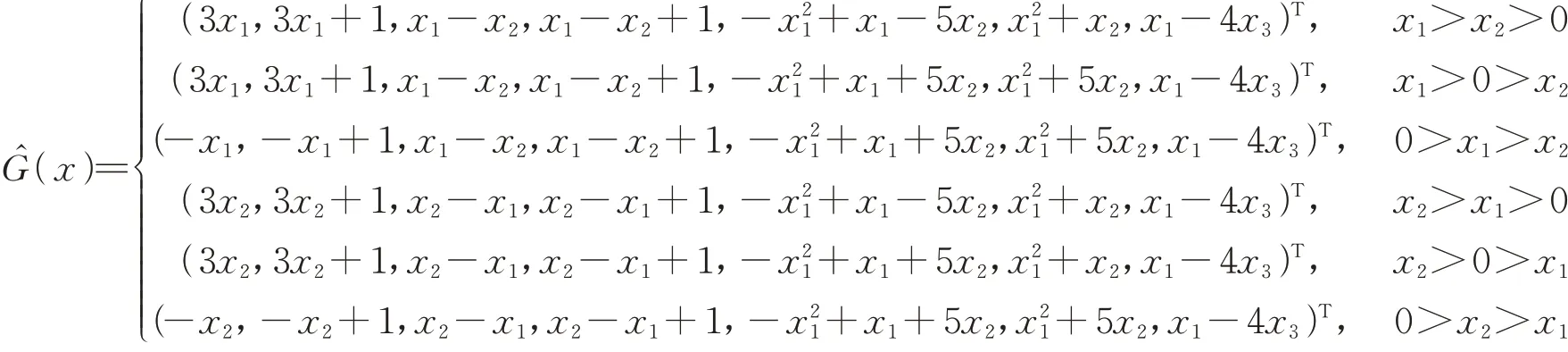
和

对任意矩阵B∈℘T(G,x0),存在α1,α2∈[0,1]且α1+α2=1使得,
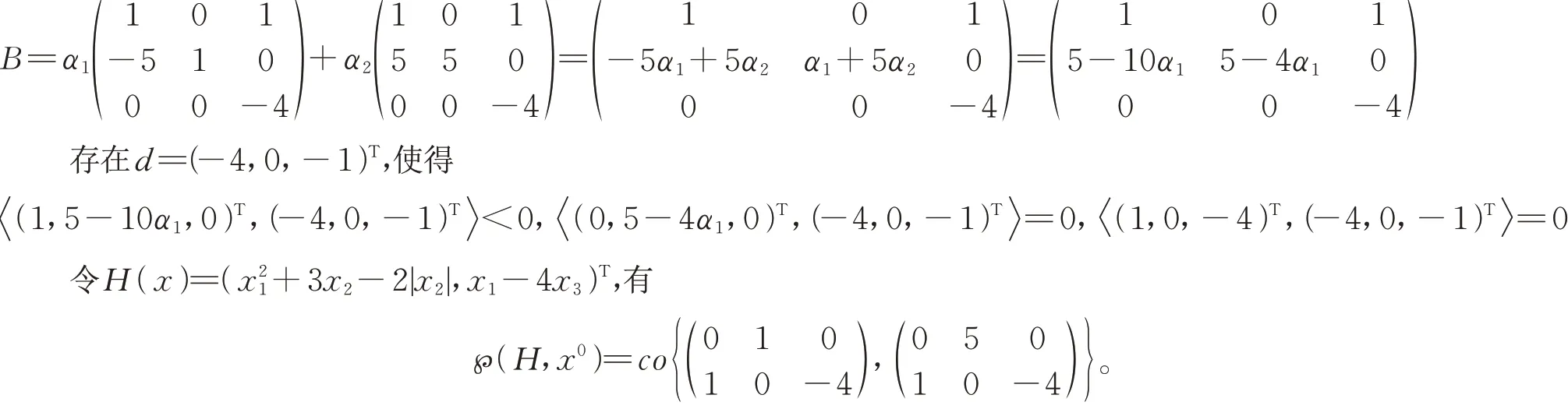
对任意矩阵C∈℘(H,x0),存在α1,α2∈[0,1]且α1+α2=1使得,
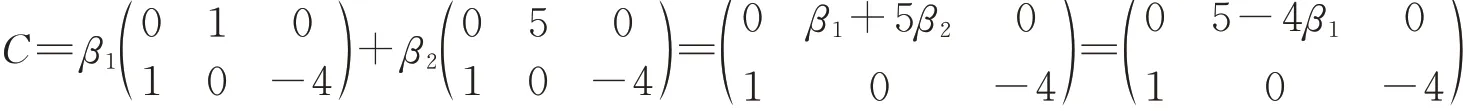
显然C是行满秩。由C的任意性,℘(H,x0)是行满秩。根据以上讨论,约束函数满足GMFCQ。取