指数、对数不等式问题“同构”处理策略

胡 振 刘 勇

(山东省淄博市临淄中学)

既含有指数函数又含有对数函数的不等式证明或不等式恒成立问题,是近年高考的常考题型,且大多以解答压轴题的形式出现.此类问题虽然综合性强、题型多变,但并非无规律可循,下面引例探究.

例1(2020 年新高考Ⅰ卷21)已知函数f(x)＝aex－1－lnx＋lna.

(1)当a＝e时,求曲线y＝f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

本题是含参的不等式恒成立问题,常用的方法是分离参数求函数的最值,但函数f(x)中既含有指数式,又含有对数式,因此本文给出其中一种通用的解题方法,即针对指数式的指数或对数式的真数进行相应变换,构造函数,再利用函数的单调性判断.

1 知识储备

转化、构造是应用同构法解题的关键步骤,常用的转化关系如下.

另外,还要熟悉上述转化关系式中等号左边函数的图像和性质,如f(x)＝xex.除此之外,f(x)＝,f(x)＝x±ex都是常考的函数模型.

2 知识拓展

我们可以进一步将上面的知识进行拓展,即通过转化建立不同函数之间的关联.例如,设f(x)＝xex,g(x)＝xlnx,则对函数g(x)进行转化可得g(x)＝xlnx＝elnxlnx＝f(lnx).

此外,还要注意积累一些重要的不等式,如切线不等式ex≥x＋1,其中直线y＝x＋1是曲线y＝ex在点(0,1)处的切线.

将不等式ex≥x＋1中的x换为lnx,可得x≥lnx＋1,即x－1≥lnx,其中y＝x－1是曲线y＝lnx在点(0,1)处切线.其他的变化形式还有如下几种.

求解有关问题时利用这些不等式进行放缩,可收到事半功倍之效.当然这些不等式只是我们推导得出的结论,在应用前要先进行证明.

3 策略应用

下面先来看例1第(2)问的解答.

方法1不等式f(x)≥1,即aex－1－lnx＋lna≥1,可按如下几个步骤构造同构函数:

1)将指数与对数分离,即分别放在不等号的两边,即aex－1≥lnx－lna＋1.

2)将aex－1化为同底数的指数函数,即

3)在不等号的两边同时加lna＋x－1,得

化简整理得

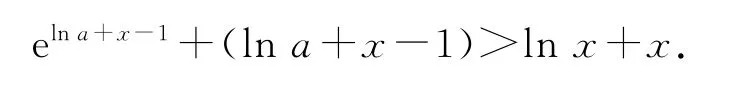
4)将不等号右边的x转化为elnx,即

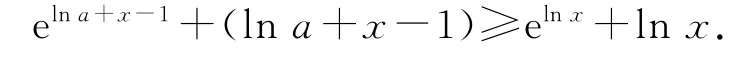
进而构造同构函数g(x)＝ex＋x,则将不等式elna＋x－1＋(lna＋x－1)≥elnx＋lnx转化为不等式g(lna＋x－1)≥g(lnx),再利用g(x)的单调性进行判断.

易证g(x)为增函数,所以只需lna＋x－1≥lnx,即lnx－x＋1≤lna.

令h(x)＝lnx－x＋1,求导得,由h′(x)＝0,得x＝1.在(0,1)上,h′(x)＞0,h(x)单调递增;在(1,＋∞)上,h′(x)＜0,h(x)单调递减,所以hmax(x)＝h(1)＝0,所以lna≥0,a≥1.

综上,a的取值范围是[1,＋∞).

当然也可以利用如下的构造方法.

方法21)将指数与对数分离,即分别放在不等号的两边,即aex－1≥lnx－lna＋1.

2)将不等号右边的对数式与常数合并得aex－1≥

3)在不等号的两边同时乘ex,再同时除以a,得

4)构造同构函数g(x)＝xex,易知此函数在(0,＋∞)上单调递增,故不等式可转化为

4 方法巩固

下面给出几道例题,深入体会这种解题方法的应用,题目条件略有变化,求解时要注意转化的方向及变形的方法.

例2对于任意x＞0,不等式2ae2x－lnx＋lna≥0恒成立,则实数a的最小值为_________.

方法1由条件可知a＞0,2ae2x－lnx＋lna≥0,可从如下几个步骤对不等式进行同构变形.

1)将指数式与对数式分别置于不等式的两边可得2ae2x≥lnx－lna.

2)不等号的右边同底数的两个对数之差可合并为同一对数,即

3)在不等式的两边同时乘x,再同时除以a,得

方法21)将指数式与对数式分别置于不等式的两边得2ae2x≥lnx－lna.

2)对不等号的左边进行变形得

3)在不等式的两边同时加2x＋lna＋ln2,得

化简得e2x＋lna＋ln2＋2x＋lna＋ln2≥ln2x＋2x.

4)再将不等号右边的2x进行指数化得

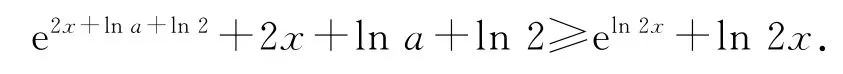
5)构造同构函数g(x)＝ex＋x,从而不等式e2x＋lna＋ln2＋2x＋lna＋ln2≥eln2x＋ln2x等价于g(2x＋lna＋ln2)≥g(ln2x),而函数g(x)＝ex＋x在(0,＋∞)上单调递增,所以2x＋lna＋ln2≥ln2x,即lna≥lnx－2x.以下同方法1.

(完)